强引力场中的自旋粒子的动力学特征

杨树政

(西华师范大学 物理与空间科学学院,四川 南充　637009)

强引力场中的自旋粒子的动力学特征

杨树政

(西华师范大学 物理与空间科学学院,四川 南充637009)

摘要：从描述自旋为1/2费米子动力学的Dirac方程和自旋3/2的费米子动力学的Rarita-Schwinger方程开始,推导出了静态球对称强引力场和稳态轴对称强引力场背景下的Hamilton-Jacobi方程,并利用Hamilton-Jacobi方程来研究了荷电球对称黑洞的量子隧穿行为。结论显示,Hamilton-Jacobi方程有助于人们更进一步的理解黑洞的热力学性质及其黑洞辐射特征。

关键词：强引力场；自旋粒子；动力学方程

0引言

Einstein广义相对论于1915年发表至今已有一百余年的历史[1-2]。一百余年以来,特别是近些年来,天体物理学家和理论物理学家在对天文学、天体物理学和理论物理学的前沿热点课题进行创新性研究的过程中,取得了一定的研究成果。人们在对黑洞物理理论的研究过程中,研究了各类黑洞的量子辐射特征,还对霍金辐射的理想模型进行了修正,同时也对各类黑洞的量子隧穿特征进行了有效的研究,得到了一系列有意义的结论；对黑洞熵、黑洞信息丢失疑难等热点课题进行了深入的讨论,丰富了黑洞热力学的内容[3-11]。在理论研究方面,中国学者不仅在理论上对黑洞物理的前沿热点问题开展深入的探索研究,而且得到Einstein场方程的新解,这个新解也得到了国内外同行专家认可和高度评价[12]。由于理论的不断发展,极大的激发了人们对宇宙、黑洞、引力波、暗物质、暗能量等前沿热点课题的观测及理论研究[13-17]。在天文观测方面,美国加利福利亚大学伯克利分校的科学家在后发星系团中发现了一个质量相当于210亿个太阳质量的超级大黑洞[18],接着,这个研究团队又在距离地球2亿光年的NGC1600星系中发现了一个质量相当于170亿个太阳质量的黑洞[19]。该星系与后发星系团相对,这两个大质量黑洞的发现意味着宇宙中还有一些大质量黑洞存在。此外, 北京大学吴学兵等人近年来也发现了一个相当于120亿个太阳质量的黑洞[20],相关理论研究和天文观测还在继续。在2015年,美国科学家利用LIGO(激光干涉引力波天文台)探测器首次探测到了13亿光年之外两颗初始质量分别为36倍和29倍太阳质量的黑洞合并时产生的引力波,这一重要的观测再次说明了广义相对论研究的重要意义[21]。超大质量黑洞的研究、超高速星的研究、超引力理论的研究等相关前沿热点课题都引起了天文学家和物理学家的广泛关注[22-29]。

本文是对强引力场中的自旋粒子的动力学特征进行研究。强引力场是指黑洞弯曲时空中的引力场,在弯曲的黑洞时空中,人们对各类黑洞的量子热效应和非热机制进行了一系列的研究,通过对霍金辐射的修正,用量子隧穿方法对静态、稳态和动态黑洞的研究取得了成功。在本文的研究过程中，将从描述自旋为1/2费米子动力学的Dirac方程和描述自旋为3/2的费米子动力学的Rarita-Schwinger方程出发,推导出球对称强引力场和轴对称强引力场背景下的自旋费米子动力学方程,并用这个方程来研究黑洞的量子隧穿辐射特征。

1Hamilton-Jacobi方程与自旋费米子动力学方程

一个球对称黑洞的时空度规可以用Schwarzschild线元表示为

(1)

对于自旋为3/2费米子,其动力学方程用Rarita-Schwinger方程来描述,在(1)式所示的弯曲时空中,粒子的动力学方程为

γμDμΨv+(m/ћ)Ψv=0,

(2)

γμΨv=0,

(3)

其中m是粒子的质量。自旋为3/2费米子的每一个波函数都由(2)和(3)式决定,在半经典情况下,用方程(2)即可描述自旋费米子的动力学行为[25]。而对于自旋为1/2费米子,可以用Dirac方程来描述其在弯曲时空中的动力学行为,即

γμDμΨ+(m/ћ)Ψ=0,

(4)

在方程(2)、(3)和(4)中

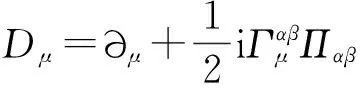
(5)

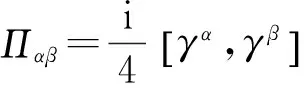
(6)

gamma矩阵必须满足弯曲时空中的反对易关系

(7)

这里gμν是(1)式所对应的时空的逆变度规张量。在线元(1)所表示的强引力场背景下,可以把gamma矩阵构建为[26]

(8)

上式中I表示为单位矩阵而Pauli矩阵σn分别表示为

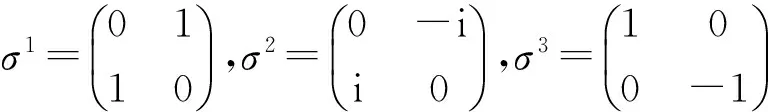
(9)

对于方程(2),可以令

(10)

上式中的系数为ξ=(AB)TM,其中A=(avcv)TM和B=(bvdv)TM且av，bv，cv，dv分别表示相应的矩阵,S为自旋费米子半经典的作用量。如果考虑Dirac方程的情况,则有

(11)

其中的A和B表示2×1的列矩阵。由(2)、(8)、(9)和(10)式,并利用半经典近似将含有因子ћ的项略去,这样就可以得到一个矩阵方程

(12)

其中

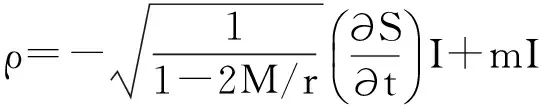
(13)

(14)

(15)

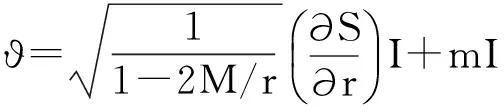
(16)

求解方程(12),可以得到

(ε-ϑζ-1ρ)A=0，(ϑ-εζ-1ρ)B=0，

(17)

显然,如果要求上两式子有非平凡解,则 (17)和(18)式中的系数项必须等于零。基于ζρ=ζρ,可以得到

det(εζ-ϑρ)=0，

(18)

(19)

很明显,此方程就是描述时空背景(1)中自旋费米子的动力学方程,相当于Schwarzschild黑洞时空中的Hamilton-Jacobi方程gμv(∂S/∂xμ)(∂S/∂xv)+m2=0。

对于带有电荷的Reissner-Nordström黑洞，其线元可以表示为

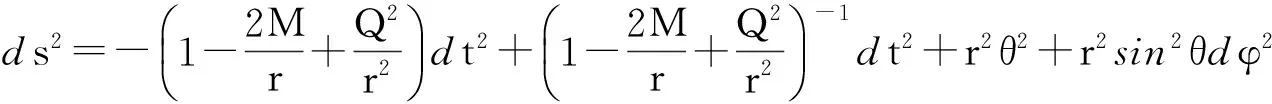
(20)

(21)

Pauli矩阵σn如(9)式所示。由gamma矩阵 (21)及(10)和(11)式,考虑到自旋3/2的费米子及自旋1/2的费米子,都可以得到

(22)

其中

(23)

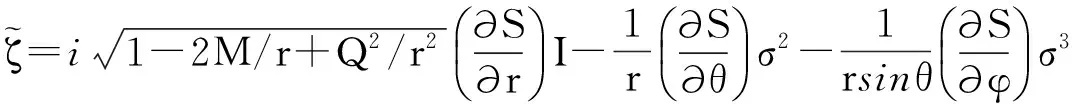
(24)

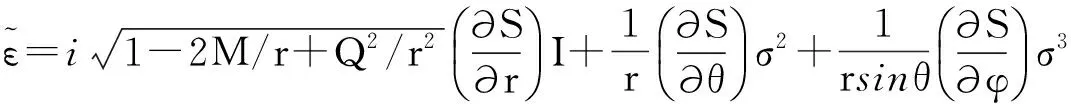
(25)

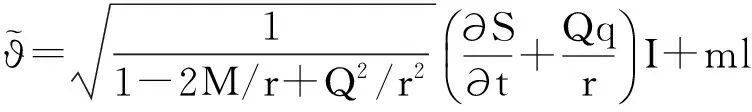
(26)

根据非平凡解的条件,可以得出

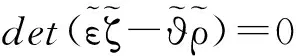
(27)

利用Pauli矩阵的反对易关系,把(23)、(24)、(25)和(26)式代入方程(27)中,得到

(28)

这个方程与gμv(∂S/∂xμ+qAμ)(∂S/∂xv+qAv)+m2=0一致。这是(20)式所表示的弯曲时空中的质量为m,电荷为q的粒子的Hamilton-Jacobi方程。

对于稳态轴对称强引力场,其一般形式的时空线元表示为

ds2=gttdt2+grrdt2+gθθdθ2+2gφtdtdφ+gφφdφ2。

(29)

对于上述线元的时空背景，gamma可以构建为

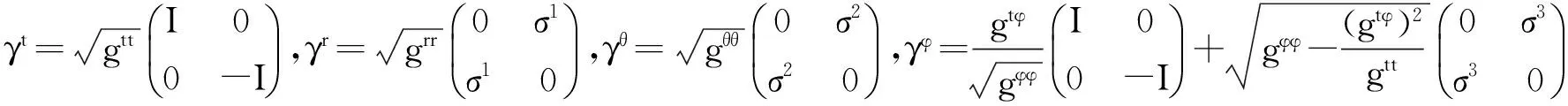
(30)

Pauli矩阵如(9)式所示。通过计算可得矩阵方程

(31)

其中

(32)

(33)

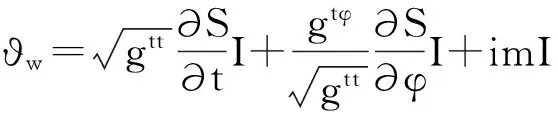
(34)

由于ρwζw=ζwρw,如果要得到非平凡解,则必须有det(εwζw-ϑwρw)=0,考虑到Pauli矩阵的反对易关系,就可以得到轴对称稳定黑洞时空背景中的Hamilton-Jacobi方程为

(35)

至此,已经从描述自旋为1/2费米子在弯曲时空中的Dirac方程和描述自旋为3/2费米子在弯曲时空中运动的Rarita-Schwinger方程中都推导出了Hamilton-Jacobi方程。从以上讨论中可以看出,Hamilton-Jacobi方程是一个非常基本的半经典的粒子运动方程,运用这个方程人们可以统一的描述各种自旋粒子的动力学行为[27]。知道了Hamilton-Jacobi方程,可以对黑洞的量子隧穿及量子热效应机制进行研究。以下是对Reissner-Nordström黑洞的隧穿辐射的研究。

2Hamilton-Jacobi方程与黑洞的量子隧穿辐射

以荷电的球对称黑洞为例来介绍Hamilton-Jacobi方程在量子隧穿理论中的应用。在之前的讨论中,Hamilton-Jacobi方程可以用来研究任意自旋粒子的隧穿辐射,因此,计算球对称荷电黑洞时空中的费米子的隧穿辐射时，只需要考虑(28)式，并将作用量S分解成

S=-ωt+R(r)+Θ(θ,φ)，

(36)

其中ω是隧穿粒子的能量,所以,将方程分离变量可得

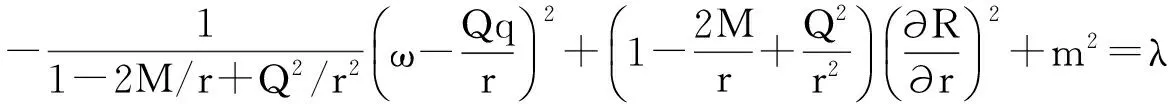
(37)

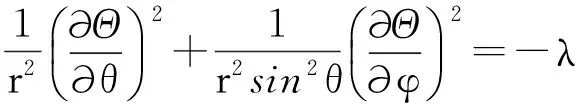
(38)

方程(37)代表辐射粒子的径向运动方程,方程(38)属于Hamilton-Jacobi方程中的角向部分,λ是一个常数。对于荷电的球对称黑洞,其隧穿行为与径向部分有关,所以,由方程(37)式可以得到

(39)

在事件视界面上,径向作用量为

(40)

上式中,+(-)代表出(入)射解,ω0=Qq/r+,由于黑洞隧穿辐射只与虚部有关,因此,实部Ξ(Realpart)可以不考虑。在黑洞事件视界面上,辐射粒子的隧穿率为

(41)

对比Boltzmann因子表达式,可得[28]

(42)

(42)式就是荷电的球对称黑洞的Hawking温度。当Q=0时,(42)式就退回到Schwarzschild黑洞的Hawking温度。可以看出,在半经典情况下,黑洞的温度只与自身的性质有关,黑洞质量的大小将对黑洞的辐射性质产生影响。近几年来,通过对量子引力的研究,人们发现在Hawking隧穿辐射中引入量子引力理论,如广义不确定性原理和彩虹引力,可以修正之前得到的半经典结论,所得到的结果不仅与黑洞自身的性质有关还与其辐射粒子的性质相关。这些修正很好的解决了黑洞信息丢失等难点问题,因此受到了人们的广泛关注,这也成为现在黑洞物理发展的一个重要方面。

3结论

从自旋为1/2费米子的Dirac方程和自旋3/2费米子的Rarita-Schwinger方程出发,都得到了Hamilton-Jacobi方程,并利用该方程研究了荷电的球对称黑洞时空中的费米子隧穿率和黑洞的Hawking温度。根据研究结论，Hamilton-Jacobi方程可以由任意自旋粒子动力学方程推导出来,这说明Hamilton-Jacobi方程是一个基本的半经典方程,可以使用这个方程来研究任意自旋粒子的量子隧穿行为。同时,通过对比之前的工作,可以明显的看出,使用Hamilton-Jacobi方程来研究黑洞的隧穿辐射是有效的方法,尤其是费米子隧穿,由于不需要再构建复杂的gamma矩阵进行复杂运算,这就更有利于人们开展深入的创新性研究。

参考文献：

[1]赵峥.黑洞与弯曲的时空[M].山西:山西科学技术出版社,2000:1-10.

[2]赵峥.黑洞的热性质与时空奇异性[M].北京:北京师范大学出版社,1999:2-25.

[3]HAWKINGSW.Particlecreationbyblackholes[J].Commun.Math.Phys.,1976,43:199-22.

[4]KRAUSP,WILCZEKF.Self-interactioncorrectiontoblackholeradiance[J].Nucl.Phys.B,1995,433:403-420.

[5]KERNERR,MANNRB.Tunnelling,temperature,andTaub-NUTblackholes[J].Phys.Rev.D,2006,73:104010.

[6]WUSQ,JIANGQQ.RemarksonHawkingradiationastunnelingfromtheBTZblackholes[J].JHEP,2006,3:79.

[7]BANERJEER,MAJHIBR.Quantumtunnelingandbackreaction[J].Phys.Lett.B,2008,662:62-65.

[8]杨树政,李慧玲,蒋青权,等.稳态轴对称黑洞量子隧穿特征及辐射谱的研究[J].中国科学:物理学 力学 天文学,2007,37(1):66-75.

[9]CHEND,YANGSZ.HawkingradiationoftheVaidyaBonnerdeSitterblackhole[J].NewJ.Phys.,2007,9:252.

[10]LINK,YANGSZ.FermionstunnellingofanewformFinslerianblackhole[J].Chin.Phys.Lett.,2009,26:010401.

[11]LINK,YANGSZ.Fermionstunnelingfromthehigher-dimensionalblackhole[J].Phys.Rev.D,2009,79:064035.

[12]WUSQ.GeneralnonextremalrotatingchargedAdSblackholesinfive-dimensionalU(1)3gaugedsupergravity:asimpleconstructionmethod[J].Phys.Lett.B,2012:707,286-291.

[13]FENGZW,LIGP,ZUXT.QuasinormalModesofMasslessScalarFieldPerturbationinReissner-Nordstrom-deSitterQuintessenceSpacetime[J].Int.J.Theor.Phys.,2016,55:367-379.

[14]冯中文,罗夏. 超高速星的搜寻与研究 [J].西华师范大学学报(自然科学版),2014,35(1):68-73.

[15]FENGZW,LIHL,ZuXT,etal.QuantumcorrectionstothethermodynamicsofSchwarzschild-Tangherliniblackholeandthegeneralizeduncertaintyprinciple[J].Eur.Phys.J.C,2016,76:212.

[16]LIGP,CAOB,FENGZW,etal.StronggravitationallensinginaBrane-worldblackhole[J].Int.J.Theor.Phys.,2015,54:3103-3114.

[17]CHOIKY,GONGJO,SHINCS.WIMPisocurvatureperturbationandsmallscalestructure[J].Phys.Rev.Lett.,2015,115:211302.

[18]MCCONNELLNJ,MACP,GEBHARDTK，etal.Twoten-billion-solar-massblackholesatthecentresofgiantellipticalgalaxies[J].Nature,2011,480(7376):215-218.

[19]THOMASJ,MACP，MCCONNELLNJ，etal.A17-billion-solar-massblackholeinagroupgalaxywithadiffusecore[J].Nature,2016,532,340-342.

[20]WUXB,WANGF，FANX，etal.Anultra-luminousquasarwithatwelve-billion-solar-massblackholeatredshift6.30[J].Nature,2015,518(7540):512-515.

[21]ABBOTTBP,ABBOTTR，ABBOTTTD，etal.Observationofgravitationalwavesfromabinaryblackholemerger[J].Phys.Rev.Lett.,2016,116(6):061102.

[22]HILLSJG．Hyper-velocityandtidalstarsfrombinariesdisruptedbyamassivegalacticblackhole[J]．Nature,1988,331(6158):687-689．

[23]ZHENGZ，CARLINJL，BEERSTC,etal.ThefirsthypervelocitystarfromtheLAMOSTsurvey[J].Astrophys.J.Lett.,2014,785(2):23.

[24]IBEM,KITANOR.Gaugemediationinsupergravityandgravitinodarkmatter[J].Phys.Rev.D,2007,75(5)：349-354.

[25]LINK,YANGSZ.Fermionstunnelingfromthehigher-dimensionalblackhole[J].Phys.Rev.D,2009,79(6):064035

[26]LINK,YANGSZ.Fermionstunnelingofhigher-dimensionalkerranti-de-sitterblackholewithonerotationalparameter[J].Phys.Lett.B,2009,674(2):127-130.

[27]杨树政,林恺.Hamilton-Jacobi方程和来自Kerr-TAUB-NUT黑洞的隧穿辐射[J].中国科学:物理学 力学 天文学,2010,40(4):507-512.

[28]JIANGQQ.Diracparticletunnelingfromblackrings[J].Phys.Rev.D,2008,78(4):044009.

[29]吴迪，吴双清，杨树政.ω-变形Kaluza-Klein超引力的转动双荷黑洞解及其热力学[J].科学通报：2015，60(34)：3345-3348.

DynamicsEquationofSpinParticlesinaStrongGravitationalField

YANGShuzheng

(CollegeofPhysicsandSpaceScience,ChinaWestNormalUniversity,NanchongSichuan637009,China)

Abstract:The Hamilton-Jacobi equation is a kind of semi-classical equation,which plays an important role in black hole physics. In this paper,due to the Dirac equation which descripts the dynamics of fermion with spin 1/2 and the Rarita-Schwinger which descripts the dynamics of fermion with spin 3/2,we derived the Hamilton-Jacobi,and use it to investigate the tunneling from a charged spherical symmetric black hole.Our discussion shows that the Hamilton-Jacobi can greatly simplify the research.Therefore,the Hamilton-Jacobi is helpful for people to know more about the thermodynamic properties of black holes.

Keywords：strong gravitational field；spin particles；dynamics equation

文章编号：1673-5072(2016)02-0125-06

收稿日期：2016-05-10

基金项目：国家自然科学基金项目(11573022)

作者简介：杨树政(1955—),四川雅安人, 博士，教授，博士生导师，主要从事广义相对论及黑洞物理研究。 通讯作者：杨树政，E-mail:szyangcwnu@126.com

中图分类号：O412.1

文献标志码：A

DOI：10.16246/j.issn.1673-5072.2016.02.001