物理问题表征态的构建与演化分析
2016-07-06秦笑春
秦笑春

摘 要:通过对物理学发展历史的分析,确立了问题表征态的内涵,从信息论的角度明确表征态具有确定性增加的演化特性。本文具体研究了从物理表征到数学表征的过程,明确了状态数学化、过程数学化和约束关系数学化三种途径能引导问题表征态向着确定度增大的方向演化。通过对实例的分析,进一步明确了这三种途径对于物理问题解决的价值。
关键词:问题表征态;确定性;约束关系;解题
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2016)6-0064-4
1 问题的提出背景
表征是信息在人头脑中的呈现方式,是客观事物的反映。问题表征则是问题所涉及的信息在人头脑中呈现出的形态。1978年,McDermott和Larkin提出了物理问题的4个表征步骤:文字表征、朴素表征、科学表征、数学表征。廖伯琴在此基础上提出了力学问题的表征体系,并用口语报告分析法做了研究[1]。而邓铸提出了表征态理论,指出表征态是一连续、非线性的变化过程,包含了6种不同层次的表征态[2]。邢红军结合协同论提出了自组织表征理论,它是一个连续与突变、独立与关联、控制与自发、协同与竞争、必然与偶然相结合的非线性过程,同时又呈现出了7种不同的表征层次[3]。此外,还有众多的研究者提出了自己的观点。
总体上,问题表征态具有动态性、连续性、非线性等复杂系统的特征,但目前只能用一些相对的稳态将整个动态过程割裂成几个不同的层次。如此一来,若能对表征态演化作更细致的表述,将给教师的教学以参考。同时,物理问题表征态的具体内涵有待确立。
2 问题表征态的内涵与演化
经典力学在时间与空间中研究物质运动的规律与结构特征,它经历了伽利略、开普勒、笛卡尔、惠更斯、牛顿等人的发展。在本体论承诺、数学化表征和发现型实验三大主题的交织下,一个具有自我修正、自我发展的知识结构体系逐渐形成了。本体论是指共享概念模型的形式化规范说明,本质上是对基本模型、基本概念的构建。数学化表征是指用数学语言来表征物理实在、表征自然界的客观规律,以方便脱离物理实在进行逻辑推理,避免了生活经验对问题解决的负面影响。而发现型实验是通过操控手段来探究自然规律,能对新理论进行实验验证,也能帮助研究者发现新的物理规律。
问题表征态的内涵应该在物理学的发展过程中寻找,和物理学保持一致。物理学研究的是物质运动规律,因此问题表征态是围绕“物质运动”这一主题而形成的一个具有范畴性的体系。从本体论看,表征态由一些基本概念构成,例如力学中的表征态包含质量m、位移x、时间t,以及力F、速度v、加速度a等。从数学化表征上看,表征态也必须呈现物理量间的数学关系,如在力学中常见的是函数关系。因此,问题表征态的内涵包含了物理量和它们间的数学关系。
表征态的演化是人类对未知新事物追求认知平衡而发生的改变,它源于人类物理现象与过程的认知需要。从信息论的角度看,问题表征态是从不确定到确定、从不完备到完备的方向演化。表征终态与初态有很大的不同,它所包含的信息量更多、确定性程度更高,因此在态的演化过程中必然包含着“确定性信息”的引入。在物理问题中,该“确定性信息”是物理规律、物理法则等,它存在于问题解决者的头脑中,蕴藏于表征的最终状态中,但不存在于表征的初始状态。那么,对于“确定性信息”是如何引入到表征态并促使其朝终态演化的,表征态是如何同化与顺应物理规律、问题信息的,这是整个问题的关键所在。
3 物理表征的演化
文字表征、朴素表征和物理表征是解决原始问题的关键步骤,而物理表征和数学表征则是解决结构良好的习题所注重的内容。从文字表征到物理表征的过程也是建立物理模型、明确物理量的过程,它涉及定向表征、抽象表征、图像表征、赋值表征等多种表征层次,是原始问题所关注的内容之一。
从物理表征到数学表征的主要思维模式是演绎推理,该过程因此而变得有迹可循。既然表征态必然依据实际的物理过程,那么物理量间的关系建构就是物理规律或其他约束关系的数学化表征。而由于时间与空间是物理过程的主要参量,因此状态数学化、过程数学化以及约束数学化这三种有效的途径能将物理实在包含的信息以数学函数的形式在表征态中表征出来。
3.1 状态数学化
状态数学化是在某时刻利用某物理规律建立起表征态中物理量间的数学关系。高中物理知识体系中,最常见的是利用牛顿运动定律建立力学量和运动学量之间的关系,此时初始表征态中定有力学信息或运动学信息。例如,已知某个力的大小、恰好通过圆轨道的最高点、恰好脱离轨道、恰好发生相对滑动等力学量的信息,或者如匀加速运动、圆周运动等运动学量的信息。因此,可以在状态数学化的作用下引入牛顿定律,建立物理量间的关系f(Fx,m,xx)=0,该函数中Fx是指各种力,xx指的是各种运动学量,且涉及到的都是状态量,不显含时间t。
3.2 过程数学化
过程数学化是指在某段时间利用某物理规律,建立表征态中物理量间的数学关系。一种途径是从力在时间上的累积来分析,常见的是使用运动学结合牛顿定律来建立物理量间的数学关系f(Fx,m,xx,t)=0,且显含时间t,如平抛运动、匀变速直线运动等可建立位移-时间函数、速度-时间函数;另一种途径是从力在空间上的累积来分析,建立任意两个状态间物理量的数学关系f(Fx,m,xx,x)=0,且显含位移x,常见的是利用能量的转化与守恒思想,如动能定理、机械能守恒定律等来建立量之间的关系。
3.3 约束数学化
有时仅靠物理规律来建立函数关系并不能反映表征态所具有的全部关系,可能还存在着非物理的约束关系,如空间几何关系、时间关系、数量关系等。例如,在多体问题的数学表征中,常常存在着诸如多个物体间的位置关系等隐藏的关系,只要将约束关系用函数关系来表征即可解决。
4 实例展示
下面以几道计算题为例,阐述这三种途径对于物理问题解决的意义。
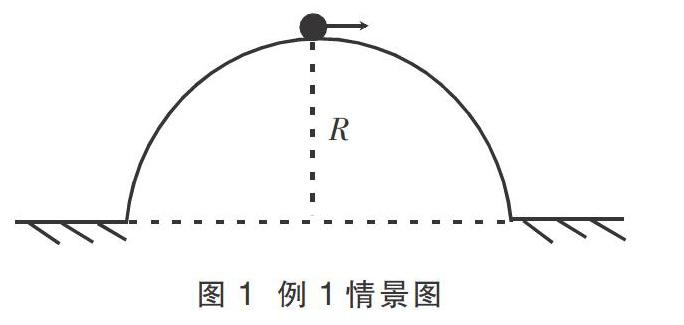
例1 一个光滑半圆球固定在水平面上(如图1),顶部有一个小物体原来处于静止状态,在某种扰动下它向右滑落,求物体飞离半圆球面时其位置与圆心的连线和竖直方向的夹角。
解析 在这个题目中虽然没有具体给出物理量,但还是能比较容易地构建出物理表征态f(m,N,g,r,θ),下面建立物理量之间的函数关系。该问题中小物体共有两段物理过程,一是沿半圆球的圆周运动,二是飞离半圆球后的抛体运动。小物体在圆周运动时受到了重力和弹力作用,而在做抛体运动时只受重力作用,因此该问题的临界状态是球与物体间的弹力为零的状态,即小物体飞离半圆球面时的状态。下面就可将过程与状态分别数学化,该题只求分离时所处位置同球心连线与竖直方向的夹角,因此只需将圆周运动过程数学化,用动能定理建立f1(R,θ,v)=0,再将特殊点的状态数学化,用牛顿第二定律建立f2(R,θ,v)=0,联立等式可求得答案cosθ=。
例2 如图2为一固定在竖直平面内的轨道。直轨道AB与光滑圆轨道BC相切,圆弧轨道的圆心角为37 °,半径r=0.25 m,C端水平,AB段的动摩擦因数为0.5。竖直墙壁CD的高H=0.2 m,紧靠墙壁在地面上固定一个和CD等高,底边长L=0.3 m的斜面。一质量m=0.1 kg的小物块(视为质点)在斜面轨道上从距离B点l=0.5 m处静止释放,后从C点水平抛出。取g=10 m/s2,sin37 °=0.6,cos37 °=0.8,求:
(1) 小物块运动到C点时对轨道压力的大小;
(2) 小物块从C点抛出至击中斜面的时间;
(3) 改变小物体释放的初始位置,求小物体击中斜面时动能的最小值。
解析 此问题的物理表征态是f(m,N,g,H,L,l,r,θ,μ)以及位置关系图,涉及到了9个物理量。这是一个单体多过程的问题,涉及到了两个过程和一个状态以及一个约束关系,下面只需要将它们分别数学化。第一问,由于物体状态在C点 ,重力与支持力作用下做圆周运动,可构建出f1(N,m,g,vc,r)=0的关系式。根据A到C的过程,利用动能定理,建立起f2(g,vc,l,r,θ,μ)=0的关系式,消去速度vc即可求得答案。第二问是平抛运动,将其数学化可获得f3(x,vc,t)=0和f4(y,g,t)=0,由于和一特定的斜面相碰,存在一约束方程即f5(x,y)=0,将这3个方程联立可求得答案。第三问根据动能定理获得方程f6(Ek,m,vc,y)=0,若要求最小值,则需要将vc或者y代换,根据f3、 f4、 f5函数,消去t和x即可获得关系式f7(vc ,y)=0,再联立f6=0,消去vc,即可求得最小动能。
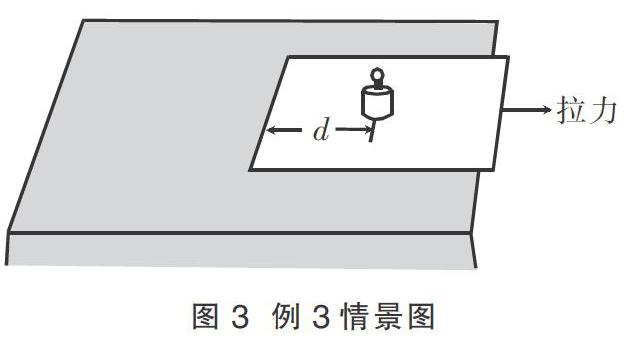
例3 如图3所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验。若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ,重力加速度为g。
(1)当纸板相对砝码运动时,求纸板所受摩擦力的大小;
(2)要使纸板相对砝码运动,求所需拉力的大小;
(3)本实验中,m1=0.5 kg,m2=0.1 kg,μ=0.2,砝码与纸板左端的距离d=0.1 m,取g=10 m/s2。若砝码移动的距离一旦超过l=0.002 m,人眼就能感知,为确保实验成功,纸板所需的拉力至少多大?
解析 对于整个问题而言,物理表征态是f(F,f,N,m1,m2,d,l,μ,g)以及一个图像,同时该问题涉及了纸板和砝码两个研究对象。第一问可以用隔离法分析物体的受力,考察的是受力分析能力,较为容易建立关系。第二问,砝码发生相对运动时力学量的要求是摩擦力达到了最大静摩擦力,依据此临界状态可列出f1(μ,g,a)=0的关系式,同时此状态下具有相同的加速度,利用整体法可列出f2(F,m1,m2,μ,g,a)=0的关系式。联立消去中间物理量a即求得答案。
对于第三问,首先分析两个研究对象各自的运动过程。若砝码在纸板对它的滑动摩擦力下做加速运动的时间为t1,掉下纸板后在桌面摩擦力作用下做减速运动的时间为t2,分析这两段运动的关系,发现t1=t2,根据整个运动过程建立f3(l,μ,g,t1,t2)=0的关系式。纸板在外力和摩擦力作用下一直做加速运动,由于运动的等时性,其运动时间为t1,位移为x,同样的可建立f4(F,m1,m2,x,μ,g,t1)=0的关系式。其次,再寻找两个研究对象间的联系。此时,运动的等时性和摩擦力的相互性已经在前面两个式子中体现出来了。而在空间上,由于两物体的相对运动的位移为d,因此还可以建立f5(l,d,x)=0的关系式。只要将这几组等式联列即可获得答案。
5 结束语
这3个例子展示了物理表征态的构建以及从物理表征到数学表征的演化过程,展示了状态、过程与约束数学化能促进学生问题解决表征态的发展,实现问题解决的目的。虽然它们是力学问题,但任何物理问题的解决都是在某种方式下将问题所涉及的核心规律从知识库中引入表征态中去,进而用数学关系来表征问题的物理特征,实现用已有的知识同化和顺应题中信息。另外,本文给出了从物理表征到数学表征相对具体的操作步骤,当然这三种途径也不可能完全展示表征态演化的每一个步骤,只是在前人的基础上使之更加具体而已。
参考文献:
[1]廖伯琴.中学力学问题表征体系的动态特征[J].心理学报,2001,33(3):51—54.
[2]邓铸.问题解决的表征态理论[J].心理学探新,2003(4):17—20.
[3]邢红军.自组织表征理论: 一种物理问题解决的新理论 [J].课程·教材·教法,2009,29(4):60—64.
(栏目编辑 邓 磊)
