直角三角形的分类在数学课堂教学的渗透

郑为勤

【摘要】直角三角形的分类有别于其他教学内容与方法，如何熟练掌握、准确应用，并非几课时的学习就能达成，必须经过一个循序渐进、不断提升的过程.针对学生在不同学习阶段拥有的知识和水平教学，使学生逐步掌握.

【关键词】分类；意识；渗透；方法

分类讨论是一种重要的数学思想方法，其中直角三角形的分类是近年各省市中考数学试卷中经常有的一个考点.如何在中学各个不同学段，通过专题归纳和训练，使学生掌握此类问题呢？本文以教学中所用的实例，对在课堂教学中如何渗透直角三角形分类思想进行研究.

一、树立意识，及时引入分类

数学思想方法的教与学具有“隐蔽性”，需要教师为学生有意搭建桥梁，及时渗透，学生才有机会认识“庐山真面目”.在讲授数学概念、公式、定理的形成过程中渗透分类思想方法，抓住新旧知识之间的联系，创设情境，让学生初步感悟直角三角形的分类.

例如：七年级下册第四章“认识三角形”的第2课时学生们认识了有一个角是直角的三角形叫做直角三角形，它的三条边有直角边、斜边之分.在学生学习了“勾股定理”教学阶段，我们可以设计以下题目让学生思考.

1.如果直角三角形的两直角边长分别为3，4，那么斜边长为.

2.如果直角三角形的两边长分别为3，4，那么第三边长为.

这两个题目通过学生练习，辨析什么情况下应该分类讨论，不仅很好的揭示了直角三角形概念的内涵，并从中发展了学生的抽象概括能力和逻辑思维能力.课堂教学以显性的数学知识“直角边”“斜边”为主线，而分类思想方法则隐藏在数学知识的背后，这样的概念教学让学生感受了分类的必要性，并完成了合理的正迁移.

二、看准时机，提高分类认识

需要分类思想解决的问题，如果分类标准不确定，极易造成思维过程中思考片面，致使解答不完整.教师创设问题情境，给学生独立思考、交流讨论的时间，再适时点拨，让学生顿悟.学生尝到甜头，体会了分类思想在解题时的优势，自然有了探索欲望，渗透分类思想也就水到渠成.

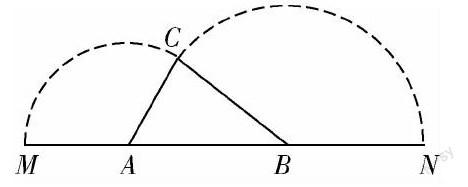
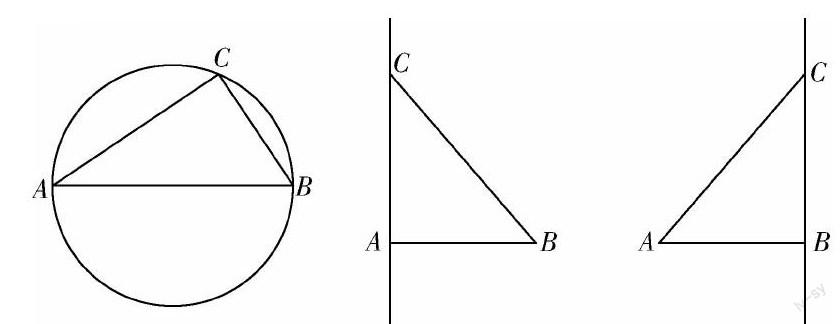
例 如图，已知A，B是线段MN上的两点，MN=4，MA=1，MB>1.以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M，N两点重合成一点C，构成△ABC，设AB=x.若△ABC为直角三角形，求x的值.

根据题意易分析得△ABC的各边长分别为：AB=x. AC=MA=1，BC=BN=3-x.解决这个问题应该分情况讨论，因为不知道在三角形中哪一个是作为斜边存在的.所以有三种情况，即：①若AC为斜边，则1=x2+（3-x）2，即x2-3x+4=0，无解.

②若AB为斜边，则x2=（3-x）2+1，解得x=53，满足1③若BC为斜边，则（3-x）2=1+x2，解得x=43，满足1