高职椭圆的标准方程教学的教学设计

陈忠东

【摘要】椭圆的教学抽象性较强，运算较繁琐，高职学生往往难以接受，本文采用新的思路，类比学生熟悉的圆的方程，提出椭圆方程的猜想，并对猜想的正确性进行验证，引导学生通过实验、类比、猜想等方法进行探索式学习，可在教学中达到理想的教学目标.

【关键词】椭圆；高职数学；教学设计

一、问题的提出

对于椭圆的标准方程教学，大都是教师以实例图片引起学生探究什么是椭圆的兴趣，然后教师在黑板取两个定点，由学生动手操作，用一段细绳画出椭圆，给学生直观感知，再由学生讨论能够画出椭圆满足的几何条件，得出椭圆的定义，再由椭圆的定义演绎推导出椭圆的标准方程.高职学生的数学基础参差不齐，运用这种方法进行教学，抽象性较强，运算较繁琐，其结果往往是教师吃力，学生觉得枯燥难学，提不起学习兴趣甚至产生厌学的情绪.

学生在学习椭圆之前已经学习了圆的定义、圆的方程，了解了解析几何基本思想，知道一些用坐标法研究几何的方法；学生对椭圆也有直观感性认识，会把“扁的圆”叫做椭圆.本文作者在教学过程中，采用新的思路，设计了简便易行的“从圆转化到椭圆”的实验，引导学生通过实验、类比、猜想等方法进行探索式学习，类比学生熟悉的圆的方程，提出椭圆方程的猜想，并对猜想的正确性进行验证.通过这样的教学设计，取得了一定的教学成效.下面就椭圆的标准方程的教学设计展开介绍和讨论.

二、教学设计和过程

1.以生活为背景，通过实验探究概念

通过学生的观察和动手探究，可以对数学概念形成直观感受，有利于概念的獲取.下面是这个实验的课堂教学实录：

请每两位学生准备一个圆柱体的透明杯子（或瓶子），倒入半杯水，将杯子平放在课桌上，然后从杯子的正上方观察水面的形状.

师：请同学们观察一下，现在的水面是什么形状？

学生异口同声地回答：是一个圆.

师：让杯子向右（或向左）倾斜一个较小的角度，再看看水面是什么形状？

大部分学生：是一个椭圆.

师：把倾斜的角度加大一点，看看水面的形状发生了怎样的变化？

生：水面还是一个椭圆，不过椭圆变得更扁了.

师：思考一下，随着倾斜角度的加大，椭圆的形状在左右方向上会发生怎样的变化？前后方向呢？

生：倾斜角度越大，椭圆在左右方向上就越长，而在前后方向上不变（图1）.

通过上述实验，学生直观地认识到，圆沿着一条直径拉长可以得到椭圆，这样得到的椭圆使我们看到了椭圆与圆的关系，可以引导学生在圆的知识的基础上探索椭圆的知识.

此时再讲述课本上椭圆的定义，学生比较容易接受.

2.类比圆的方程，猜想椭圆方程

圆的方程是学生已经熟悉的知识.我们可以将椭圆与圆进行类比，根据圆的方程，猜想椭圆的方程.

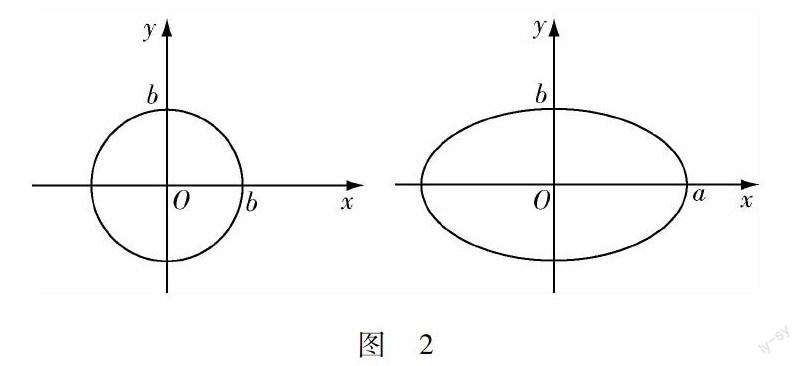
师：圆心在原点，半径为b2的圆的标准方程为x2+y2=b2，方程两边同除以b2得到什么？

生：圆的标准方程变形为x2[]b2+y2[]b2=1.

师：把这个圆横向拉长，使其在x轴上的半径增大为a，在y轴上的半径不变，仍为b，这就得到一个椭圆（图2）.类比圆的标准方程，猜想这个椭圆的标准方程是什么？

生：x2[]a2+y2[]b2=1.

到此为止，学生通过自己动手实验，认识了从圆到椭圆的转化，并且利用圆的标准方程进行类比，提出了椭圆标准方程的猜想，激发了学生的学习兴趣.

提出猜想是整个教学过程中重要的一步，但教学不能仅仅停留在这一猜想上.为了培养学生思维的严谨性，需要对上述猜想的正确性进行验证.

3.根据椭圆的定义，验证椭圆方程的猜想

由椭圆的定义可以验证上述猜想的正确性，即推导出椭圆的标准方程.

验证过程如下：

如图3建立坐标系，焦点分别为F1（-c，0）和F2（c，0），设M（x，y）为椭圆上任一点，则|MF1|+|MF2|=2a，代入坐标，得（x+c）2+y2+（x-c）2+y2=2a，化简，得（a2-c2）x2+a2y2=a2（a2-c2）.注意到a>c，记b2=a2-c2（b>0），可得x2[]a2+y2[]b2=1.这就验证了上述猜想的正确性.

由于高职学生经过了实验、类比和猜想等思维过程，特别是有了猜想作为基础，对于猜想的验证就会感到顺理成章，进而体会数学的理性与严谨，激发学生对数学知识的热爱.

进一步引导学生反过来将椭圆的标准方程与圆的标准方程进行比较，学生会发现圆可以看成是椭圆的极端情况.

通过从圆到椭圆的转化，使学生利用新旧知识的联系认识了椭圆及其标准方程，培养了学生观察问题、分析问题和解决问题的能力，达到了高职数学课堂上的素质教育目标，培养了学生的数学素养.

三、反 思

高职数学课堂教学必须打破封闭、固定的落后程式，教师要给学生充分探索空间，不要把学生的思考限制在教师预设的范围内，在教学中采用以旧引新、新旧对比的方法，引导学生在旧知识的基础上探索新知识，可以使学生感觉新知识的出现水到渠成，而过去熟知的旧知识又得到巩固与深化，使学生把握新旧知识之间的联系，从而得到系统化的知识.在椭圆的标准方程的教学设计中，还要充分了解学生的基础和知识面，往往学生的难点不一定出现在本节所要理解的内容上，如推导椭圆的标准方程时，方程的化简，在该环节上还要尽量推导细致一点才得以完成.

【参考文献】

[1]张奠宙，宋乃庆.数学教育概论[M].北京：高等教育出版社.2005.7.

[2]李振雷.椭圆定义教学实践与思考[J].数学通报2011（10）.