基于SWCC试验数据的坝体非饱和非稳态渗流与稳定性研究*

陈佳林　金　锋　陈　曦　王英男②　王育恒　任　俊

基于SWCC试验数据的坝体非饱和非稳态渗流与稳定性研究*

陈佳林①金锋①陈曦①王英男①②王育恒①任俊①

( ①北京交通大学土木建筑工程学院北京100044)

( ②中国土木工程集团有限公司北京100038)

摘要饱和-非饱和状态是土存在于自然界的真实状态，描述和解释这种状态的非饱和土力学理论在土石坝渗流、污染物传输、冻土渗流相变、边坡和路基稳定性分析等领域有着广泛的应用。非饱和土的土水特征曲线(SWCC)是非饱和土力学研究的基本内容之一，对非饱和土体渗流和稳定性分析至关重要。采用Python语言开发了非饱和渗流与稳定性分析软件包USSA和非饱和土土水特征曲线试验数据处理和模型拟合界面。对非饱和土的土水特征曲线数据进行处理，以模型拟合参数作为基本输入进行非饱和渗流场的模拟，再到非饱和土的稳定性分析，详细呈现了非饱和土渗流与稳定性分析及软件开发的全过程。基于SWCC模型的拟合参数对坝体渗流稳定性进行了分析，分析结果表明水位变化过程中坝体两侧斜坡具有明显不同的稳定性演化规律。当采用有限元强度折减法进行非饱和土斜坡稳定性分析时，最终安全系数为所有边坡安全系数演化曲线的最低包络线。

关键词非饱和土渗流和稳定性分析土水特征曲线(SWCC)Python脚本语言有限元强度折减法

陈曦(1977-)，男，博士，教授，博士生导师，主要从事计算岩土力学、特殊岩土力学、岩土工程风险方面的教学和科研.Email:xichen.geo@gmail.com

0引言

从土力学建立以来，饱和土力学一直主导着土力学的工程应用。其主要原因可以归结为以下两方面：(1)从强度角度来讲，非饱和土的强度理论通常考虑基质吸力的影响，而饱和土力学强度理论不包括基质吸力的强度贡献。因此，饱和土力学强度理论通常可以导致更加保守(或安全)的工程设计； (2)非饱和土力学理论涉及更加复杂的土-水-气相互作用，其作用机理还需要深入探究，很多理论还有待完善(Shengetal.，2013)。尽管如此，由于非饱和状态具有普遍意义，是土的真实存在状态，采用非饱和土力学理论和方法进行岩土工程问题研究的意义不仅在于获得更加精确物理描述，还在于获得针对岩土体渗流、变形和破坏机理的更加理性的解释。因此，出于实际需要，土力学研究正在从饱和土力学进入到非饱和土力学。

土水特征曲线是非饱和土力学研究区别于饱和土力学研究的主要特征之一。对于非饱和土的土水特征曲线模型，目前主要有Brooks-Corey模型、vanGenuchten模型和Fredlund-Xing模型，Luetal.(2004)的专著对上面3种模型进行了详细的介绍，并对它们的适用性进行了阐述。毛尚之(2002)对某膨胀土的土水特征曲线进行了测定，并对渗析技术和轴平移技术的结果进行了对比，初步分析了应力及吸力历史等因素对土水特征曲线的影响。卢应发等(2008)建立了一种SWCC曲线方程，并以实验获得了该方程的各项参数，试验结果表明SWCC曲线受到物质成分、塑性指数、孔隙结构、应力状态等多种因素影响，并建立了SWCC曲线与非饱和渗流曲线的相互关系。谭晓慧等(2013)认为在对SWCC曲线进行拟合时，试验数据点需要具有较大的吸力范围，才能很好地给出整条曲线的形状，否则会造成多解问题。试验点不必过于密集，但需要具有整条曲线的代表性。刘艳等(2008)研究了砂土SWCC在干湿往复条件下形成的干燥曲线与浸湿曲线滞回圈和相应的滞回行为，提出了基于热力学理论的具有一般性和普遍适用性的土水特征曲线滞后模型。通过数值模拟与实验结果的对比，验证了所提出模型的有效性。

通过非饱和土SWCC曲线可以建立基质吸力与土体体积含水率或含水量的关系，通过基质吸力和非饱和土有效应力原理可以建立非饱和土的强度理论，根据非饱和土的强度可以分析和研究饱和-非饱和土体的稳定性。目前大部分非饱和土稳定性研究都遵从以上步骤(Ngetal.， 2000; 黄润秋等， 2002；Griffithsetal.， 2005)，例如，于玉贞等(2008)和林鸿州等(2009)基于所获得的非饱和渗流场定义了非饱和土的抗剪强度，采用有限元强度折减法对坡体的稳定性进行了分析。上述分析方法的主要差别在于所采用的渗流场模型(包括SWCC模型和渗透性模型)不同或是边坡稳定性分析方法不同。例如，张磊等(2014)对于土水特征曲线方程采用了vanGenuchten方程，非饱和渗透系数模型采用的是Gardner模型，并考虑了渗流潜蚀对孔压分布和边坡稳定性的影响； 边坡稳定性分析方法则可采用极限平衡法、极限分析法、重力加载法和强度折减法等。例如，Slope/W就采用SWCC试验数据输入和极限平衡法进行降雨入渗分析。因此土水特征曲线的拟合影响了非饱和土渗流场的质量，进而又影响了非饱和土边坡的稳定性分析。各种因素可能导致SWCC的不确定性，Phoonetal.(2010)对SWCC曲线的不确定性进行了研究，建议采用对数正态随机向量来构建SWCC曲线拟合参数的概率模型。可见，SWCC曲线的不确定性会导致渗流场和边坡稳定性分析的不确定，是未来非饱和土坡稳定性分析可能面临的课题。此外，SWCC应依赖于当前孔隙比，因此随着孔隙比变化的SWCC会形成一空间曲面。

尽管SWCC曲线与孔隙比有关，本文基于时间相关的渗流-变形不完全耦合分析方法(陈曦等， 2011)，在不考虑孔隙比的情况下，从非饱和土SWCC曲线试验数据采集，到数据处理和模型参数拟合，再到非饱和土体稳定性分析，详细呈现了非饱和土渗流与稳定性分析及软件开发的全过程。通过所开发的软件对水位变化过程中均质坝体和心墙坝体渗流场和稳定性进行了分析。

1非饱和土土水特征曲线试验、模型与数据拟合

1.1非饱和土土水特征曲线试验

测定非饱和土含水量与吸力之间的关系(即土水特征曲线)可采用多种方法，李志清等(2007)介绍了6种常用方法，并评述了这些方法的优缺点。图1 所示为VJTech公司的非饱和土固结仪，该固结仪采用轴平移技术进行土水特征曲线的测量。轴平移技术是测量土体基质吸力us(即us=ua-uw)的主要方法之一，其原理是通过逐渐提升孔隙气压力ua，而用饱和高进气值材料将孔隙水压力uw维持在某个参考值，实现对基质吸力进行直接控制，并可避免对于孔隙气压力为零，基质吸力超过101kPa时陶土板中水的汽化现象。

图1　VJ Tech非饱和土固结仪的整体布置Fig. 1　VJ Tech Ltd unsaturated triaxial testing system

试验采用VJTech公司所生产的仪器，采集的数据类型为第i级基质吸力us条件下，土样排水量Vw与时间t的关系为：

(1)

当前基质吸力条件下，试验稳定后的累计排水量Vw， i+1与试验开始时刻的累计排水量Vw， i的差值为us基质吸力条件下土样的排水量ΔVw，根据试验初始时的含水量w0与土样体积V即可计算出us基质吸力条件下土样的体积含水率w：

(2)

本次试验所施加的基质吸力等级依次为1kPa， 3kPa， 5kPa， 10kPa， 20kPa， 50kPa， 150kPa， 250kPa，所用陶土板的进气值为5bar(1bar=100kPa)， 24h内的排水量不超过0.1cm3时认为达到吸力平衡。图2 所示为各级吸力下砂土的累计排水量随时间的变化曲线。对于砂土，在初始较小的基质吸力(如1kPa)作用下，就会产生较大的排水量，而此时的水流驱动力较小，因此排水时间比较长(约17d)； 之后各级吸力下的排水量明显减少，达到吸力平衡的时间也较短(约3～5d)。

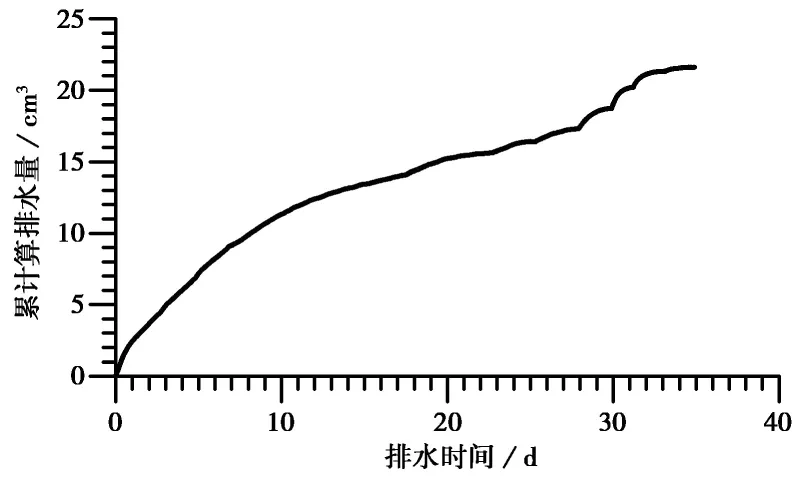
图2　典型砂土累计排水量随时间的变化关系Fig. 2　Accumulated quantity of water outflow varying with time for typical sand

1.2常用的土水特征曲线模型

常用的土水特征曲线模型有Brooks-Corey(1964)模型，vanGenuchten(1980)模型和Fredlund-Xing(1994)模型。这些模型中部分参数(如饱和含水量θs和残余含水量θr等)具有实际物理意义，也有部分参数没有物理意义。下面仅详细给出vanGenuchten模型的具体表达式。

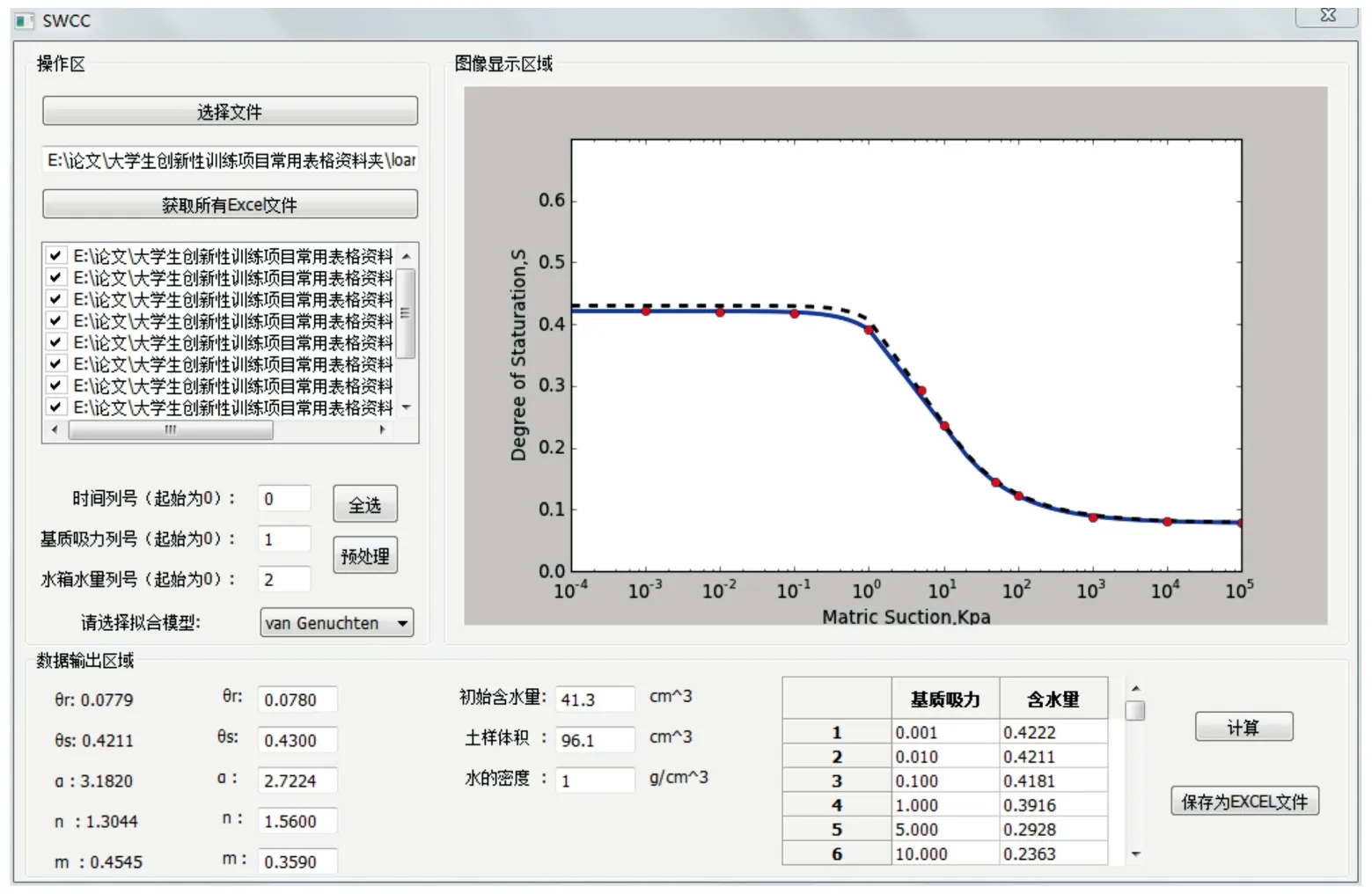
图3　SWCC试验数据拟合结果Fig. 3　Fitting results of the SWCC experiment

vanGenuchten于1980年提出了一个土水特征曲线的模型(简称VG模型)。相比BC模型，VG模型具有连续平滑曲线，在进气压力值和趋近残余含水量状态时具有较好的平滑过渡，因此得到了广泛的应用。VG模型表达式如下：

(3)

或表示为标准化的体积含水量Θ

(4)

式中，av、nv和mv为经验系数，mv通常简化为mv=1-1/nv。VG模型是上述3参数的模型，对于同一干密度条件下的土，θs和θr可由土的基本物理力学试验直接测出，当没有θs和θr的实测数据时，可将该模型按5参数模型进行拟合。

1.3土水特征曲线数据拟合与界面开发

进行土水特征曲线试验时可得到一系列的Excel数据文件，每个Excel文件对应某一级基质吸力作用下的排水过程，或者说每个Excel文件表示土水特征曲线上的一个数据点(us，θ)。点击“选择文件夹”选择存储SWCC数据文件的文件夹； 接下来点击“获取所有Excel文件”将该文件夹中的Excel文件导入到列表窗口，并勾选列表窗口的Excel数据文件，每个Excel文件对应土水特征曲线上的一个数据点。同时需要填写本试验的初始水的体积和试样体积。对数据点整理和认定后生成一个新的Excel文件，对应着不同基质吸力条件下的排水量，组合成一个新的数据表即可进行拟合。图3 展示了SWCC可视化界面，具体分为操作区、图像显示区域和数据输出区域。可视化系统所采用的拟合方法为非线性最小二乘法，图像显示区域给出了根据试验数据拟合的SWCC曲线，同时将拟合的模型参数传递给数值模拟界面。

2非饱和渗流的有限元求解与非饱和土稳定性分析

采用Richards方程进行非饱和土渗流模拟已经得到了广泛的认可。Richards方程有3种基本格式，即压力水头格式(h-form)、混合格式(mixedform)和体积含水量格式(θ-form)。其中压力水头格式在实际工程中的应用更为广泛。

非饱和渗流的水力传导系数可采用Mualem式(1976)，即：

(5)

式中： 饱和水力传导系数ks为常数；kr(Θ)为相对渗透张量， 为有效饱和度Θ的函数； 而非饱和渗流的水力传导系数则随体积含水量的减小而迅速衰减。

压力水头格式(h-form)的Richards方程如下：

(6)

式中，(x，t)∈Ω×(0，T]，s为源汇项；η为比存储量(即土水特征曲线的导数)。

(7)

式中： γw为水的单位重度； mw为土水特征曲线的斜率。空间离散和时间差分后可得h-form的Richards有限元方程的修正Picard迭代公式：

(8)

式中，

(9)

其中，下标n表示时间步指标； m表示修正Picard的迭代步指标； M，C分别为质量矩阵和水力传导特征矩阵。

非饱和土坡稳定性分析方法主要分为3大类，即时间无关的定性分析方法，时间相关的渗流与变形不完全耦合分析方法和时间相关的渗流与变形完全耦合分析方法。尽管完全耦合分析方法已经成为发展趋势，从发展成熟程度和计算效率角度考虑，时间相关的渗流与变形不完全耦合分析方法仍为当前的主流分析方法，其基本思路是先进行非饱和渗流分析，基于某一时刻的瞬态渗流场，再采用极限平衡法或强度折减有限元法进行饱和-非饱和土坡的稳定性分析。

非饱和土边坡稳定性评价需要采用非饱和土抗剪强度理论。缪林昌等(1999)曾对非饱和土的抗剪强度进行了研究，提出了基于试验数据拟合的双曲模型。而常用的非饱和土的抗剪强度理论仍以Bishop和Blight强度理论以及Fedlund强度理论为主。根据非饱和土的有效应力原理：

(10)

式中：χ为与饱和度(Sr)相关的参数。则Bishop和Blight强度理论可表示为：

(11)

Fredlund强度理论则表示为：

(12)

式中，c′， φ′分别为土的有效黏聚力和有效内摩擦角; φb是一个描述基质吸力对剪切强度贡献的角度，可见，Fredlund强度理论区别对待了φb对基质吸力影响，而目前各种非饱和土强度理论的主要差别在于χ和tanφb的选取的不同。为了计算方便，非饱和土的抗剪强度也常记为：

(13)

式中，“假黏聚力”c″由c′和基质吸力影响(即ustanφb)两部分组成。式(13)中，根据Shengetal.(2011)，tanφb具有不同的定义，例如:

(14)

式中，当参数κ取为1.0，Fredlund-Fredlund公式退化为Fredlund-Oberg公式。应用强度折减法时，需要进行如下折减：

(15)

式中，SRF为强度折减因子。需要强调的是，当在c″考虑基质吸力的影响时，由于积分点上的基质吸力不同，c″对于每个单元并不是常数，需要进行均匀化处理，取积分点的平均值作为该单元的黏聚力指标。

与传统的极限平衡法和极限分析法相比，有限元强度折减法具有一些优势，除了能够给出边坡的安全系数，还可以得到位移、应力、应变场，塑性屈服点的分布以及边坡失稳破坏的全过程。由于有限元强度折减法需要处理更多的信息，相比极限平衡法和极限分析法，自然需要更多的计算时间，因此如何提高有限元强度折减法的计算效率成为需要关注的一个问题(Chenetal.，2014)。

3非饱和土渗流与稳定性分析程序USSA的计算流程

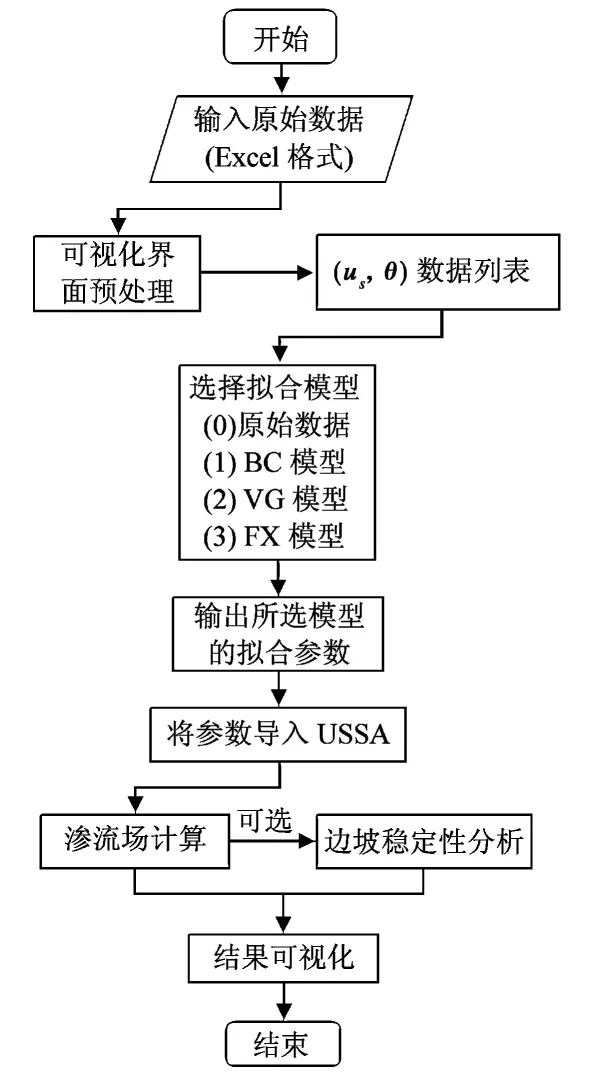
图4　USSA非饱和土渗流与稳定性分析软件包的分析流程Fig. 4　Unsaturated seepage and stability analysis flowchart for USSA software package

基于上述理论方法，开发了非饱和土渗流与稳定性分析软件包。图4 所示为非饱和土渗流与稳定性分析软件包USSA的分析和计算流程。首先给定一系列初始的Excel文件，生成绘制SWCC曲线所需要的两列数据(us，θ)，如1.3节所述。根据非饱和土的类型选择合适的SWCC模型进行试验数据拟合，或直接采用原始数据(us，θ)进行拟合或插值使用。这里默认选取Mualem公式为非饱和水力传导系数公式，当然可进一步扩展并加入其他非饱和水力传导系数公式。根据选用的SWCC模型和拟合得到的模型参数进行非饱和渗流场模拟，当需要进行土体稳定性分析时，可以在进行渗流场计算的同时，进行稳定性分析。最后可视化显示非饱和渗流场，含水量分布，位移场和塑性点分布等。USSA软件的用户界面和SWCC界面都采用Python语言开发，计算程序则采用FORTRAN语言开发。目前，Python作为一种开源的脚本编程语言，已经得到了广泛的应用。

4数值应用

4.1均质土坝算例

图5为均质土坝，即坝身土体和坝基土体土性参数相同。土体有效弹性参数取E′=10MPa，ν′=0.3； 摩尔-库仑有效塑性参数取为c′=10kPa，φ′=20°(此处采用相关塑性流法则)； 自然和饱和重度分别为17kN·m-3和20kN·m-3，ks均为1e-6m·s-1； 非饱和渗流土水特征曲线采用VG模型，模型参数θs，θr，av(1·kPa-1)和nv(mv=1-1/nv)分别为0.367， 0.187， 1.0和1.53。土坝左右边坡坡度分别为1︰1.8和1︰1.4， 土坝左侧初始水位为0m，右侧初始水位为7.05m。在此初始条件下达稳态渗流，相应的阴影图(图6)。右侧水位从初始水位以1m·d-1的速度下降，最后水位为0m。

图5　土坝有限元网格划分与几何尺寸Fig. 5　Finite element mesh and geometry of soil dam

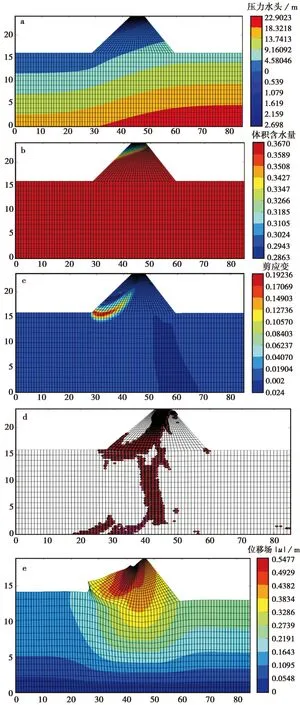
图6　初始高水位时的阴影图Fig. 6　At the initial water level， contour plotting for(a) Pressure head; (b) Volumetric water content; (c) Shear strain; (d) Plastic zone; (e) Displacement modulus |u|a.压力水头； b.体积含水量； c.剪应变； d.塑性区； e.位移场|u|

从图6a、图6b可知，自由液面以下土体处于饱和状态，自由液面以上坝体的体积含水量随着高程增加而逐渐减小。在初始水位和渗流条件下，土坝左侧坡体的安全系数最小，为FOS=1.528，失稳时的剪应变、塑性点分布和位移场|u|分别如图6c、图6d和图6e所示。

图7　最低水位时的阴影图Fig. 7　At the final water level， contour plotting for(a) Pressure head; (b) Volumetric water content; (c) Shear strain; (d) Plastic zone; (e) Displacement modulus |u|a.压力水头； b.体积含水量； c.剪应变； d.塑性区； e.位移场|u|

图7所示为右侧水位下降为0m时的阴影图。从图7a、7b可见，尽管土坝左右两侧水位都为0m，由于时间效应和土体的持水特性，坝体中部自由液面的高度要大于两侧的高度。此外，最危险的滑坡从左侧转移到右侧，如图7c、7d和7e所示，此时坡体安全系数为FOS=1.398。图8 完整地呈现了水位下降过程中，土坝坡体安全系数的变化过程，即安全系数先稳定增加，达到某一值(FOS=1.567)之后开始迅速减小，也正是从这一点开始，最危险的滑坡从左侧转移到右侧。因此，可以推断，当水位从初始高度开始下降时，左右侧坡体中的自由液面开始下降，坡体中非饱和土体比例都在增加，而自由液面以下的饱和土体比例逐渐减小。由于饱和土体自重大、强度低，而非饱和土体自重较小，强度较高。自由液面下降导致左侧坡体安全系数逐渐增大，而对于右侧坡体则相对复杂，这是由于水位下降过程中，右侧水体对坡面的正压力也在下降，不利于坡体的安全。在水位较高时，右侧水体对坡面的正压力较大，导致右侧坡体的安全系数大于左侧坡体的安全系数，但随着水位的下降，右侧坡体的安全系数迅速减小，并在水位下降超过4m时，开始小于左侧坡体的安全系数。因此，图8 所示的安全系数变化曲线可以看成是左侧坡体和右侧坡体安全系数的交叉组合变化曲线中安全系数最小的部分。为了获得左右边坡完整的安全系数变化曲线，可采用极限平衡法进行求解。如何采用有限元强度折减法获得左右边坡完整的安全系数变化曲线而不产生明显的结果偏差还有待研究。

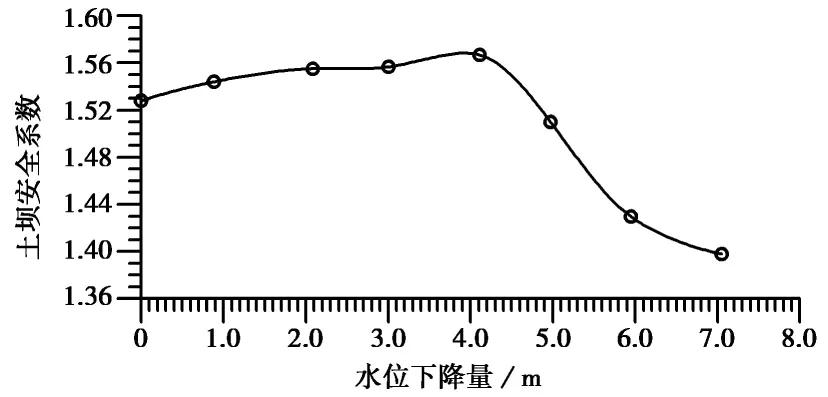
图8　水位降低过程中均质土坝安全系数的变化曲线Fig. 8　Variation curve of safety factor(FOS)with the fall of water level for homogeneous dam

4.2非均质土坝算例

对于非均质土坝，仍采用上述图5 所示的均质土坝的有限元网格划分，但坝体和坝基则分别采用非饱和土数据库UNSODA中编号为1183的黏土和编号为3091的砂质壤土(Nemesetal.，1999)。采用图3 所示的SWCC数据处理和模型拟合界面分别对这两种非饱和土的试验数据进行VG模型拟合，得到的水力参数如表1所示，拟合曲线如图9 所示。坝体坝基弹性参数均为E′=10MPa，ν′=0.3； 采用摩尔-库仑强度模型，坝体参数为c′=30kPa，φ′=25°，坝基为c′=20kPa，φ′=35°； 坝体坝基自然和饱和重度分别为17kN·m-3和20kN·m-3。

表1　非均质土坝水力参数

图9　基于VG模型拟合的SWCC参数Fig.9　Fitted parameters of SWCC based on VG modela. 编号为1183的粘土; b. 编号为3091的砂质壤土

非均质土坝左右侧初始水位与上述均质土坝相同，但右侧水位从初始水位以0.01m·d-1的速度下降，最后水位为0m。图10 所示为水位下降过程中，土坝坡体安全系数的演化过程。与均质土坝中安全系数的变化相似，当水位下降4m左右时，潜在破坏坡体从左侧转移到右侧。不过由于坝体和坝基的强度较高，坡体的安全系数也在较大值附近波动。

图10　水位降低过程中非均质土坝安全系数的变化曲线Fig. 10　Variation curve of safety factor(FOS)with the fall of water level for heterogeneous dam

5结语

非饱和状态是土的真实存在状态。非饱和土体渗流和稳定性分析是非饱和土力学研究的重要内容。本文从非饱和土SWCC曲线试验开始，到SWCC模型参数拟合，再到渗流和稳定性分析，详细呈现了整个分析过程，开发了SWCC数据处理和模型拟合界面以及渗流稳定性分析程序。通过数值算例，得到了一些结论：

(1)由于饱和土和非饱和土具有不同的抗剪强度和容重，非饱和渗流场的模拟精度对坝体稳定性分析具有显著的影响。抗剪强度的评价也是基于不同应力点的“假黏聚力”的定义，根据不同的原理定义的“假黏聚力”不同，因此也会对坝体稳定性的分析结果产生影响。

(2)水位下降过程中，坝体渗流场发生相应的变化，两侧坝体斜坡的稳定性具有明显不同的演化规律。一般来说，坝体下游斜坡的稳定性影响因素单一，主要随着上游水位降低非饱和区逐渐增加，导致下游斜坡稳定性逐渐增加； 而上游斜坡稳定性由增加的非饱和区和撤离的水压共同支配。当采用有限元强度折减法进行非饱和土斜坡稳定性分析时，安全系数为所有边坡安全系数演化曲线的最低包络线。

参考文献

ChenX，LiuCJ. 2011.Stageddevelopmentoffiniteelementmethodsforstabilityofunsaturatedsoilslopes[J].ChineseJournalofGeotechnicalEngineering， 33(S1)： 380～384．

ChenX，WuYK，YuYZ，etal. 2014.Atwo-gridsearchschemeforlarge-scale3-Dfiniteelementanalysesofslopestability[J].ComputersandGeotechnics，62： 203～215．

GriffithsDV，LuN. 2005.Unsaturatedslopestabilityanalysiswithsteadyinfiltrationorevaporationusingelasto-plasticfiniteelements[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics，29(3)： 249～267．

HuangRQ，QiGQ. 2002.Theeffectofunsaturatedsoilsuctiononslopestability[J].JournalofEngineeringGeology，10(4)： 343～348．

LiZQ，LiT，HuRL，etal. 2007.MethodsfortestingandpredictingofSWCCinunsaturatedsoilmechanics[J].JournalofEngineeringGeology，15(5)： 700～707．

LinHZ，YuYZ，LiGX，etal. 2009.Onapplicationofsoil-watercharacteristiccurvestolandslideforecast[J].ChineseJournalofRockMechanicsandEngineering， 28(12)： 2569～2576．

LiuY，ZhaoCG. 2008.Hysteresismodelforsoil-watercharacteristiccurves[J].ChineseJournalofGeotechnicalEngineering，30(3)： 399～405．

LuN，LikosWJ. 2004.Unsaturatedsoilmechanics[M].Wiley．

LuYF，ChenGF，LuoXQ，etal. 2008.Studyofsoil-watercharacteristicalcurveanditsinfluentialfactors[J].RockandSoilMechanics， 29(9)： 2481～2486．

MaoSZ. 2002.Astudyonsoil-watercharacteristiccurveofunsaturatedsoil[J].JournalofEngineeringGeology，10(2)： 129～133．

MiaoLC，YinZZ. 1999.Shearstrengthofunsaturatedsoils[J].RockandSoilMechanics，20(3)： 1～6．

NemesA，SchaapMG，LeijFJ. 1999.TheUNSODAunsaturatedsoilhydraulicdatabase(Version2.0)[R].USSalinityLaboratory，Riverside，CA．

NgCWW，PangYW. 2000.Influenceofstressstateonsoil-watercharacteristicsandslopestability[J].JournalofGeotechnicalandGeoenvironmentalEngineering，126(2)： 157～166．

PhoonKK，SantosoA，QuekST. 2010.Probabilisticanalysisofsoil-watercharacteristiccurves[J].JournalofGeotechnicalandGeoenvironmentalEngineering，136(3)： 445～455．

ShengDC，ZhouAN，FredlundDG. 2011.Shearstrengthcriteriaforunsaturatedsoils[J].GeotechnicalandGeologicalEngineering，29(2)： 145～159．

ShengDC，ZhangS，YuZW. 2013.Unansweredquestionsinunsaturatedsoilmechanics[J].ScienceChinaTechnologicalSciences，56(5)： 1257～1272．

TanXH，YuW，ShenMF，etal. 2013.Experimentalstudyandcurvefittingofsoil-watercharacteristiccurve[J].RockandSoilMechanics， 34(S2)： 51～56．

YuYZ，LinHC，LiRJ，etal. 2008.Stabilityanalysisofunsaturatedsoilslopeundertransientseepageflowstate[J].RockandSoilMechanics，29(11)： 2892～2898．

ZhangL，ZhangLL，ChengY，etal. 2014.Slopestabilityunderrainfallinfiltrationconsideringinternalerosion[J].ChineseJournalofGeotechnicalEngineering，36(9)： 1680～1687．

陈曦，刘春杰. 2011. 逐步完善的非饱和土边坡稳定性有限元分析方法[J]. 岩土工程学报， 33(S1)： 380～384．

黄润秋，戚国庆. 2002. 非饱和渗流基质吸力对边坡稳定性的影响[J]. 工程地质学报，10(4)： 343～348．

李志清，李涛，胡瑞林，等. 2007. 非饱和土土水特征曲线(SWCC)测试与预测[J]. 工程地质学报，15(5)： 700～707．

林鸿州，于玉贞，李广信，等. 2009. 土水特征曲线在滑坡预测中的应用性探讨[J]. 岩石力学与工程学报， 28(12)： 2569～2576．

刘艳，赵成刚. 2008. 土水特征曲线滞后模型的研究[J]. 岩土工程学报，30(3)： 399～405．

卢应发，陈高峰，罗先启，等. 2008. 土-水特征曲线及其相关性研究[J]. 岩土力学， 29(9)： 2481～2486．

毛尚之. 2002. 非饱和膨胀土的土-水特征曲线研究[J]. 工程地质学报，10(2)： 129～133．

缪林昌，殷宗泽. 1999. 非饱和土的剪切强度[J]. 岩土力学，20(3)： 1～6．

谭晓慧，余伟，沈梦芬，等. 2013. 土-水特征曲线的试验研究及曲线拟合[J]. 岩土力学， 34(S2)： 51～56．

于玉贞，林鸿州，李荣建，等. 2008. 非稳定渗流条件下非饱和土边坡稳定分析[J]. 岩土力学，29(11)： 2892～2898．

张磊，张璐璐，程演，等. 2014. 考虑潜蚀影响的降雨入渗边坡稳定性分析[J]. 岩土工程学报，36(9)： 1680～1687．

UNSATURATEDTRANSIENTFLOWINDAMANDITSSTABILITYANALYSISUSINGSWCCEXPERIMENTALDATA

CHEN Jialin①JIN Feng①CHEN Xi①WANG Yingnan①②WANG Yuheng①REN Jun①

(①SchoolofCivilEngineering，BeijingJiaotongUniversity，Beijing100044)

(②ChinaCivilEngineeringConstructionCorporation，Beijing100038)

AbstractSaturated-unsaturated state is a natural state of soils. Hence, unsaturated soil mechanics has wide applications in seepage analysis of earth and rockfill dam, contaminant transport, seepage and phase transform of frozen soil, and stability analysis of slope and embankment. As a fundamental relationship, the soil-water characteristic curve(SWCC)plays an essential role in the research of unsaturated soil mechanics. Python language is employed to develop the unsaturated seepage and stability analysis(USSA)software as well as the graphic user interface(GUI)for data processing and data fitting of SWCC curve. Based on a practical slope example, the whole analyzing process is described in details. It is from the data processing and data fitting of SWCC curve to unsaturated seepage analysis and stability analysis. The stability of dam under unsaturated seepage is conducted using the fitted parameters of SWCC model. The numerical results show that the stability evolutions of two dam slopes are quite different under the changing process of water level. When applying the shear strength reduction finite element method to the slope stability of unsaturated soil, the final FOS appears to be the lowest envelope of those FOS curves of all slopes．

Key wordsUnsaturated soil， Seepage and stability analysis， Soil-water characteristic curve(SWCC)， Python script language， Shear strength reduction finite element method

DOI:10.13544/j.cnki.jeg.2016.02.012

* 收稿日期：2015-02-04; 收到修改稿日期： 2015-04-04.

基金项目：国家自然科学基金项目(51379103)， 国家“973”项目课题(2012CB026104)， 教育部博士点新教师基金(20110009120020)资助.

第一作者简介：陈佳林(1994-)，男，学士，主要从事岩土工程及结构工程方面的科研和软件开发工作. Email：12231037@bjtu.edu.cn

中图分类号：TV139.14

文献标识码：A