基于FLO-2D数值模拟的泥石流流动与堆积影响因素研究*

梁鸿熙　尚　敏　徐　鑫

(三峡大学土木与建筑学院宜昌443002)

基于FLO-2D数值模拟的泥石流流动与堆积影响因素研究*

梁鸿熙尚敏徐鑫

(三峡大学土木与建筑学院宜昌443002)

摘要泥石流和普通的山体滑坡不同，它是发生在山区的一种含有砂土和石块的暂时性水流，具有宾汉体的性质和运动阻塞双重特性，国内外众多学者在流动学实验及流动学模型的基础上，对数值模拟方法进行了大量研究，通过泥石流的灾害范围、运动速度、运动时间与实际情况进行对比，开发出适用于泥石流预报的数值模拟程序，FLO-2D就是其中之一。工程实践证明，在对泥石流组成物质的流动特性研究基础上，对泥石流移动及沉积特性进一步研究是非常重要的。本文运用FLO-2D流动模型数值模拟方法对泥石流的移动特性进行模拟，以此分析泥石流流动及堆积特性与黏性系数和屈服应力的关系。通过分析得到：随着黏性系数的增大，泥石流流速呈非线性减少； 屈服应力作为影响泥石流发生及停止的因素，随着屈服应力的增大，流深也随着增大，但在泥石流移动特性中，屈服应力对泥石流流速的影响并不明显； 随着黏性系数的增加，泥石流冲击力减小，而随着屈服应力的增加，泥石流的冲击力则增大。

关键词数值模拟FLO-2D黏性系数屈服应力

0引言

泥石流和普通的山体滑坡不同，它是发生在山区的一种包含泥砂、块石的固液两相流体，其介于块体重力运动和水流等液体水力运动之间，呈黏性层流或稀性紊流状态。据有关学者的大量研究表明，泥石流具有宾汉体的性质和运动阻塞双重特性。O’Brienetal.(1985)、Iversonetal.(1997)、Imranetal.(2001)在对泥石流进行分析时，根据泥石流所具有的移动特性，把它作为一种流体来进行分析研究。由于工程地质、气象等要素的综合作用影响，使得泥石流运动模型的研究变得困难。同时，由于泥石流运动速度快和移动距离长及受灾范围广，使得泥石流的预报工作难度也非常大。但是，泥石流往往突然爆发，来势凶猛，而且其能量巨大，破坏性强，还具有运动过程的直进性、阵流性、非定常性、不均匀性和侵蚀性等特点。有时形成危害较大的阵流，严重威胁人民群众的生命财产安全。为了使泥石流灾害区的损失最小化，所以对灾害区进行提前灾害预报是十分必要的。由于泥石流流动与堆积特性直接决定泥石流的破坏及影响范围，也是影响预测预报的主要因素。因此，对两者的研究对泥石流的预测预报是至关重要的，有较强的实际应用价值。

近年来，泥石流危险性评价得以发展，研究成果的实践意义也得到很大提高。研究泥石流的主要方法有野外调查、数值模拟以及实验研究等多种方法。由于数值模拟方法的成本低，而且重复性强，在近年来被广泛运用。在数值模拟方面，尤其对泥石流主要致灾区——堆积区的研究较多。其中，日本学者石川芳治等(1991)通过水工模型试验用数值模拟研究了泥石流的堆积泛滥范围，罗元华(1998)考虑侵蚀因素的控制方程，进行泥石流堆积数值模拟。还有其他众多学者在流动学实验及流动学模型的基础上，张鹏等(2014)、Wuetal.(2013)、Linetal.(2005)、Bertoloetal.(2005)运用FLO-2D模型较好地模拟了小流域泥石流运动淤积过程。Johnsonetal.(1970)提出利用宾汉体黏性流解释泥石流运动过程，建立泥石流运动控制方程，计算出泥石流最大流速的分布。Marcel(2006)等采用有限差分方法对泥石流沟谷进行数值模拟确定了泥石流的危险范围，并在此基础上进行了危险性分区。唐川等(1993)、唐川(1994a，b，c)运用剖开算子有限差分法对泥石流进行计算模拟，得出泥深及流速的分布，对泥石流危险度进行评价。

在众多学者研究的基础上，本文使用FLO-2D软件加上雨量资料、数值地形资料与相关参数模拟泥石流的流动情况，以2011年湖北黄石富水河地区青石沟所发生泥石流为数值模拟原型，配合现有的地质调查资料，来模拟泥石流的黏性流动参数及屈服应力变化情况，分析泥石流的流动及沉积特性。

1研究区概况

青石沟位于阳新沿镇，属于富水河流域，流域面积5310km2，属北亚热带气候区，干流长196km，河道总落差613m。流域内5km以上支流有130条，其中一级支流30条，二级支流52条，地下水丰富，但地下水类型与分布规律呈现多样性。研究区内沟谷呈南北向展布，形态多呈“V”字形，地势北高南低，相对高差198m，为泥石流形成的典型地形。根据气象资料显示，该地区降雨量丰富，年均降雨量1389.6mm。年均降雨日147个，夏季最多， 4～7月平均降雨量739.9mm，雨量多，强度大，常造成洪涝灾害，此气象条件极有利于泥石流的形成。在2011年7月12日，当日累计降雨量超过250mm，当天傍晚6点32分左右爆发了泥石流，方量约为1.5×104m3，为小型泥石流，整个流径约为556m，但并未造成人员及财产损失。

根据现场调查，青石沟泥石流形成区内为三面环山、一面出口的圆形宽阔地段，纵长约200m，周围山坡陡峭多为30°～60°的陡坡，经测算汇水面积约10000m2。陡坡坡体岩体破碎，植被覆盖率较低； 斜坡常被冲沟切割强烈，形成较多不稳定斜坡，崩塌与滑坡时有发生。加之该地区出露的岩层主要为震旦系、奥陶系灰岩、砂岩与泥岩互层，岩层岩性较软，易受风化侵蚀，形成第四系崩坡积松散堆积物，构成了泥石流物质来源，为泥石流的爆发提供了丰富的物质基础。流通区纵长约为200m，多为狭窄而深切的峡谷或冲沟，谷壁陡峻而纵坡降大，平均坡度为25°，泥深为2～3m，由于所夹挟物质多为松散堆积物，并未对原沟谷产生较强烈的下切作用。堆积区纵长约为156m，位于青石沟的沟口处，地形较为开阔、平缓，平均坡度为10°，堆积厚度为5～8m，形成面积为2000m2的堆积区。

2FLO-2D数值模拟

2.1概要

FLO-2D是美国科罗拉多州立大学的O’Brienetal.(1993)用有限差分法来求解运动控制的程序，它可以在工程设计、洪水灾害管理、泥石流等问题上得到很好运用。为了求取流动深度及流量，我们采用的数值地形为规则网格单元，并且每个网格都给定固定单一的高程和粗糙系数，然后输入各项参数进行计算，在FLO-2D程序中，有以下几项假设及限制：

(1)差分时间间隔内为稳定流,

(2)水道断面和粗糙度是规则的,

(3)净水压力分布,

(4)每一个网格有单一的高程及N值,

(5)无法模拟水道的刷深现象,

(6)无法模拟上游崩塌可能对泥石流造成的影响,

(7)假定泥石流流通区为定沟床模式，故无法模拟沟道的侵蚀现象。

2.2建模

FLO-2D的连续方程(1)及运动方程(2)、(3)如下所示：

(1)

(2)

(3)

上式中，式(1)控制泥石流或洪水以及质量守恒，其中，t为时间；i为降雨强度；u为X方向的平均流速；v为Y方向的平均流速；h为流动深度。

式(2)与式(3)为力平衡的动量方程，动力波模式为动量方程主体，扩散波模式为省略式中最后3项，运动波模式则是省略式中的压力梯度。FLO-2D提供动力波模式及扩散波模式来模拟洪水与泥石流问题。式中，g为重力加速度；Sfx及Sfy为摩擦坡降；Sox及Soy为底床坡降。

针对泥石流的流变方程，O’Brienetal.(1985)设计了一套关于泥石流的计算方程式，如式(4),式(5)所示：

(4)

(5)

上式中，τy为屈服应力；η为黏性系数；C为惯切剪应力；K为层流阻滞系数，取值范围24～50000；ρ为泥石流密度；g为重力加速度；n为曼宁n值，参考FLO-2D手册；h为流深；V为平均流速。

又有式(6)～式(7)如下：

(6)

(7)

式中，Cv为泥石流体积浓度，其中经验系数α1、α2、β1、β2取值通过查阅相关FLO-2D手册资料确定，其取值如表2所示。

表1　不同沉积物浓度流动特性表

表2　FLO-2D 输入参数值

FLO-2D中按体积浓度和流动特性分为4个等级，分别是滑坡，泥石流，泥流，洪水(表1)。研究中，根据对现场泥石流的调查情况，取表中的0.45作为体积浓度。

2.3输入变量

本文以2011年富水河流域青石沟泥石流数据为基础，选取参数进行计算。由于泥石流发生机制的复杂性，我们选取泥石流灾害地区流域面积比较大的青石沟流域，同时对该流域的资料进行整理利用。根据实测情况，该区断面是由形成区坡度为38°、流通区坡度15°、堆积区坡度6°所构成的长556m，高198m斜面(图1)，在资料使用中，为了便于掌握泥石流堆积特性，距离为556m以后的视为平地。

图1　流域横截面简图Fig. 1　Basin cross section

流量按照实际的流域面积和降雨强度来计算，泥石流发生时当日累计雨量超过250mm，降雨强度105mm·h-1。通过计算得到，流域最大流量为1.89m3·s-1。

为了获得移动特性和堆积特性随着黏性系数和屈服应力的变化关系明显的规律，研究中各取标准黏性系数和屈服应力值的10倍、100倍的差异值来进行模拟分析。表2为本次模拟所涉及的主要参数取值，各参数的取值采取现场原位试验、室内试验与经验参数相综合的办法。并且，为了分析随着黏性系数及屈服应力的变化泥石流流动和沉积变化特点，黏性系数依次为η0、10η0、100η0，屈服应力依次为τy0、10τy0、100τy0，流入流量，体积浓度、运移时间等其他条件保持不变。

3分析结果

3.1泥石流移动及沉积特性与黏性系数的关系

从图2 中可以看出，泥石流移动速度更依赖于斜坡坡角。同时，随着黏性系数的增加，移动速度呈减小的趋势，当η0较小时，不同断面倾斜角的移动速度呈现较大的差异，而随着η0的增大，不同断面倾斜角的移动速度差异慢慢减小。

图2　泥石流流速与黏性系数关系图Fig. 2　Velocity of debris flow according to viscosity

图3为泥石流流深与黏性系数变化关系图，泥石流的流深并没有随着倾斜角度的不同而呈现较大的差异。黏性系数越大，粒子间的凝聚力增大，流速越来越小，但是流深却不断变大。

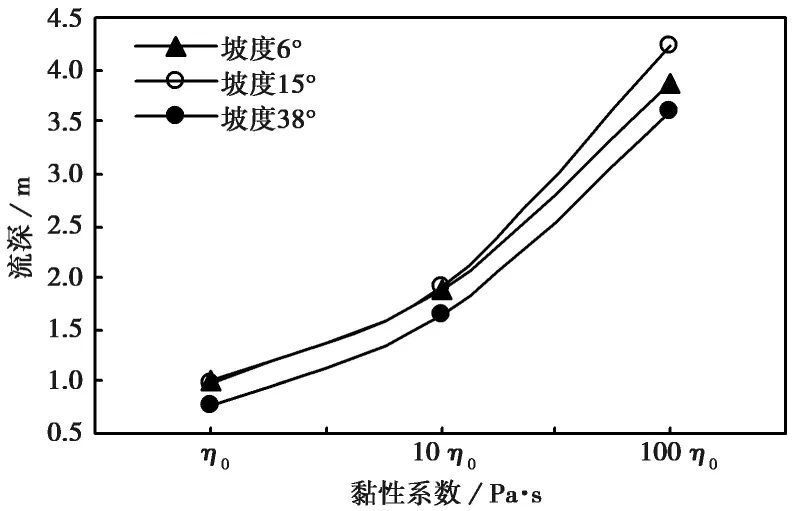
图3　泥石流流深与黏性系数关系图Fig. 3　Flow depth of debris flow according to viscosity

图4为泥石流流动范围随着黏性系数变化结果图，其流动范围结果图是根据泥石流发生当日，根据降雨情况及其他资料，通过数值分析得到的。分析表明黏性系数越大，流动距离和扩散范围则越小，当黏性系数为100η0时，在堆积区坡角为6°的坡面中，其活动范围在没有达到平地的时候已经停止，这是由于黏性增加，泥石流粒子间的凝聚力增加，泥石流的流动阻力增大。

表3为FLO-2D模拟得出的泥石流沉积距离、

平均沉积宽度、最大沉积宽度和堆积面积变化情况。随着黏性系数的变大，泥石流沉积距离、沉积宽度，沉积面积逐渐减小。随着黏性系数的增加，移动速度、移动距离、扩散范围所表现出来的反比例现象，是由于泥石流本身移动特性和沉积特性所影响的。

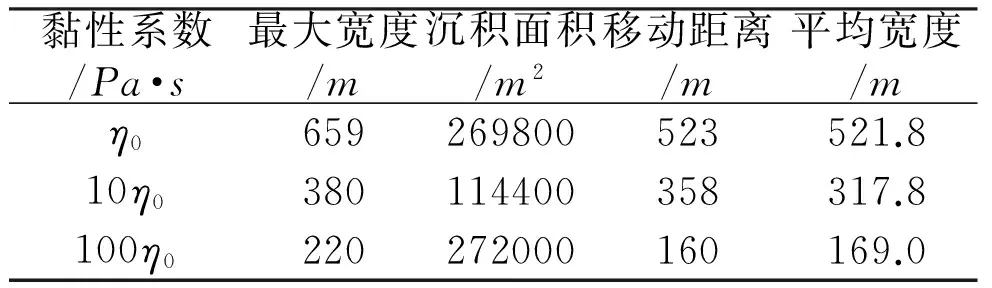
表3　泥石流运动特征与黏性系数关系表

图4　不同黏度的泥石流扩散范围Fig. 4　Spreading range of debris flow according to viscositya. η0； b. 10η0； c. 100η0

随着泥石流的流动，为了模拟分析其危险范围，需要对泥石流的冲击力进行分析。FLO-2D中所用到的泥石流冲击力计算公式如(8)～式(10)，它受到流体密度，冲击角度等多种因素的综合影响。

(8)

k=1.261eCw

(9)

F=Pih

(10)

式中，Pi为冲击压力，通过流体密度ρf、系数k、网格中最大移动速度V来计算。单位面积冲击力F为Pi所对应的网格最大流深h的乘积。即冲击力与最大移动速度的平方和流深呈正比例关系。

图5是利用不同黏性系数时堆积部的冲击力和表3数据所绘制的，结合图4 的计算结果可知，黏性系数越大，冲击力则减小，这是由于移动速度快速减小的原因所导致。

图5　冲击力、沉积区与黏性系数关系图Fig. 5　Impact force and depositional area according to viscosity

3.2泥石流移动及堆积特性与屈服应力的关系

图6为形成区、流通区和堆积区中泥石流流速随屈服应力变化关系图。尽管屈服应力越大，但是移动速度的变化量并不是很明显，而在屈服应力相同的情况下，倾角越大，其流速也越大。所以，相对于屈服应力而言，倾角对流速的变化影响更大。

图6　泥石流流速与屈服应力关系图Fig. 6　Velocity of debris flow according to yield stress

图7　泥石流流深与屈服应力关系图Fig. 7　Flow depth of debris flow according to yield stress

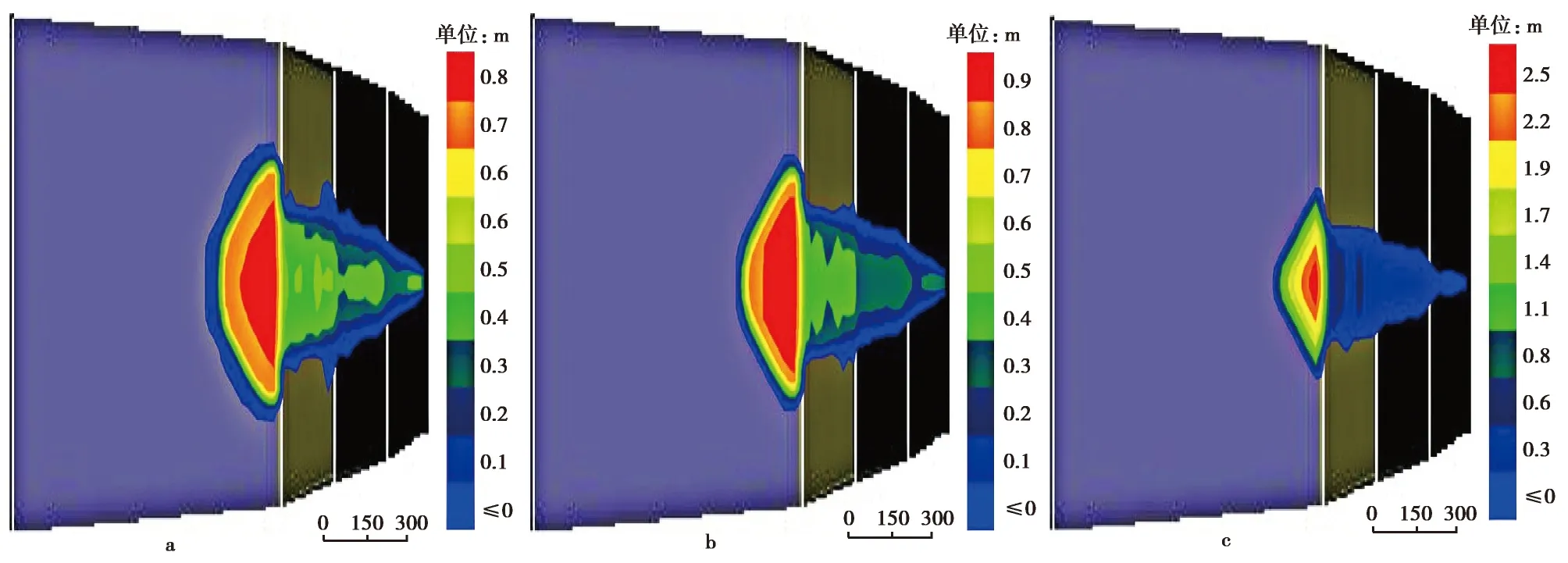
图9　不同屈服应力下泥石流的扩散范围Fig. 9　Spreading range of debris flow according to yield stressa. τy0； b. 10τy0； c. 100τy0

图7为不同屈服应力状态下，流深的变化图，随着屈服应力的增大，流深也变大。特别是在堆积区倾角为6°时的斜面内，随着屈服应力的增大，流深变大的尤为明显，但是通过与图3 对比可以得知，流深的变化更依赖于黏性系数的变化。

图8为堆积区不同屈服应力下，冲击力和堆积面积的变化图。虽然冲击力与黏性系数呈反比例关系，但是，随着屈服应力的增大，冲击力也随着增大。

图8　冲击力、沉积面积与屈服应力关系图Fig. 8　Impact force and depositional area according to yield stress

图9为FLO-2D模拟下，不同屈服应力状态，泥石流移动范围变化结果图，图9 中，随着屈服应力的增大，倾斜面的运动并没有出现太大的变化，但是堆积区的扩散范围变小。屈服应力愈大，发生初始流动的剪切应力也越大，这使得泥石流在流动过程中会更快停止运动。随着屈服应力的变化，泥石流的沉积特性呈现更大的差异性。由此可知，在影响泥石流发生和停止的因素中，与屈服应力对泥石流流动特性影响相比，屈服应力对堆积特性的影响更大。表4是通过图9 得到堆积区移动特性表，随着屈服应力的变大，堆积距离、堆积宽度、堆积面积不断减小。

表4　泥石流运动特征与屈服应力关系表

4结论

本论文中，利用所收集到的湖北省黄石富水河流域青石沟泥石流的数据，借助FLO-2D数值模拟分析程序，对泥石流的移动特性进行模拟，以此分析泥石流流动及堆积特性与黏性系数和屈服应力的关系，所获得的结论如下：

(1)随着黏性系数的增大，泥石流流速呈非线性减少，流经斜面坡角越大，其变化越大。即：流速同时受黏性系数与流经斜面坡角的影响。斜面坡角对流深的影响不大，但是随着黏性系数的增大，流深也随着增加。黏性系数对泥石流的移动和堆积特性有比较大的影响，与泥石流流速、移动距离、扩散范围呈反比例关系。

(2)屈服应力作为影响泥石流发生及停止的因素，随着屈服应力的增大，流深也随着增大，在泥石流移动特性中，屈服应力对泥石流流速的影响并不明显。随着屈服应力的增加，堆积距离，堆积宽度，堆积面积则减小。由此可知，相比屈服应力对移动特性的影响，屈服应力对堆积特性的影响更大。

(3)随着黏性系数的增加，泥石流冲击力减小，而随着屈服应力的增加，泥石流的冲击力则增大。

参考文献

BertoloLP，WieczorekGF. 2005.CalibrationofnumericalmodelsforsmalldebrisflowsinYosemiteValley，California，USA[J].NaturalHazardsandEarthSystemSciences，5(6)： 993～1001．

HuelimannM，CoponsR，AltimirJ. 2006.DetaileddebrisflowhazardassessmentinAndora：AMultidisciplinarApproach[J].Geomorphology，78(3-4)： 359～372.

ImranJ，HarffP，ParkerG. 2001，Anumericalmodelofsubmarinedebrisflowwithgraphicaluserinterface，Computers&Geosciences，27(6)： 717～729．

Iverson，RM，RiedME，LaHusenRG. 1997.Debris-flowmobilizationfromlandslides[J].AnnualReviewofEarthandPlanetarySciences，25： 85～138．

JohnsonAM，RahnPH. 1970.Mobilizationofdebrisflows[J].ZeitschriftfurGeomorphologie，3(9)： 168～186．

LinML，WangKL，HuangJJ. 2005.Debrisflowrunoffsimulationandverification-casestudyofChen-You-Lanwatershed[J].NaturalHazardsandEarthSystemSciences5(3)： 439～445.

LuoYH. 1998.Methodologicalresearchonnumericalsimulationanddisasterriskassessmentofdebrisflowdepositionfan[D].Wuhan：ChinaUniversityofGeosciences．

O’BrienJS，JulienPY，FullertonWT. 1993.Two-dimensionalwaterfloodandmudfloodsimulation.JournalofHydraulicEngineeringASCE，119(2)： 244～260．

O’BrienJS，JulienPY. 1985.Physicalpropertiesandmechanicsofhyper-concentratedsedimentflows，Proceedingsofthespecialtyconferenceondelineationoflandslide，FlashfloodanddebrisflowhazardinUtah[M].UtahStateUniversity：Utah.260～279．

O’Brien，JS，Julien，PY. 1988. “LaboratoryanalysisofMudflowproperties”.[J]JournalofHydraulicEngineering，114(8)： 877～887.

TangC，LiuXL. 1993.Dynamicsimulationandpredictionmodelofdebrisflow[J].JournalofSoilandWaterConservation，5(3)： 37～40．

TangC.1994a.Numericalsimulationofdebrisflowinundationonthealluvialfansanditspredictionmodeloftheriskareas[J].JournalofsoilandWaterconservation，8(1)： 45～50．

TangC.1994b.Anumericalsimulationstudyontheriskassessmentofdebrisflowaccumulationfan[J].JournalofCatastrophology，9(4)： 7～13．

TangC.1994c.Discussiononnumericalsimulationmethodofplanetwo-dimensionaldebrisflow[J].HydrogeologyandEnginee-ringGeology，21(5)： 9～12.

WuYH，LiuKF，ChenYC， 2013.ComparisonbetweenFLO-2DandDebris-2Dontheapplicationofassessmentofgranulardebrisflowhazardswithcasestudy.[J].JournalofMountainScience，10(2)： 293～304.

ZhangP，MaJZ，ShuHP，WangG. 2014.NumericalsimulationoferosionanddepositiondebrisflowbasedonFLO-2DModel[J].JournalofLanzhouUniversity(NaturalSciences)，50(3)： 363～368．

罗元华. 1998. 泥石流堆积数值模拟及泥石流灾害风险评估方法研究[D]. 武汉：中国地质大学．

石川芳治，水山高久，井户清尾. 1991. 堆积扇上泥石流堆积泛滥机理[M]. 泥石流及洪水灾害防御国际学术讨论会文集. 成都： 27～31．

唐川，刘希林. 1993. 泥石流动力堆积模拟和危险范围预测模型[J]. 水土保持学报，5(3)： 37～40．

唐川. 1994. 泥石流堆积泛滥过程的数值模拟及其危险范围预测模型的研究[J]. 水土保持学报，8(1)： 45～50.

唐川. 1994. 泥石流堆积扇危险度分区评价的数值模拟研究[J]. 灾害学，9(4)： 7～13．

唐川. 1994. 平面二维泥石流数值模拟方法的探讨[J]. 水文地质工程地质.21(5)： 9～12．

张鹏，马金珠，舒和平，等， 2014. 基于FLO-2D模型的泥石流运动冲淤数值模拟[J]. 兰州大学学报(自然科学版).50(3)： 363～368.

RESEARCHONTHEINFLUENCEFACTORSOFFLOWANDDEPOSITIONOFDEBRISFLOWBASEDONTHEFLO-2DSIMULATION

LIANGHongxiSHANGMinXUXin

(College of Civil Engineering & Architecture，China Three Gorges University，Yichang 443002)

AbstractDebris flow is different from the common landslide. It is a kind of temporary water with sand and stones occurred in a mountainous area. As researches shown, the debris flow is characterized with the nature of Bingham Body and moving jams. Many scholars had made many researches of numerical simulation method, which based on rheology experiment and model. And compared the scope, movement speed and movement time of the debris flow with the actual situation, the numerical simulation programs were developed for the forecast of debris flow. The FLO-2D is one of the software. As engineering practice proved, movement and sedimentary characteristics of debris flow is very important for further study based on the flow characteristics of research on debris flow substance composition. In order to analyze the relationship between debris flow movement-accumulation characteristics and viscosity-yield stress, we simulated the moving characteristics of debris flow by FLO-2D model. Through the analysis, we conclude that debris flow velocity is reduced with the increase of the viscosity, and the reduction is nonlinear. With the increase of yield stress, that is one of the impact factors about debris flow occurrence and stop, flow depth increases. But among the debris flow movement characteristics, the effect between yield stress and debris flow velocity is not obvious. With the increase of the viscosity, the impact force of debris flow decreases. Meanwhile, with the increase of the yield stress, the impact force of debris flow is increased．

Key wordsNumerical simulation, FLO-2D,Viscosity, Yield stress

DOI:10.13544/j.cnki.jeg.2016.02.008

* 收稿日期：2015-01-30; 收到修改稿日期： 2015-05-05.

基金项目：梁鸿熙(1991-)，男，硕士生，土木与建筑学院地质工程专业. Email： 421486282@qq.com.

第一作者简介：尚敏(1977-)，男，博士，副教授，主要从事地质灾害机理与防治研究. Email：summing@126.com

中图分类号：P642.23

文献标识码：A