几种重要FHE加密结构的深入研究与分析*

2016-07-05马飞，李娟

通信技术 2016年4期

关键词：云计算

马　飞，李　娟

(1．北方民族大学计算机科学与工程学院，宁夏银川 750021;2．合肥工业大学计算机与信息学院，安徽合肥 230009)

几种重要FHE加密结构的深入研究与分析*

马飞1,2，李娟1

(1．北方民族大学计算机科学与工程学院，宁夏银川 750021;2．合肥工业大学计算机与信息学院，安徽合肥 230009)

摘要：对当前几种重要的全同态加密结构的构造原理及性质进行了深入剖析，重点对FHE加解密算法、算法基于的难题假设、算法复杂度、密钥特征、密文扩展性等特点进行了深入分析与详细比较，并针对结构中的不足之处提出了改进与优化建议，为进一步对FHE结构优化提供借鉴。最后对全同态加密的应用前景进行了全面展望。

关键词：全同态加密；结构比较；云计算；LWE/RLWE

0引言

Rivest等人在上世纪70年代末引入了称为“隐私同态”的概念[1]，在该加密结构的构想下，能允许在密文域中做任意操作，而无需进行解密。随后的研究人员提出了一些操作受限的称之为“半同态”的加密结构，如RSA加密算法[2]与ElGamal加密算法[3-4]是具有任意次乘法运算的乘法同态性加密结构，而其加法运算不具有同态性。Paillier算法[5]与Bresson 等人提出的加密算法具有加法同态性，不具有乘法同态性。而Boneh-Goh-Nissim加密算法[6]支持任意次数的加法运算，但只持一次乘法运算，该算法是最接近于全同态的加密结构之一。直到2009年，IBM公司的Graig Gentry在欧密会上发表了一篇名为《基于理想格的全同态加密》的文章，这一被命名为“全同态加密”(Fully Homomorphic Encryption,FHE)的技术被冠以密码学“圣杯”的称号，成为了密码学最新的研究热点。之后，研究者又在Gentry基础之上提出了一些各有特点的重要的全同态加密方案。本文就几种重要的具有代表性的全同态加密结构进行深入剖析，对它们的特点进行详细比较，并且提出相应的优化建议，为设计新的FHE方案提供一定的借鉴。

1全同态加密及LWE/RLWE难题假设

1.1全同态加密

令P为明文空间，并定义其上有“+”和“×”两种运算，令C为密文空间，在其上定义“⊕”和“⊗”两种运算，E(p)为加密操作，D(c)为解密操作。当公钥加密系统具有全同态性，当且仅当：

∀a,b∈P，D(E(a)⊕E(b))=a+b

(1)

D(E(a)⊗E(b))=a×b

(2)

对于同态评价函数f与g，g:Pn→P,和f:Cn→C，有下式成立：

D(f(c1,…,cn))=g(p1,…pn)，ci=E(pi)

(3)

式中，g由运算“+”和“×”构成，而f由“⊕”和“⊗”两种运算构成。在全同态加密方案中要求在密文上可直接做任意多次相应运算，然后对结果进行解密，其结果为在对应的明文上进行相应的操作而产生的结果。

1.2LWE与RLWE难题假设

本文所分析的五种全同态加密结构都是基于著名的LWE[7]或RLWE难题假设[8]。

LWE难题假设是机器学习中“奇偶性学习问题”的一般化，由Regev首次提出的，并将它应用到公钥加密方案构造中。

1.2.1LWE(Learning With Errors)

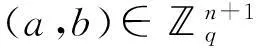
LWEn,q,x问题：从分布χ中取出一些样本，不能近似估计出S的值。

Regev使用量子归约算法证明在一般情况下，只要选择正确的参数n、q和χ，LWEn,q,x问题和最坏情况下任意n维格上的SVP(Shortest Vector Problem)问题和SIVP(Shortest Independent Vector Problem)问题的困难性等价[7]。

1.2.2RLWE(Ring Learning with Errors)

设λ为安全参数，并且f(x)=xd+1且，d=d(λ)，幂为2。令q=q(λ)≥2是一整数。并且满足q≡1modd。令R=[x]/(f(x))和Rq=R/qR。最后令χ=χ(λ)为环R上的误差分布。RLWEd,q,x难题假设可以区分以下两个分布：

1.2.3LWE与RLWE

2重要全同态加密结构剖析

2.1基于理想格的Gentry结构

Gentry方案[9]是构建在环的“理想”概念上。

假设环为R，该环上的一个“理想”为I。运算过程中产生的噪声被定义在I上，即：e=rI，其中r∈R，对m加密：C=m+rI，而解密过程是去掉噪音rI理想的过程。而该结构具有的同态性质：

其中，c1=m1+r1I，c2=m2+r2I。

c1+c2=(m1+m2)+(r1+r2)I

(4)

c1c2=(m1+r1I)(m2+r1I)=

(m1m2)+(m1r2+m2r1+r1r2I)I

(5)

由式(4)和式(5)可知，当进行加法运算时，噪声为(r1+r2)I，乘法运算时，噪声主要由r1r2I产生。做加法运算时噪音是倍加，做乘法运算时，噪音以平方的形式增加，随着运算次数不断增加，噪音将变的很大时将产生译码错误。而Gentry结构中是采用叫做“评价同态解密函数”来处理，该函数是以具有噪音的密文作为输入，而其输出是一个具有小噪音的一个密文，而对噪音不超过阀值的密文可以正确解密。

Gentry结构依赖于基于理想格的困难性假设，而其不足之处在于现在对于理想格域的研究还不是非常完善，并且该结构需要十分有效的压缩步骤去减小译码的复杂度。除了基于理想格的困难假设外，该结构还需要一个基于“松散子集和”的假设。虽然Gentry结构只是一种理论化的模型，但由于它是第一个被证明为全同态的加密结构，所以具有很重要的现实意义，在其基础上出现了一些结构更加优化并且也具有全同态性的加密结构。

2.2Brakerski和Vaikuntanathan结构

简称为BV结构，BV结构[10]比之于Gentry结构的一个显著不同之处在于使用了著名的DLWE安全假设，并且引入了“再线性化”和“模转换”技术[9]，而模转换技术的出现可去掉在Gentry结构中出现的复杂的压缩过程并且可以有效的对噪声进行控制。结构的“自举性”使其很容易构造成全同态结构。该方案基于LWE假设，其结构如下：

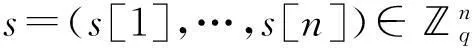
假设要加密比特m∈{0,1}，首先随机选择r∈{0,1}k，然后计算:

a=ATr，b=vTr+m

(6)

最后输出(a,b)。为解密密文(a,b)，先计算：

b′=b-〈a,s〉=2e+m∈q

(7)

式中，e为噪声，〈a,s〉为内积计算，最后输出：

m=b′ mod 2

(8)

2.3Brakerski和Gentry, Vaikuntanatuhan结构

该结构简称为BGV结构[11]，BGV结构是基于环[x]/(f(x))，f(x)为次n的不可约多项式，且Rq=R/qR，q为一个素数模。另外一个参数是基于环R的错误分布χ。BGV结构与BV结构相比，其显著的扩展是使用了RLWE假设，而该假设对提高同态加密结构的加密效率做出了很大的贡献，而且由于仔细使用了 “模转换”技术使得可以去掉在Gentry方案中提出的“自举”过程而获得“全同态”性质，从而提高了该结构的工作效率。

在该结构中既可以使用LWE假设，也可以使用RLWE假设，本文分析的是效率更高的基于RLWE难题假设的结构方案。该结构可描述如下：

选择λ作为安全参数，另一个参数为μ，首先选择一个μ比特去计算modq。然后选择d=d(λ,μ)，χ=χ(λ,μ)，n=「3logq⎤。令Rq=q[x]/(f(x))。为获得私钥，从分布χ中均匀取出S′，私钥则为：

(9)

(10)

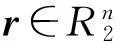
(11)

根据RLWEd,q,x问题假设(此处的χ为基于Rq的均匀分布)，在此结构下，攻击者在多项式时间里猜测出的S的概率可以忽略为0。对于解密而言，只需计算b′=[〈c,s〉]q，然后输出m=[b′]2。

2.4Brakerski结构

Brakerski结构[12](Bra结构)使用了与Regevs相似的基于LWE的公钥加密结构。其加密结构可描述为：

给定一个安全参数n，令q=q(n)为一个整数。而χ=χ(n)是基于整数集的一个分布。令私钥为。

为取得公钥，令：N=(n+1)·(logq+ο(1))并且A←N×n，e←χN。计算b=[A·s+e]q，而公钥为：P=[b|-A]∈N×(n+1)。假设要加密密文：m∈{0,1}，可首先随机选择一个r∈{0,1}N，设m=(m,0,…,0)∈{0,1}n+1，最后输出的密文为。而解密c，可先计算c0=[〈c,(1,s)〉]q，则明文为m=[「2·c0/q」]2。

2.5Fan和Vercauteren结构

Fan和Vercauteren结构[13](FV结构)，该结构使用了经过修改后的基于RLWE问题的LPR结构，在效率上比之于使用LWE假设的Bra结构有了进一步的提高，由于它包含了一个经过修改后的LPR结构，使得结构更容易优化与分析。

(12)

a取自于Rq。假设对m∈Rt进行加密，从分布χ中取出r，e1，e2。然后计算：

u=a·r+e1+Δ·mmodq

(13)

v=b·r+e2modq

(14)

返回(u,v)。而解密时，首先计算下式：

u+v·s=(r·e-s·e1+e2)+Δ·mmodq

(15)

然后去乘t/q，然后把结果值取整再与t取模。

3FHE结构特征与性能比较和分析

3.1FHE结构性能比较

(1)对于“BV结构”，按其构造原理分析得到：其公钥尺寸为O(n2log2q)，私钥尺寸为nlogq，密文尺寸为(n+1)logq，基于的数学难题为LWE。

(2)对于“FV结构”，按其构造原理分析得到：其公钥尺寸为2dlogq，而私钥尺寸为d，密文尺寸为2dlogq，基于的难题假设为RLWE。

(3)对于“Bra结构”，按其构造原理分析得到：其公钥尺寸为O(n2log2q)，私钥尺寸为nlogq，密文尺寸(n+1)logq，基于的难题假设为LWE。

(4)对于“BGV结构”，按其构造原理分析得到：其公钥尺寸为2dnlogq，私钥尺寸为2dlogq，密文尺寸2dlogq，基于的难题假设为LWE或RLWE。

根据这几种FHE结构的公钥尺寸、私钥尺寸、密文尺寸以及基于的难题假设这几个特征可以看到，当加密方案采用相同的难题假设时，结构间的性能，比如密钥的长度和输出密文尺寸都具有一定的相似性。而由于FV结构和BGV结构都采用了RLWE难题假设，所以它们的密钥尺寸和输出的密文尺寸都要小于基于LWE难题假设的BV结构和Bra结构。综合比较，这四种方案中FV的密钥尺寸最小，究其原因在于其对密钥尺寸进行了优化，并且没有采用其它方案经常采用的矩阵形式作为公钥，从而进一步降低了公钥的尺寸。

3.2FHE结构分析

(1)BV结构对Gentry结构的改进主要是针对安全性这一方面而言的，BV结构是基于LWE问题，其安全性要优于基于理想格的Gentry结构。并且，它所采用的“再线性化”技术使其能够保持密文长度基本恒定，并且易于建立“类全同态”结构。而“模转换”技术能对执行同态操作时产生的噪声进行有效的控制，从而不必采用Gentry结构中复杂的压缩步骤。

(2)对于BGV结构而言，它既可以采用LWE难题假设，也可采用RLWE难题假设。在通常情况下，采用的RLWE难题的结构效率要优于BV结构。而同样采用的“模数转换”技术可以比较好的减少噪音，所以该结构也不需要Gentry结构中的“自举”技术，而且比之于BV结构更易于对噪音进行分析。

(3)Bra结构中用到的LWE问题与经典问题GapSVP的困难性一致。在该方案中，噪音不是以乘法平方的形式增大，而只是以固定多项式倍乘的形式增大。该方案中也使用了BGV结构中的密钥转换技术。

(4)在FV结构中把Bra方案中的RLWE应用到了结构设计中，这个结构是本文所讨论的全同态方案中最有效率的，而解密电路也是这几个方案中最简单的。该结构中使用了两种“再线性化”技术来使其具有“类同态”性质。第一种“再线性化”技术和BGV结构中的密钥转换技术类似，而第二种“再线性化”技术与“模转换”技术相似。几种全同态加密结构的主要思想见表1。

表1　几种全同态加密结构的主要思想

3.3改进建议

(1)在BGV结构，一些性能都与扩展因子有关，而通过试验研究，这个扩展因子的值会小于一个特定值，若能找到这个特定值或其上界，则可以进一步改善与该扩展因子相关的一些性能界限。

(2)在基于RLWE的BGV结构中，当并行计算评价多个功能函数时，可尝试利用“中国剩余定理”，只用一个比较大的模数来评价一个单独的功能函数，来替代对多个功能函数进行的评估。

以上是针对这几种FHE方案所采取的结构、参数特征、基于的难题假设等方面进行的深入对比与分析。这几个方案都有各自的特点，但它们都有一个共同的问题：效率比较低。因为它们都具有高的算法复杂度，庞大的密钥尺寸等问题，使得目前的这些全同态加密结构在实用性方面还不尽如人意。所以研究者在不断优化FHE加密结构的同时，也提出了一些所谓有限全同态加密结构，即“类同态”结构。该结构可支持多次加法，一定量次的乘法运算，而这些“类同态”结构相对于全同态加密结构而言具有算法复杂度小的特点，在不要求全同态的应用领域有更多的实践意义，这也是全同态结构在完全实用化之前可选的一种折衷方案。所以，全同态加密下一步的研究工作就是实用化，而这要求研究者继续寻找更加优良的加密结构。

4FHE应用展望

(1)全同态加密领域的突破性进展为云计算和物联网的发展带来了新的契机，而云计算中数据安全和隐私保护是云计算发展的关键，将直接影响人们对云计算的接受程度。全同态加密有助于推动云计算和物联网的普及和应用，使其为更多的企业、用户认知和接纳。

(2)全同态加密为云计算和物联网的数据安全和隐私保护提供了全新的思路，使得对存储在云端服务器中的加密数据进行运算和操作成为可能，不仅极大地减少了云端服务器和用户的通信及计算开销，也保证了数据处理过程中的安全性。

(3)利用全同态加密技术，在保护用户数据隐私性的同时，为分析和挖掘云服务商CSP(Cloud Service Provider) 所存储的海量数据开辟了无限的商机。目前的全同态加密方案计算量巨大，难以在现有计算技术条件下实现。如何提高全同态加密方案的加解密效率、降低密钥存储空间，都是当前的研究难点。

5结语

本文重点对当前几种重要的全同态加密结构：Gentry结构、BV结构、BGV结构、Bra结构和FV结构的构造过程及各自具有的特性进行了深入的剖析。着重从几种方案的加解密算法结构、算法基于的难题假设、算法的复杂度、密钥特征、密文扩展性等特点进行了深入分析与详细比较。从分析与比较结果看，在安全性方面，基于理想格的Gentry结构弱于基于LWE或RLWE的其它几种结构。在结构的性能比较上，FV结构的灵活性及方案效率是优于其它几种结构。文章最后还针对几种结构中的不足之处提出了改进与优化建议，为FHE进一步进行结构优化提供了一定的借鉴。

参考文献：

[1]Ronald L. Rivest, Leonard M. Adleman, Dertouzos M L. On Data Banks and Privacy Homomorphisms[J]. Foundations of Secure Computation,1978,4(11):169-180.

[2]Ronald L. Rivest, Adi Shamir, Leonard M. Adleman. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120-126.

[3]Taher ElGamal. A Public Key Cryptosystem and A Signature Scheme based on Discrete Logarithms[C] //Advances in Cryptology. Springer Berlin Heidelberg, 1984: 10-18.

[4]白永祥.一种高效群签名方案的设计与分析[J]. 通信技术,2015,48 (02):214-218.

BAI Yong-xiang. Design and Analysis of Efficient Group-Signature Scheme[J]. Communications Technology, 2015,Vol 48 (2):214-218

[5]Pascal Paillier. Public-Key Cryptosystems based on Composite Degree Residuosity Classes[C]// Advances in cryptology—EUROCRYPT’99. Springer Berlin Heidelberg, 1999: 223-238.

[6]Dan Boneh, Eu-Jin Goh, Kobbi Nissim. Evaluating 2-DNF Formulas on CipherTexts[M]//Theory of Cryptography. Springer Berlin Heidelberg, 2005:325-341.

[7]Oded Regev. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography[J]. Journal of the ACM (JACM),2009,56(6):34.

[8]Zvika Brakerski, Vinod Vaikuntanathan. Fully Homomorphic Encryption from Ring-LWE and Security for Key Dependent Messages[M]//Advances in Cryptology-CRYPTO 2011. Springer Berlin Heidelberg,2011:505-524.

[9]Craig Gentry. Fully Homomorphic Encryption using Ideal Lattices[C]//STOC(Proceedings of the Forty-first Annual ACM Symposium on Theory of Computing), New York. 2009, 9: 169-178.

[10]Zvika Brakerski, Vinod Vaikuntanathan. Efficient Fully Homomorphic Encryption from (Standard) LWE [J]. SIAM Journal on Computing, 2014, 43(2): 831-871.

[11]Zvika Brakerski, Craig Gentry, Vinod Vaikuntanathan. (Leveled) Fully Homomorphic Encryption without Bootstrapping[J]. ACM Transactions on Computation Theory, 2014, 6(3): 169-178.

[12]Zvika Brakerski. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP[M]//Advances in Cryptology-CRYPTO 2012. Springer Berlin Heidelberg, 2013: 868-886.

[13]FAN Jun-feng, Federik, Vercauteren. Somewhat Practical Fully Homomorphic Encryption[C] //Crypto Cambridge, UK ,2013:247-249.

Research and Analysis of Several Key FHE Structures

MA Fei1,2, LI Juan1

(1.School of Computer Science and Engineering, Beifang University of Nationalities,Yinchuan Ningxia 750021,China;2.School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009,China)

Abstract：In-depth study on principles and properties of the current most important FHE (Fully Homomorphic Encryption) structures is done,with focus on analysis and comparison of FHE encryption and decryption, algorithm based on hard problem, algorithm complexity, key characteristics and ciphertext expansion. In light of the deficiencies, some modified and optimized solutions are presented, and these could serve as a reference for further optimization of FHE structure. Finally, application prospects of FHE are forecasted.

Key words：FHE; structure comparison; cloud computing; LWE/RLWE

doi:10.3969/j.issn.1002-0802.2016.04.019

*收稿日期：2015-11-17；修回日期：2016-03-05Received date:2015-11-17；Revised date：2016-03-05

基金项目：获得宁夏回族自治区‘计算机应用技术’重点学科项目资助；宁夏教育厅“十三五”自治区重点专业——网络工程专业重点建设项目资助

Foundation Item:Key Discipline Project (Computer Application Technology) of Ningxia;Foundation Project( Priority Majors of Network Engineering ) of the Education Department of Ningxia in the 13th Five-Year Plan

中图分类号：TN918.4

文献标志码：A

文章编号：1002-0802(2016)04-0481-05

作者简介：