基于运动学约束的移动车辆捷联惯导定位方法及实验研究*

司卓印，李　威，杨　海，张金尧

(中国矿业大学 机电工程学院，江苏 徐州　221116)

基于运动学约束的移动车辆捷联惯导定位方法及实验研究*

司卓印，李威，杨海，张金尧

(中国矿业大学 机电工程学院，江苏 徐州221116)

摘要：针对移动车辆捷联惯性导航系统中长时间存在累计误差使得系统定位精度较低的问题，利用卡尔曼滤波算法，提出了一种基于运动学约束的移动车辆捷联惯性导航算法。该算法利用车辆运动参数信息构建状态方程，同时根据车辆运动过程中的运动学约束来构建速度观测方程，并搭建实验平台进行实验验证。实验结果表明，该方法能够有效抑制捷联惯导定位误差发散现象，x方向和y方向的位置误差分别为0.0328m和-0.049m，相对于传统解算方法定位精度分别提高了84.8%和88.9%，能够准确得到移动车辆的位置信息。

关键词：移动车辆；捷联惯性导航；运动学约束；卡尔曼滤波

0引言

随着工业自动化技术的发展，移动车辆定位技术受到越来越多的关注，其应用领域和范围也在不断的扩展，在面对一些较复杂的任务时，如工厂搬运车辆的智能监控、军事移动装备定位、救援机器人等，定位技术发挥着越来越重要的作用。由于应用环境的特殊性存在诸多未知因素，对定位技术提出了更高的要求。目前移动车辆定位技术主要有捷联惯性导航系统(Strap down Inertial Navigation System，SINS)[1]、全球定位系统(Global positioning systems,GPS)[2]、无线传感器网络(Wireless Sensors Network,WSN)[3-4]、红外线定位技术[5]、视觉定位技术[6]等。

现如今对移动车辆进行定位的主要技术是GPS定位，但GPS无法在室内和建筑物密集区域使用；而红外线定位技术只能在直线视距内应用，其传输距离较短，且容易受外界环境的干扰，局限性比较大；捷联惯性导航系统不依赖任何外界信息，也不向外发射信息，利用测量载体自身的加速度和角速度信息，通过四元数法解算来实时获取载体位姿信息[7]，具有短时间高精度，数据更新率高，可实现自主定位导航等特点。然而惯性导航在长时间工作过程中不可避免地存在固有的累积误差，从而导致测量精度严重下降。针对这一缺陷，文献[8]提出对移动车辆进行间歇停车操作，利用停车时刻的真实速度为零对惯性导航系统中的误差进行辨识和补偿，但是这种校正方法必须进行停车，不能够满足实际工况要求。

针对上述问题，本文提出一种基于运动学约束的捷联惯性导航车辆定位算法。利用移动车辆位置和速度建立系统状态方程，通过其运动过程中车体横向及天向的速度分量为0的运动学约束特性来建立观测方程，运用卡尔曼滤波算法对状态空间方程进行滤波，并搭建捷联惯导移动车辆定位实验平台，实现对移动车辆定位算法的实验验证。

1移动车辆的定位解算模型

捷联惯性导航系统数字算法是以迭代递推的形式表示，即采用系统微分方程组的形式进行描述，将移动车辆过去前一时刻的导航信息和此时刻的惯性器件的采样值作为输入值，通过逐次递推计算出当前时刻的导航信息。

移动车辆姿态更新的四元数微分方程为[9]：

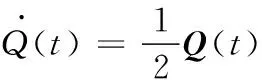
(1)

(2)

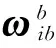
移动车辆速度更新的微分方程为[10]：

(3)

其中：fb是加速度计测量的比力；gn为重力加速度矢量。

移动车辆位置更新的微分方程为：

(4)

其中L，λ，h分别为移动车辆所在位置的纬度，经度和高度。vx，vy，vz分别为移动车辆在导航坐标系下的速度分量，RM，RN分别为当地子午圈半径和卯酉圈半径。对式(4)积分即得到其所在位置的纬度、经度和高度。

2系统定位数学模型建立

本文主要针对SINS移动车辆定位系统中定位误差随时间累积的问题，提出的基于运动学约束的卡尔曼滤波误差补偿模型，如图1所示。惯性导航系统固定安装在移动车辆上，实时测量移动车辆的三轴加速度和三轴角速度，并且通过惯性导航四元数解算模型实时解算出其位置和姿态信息，建立系统状态方程。根据运动学约束特性建立观测方程，并进行卡尔曼滤波，实现对捷联惯导定位误差的矫正。

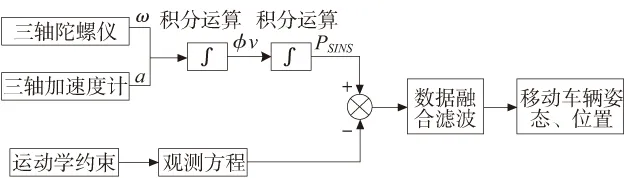
图1　导航定位系统原理框图

2.1运动学约束模型建立

移动车辆的载体坐标系为b系，Yb轴指向车辆行驶正前方，Xb轴指向右侧，Zb轴竖直向上，并规定导航坐标系下Xn、Yn、Zn轴的指向依次为东、北、天，其运动学模型如图2所示。移动车辆运动学约束条件是指当车辆在水平面正常行驶过程中，如果没有发生跳跃和侧滑，则在b系中Xb轴速度、Zb轴速度分量为零，即：

(5)

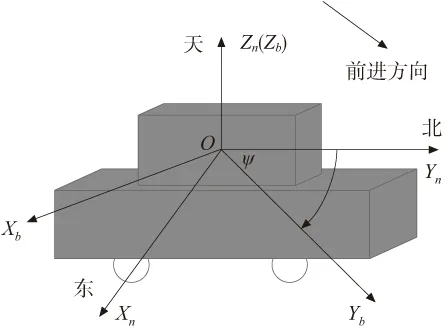
图2　移动车辆运动学模型示意图

2.2系统状态方程

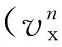
xk=Φk,k-1xk-1+Bk,k-1Uk-1+Γk,k-1ωk-1

(6)

Bk,k-1为系统的控制输入矩阵，定义为：

(7)

(8)

其中k为系统的采样周期计数，T为采样周期。Γk,k-1为系统转移干扰矩阵，在该系统设为单位阵。ωk为状态方程的系统噪声，其向量形式表示为：

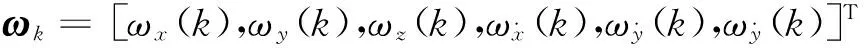
其统计特性为：E[ωk]=0，Rωω(k,j)=Qkδkj，Qk为系统噪声的协方差。B1可定义为：

2.3系统观测方程

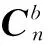
(9)

从而得到车体坐标系b系中的速度分量为：

(10)

zk=Hkxk+υk

(11)

Hk=H1H2

(12)

2.4卡尔曼滤波算法

通过上面的推导可以建立系统状态空间方程：

(13)

根据卡尔曼滤波的原理[11]，卡尔曼滤波算法流程如下：

(1)状态量的初步更新预测：

(14)

(2)误差协方差的更新预测：

(15)

(3)状态估计矫正：

(16)

(4)求卡尔曼增益：

(17)

(5)误差协方差矩阵的更新：

Pk|k=[I-KkHk]Pk|k-1

(18)

上述过程即为卡尔曼滤波的实现步骤，滤波器每次执行都按此过程循环。

经过卡尔曼滤波之后，就能得到导航坐标系下k时刻移动车辆的位置最优解和速度最优解，再次通过系统模型方程(13)便可得到移动车辆k+1时刻移动车辆的位置和速度信息。

3实验验证

为了验证本文所提出的运动学约束条件下卡尔曼滤波算法对移动车辆导航系统的定位性能，搭建如图3所示的移动车辆定位实验平台进行实验验证。通过四元数位姿解算方法与运动学约束条件下卡尔曼滤波算法分别对移动车辆的轨迹进行跟踪。

1.上位机 2.移动车辆 3.捷联惯性导航 4.遥控操作器 5.无线蓝牙模块

图3移动车辆实验平台

3.1实验准备及参数设定

实验选用型号为IMU800CA-200捷联惯性导航，其中陀螺计零偏稳定性为0.025(°/h)，加速度计零偏稳定性为0.15mg，其融合了先进的MEMS速率陀螺技术，具有优异的可靠性和稳定性；选用无线蓝牙模块，能够将SINS的数据与上位机实现实时通信，波特率为115200bit/s，从而实现对移动车辆运动轨迹的实时校正；选用基于Arduino可编程无线控制器，实现对移动车辆运动的实时控制；移动车辆装备4路红外循迹模块，实现对移动车辆真实轨迹的测量标定。

3.2移动车辆位置跟踪实验

初始时刻，通过初始设定，使得移动车辆的载体坐标系和导航坐标系完全重合，且车辆相对捷联惯导安装偏差角为一个可忽略的小角度范围，从而实现惯性导航与移动车辆的初始对准。实验初始位置为x0=(0 0 0)m；初始速度为v0=(0 0 0)m/s；初始姿态角为ψ=0°，θ=0°，γ=0°；实验采集3000个采样点，采样周期为0.01s。本实验移动车辆行走的轨迹如图4所示，分为下面五个阶段：第一段直线OA—第一次拐弯(偏航角为-40.73°)—第二段直线AB—第二次拐弯(偏航角为43.97°)—第三段直线BC。

图4　移动车辆行走轨迹

利用捷联惯性导航装置测量出移动车辆实时运行状态下的姿态角和加速度信息，并根据四元数法解算出移动车辆在运行过程中的SINS跟踪轨迹信息，并与运动学约束下的卡尔曼滤波后的轨迹作对比，并且根据设置好的基准参考轨迹，计算出移动车辆的定位误差，得到此算法下移动车辆捷联惯导系统的定位精度。

从图5中可以看出卡尔曼滤波下的定位导航系统在第一次转弯处出现较大的定位误差这是因为在转弯时速度方向变化较大；而SINS跟踪轨迹在移动车辆行走第一段直线时和真实轨迹相吻合，这主要是因为SINS系统在短时间内能够实现高精度定位。

图5　移动车辆轨迹对比图

在小车行走到第二段直线时，卡尔曼滤波下的定位导航系统能够很好地跟踪移动车辆的真实轨迹，然而SINS跟踪轨迹在此阶段由于累计误差导致定位精度有所下降，位置误差为0.46m。

移动车辆在第二次转弯时，由于小车的速度波动，导致卡尔曼滤波下的定位导航系统在短时间出现波动现象，而此后能够很好地跟踪小车的真实轨迹，直至小车停止；此阶段由于SINS累积误差的影响，导致定位精度严重下降，无法满足定位要求。

卡尔曼滤波定位导航系统的位置误差曲线如图6所示，在x方向和y方向(移动车辆前进方向)上均有误差，最大相对误差分别为-0.11m和0.26m，且在两次转弯过程中明显看出相对误差波动性比较大，这主要是因为转弯时速度方向变化较大。而在小车运行到终点的过程中均保持较高定位精度，到达终点时x方向和y方向上的相对误差分别为0.0328m和-0.049m，满足实际的工程要求。

纯SINS定位位置误差曲线如图7所示，起始阶段定位精度高，随着时间累积，定位精度严重下降，在x方向和y方向最大相对误差为0.85m和-1.98m。图6和图7对比可以看出采用运动学约束下的卡尔曼滤波定位系统具有很好的误差收敛能力，虽然在定位初期和噪声变化下产生两个误差峰值，但定位误差快速稳定下来，定位精度明显优于纯SINS导航定位系统。在x方向和y方向上较纯SINS解算的定位误差分别减少84.8%和88.9%。引入运动学束条件下的卡尔曼滤波算法有效地抑制了纯SINS误差随时间积累而发散的现象，使得SINS能够很好地跟踪移动车辆的真实轨迹，且能满足SINS移动车辆系统长时间的导航要求，是一种可行的定位滤波算法。

图6　卡尔曼滤波定位导航系统的位置误差曲线

图7　纯SINS定位位置误差曲线

4结束语

针对移动车辆纯SINS定位系统长时间运行时存在累积误差导致位置发散的问题，本文提出一种基于速度的运动学约束条件下的卡尔曼滤波算法，并且在智能移动小车上搭建了捷联惯导定位实验平台。实验结果表明，该算法的定位精度相对于纯捷联惯导解算模型，在x方向和y方向上分别提高84.8%和88.9%，并且提高了SINS自主导航的持续性和稳定性。本文的研究算法对提高导航系统的定位性能和应用有一定的指导意义。

该辅助算法可用于SINS/GPS组合导航系统中，用于当GPS失效时，实时提高纯SINS的定位精度，改善SINS/GPS移动车辆导航系统的导航精度，提高定位系统的可持续性。

[参考文献]

[1] Fan Qigao, Li Wei,Luo Chengming.Error analysis and reduction for shearer positioning using the strapdown inertial navigation system[J].International Journal of Computer Science Issues,2012,9(5):49-54.

[2] Mohinder S Grewal,Lawrence R Weill,Augus P Andrews,et al.GPS惯性导航组合[M].陈军,易翔,梁高波,等,译.2版.北京：电子工业出版社,2011.

[3] 王小平,罗军,沈昌祥.无线传感器网络定位理论和算法[J].计算机研究与发展,2011,48(3):353-363.

[4] 邓琛,王永琦.基于模糊控制的无线传感器网络室内定位算法[J].计算机应用,2011,31(8):2062-2064.

[5] 燕学智,王树勋,马中胜,等.基于超声红外定位导航研制自动引导车辆系统[J].吉林大学学报：工学版,2006,36(2):242-246.

[6] Li J Y, Yang C,Wang J,et al.A Robot Handling System Based on Visual Orientation[J].Manufacturing Automation, 2011.33(2):40-42.

[7] 秦永元.惯性导航[M].2版.北京：科学出版社,2014.

[8] Park SK,SuhY S.A zero velocity detection algorithm using inertial sensors for pedestrian navigation systems.[J].Sensors,2010,10(10):9163-9178.

[9] 马韬,陈杰,陈文颉.对偶四元数捷联惯性导航系统初始对准方法[J].北京理工大学学报,2012,32(1):56-61.

[10] 魏纪林.高动态下激光捷联惯导系统算法研究与实现[D].哈尔滨：哈尔滨工业大学,2012.

[11] 袁亮,楚仕彬.基于卡尔曼滤波的无人机姿态测量研究[J].组合机床与自动化加工技术,2015(7):110-113.

(编辑赵蓉)

Experimental Study on SINS Positioning Technology for Mobile Vehicle Based on Kinematics Constraint

SI Zhuo-yin，LI Wei，YANG Hai，ZHANG Jin-yao

(School of Mechatronic Engineering,China University of Mining and Technology,Xuzhou Jiangsu 221116,China)

Abstract：A solution method for mobile vehicle based on kinematics constraint using Kalman filter(KF) is proposed to solve the problem of low positioning accuracy of mobile vehicle in terms of SINS(Strap down Inertial Navigation System)existing the cumulative error with long-term.The state equation of KF is constructed by the mobile vehicle parameters information and the observation equation of velocity is constructed by the process of the kinematics constraint.Meanwhile,the test platform is constructed for the experiment.Results indicate that this method can restrain effectively the position error divergence of the SINS.The position error of mobile vehicle is 0.0328m and -0.049m in x and y direction respectively.Compared with the traditional method,the position accuracy improves 84.8% and 88.9% respectively,which means that the solution method for mobile vehicle based on kinematics constraint using KF can track the position effectively

Key words：mobile vehicle；strap down inertial navigation system(SINS)；kinematics constraint；kalman filter

文章编号：1001-2265(2016)06-0063-04

DOI:10.13462/j.cnki.mmtamt.2016.06.016

收稿日期：2015-12-14;修回日期：2016-01-11

*基金项目：国家高技术研究发展计划(863)资助项目(2013AA06A411)；江苏省“333工程”科研资助项目(BRA2015300)；江苏省研究生培养创新工程资助项目(KYLX_1374)

作者简介：司卓印(1990—)，男，江苏徐州人，中国矿业大学研究生，研究方向为移动装备组合定位技术，(E-mail)szy900820@163.com。

中图分类号：TH166;TG659

文献标识码：A