基于温度分布的烤盘形状最优化分析

黄嘉欣

（华南师范大学数学科学学院，广东广州510631）

基于温度分布的烤盘形状最优化分析

黄嘉欣

（华南师范大学数学科学学院，广东广州510631）

摘要：通过探究烤盘形状对烤箱空间利用率和受热烤盘温度分布的影响，分析矩形烤盘四角容易烤焦食物的原因，结合实际和假设条件提出优化模型，设计出最优的烤盘，并对上述模型进行测试和评价.在模型测试中，给出了在p改变时的结果；在模型评价中，分析了各个模型的优缺点.

关键词：温度分布；热传导方程；评价函数；参数量化

1　问题重述

随着经济的发展，越来越多的烤箱进入人们的日常生活，烘烤食物成为了最普通的需求之一.人们在使用不同烤盘烘烤食物的时候，会出现不满意的情况，如矩形烤盘四角的食物容易被烤焦、圆形烤盘在烤箱内的空间利用率不高.因此建立烤盘形状最优化模型有着重要的实际意义.

下面建立数学模型来给出可挑选的最佳烤盘形状，并考虑以下情况.

（1）烤箱容纳烤盘数目最大化（N）；

（2）烤盘的均匀受热程度最大化（H）；

（3）优化组合上述两个条件，分别用p和（1-p）来表示其权重分配，随着烤箱形状与p的变化，展示出结果的变化.

在建立优化模型的过程中，将分为以下几个步骤，即：

（1）建立描述不同形状烤盘的热均匀程度的量（即模型1的分析结果）；

（2）选取、确定烤盘摆放方式；

（3）构造组合优化的评价函数.

2　基本假设

（1）烤箱内部温度恒定；

（2）烤盘用导热性能良好且各项同性的介质制成；

（3）烤盘的形状近似为无盖的长方体（或正多边形、圆形）盒子.

3　模型解决

3.1模型1：多边形烤盘温度分布模型

根据热传导理论［1］，一种材料本身或者当与其他材料接触时，产生的能量传递的过程（或效率）也被称为该种材料的导热系数.而热辐射［2］则是另一种可以在没有任何媒介或者接触下产生热量交换的方法，烤箱的加热原理正是利用热辐射的方法［2］，对食物进行加热.

3.1.1模型假设

（1）烤盘内部没有热源；（2）忽略烤盘的厚度.

3.1.2建立模型

基于基本假设中的各向同性条件，恒温箱中烤盘的各个面所接受的热流密度相同，因此，烤盘的温度分布不均匀是烤盘金属材料之间的热传导造成的.根据热传导方程

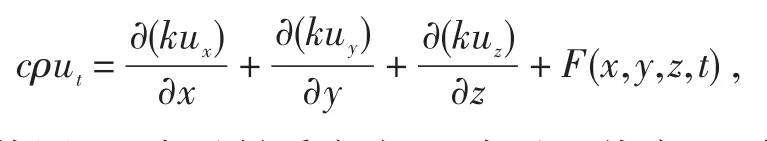
其中：u表示温度；F（x,y,z,t）表示内热源；ρ表示材质密度；c表示比热容；k表示热传导系数.由上式可得无内热源的瞬态热传导方程，即烤盘的瞬态热传导方程：

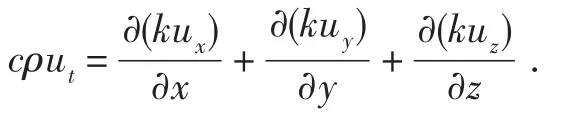
该微分方程的边界条件采用诺曼边界条件［3］，即已知各面的法向热流密度= -k∇u .

如果仅考虑烤盘底面受热，忽略烤盘侧面，则烤盘表面的温度将会平均分布.因此，烤盘温度分布不均主要是侧面接收的热量向底面传导所造成的，故可以将三维热传导模型简化为二维平面热传导模型，其热流示意图如图1所示.

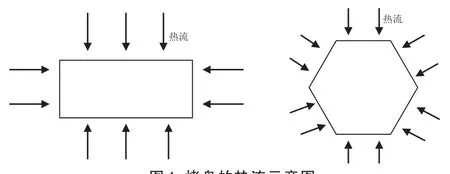
图1　烤盘的热流示意图

二维热传导模型［4］的瞬态解可以利用有限元分析法求解，利用MATLAB提供的PDEtool工具［5］计算，可得二维热传导模型的数值解.

为了对比矩形烤盘及圆形烤盘在上述条件下的温度分布，不妨把烤盘的参数设置如表1所示.计算结果如图2所示.

表1　各项参数设置表

由图2可知，矩形烤盘的四角温度偏高，中心温度最低，边缘的温度变化差异大.而等面积的圆形烤盘则边缘温度均匀，中心温度较低.

现保持烤盘面积不变，将正多边形的边数增加，可以计算烤盘温度方差代表其均匀受热程度，如表2所示.

由表2可见，在面积一定的条件下，圆形烤盘的温度方差比其他形状的烤盘的要小，也就是说圆形烤盘的均匀受热程度最大，使得食物受热最均匀.

随着正多边形边数的增加，受热烤盘整体温度方差逐渐减小.边缘形状不仅影响边缘温度分布，还影响整体温度分布的均匀程度.正多边形的边数越多，整体温度分布也越均匀.因此，可用整体温度分布的方差来衡量受热烤盘温度分布的均匀程度.

3.2模型2：烤盘排布模型

若要使得烤盘数量N排布最多，则必须尽量使用密排布；同时，根据生活实际，对于各种形状的烤盘都可以转化成矩形密排布的方式摆放.

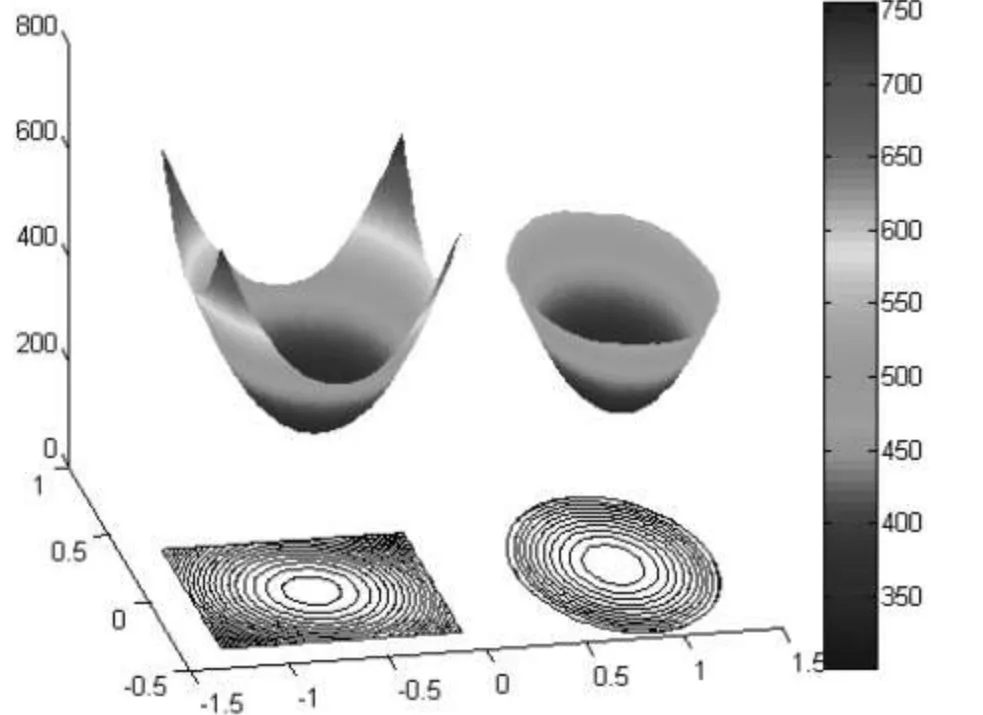
图2　温度分布三维示意图（左为矩形烤盘，右为圆形烤盘）

3.2.1矩形烤盘

根据矩形面积公式，以及给定的烤盘面积A和长宽比B，可以求出矩形的长和宽如下：

现在建立矩形排布模型来获得最终排布图案，其排布草图如图3所示.几何约束条件如下：

由上述分析可知，当仅当烤箱总面积S是每个烤盘面积A的整数倍时，矩形烤盘才能完全密排布.

表2　不同多边形烤盘温度方差表

图3　排布方式草图

按照此模型排布时，将会优先贴近某三边排布，最后将剩余的位置划为（N - nwnl）个面积不同的矩形，如图4所示.

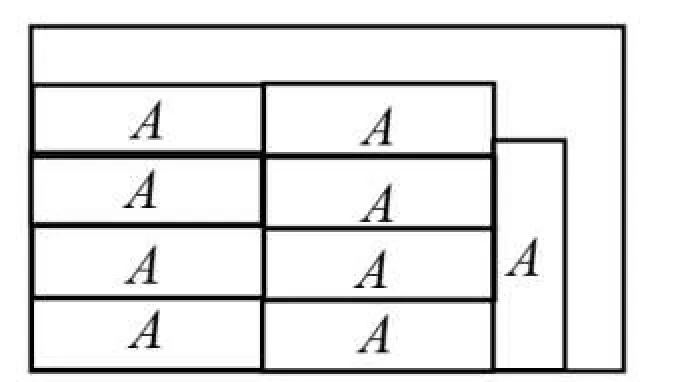
图4　一种矩形排布方式

表3　每个烤盘i及其Ni和Hi

3.2.2正多边形烤盘

考虑烤盘形状是规则的边数为偶数的正多边形，对于每一个这样的正多边形，可以找到与之对应的外接矩形，如图5所示，其长度l和宽度w分别如下：

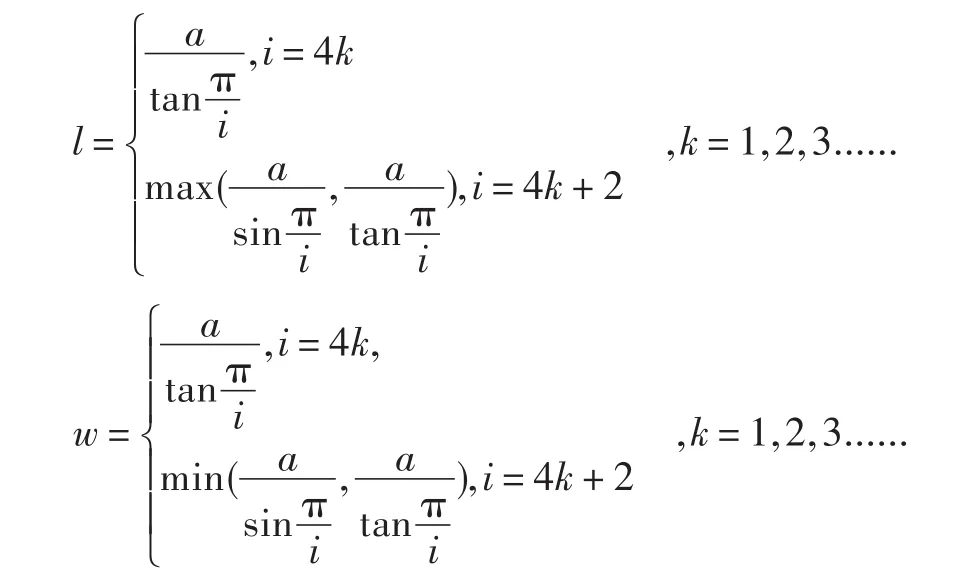
现在，根据实际生活使用习惯，不妨假设正多边形烤盘的排布采用规则排布，即也利用矩形排布模型进行排布.基于矩形烤箱形状与正多边形烤盘形状的差异，可以发现，正多边形的排布不能做到完全紧密排布.其排布草图如图6所示.

3.3模型3：评价目标函数模型

根据模型1和模型2可以求出每个具体形状的烤盘i的Ni和Hi，如表3所示，进而求出其中的最大值，记为Nmax和Hmin.

为了利用评价函数优化结合Ni和Hi，有必要将Ni和Hi作标准化处理.当Ni越大时，说明烤箱内烤盘数目越大，烤箱的利用率越高；当Hi越小时，说明烤盘均匀受热的程度越好，因此，将其标准化处理为和，并建立如下的评价目标函数：

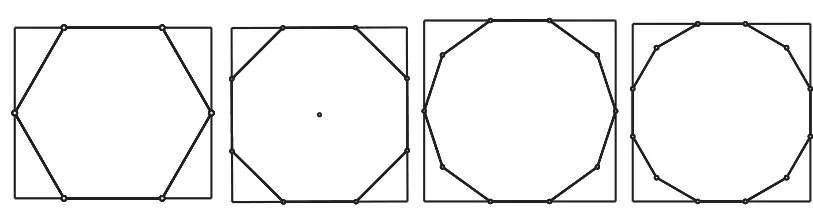
图5　正多边形及其外接矩形

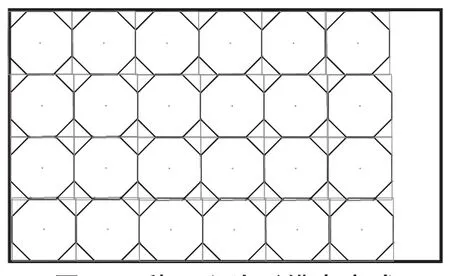
图6　一种正六边形排布方式

所以，对于烤箱空间利用率和烤盘均匀受热程度这两大因素的考量（在模型中具体表现为p和1-p），以及不同的烤箱的性质（在模型中具体表现为W/L），都可以通过评价函数求出与不同烤盘相应的fi.当烤盘i对应的fi最大时，则表示在综合考虑两个因素下，烤盘i是满足条件的最佳烤盘.

4　模型测试

随机选取美的型号为ETC56MY-ERS的烤箱进行仿真测试，其长595 mm，宽575 mm，平均每个烤盘面积为7 853.98 mm2，一共有3种形状烤盘可选：矩形烤盘（长宽比为1/2）、正方形烤盘和圆形烤盘.

根据模型2，计算出对应烤盘的最大数目N1，N2，N3.而由模型1，即二维热传导模型，可以计算出在相同时刻，3种烤盘温度的方差H1，H2，H3.最后再结合评价函数模型中的权重分配系数p和（1-p），得到结果如表4所示：

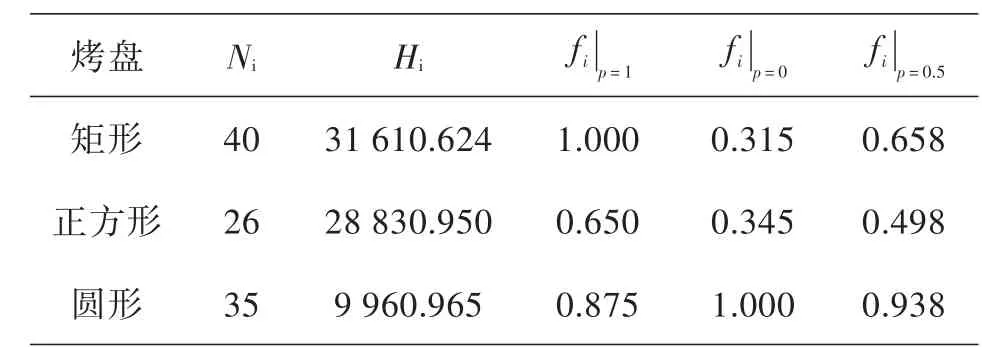
表4　仿真测试结果

5　模型评价

5.1优点

（1）基于热量与温度之间的线性关系，本文建立了二维的热传导模型，通过这个模型发现每个烤盘的温度分布情况，间接反映了烤盘的热量分布情况.除此以外，利用热传导模型，可以得到受热烤盘的瞬时热量分布情况，呈现烤盘受热的整个动态过程.

（2）利用数学软件MATLAB，我们可以直接求出以三维图像呈现的结果.而在图像中，通过不同的颜色，我们在图中分析受热烤盘的温度分布情况，其中蓝色表示低温，红色表示高温.另外，该软件的PDE工具箱可以帮助我们快速地求解热传导模型中的偏微分方程，而且其以图像这种直接的形式呈现结果，为后续的分析节省了时间，提高了解决问题的效率.

（3）本文给出的是针对某种烤箱最佳烤盘的挑选方法，若是实际中的烤箱数据不同，我们可以根据实际情况，修改热传导模型中的边界条件方程，同样也可以求解出符合要求的最佳烤盘.

5.2缺点

（1）本文只就几种特殊的烤盘形状进行分析，忽略了其他形状的烤盘，这样可能会使优化结果局限在有限的烤盘形状之内.

（2）本文假设烤盘的上下两个表面在加热过程中都是均匀受热的，仅考虑其余的侧面的受热情况，这可能与实际结果存在细小误差.

参考文献：

［1］LUIKOV A V. Analytical Heat Diffusion Theory［M］. New York：Academic Press, 1968：219-513.

［2］CARSLAW H S, JAEGER J C. Conduction of Heat in Solid［M］. Oxford：Oxford University Press, 1986：147-326.

［3］BERTOLA V, CAFARO E. Incorporating boundary conditions in the heat conduction model［J］. International Journal of Heat and Mass Transfer, 2009, 52（3/4）：644-646.

［4］刘连寿，王正清.数学物理方法［M］.北京：高等教育出版社，1990：86-268.

［5］熊静，张薇. MATLAB PDE-tool在热传导问题中的应用［J］.工业加热，2009，38（4）：42-44.

An Optimization Analysis of Pan Shape Based on Temperature Distribution

HUANG Jiaxin
（School of Mathematical Science, South China Normal University, Guangzhou 501631, China）

Abstract：Based on the analysis of the space utilization of an oven and the temperature distribution of the heated pans affecting different pan shapes, this paper finds the reason why the product at the edges has been overcooked when using a rectangle pan. Moreover, according to the fact and requirement of the problem, the author proposes the optimization model for designing the ultimate baking pan. The model simulation and evaluation are performed. During the model simulation, the results are also proposed when the p changes. In the model evaluation, strengths and weaknesses are analyzed for different models.

Key words：temperature distribution；heat conduction equation；evaluation function；parameter quantification

中图分类号：O242.2

文献标识码：A

文章编号：1008-2794（2016）02-0100-05

收稿日期：2015-02-15

通信作者：黄嘉欣，硕士研究生，研究方向：数学建模，E-mail：garfieldhjx@hotmail.com.