求解绝对值方程的PRP型梯度算法

祝文娟，严　涛

（南京理工大学理学院，江苏南京210094）

求解绝对值方程的PRP型梯度算法

祝文娟，严涛

（南京理工大学理学院，江苏南京210094）

摘要：给出了一种求解绝对值方程Ax -|x | = b的新方法.在矩阵A为对称正定的假设条件下，绝对值方程可转化为一个无约束优化问题，进而用PRP共轭梯度型方法对转化的无约束优化问题进行求解，从而获得原问题的解.证明了新算法在适当条件下可收敛到原问题的解.数值实验也表明了新方法的有效性.

关键词：绝对值方程；PRP共轭梯度法；收敛性；无约束最优化

1　相关基础知识

绝对值方程（Absolute Value Equation，简记为AVE）定义如下：

其中对称正定矩阵A∈Rn×n,b∈Rn，|x|表示对x的各个分量取绝对值.它是一类不可微的NP-hard优化问题.从形式上，问题（1）是绝对值方程Ax + B|x | = b的重要子类［1］.

绝对值方程的研究来源于两个方面，一个是区间线性方程［2］，另一个是线性互补问题.在理论方面，目前对于问题（1）的研究主要集中在解的存在性条件、唯一性条件、替代定理以及各种等价转化形式［2-3］.算法研究主要是以各等价问题为基础构造算法进而求解原问题，并进行相应的收敛性分析.现有算法可以归结为以下几类，一是利用绝对值方程与线性互补问题的等价性，将绝对值方程转化为线性互补问题，然后通过求解转化后的线性互补问题求得原问题的解［4］.二是将绝对值方程光滑化，等价转化成求解一个非线性方程组［5-6］.三是利用迭代算法来求解绝对值方程，即将绝对值方程转化为一个可微函数f（x），则问题（1）求解等价于求解无约束优化问题［7-9］.文献［9］中利用Armijo步长搜索规则，运用最速下降法来求解转化的无约束优化问题.但最速下降法产生的迭代点列移向极小点的路径呈“锯齿状”.随迭代点越来越接近极小点，目标函数下降得越来越缓慢，因而迭代点列收敛速度较慢.

定义1.3设f：D⊂Rn→R1,D是非空凸集，如果存在一个常数β＞0,对任意的x,y∈D和任意的α∈（0,1）有αf（x）+（1 -α）f（y）- f（αx +（1 -α）y）≥（1 -α）αβ‖x- y‖2,则称f（x）在凸集D上是一致凸函数.

定理1.1［3］若矩阵A的奇异值大于1，则对任意的b∈Rn，绝对值方程存在唯一解.

引理1.1若矩阵A为对称正定的，则存在向量P≠0及实数s＞0使得PTAP≥s‖P‖2.

证明设n维矩阵A的特征值为λ1,...,λn,令s= min（λ1,...,λn）,则s＞0.故A - sE的特征值为λ1- s,λ2- s,...,λn- s均非负.又因为A - sE均为实对称矩阵，则PT（A - sE）P≥0,P≠0,则PTAP≥sPTP.即PTAP≥s‖P‖2.

2　算法及收敛性分析

对于问题（1）中的对称矩阵A∈Rn×n,b∈Rn可构造如下模型［8］：

由于f（x）是连续可微的，则有∇f（x）= 2（Ax -|x | - b）,∇2f（x）= 2（A - D）= 2C ,其中D = diag（sign（x）,xi∈［- 1,1］, i= 1,2,...,n .

定理2.1［8］当矩阵C = A - D是正定时，x∈Rn是（1）的解当且仅当x为f（x）的最小值点.

定理2.2［5］若矩阵A的奇异值大于1，则区间矩阵［］A - I,A + I是正则的，故矩阵C为非奇异矩阵.

由上可知，绝对值方程（1）的求解可以转化为以下无约束优化问题：

则，进一步有：

引理2.1［9］x是绝对值方程（1）的解当且仅当∇f（x）= 0 .

以上述理论为基础，为了适应大规模绝对值方程求解问题，我们将给出求解无约束优化问题（3）的PRP型梯度算法，为区别于文献［9］及方便收敛性分析.本文的算法采取精确线性搜索，具体描述如下：

算法2.1

步骤1初始化：选取初始点x1，参数ε∈（0,1），计算g1=∇f（x1），令d1= -g1,k：= 0；

步骤2如果‖gk‖≤ε,则停；否则，利用精确线性搜索求αk，即f（xk+αkdk）= mα＞in0f（xk+αdk）, xk + 1= xk+αkdk.

步骤3计算∇f（xk + 1）,令gk + 1=∇f（xk + 1）.

步骤4利用下列公式来计算参数βk：

步骤5令dk + 1= -gk + 1+βkPRPdk,k：= k + 1.返回步骤2.

下面我们给出算法2.1的收敛性分析，首先给两个引理.

引理2.2［10］设∇f（x）在水平集L（x（0））=｛x|f（x）≤f（x（0））｝上存在且一致连续，下降算法的搜索方向d（k）与-∇f（x（k））之间的夹角θk满足θk≤π2-μˉ,μˉ＞0,∀k.步长αk由精确线性搜索确定.则或者对某个k,有∇f（x（k））= 0,或者有f（x（k））→-∞（k→∞）,或者有∇f（x（k））→0（k→∞）.

引理2.3矩阵C = A - D正定，则目标函数f（x）是Rn上的一致凸函数.

证明设u∈Rn,α∈R,考虑函数f（x +αu）在x处的二阶泰勒展开式，有

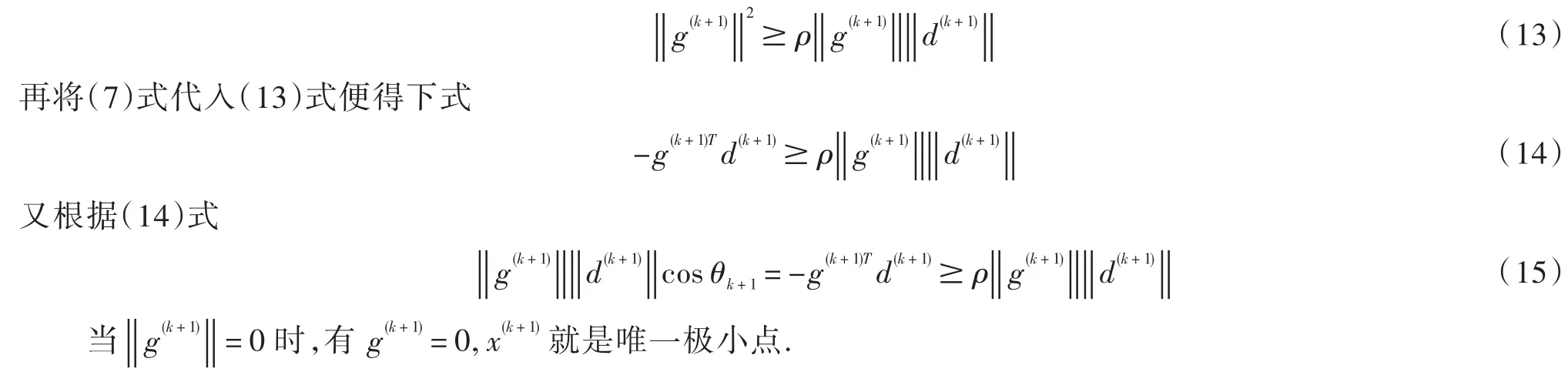
当‖g（k + 1）‖＞0时，由（15）式可得cos θk + 1≥ρ.由此可知存在μˉ＞0,使θk + 1≤-μˉ.由引理2.2知g（k + 1）→0,故g（x∗）= 0 .而由引理2.3知，x∗是唯一的极小点，所以x（k + 1）→x∗且x∗是极小点.

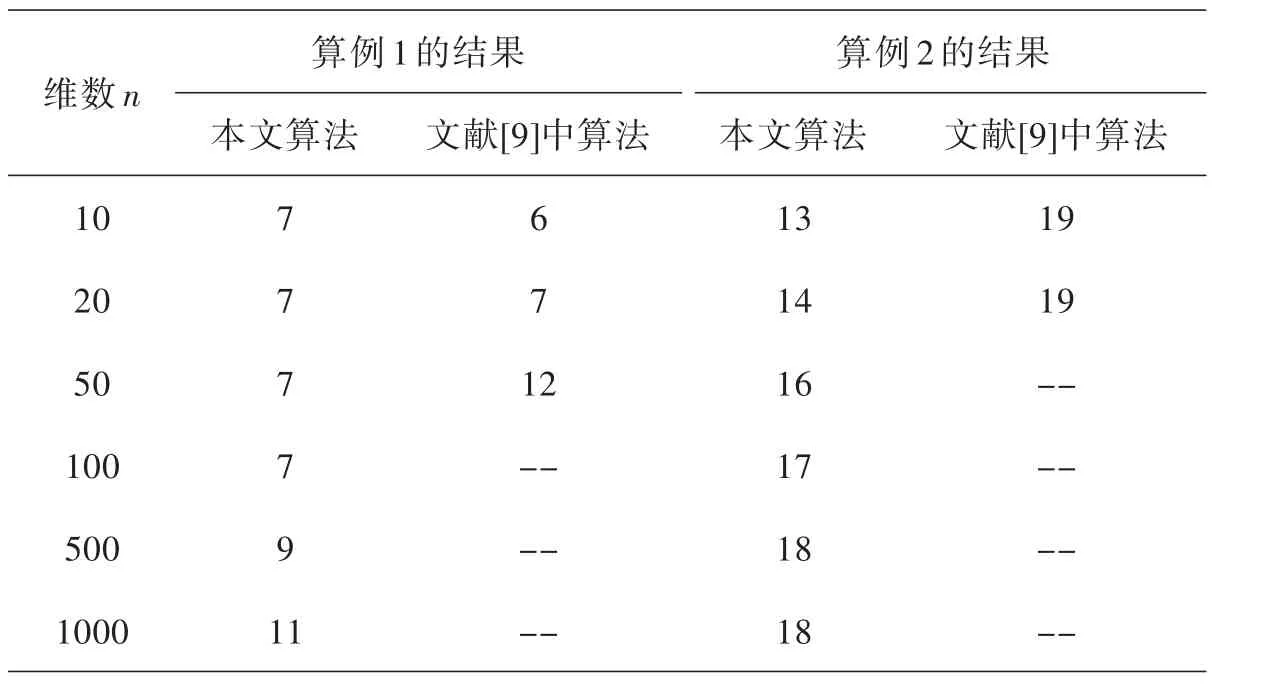
维数n算例1的结果本文算法　文献［9］中算法10 20 50 100 500 1000 777791 1 671 2 ------算例2的结果本文算法13 14 16 17 18 18文献［9］中算法19 19 --------

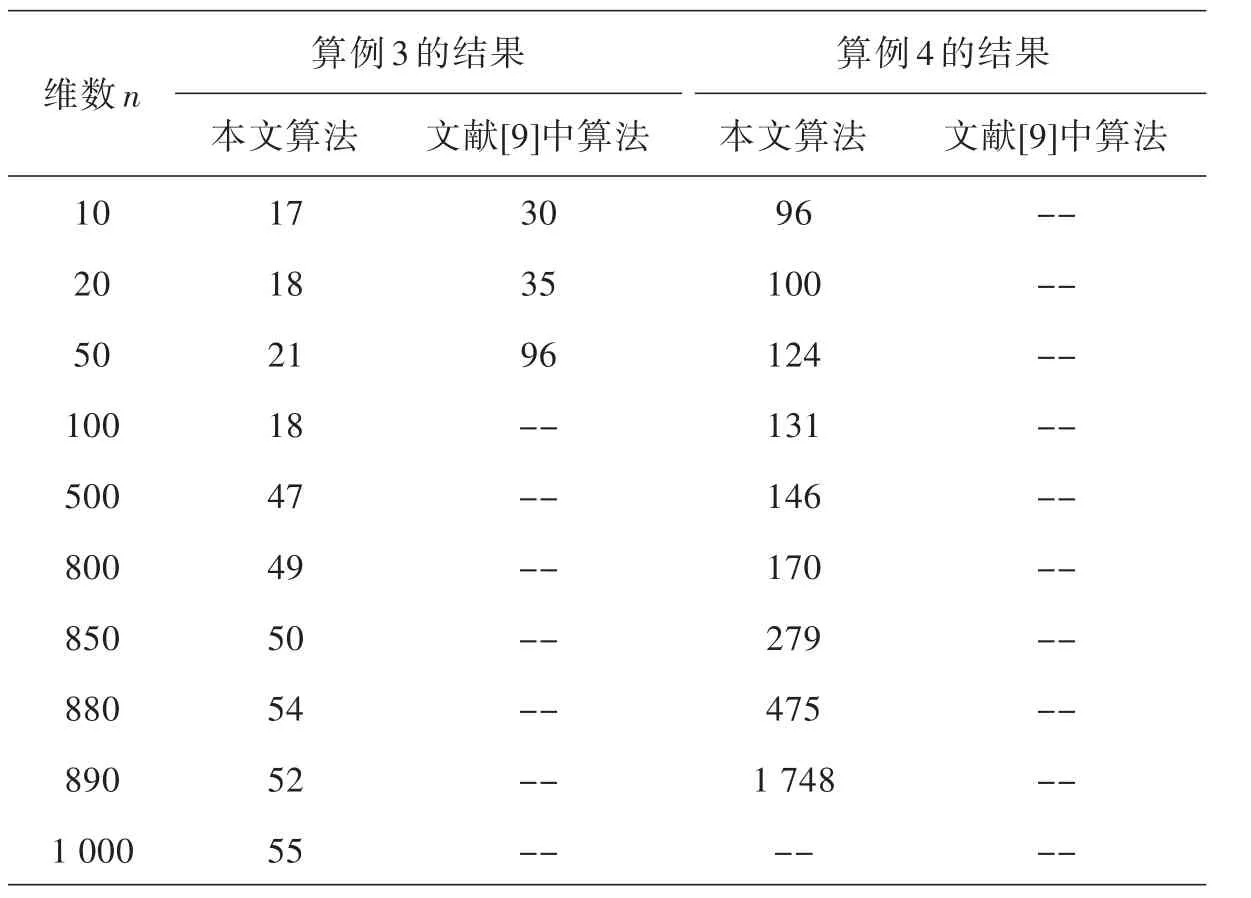
表2　算例3与算例4的实验结果

3　数值实验

在本节中，我们将给出数值实例来验证算法的有效性.我们选取文献［8］和文献［6］中的算例进行求解.停止准则为‖g（k）‖= 10-6，表中“--”表示在规定的最大迭代次数内没有得到问题的解.在本文中，我们设定最大迭代次数为2 000.算法程序用MATLAB R2 012b在4 GB RAM，CPU@1.70 GHz 2.40 GHz上运行.同时，为方便进行数值实验比较，我们将文献［9］中的算法完成程序后在同样的环境下运行.

算例1［8］矩阵A的元素定义为AT= A, aii= 500, aij= 1 + rand, i≠j,其中rand表示［0，1］中的随机数，令b =（A - I）e,其中I为n维单位矩阵，e =（1,1,...,1）T,该问题存在唯一解x =（1,1,...,1）T.

算例2［8］矩阵A的元素定义为aii= 4n,ai,i+ 1= ai+ 1,i= n,aij= 0.5,i,j= 1,2,...,n. 令b =（A - I）e,其中I为n维单位矩阵，e =（1,1,...,1）T,该问题存在唯一解x =（1,1,...,1）T.

我们设定算例1的初始点为x0=（0,0,...,0）T，算例2的初始点为x0=（x1,x2,...,xn）T,xi= 0.001∗i .在规定的最大迭代次数内，我们的算法能有限中止，获得问题的唯一解.而文献［9］中的算法只有在维数较小时才能在规定的最大迭代次数内获得问题的唯一解.我们在表1给出了算例1和2的具体迭代步数.

算例3和算例4中的矩阵A由文献［6］中的MATLAB程序生成.问题具有唯一解x =（1,1,...,1）T.我们设定算例3和4的初始点为x0=（10,10,...,10）T.我们的算法能在有限步数内获得问题的唯一解.而文献［9］中的算法对于算例3只有在维数较小时才能在有限步数内获得问题的唯一解，但对于算例4在规定的最大迭代次数内不能得到问题的解.我们在表2给出了算例3和4的具体迭代步数.

从上述数值结果可以看出，本文的算法具有一定的有效性，与文献［9］中给出的下降算法相比，本文的算法在求解维数较大的问题上有一定优势，除算例4（n=1 000）外，其他测试问题均能在满足停机准则下有限中止，得到问题的唯一解，且迭代次数较少.

4　结束语

本文先直接将绝对值方程等价转化为一个可微的无约束优化问题，然后采用共轭梯度法对该无约束优化问题进行迭代求解从而获得原问题的解.理论证明和数值实验表明，本文的算法是可行的，并且适合求解维数比较高的绝对值方程.因此本文的算法可作为求解绝对值方程问题的一个有效算法.

参考文献：

［1］ROHN J. Systems of Linear Interval Equations［J］. Linear Algebra and Its Applications, 1989（126）：39-78.

［2］ROHN J. A Theorem of the Alternatives for the Equation Ax + B|x| = b［J］. Linear And Multilinear Algebra, 2004, 52（6）：421-426.

［3］MANGASARIAN O L, MEYER R R. Absolute value equations［J］. Linear Algebra and Multiplication, 2006, 419（5）：359-367.

［4］PROKOPYEV O. On equivalent reformulations for absolute value equations［J］. Computational Optimization and Applications, 2009, 44（3）：363-372.

［5］ZHANG C, WEI Q J. Global and Finite Convergence of a Generalized Newton Method for Absolute Value Equations［J］. Journal of Optimization Theory and Applications, 2009, 143（2）：391-403.

［6］雍龙泉，拓守恒.基于凝聚函数的拟牛顿算法求解绝对值方程［J］.系统科学与数学，2012，32（11）：1427-1436.

［7］NOOR M A, IQBAL J, KHATTRI S, et al. A new iterative method for Solving absolute value Equations［J］. International Journal of the Physical Science, 2011, 6（7）：1793-1797.

［8］NOOR M A, IQBAL J, NOOR K I , et al. On an iterative method for solving absolute value Equations［J］. Optimization Letters, 2012, 16（5）：1027-1033. DOI：10.1007/s11590-011-0332-0.

［9］王炳囡.绝对值方程的算法及其收敛性分析［D］.曲阜：曲阜师范大学，2012：32-36.

［10］徐成贤，陈志平，李乃成.近代优化方法［M］.北京：科学出版社，2002：98-98.

The PRP Conjugate Gradient Algorithm for Solving the Absolute Value Equations

ZHU Wenjuan, YAN Tao
（School of Science, Nanjing University of Science and Technology, Nanjing 210094, China）

Abstract：In this paper, the authors propose a new algorithm for solving the absolute value equation（AVE）：Ax -| | x = b. Under the condition of coefficient matric A , which is symmetric and positive definite, absolute value equation is equivalent to an unconstrained optimization problem. The authors apply the PRP conjugate gradient algorithm for solving the absolute value equation based on the unconstrained optimization problem. The convergence of the proposed method is discussed under suitable conditions. Besides, numerical results are presented to show the efficiency of the new method.

Key words：absolute value equations；PRP conjugate gradient method；convergence；unconstrained optimization

中图分类号：O24

文献标识码：A

文章编号：1008-2794（2016）02-0086-05

收稿日期：2015-12-01

基金项目：国家自然科学基金“对称锥均衡约束规划的算法研究”（11101214）

通信作者：严涛，副教授，博士，研究方向：最优化方法，E-mail：tyan@njust.edu.cn.