《离散型随机变量及其分布列》教学再认识

冯 法

（新疆维吾尔自治区乌鲁木齐市外国语学校第十二中学，新疆乌鲁木齐 830006）

一、离散型随机变量的分布列的概念

概念的内涵指的是概念所反映对象的本质特征。

数学概念的教学应从创设概念生长点的问题情境切入探究。“问题是数学的心脏”，数学活动是由“情景问题”驱动的，“问题解决”是其主要的活动形式，创设可以连续变式的正多面体的问题情境，提出从低纬度向高纬度发展的问题是历经数学概念再创造的好的开始。层层递进的过程中，逐步丰富和建构对概念中位数本质意义的理解，即将“促进学生理解”始终贯串在整个课堂中。

引入随机变量的概念，是把对随机现象统计规律的研究数学化，从而可以利用数学方法研究随机现象的规律性。其中对随机变量的概率分布的研究是实现这种转化的关键。

本节的内容“分布列”是一种列举方式，是将试验结果整理的过程。在这个表格中，我们可以直观的找到某一事件所对应的片段，进而对整个试验有较为完整的认识。

例如：一袋中装有5只球，编号为1，2，3，4，5，在袋中同时取3只，以ξ表示取出的三只球中的最小号码，写出随机变量ξ的分布列.

首先，明确试验结果的可能性，然后再给予随机变量的取值。其中第一行中每个数字的含义给出更为具体的解释，如：“4”表示最小号码为4。在此基础上，根据随机变量相应的取值，求对应的概率。

对应练习：

判断下列表格是否可以作为分布列：

?

?

?

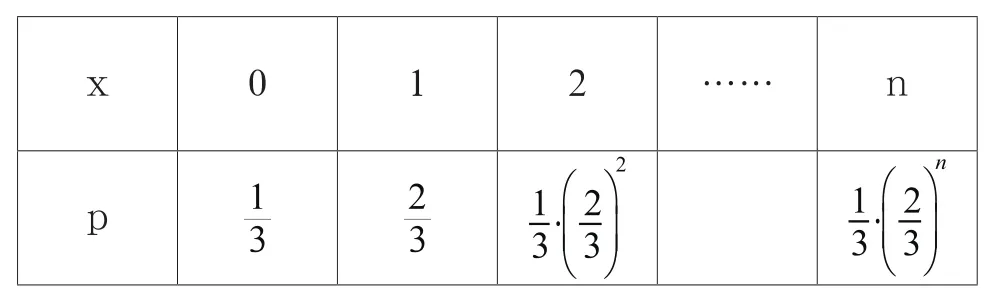
二、对分布列的应用探究

概念的外延指的是概念所反映的本质属性的对象，概念的内涵是质的方面，概念的外延是概念量的方面，它说明概念所反映的事物有哪些。

离散型随机变量的分布列的性质是概念的外延，而离散型随机变量的概率分布列的内涵是一个必然事件分解成有限个互斥事件的概率的另一种表示形式，更主要的是应在概念的生成中形成解决问题的思维方法。

借助于“引导式”教学、采用“剥洋葱皮”的方式从概念的外延出发探寻其内涵。循序渐进，逐层推进。基于此，设置问题，引发学生的思考。

问题1：通过简单的离散型随机变量的分布列，学生交流归纳并验证分布列具有哪些性质。

其中，性质2的理解是本节课的一个难点，结合实例，设置如下问题串：

道路因素实际上是目前车载导航主要考虑的方面。车载导航通过内置的地图匹配，即map matching功能，将实时定位的电动汽车位置与实际道路相匹配，便可获取车辆当前行驶道路的信息，从而完成实时路径规划[9]。事实上，在对电动汽车出行路径进行规划时，道路实时条件是出行时间的一大组成部分。

例：若某随机变量ξ的分布列如表所示

3456

问题2：性质2的含义是什么？

问题3：每一个分布列有多少个随机事件？

问题4：随机事件之间是什么关系？

问题5：这些随机事件构成的复杂事件又表示什么事件？

问题6：在掷一枚硬币的随机试验中，令如果正面向上的概率为P，随机变量X的分布列应该怎么表示？

对应练习：

1.随机变量ξ的分布列为

（1）求常数a；

（2）求P(1＜ξ＜4)

2.抛掷两枚骰子，点数之和为X，请列出变量分布表，并求点数之和为3的倍数的概率。

3.某城市有甲、乙、丙3个旅游景点，一位客人游览这3个景点的概率分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响.设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.

(1)求ξ的分布列及数学期望；

(2)记“函数 在区间(2，＋∞)上单调递增”为事件A，求事件A的概率.

三、教学上要做整体的把握，应该从基本点出发，形成交汇点，进而达到制高点

教学的基本点就是“双基”：数学基础知识和基本技能。从双基出发，使得基础知识形成网络、基本技能形成规律。制高点是重点，是可以达到必要深度的部分，但又不仅仅是重点。重点只是数学的结果，不指向如何应对；而制高点致力于探寻问题解决的基本思路，形成解决问题的方法和规律。站在制高点上进行教学设计，就是首先要准备贯彻什么样的教学理念、采用什么样的教学方法为支撑下的教学设计。所以在教学时应重视情境预设、更重视思维的发展历程，关注知识的内化、更关注形成知识的方法的理性建构，努力对课堂教学不断地进行积极的、有意义的开发与探索。

[参考文献]

[1] 中华人民共和国教育部.普通高中数学课程标准[S].北京：人民教育出版社，2003.

[2] 廖金祥，朱晴晴.“直线的一般式方程”的教学分析及教学思考[J].中学数学教学参考，2015，19：29-31+34.

[3] 方厚良，罗灿.泰勒的思维“六步骤”范式及其应用[J].中学数学教学参考，2015，28：29-31.

[4] 田载今.“离散型随机变量”的教学设计之我见[J].中小学数学(高中版)，2010，04：37-39.