一类四维超混沌系统全局指数吸引集的新结果

尹社会，张　勇

(河南工业职业技术学院基础教学部，河南 南阳 473000)

一类四维超混沌系统全局指数吸引集的新结果

尹社会，张勇

(河南工业职业技术学院基础教学部，河南 南阳 473000)

[摘要]基于微分方程的基本理论和方法，采用理论分析和计算机模拟相结合的方式，利用微分方程比较定理研究了一类四维超混沌系统的全局指数吸引集.对于系统的不同参数，得到了该超混沌系统全局吸引集统一的数学表达式，同时得到了正半轨线的速率估计.最后，用计算机模拟验证了计算理论的正确性.该研究结果为超混沌系统的混沌控制、混沌同步、吸引子维数的估计提供了理论依据.

[关键词]超混沌系统；全局指数吸引集；混沌同步；计算机仿真

0引言

混沌理论可以追溯到1900年庞加莱关于三体问题的研究.混沌系统的发展大致可以分为4个阶段[1]：第1阶段从1900年至1974年，主要贡献为三体问题、KAM理论、蝴蝶效应Lorenz混沌吸引子的发现、Henon映射的研究；第2阶段从1975年至1989年，主要贡献为Logistic人口模型的提出、混沌同步理论的提出、Chua电路的发现；第3阶段从1990年至1999年，主要贡献为混沌控制OGY方法的实现、混沌系统同步的实现、混沌保密通信的研究、混沌反控制的提出、Chen系统的提出；第4阶段从2000年至今，随着复杂网络的进一步研究与发展，从而推动了混沌理论的发展，主要贡献为复杂网络同步的研究.

混沌系统有着对系统初值和系统参数的敏感依赖性.1963年，美国气象学家Lorenz在研究大气层的热对流问题时发现了第1个混沌模型即Lorenz混沌系统；1999年，陈关荣等[2]提出了一类与Lorenz系统为对偶系统的Chen混沌系统；2002年，Lü等人[3]提出了一类处于Lorenz与Chen之间的过渡系统，即Lü混沌系统，同年Lü等人[4]提出了统一混沌系统模型；2007年，王兴元[5]等提出了超混沌Lorenz系统.人们不断发现新的混沌系统，并且揭示新的动力学特性是动力系统的一个重要研究方向.混沌系统在数学、物理、化学、电路、混沌保密通信、图像加密、控制理论、激光、神经网络等领域都有着非常重要的应用价值[6-24].本文研究了一类新超混沌系统的动力学行为，该结果将为超混沌系统的混沌控制、混沌同步、吸引子维数的估计提供理论依据.

1动力系统模型及其主要结果

一类新超混沌系统的动力系统模型为[25]：

(1)

其中A，b，c，d，e，f，g，h均为系统(1)的正参数.并且当A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1 时，系统(1)存在一个典型的超混沌吸引子[25].

当A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1时，系统(1)轨线相图见图1.

图1　系统(1)轨线的相图

定理对于任意的A>0，b>0，c>0，d>0，e>0，f>0，g>0，h>0，令：

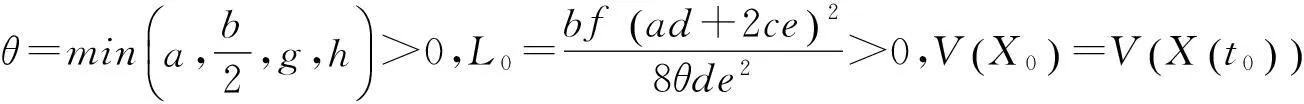
(2)

取上极限得

从而

为系统(1)的一个全局指数吸引集.

证明定义

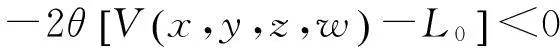
从而有

(3)

令t→+∞，取上极限得

从而

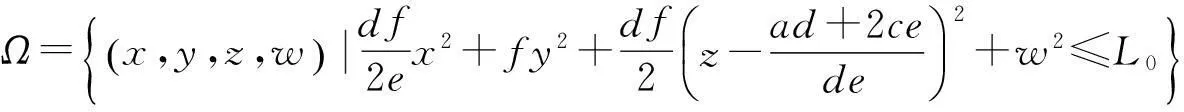
为系统(1)的一个全局指数吸引集.其中

说明：

图2　系统(1)的正半轨线最终进入椭球之内

(1)本文得到系统(1)的最终界估计不仅比文献[25]中的界估计结果更准确，而且给出了轨线的速率估计.

(2)取参数A=35，b=4，c=25，d=5，e=35，f=100，g=1，h=1，由定理可知系统(1)的一个全局指数吸引集为

系统(1)的正半轨线在xyw相空间中的最终界估计见图2.

2结论

本文基于微分方程的理论与方法研究了一类超混沌系统的全局指数吸引集，得到了其统一的数学表达式.该研究结果为系统电子振荡电路的实现和通信工程设计等应用提供了理论依据.

[参考文献]

[1]闫振亚.复杂非线性波的构造性理论及其应用[M].北京：科学出版社，2002：15-17.

[2]CHEN G R，UETA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos，1999，9(7)：1465-1466.

[3]LÜ J H，CHEN G R.A new chaotic attractor coined[J].International Journal of Bifurcation and chaos，2002，12(3)：659-661.

[4]LÜ J，CHEN G，CHENG D，et al.Bridge the gap between the Lorenz system and the Chen system[J].International Journal of Bifurcation and Chaos，2002，12(12)：2917-2926.

[5]WANG XINGYUAN，WANG MINGJUN.A hyperchaos generated from Lorenz system[J].Physica A：Statistical Mechanics and Its Applications，2008，387(14)：3751-3758.

[6]汪威，朱晓刚，李俊杰，等.Feigenbaum 吸引子的动力性质[J].东北师大学报(自然科学版)，2014，46(4)：48-51.

[7]梁春辉，张运波，孟祥萍，等.自适应反演控制在一类非线性系统中的应用[J].东北师大学报(自然科学版)，2014，46 (4)：66-71.

[8]汪威，李健，朱晓刚，等.一类代换系统及其超空间系统[J].东北师大学报(自然科学版)，2015，47(3)：9-11.

[9]SONG ZIGEN，ZHEN BIN，XU JIAN.Species coexistence and chaotic behavior induced by multiple delays in a food chain system[J].Ecological Complexity，2014，19：9-17.

[10]SONG ZIGEN，XU JIAN，LI QUNHONG.Local and global bifurcations in an SIRS epidemic model[J].Applied Mathematics and Computation，2009，214：534-547.

[11]SONG ZIGEN，XU JIAN.Stability switches and double Hopf bifurcation in a two-neural network system with multiple delays[J].Cognitive Neurodynamics，2013，7：505-521.

[12]SONG ZIGEN，XU JIAN.Stability switches and multi-stability coexistence in a delay-coupled neural oscillators system[J].Journal of Theoretical Biology，2012，313：98-114.

[13]WANG XINGYUAN，HE GUOXIANG.Cryptanalysis on a novel image encryption method based on total shuffling scheme[J].Optics Communications，2011，284(24)：5804-5807.

[14]赵国辉，舒永录.一个新超混沌系统的控制与自适应同步[J].重庆工商大学学报(自然科学版)，2011，28(1)：1-7.

[15]何兴，舒永录，赵显锋.离散混沌系统的脉冲控制[J].重庆工商大学学报(自然科学版)， 2010，27(5)：431-434.

[16]张勇，付木亮.高维混沌模型的动力学分析及仿真[J].江西科学，2015，33(2)：160-161.

[17]袁红，张付臣，李小武.关于 Hopf 分岔中向量函数泰勒公式中算子系数表示的评注[J].重庆工商大学学报(自然科学版)，2012，29(10)：6-10.

[18]汤志浩，张勇.几类高维类 Lorenz 混沌模型的稳定性分析及其仿真[J].江西科学，2015，33(4)：464-466.

[19]HE XING，YU JUNZHI，HUANG TINGWEN，et al.Neural networks for solving nash equilibrium problem in application of multiuser power control[J].Neural Networks，2014，57(9):73-78.

[20]HE XING，LI CHUANDONG，HUANG TINGWEN，et al.A recurrent neural network for solving bilevel linear programming problem[J].IEEE Transactions on Neural Networks and Learning Systems，2014，25(4)：824-830.

[21]LIU HONGJUN，WANG XINGYUAN.Color image encryption using spatial bit-level permutation and high-dimension chaotic system[J].Optics Communications，2011，284(16)：3895-3903.

[22]LEONOV G，KUZNETSOV N.Hidden attractors in dynamical systems.From hidden oscillations in Hilbert-Kolmogorov，Aizerman，and Kalman problems to hidden chaotic attractor in Chua circuits[J].International Journal of Bifurcation and Chaos，2013，23：1330002-1-1330002-69.

[23]ZHANG FUCHEN，SHU YONGLU，YANG HONGLIANG.Bounds for a new chaotic system and its application in chaos synchronization[J].Communications in Nonlinear Science and Numerical Simulation，2011，16(3)：1501-1508.

[24]ZHANG FUCHEN，SHU YONGLU，YANG HONGLIANG，et al.Estimating the ultimate bound and positively invariant set for a synchronous motor and its application in chaos synchronization[J].Chaos，Solitons & Fractals，2011，44(1)：137-144.

[25]张晓丹，崔丽娟.一类四维超混沌系统的界及同步的研究[J].物理学报，2011，60 (11)：1-7.

(责任编辑：石绍庆)

New results of globally exponentially attractive set for a class of hyperchaotic systems

YIN She-hui，ZHANG Yong

(Department of Basic Teaching，Henan Polytechnic Institute，Nanyang 473000，China)

Abstract:Based on the theory and the method of differential equations，this paper investigates complex dynamical behaviors of a new class of hyper-chaotic systems by theoretical analysis and matlab simulation combined method.The global attractive sets of this hyperchaotic system are obtained.In this paper，the unified mathematical expression of the global attractive sets of the system are obtained by the comparison theorem of differential equations.Finally，computer simulation verifies the correctness of the theoretical calculation.This article provides a theoretical basis for chaos control，chaos synchronization，the attractor dimension estimate of this system.This method can be extended to study other chaotic systems.

Keywords:hyperchaotic system；globally exponentially attractive set；chaos synchronization；computer simulation

[文章编号]1000-1832(2016)02-0052-04

[收稿日期]2013-12-14

[基金项目]河南省基础与前沿技术项目(142300410416)；南阳市科学技术发展规划项目(2012GG035).

[作者简介]尹社会(1979—)，男，硕士，讲师，主要从事物理、混沌控制等研究；通讯作者：张勇(1981—)，男，硕士，讲师，主要从事数学理论研究.

[中图分类号]O 241.84；O 29；O 242.1[学科代码]110·61

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.013