基于双层规划的车辆路径问题研究

王一瓯，王海鹏，2

(1.宾夕法尼亚州立大学工程学院，宾夕法尼亚 16801；2.南开大学经济学院，天津 300071)

基于双层规划的车辆路径问题研究

王一瓯1，王海鹏1，2

(1.宾夕法尼亚州立大学工程学院，宾夕法尼亚 16801；2.南开大学经济学院，天津 300071)

[摘要]针对城市交通堵塞的问题，提出了一种基于车辆路径问题(VRP)和使用者均衡问题(UE)的双层优化模型.在其上层是车辆路径选择问题的一种拓展，在其下层采用用户均衡交通分配模型对城市交通中的货运车辆和客运/通勤车辆进行第一原理性的数学刻画.结果表明：VRP-UE模型不但可以提出能够规避堵塞的交通方案，而且可以减少车辆本身可能带来的交通阻塞；采用双层优化模型可以显著降低车辆出行的时间成本.

[关键词]车辆路径；双层规划；城市物流

0引言

自1959年Dantzig和Ramser提出车辆路径选择问题以来[1]，该问题已成为最著名的组合优化问题之一.学术界在此领域取得了一系列的成果[2]，文献中提出了几个经典车辆路径选择问题的扩展，如随机车辆路径(SVRP)[3]、鲁棒车辆路径(RVRP)[4]以及带时间窗口的车辆路径选择问题(VRP-TW)[5].

交通堵塞已经成为影响城市发展和人民生活的重要问题之一.学术界对存在交通堵塞情况下的车辆出行问题的研究也已取得一些成果，如文献[6]认为物流车辆经过不同节点时，所产生的时间成本不但与两节点间的距离有关，而且与此时的时间相关(TD-VRP)，因而交通拥堵可以由动态变化的时间成本来描述.而文献[7]采用的模型结构对本文最具启发性，该文献认为：在城市物流环境下，一方面就车辆路径选择问题的数学描述而言，物流车辆经过不同节点之间所产生的时间成本应由文献[8]中的仿真模型进行描述；另一方面，对城市交通状况进行模拟仿真的模型被认为物流车辆会按最短路径(shortest path)行驶于各个节点之间，但这仍然不是全局最优的车辆路径规划.

此外，学术界对于交通拥堵的第一原理描述已经发展得较为成熟，如用户平衡交通分配模型[9]和动态用户平衡交通分配模型[10]等.在城市交通环境下，多种车辆将参与交通，对这类行为的描述可以参见文献[11]中提出的多重平衡行为模型.

车辆路径选择(VRP)与拥堵情况下的用户动态均衡(UE)是2个交织在一起的相互动态影响的问题，单考虑一方面无法得到全局最优解.本文运用双层规划方法首次将两者进行结合，以(静态的)用户平衡交通分配模型描述城市物流中的交通拥堵现象，并得到基于全局最优解的车辆出行方案.

1问题描述

城市物流环境下交通道路网络上共有两类车辆：(1)用“通勤车辆”指代交通网络上已经存在的车辆，其指代各类小型客运车辆，本文采取用户平衡交通分配模型对这类车辆的行为进行描述；(2)用“物流车辆”指代需要本文模型进行规划的大型货运车辆.本文所提出的双层规划模型之所以将物流车辆置于问题的上层，是因为物流车辆是城市道路交通中有组织的、长期的、频繁的使用者，与一般通勤的交通参与者不同，这类使用者有能力利用此方面的优势对自身路径进行更好地规划.换言之，从Stackelberg博弈的意义上看，物流车辆应该在建模中处于博弈的领导层(Leader)，即上层.

在城市物流环境下双层车辆路径选择问题的几个特性.首先，在传统的车辆路径选择问题中，需要配送服务的客户由散落在二维平面中的点来描述，其位置和需求均已知.当设计配送路线时，这些节点可以任意被所设计的路线连接.而在城市物流环境下，客户位于描述城市交通网络的已知节点上，即必须在已有的网络上进行路径规划.其次，由于交通网络中存在上文所描述的两类车辆，而它们一类由整数变量描述，一类由连续变量描述，本文将引入类似于文献[11]对其进行描述.

整个双层规划车辆路径问题(VRP-UE)的数学模型是均衡约束规划问题，上层将是整数规划问题，其流程见图1.

图1　双层规划车辆路径选择模型的流程

2数学模型与分析

2.1符号说明

问题的决策变量有：

(1)

t0k=车辆k离开起始点的时刻，

(2)

tik=车辆k离开节点i的时刻.

(3)

2.2数学模型

根据上述变量和模型假设得到VRP-UE问题的数学模型.其上层问题的目标函数为

(4)

(1)上层问题的约束条件.每个客户只由某一辆配送车辆服务，即

(5)

每辆配送车辆的载货量约束为

(6)

配送车辆必须离开起始点为

(7)

配送车辆平衡为

(8)

每个客户仅能被一辆配送车辆服务一次，即

(9)

消除子回路为：

(10)

(2)连通双层车辆路径选择问题的一系列约束条件.假定所有配送车辆离开起始点的时间已知，即

t0k=Tk，∀k∈v;

(11)

实际上是变量ξ(i，j)的定义式表示将通过边(i，j)的配送车辆数量，于是有

(12)

上层中经过每条边的时间成本将由下层描述为

tik-tjk≥vijkC(i，j)(h*，ξ(i，j))，∀k∈v，i，j∈N.

(13)

下层的变分不等式(VariationalInequality)描述为求解h*∈Λ2使得

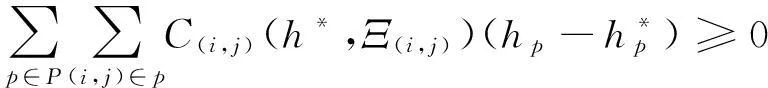
(14)

其中

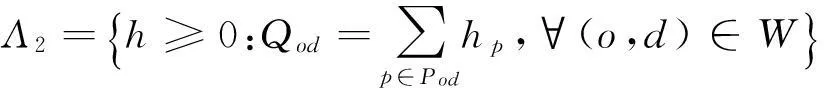
(15)

综上所述，本文所提出的双层车辆路径选择问题实际上是均衡约束规划问题的一个特例.其最优解的存在性：对于下层的变分不等式而言，上层的任意可行解只会改变交通网络相应边的车流量，从而使下层问题可解，又由于上层问题解空间的有限性，可知整体问题的最优解的存在.但是双层车辆路径选择问题最优解的唯一性及研究一般交通成本时算法的收敛性不能被保证.

2.3一个特例

本节考虑交通网络任意边运输成本为线性的情况时，则有

C(i，j)(f(i，j)，ξ(i，j))=α(i，j)f(i，j)+βf(i，j)ξ(i，j)+γ(i，j).

(16)

为了刻画物流车辆超大的体积等效应，引进系数β(i，j)以便将物流车辆转换成等体积的通勤车辆流进行考虑.则(14)—(15)可以转化为：

(17)

ρod≥0，∀(o，d)∈w；

(18)

(19)

ρod≤M(1-zod)，∀(o，d)∈w；

(20)

(21)

hp≥0，∀p；

(22)

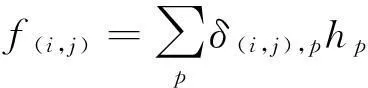
(23)

zod∈{0，1}，∀(o，d)∈w.

(24)

其中M是大的正整数.于是VRP-UE问题在这个特例中转化为混合整数线性规划问题，从而可以通过已有的程序包进行求解.在每边的通过时间成本对于车流量是多项式的形式时，类似的变形依然成立.

3实验与分析

3.1算例描述

Sioux Falls网络是交通科学领域应用最广泛的测试网络之一，该网络有24个节点、72条边.为了描述通勤车辆的交通分配，我们分别假设10对起点/终点与207条路径以及496对起点/终点和1 941条路径2种情况.本文中Sioux Falls网络的相关数据来自文献[12]，将模型转化至2.3中的混合整数规划问题之后，在MATLAB2012下调用了Gurobi 5.5程序包对问题进行了计算.

3.2结果与分析

将2种测试条件下得到的结果分别列于表1和2.在研究过程中分别设定了3个对照组：(1)对于不同客户节点，其货运需求是否相同；(2)对于不同物流车辆，其最大容量是否相同；(3)对于网络中通勤车辆，其总交通量是较大还是一般.为了验证双层车辆路径模型(VRP-UE)解的有效性，我们设计了对照计算实验方案：首先在忽略通勤车辆带来的交通堵塞的条件下，计算经典车辆路径模型(VRP)，将所得到的物流车辆路径选择问题与通勤车辆在一起进行使用者均衡交通分配，亦即在Ξ(i，j)已知的情况下求解(15)式，从而得到网络上每条边的通行时间成本，然后对所有物流车辆计算总的通行时间成本.在表1和2中，将以此方法得到的对照解称为“纳什-纳什”解.

表1　通勤车辆有10对起点/终点与207条路径

表2　通勤车辆有496对起点/终点与1 941条路径

从表1和2可知:在所考虑的交通网络中，对物流车辆的容量越细分，VRP-UE模型节约的时间成本越显著；对通勤车辆的描述越细致，VRP-UE模型节约的时间成本越显著.其中原因是由于VRP-UE 模型考虑了通勤车辆分配.这是本文提出的全局最优车辆通勤方案的优势所在.

另外，在图2和3中列出了由双层车辆路径选择模型(VRP-UE)和经典车辆路径选择模型(VRP)所给出的物流车辆的出行方案(参数设置对应表2中的第3个算例).发现VRP-UE模型给出了与经典VRP模型截然不同的物流车辆路径.

图2　经典路径选择模型解出的物流车辆路径

图3　双层规划车辆路径选择模型解出的物流车辆路径

综上所述，本文方法较不考虑交通拥堵的车辆路径优化方法而言，采用的双层优化模型(VRP-UE)可以显著降低货运的时间成本.

4结语

本文中的双层VRP-UE模型是第一个通过第一性原理同时刻画货运与客运/通勤辆在交通网络中行为的模型.一系列的计算实验表明，在以总货运时间成本最小为目标函数的情况下，考虑交通堵塞成本的双层模型所提出的货运方案，明显优于不考虑交通堵塞成本的VRP模型.在交通堵塞的情况下，VRP-UE模型不但可以提出能够规避堵塞的货运方案，而且可以减小货运车辆本身可能带来的交通阻塞.

[参考文献]

[1]TOTH P，DANIELE V.The vehicle routing problem[M].Philadelphia：Society for Industrial and Applied Mathematics，2001：1-26.

[2]DANTZIG G，RAMSER J.The truck dispatching problem[J].Management Science，1959，6：80-91.

[3]GENDREAU M，GILBERT L，RENE S.Stochastic vehicle routing[J].European Journal of Operational Research，1996，88：3-12.

[4]ORDONEZ F.Robust vehicle routing[M].Maryland：TUTORIALS in Operations Research，2014:153-178.

[5]GARCIA B，POTVIN J，ROUSSEAU J.A parallel implementation of the Tabu search heuristic for vehicle routing problems with time window constraints[J].Computers Operations Search，1994，21:1025-1033.

[6]MALANDRAKI C，MARK S D.Time dependent vehicle routing problems：formulations，properties and heuristic algorithms[J].Transportation Science，1992，26：185-200.

[7]TANIGUCHI E，ROB E.An evaluation methodology for city logistics[J].Transport Reviews，2000，20：65-90.

[8]FUJII S，IIDA Y，UCHIDA T.Dynamic traffic simulation to evaluate vehicle navigation systems[C]//In Vehicle Navigation and Information Systems Conference，Yokohama：IEEE Xplore，1994：239-244.

[9]FRIESZ T L.Transportation network equilibrium，design and aggregation：key developments and research opportunities[J].Transportation Research Part A：General，1985，19：413-427.

[10]FRIESZ T L，HAN K，NETO P A，et al.Dynamic user equilibrium based on a hydrodynamic model[J].Transportation Research Part B：Methodological，2013，47：102-126.

[11]YANG H，ZHANG X，QIANG M.Stackelberg games and multiple equilibrium behaviors on networks[J].Transportation Research Part B：Methodological，2007，41：841-861.

[12]Transportation Network Test Problems[EB/OL].2013-05[2015-12-07].http://www.bgu.ac.il/-bargera/tntp/.

(责任编辑：石绍庆)

A bi-level vehicle routing problem in urban logistics

WANG Yi-ou1，WANG Hai-peng1，2

(1.College of Engineering，Pennsylvania State University，PA 16801，USA；2.School of Economics，Nankai University，Tianjin 300071，China)

Abstract:Traffic congestion，caused by growing traffic volume on limited road networks，has become one of the most significant phenomenon of people’s daily life.In this paper a novel formulation of vehicle routing problem (VRP)as a bi-level optimization problem is proposed.The upper level problem is a generalization of VRP for the freight service provider.The lower level，which is a characterization of urban traffic congestion from first principle，takes on the form of user equilibrium (UE)traffic assignment of the commuters traffic.A series of numerical experiments on different networks shows a significant saving on total travel cost for the freight service provider compared to native applications of VRP.

Keywords:vehicle routing problem；bi-level optimization；urban logistics

[文章编号]1000-1832(2016)02-0093-06

[收稿日期]2015-12-07

[基金项目]国家自然科学基金资助项目(71372002).

[作者简介]王一瓯(1987—)，男，博士研究生，主要从事动态网络优化、博弈论研究.

[中图分类号]U 491.1[学科代码]580·70

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.020