球形机器人的建模与控制研究
2016-06-29王志群
王志群 刘 蕾 杨 彬 董 春
(北京交通大学电子信息工程学院1,北京 100044;北京交通大学电气工程学院2,北京 100044)
球形机器人的建模与控制研究
王志群1刘蕾2杨彬2董春2
(北京交通大学电子信息工程学院1,北京100044;北京交通大学电气工程学院2,北京100044)
摘要:设计了一种通过三个惯性轮驱动的球形机器人,基于角动量守恒定律实现机器人移动。利用四元数及Kane方程建模方法,建立了球形机器人的完整动力学模型,给出了控制其运动的微分方程组,进而设计一个自适应模糊滑模变结构控制器,以实现对参数及动力学模型不精确的球形机器人的位置控制。为了减弱系统的抖振,通过对滑模控制器中的切换项进行模糊逼近,使切换项连续化。轨迹跟踪的仿真和试验表明,该控制器在参数不确定和动力学模型不精确的系统中有良好的表现。
关键词:球形机器人动力学模型四元数Kane方程滑模变结构控制自适应模糊控制减振轨迹跟踪
VibrationreductionTrajectorytracking
0引言
球形机器人由球壳及内部驱动机构组成,它的运动原理主要为两种:一种是通过内部驱动机构改变系统的重心位置,如轮式质量块驱动[1]、位移质量块驱动[2]、两自由度摆驱动[3]等;另一种是改变系统的角动量,如双转子结构[4]、三自由度陀螺[5]等。
文献[6]提出的动力学模型,只适用于球形机器人的直线运动;而文献[7]摆杆驱动的球形机器人则采用反馈线性化的方法,设计直线轨迹跟踪的控制器。此外,直线轨迹跟踪控制器的设计方法还有:滑模变结构方法[8]、自适应分层滑模控制方法[9]、自适应神经模糊和滑模变结构控制相融合的方法[10]等。文献[11]对球形机器人的模型进行线性化,忽略内部驱动机构的动力学效应,设计了一个滑模变结构轨迹跟踪控制器;文献[12]则基于解耦的动力学模型并忽略机器人的横向及纵向旋转,设计了一个模糊控制器进行运动控制。
本文将研究使用惯性轮驱动的球形机器人,并设计滑模控制器实现平面轨迹跟踪。为了解决抖振的问题,采用模糊系统对滑模控制器的切换项进行逼近,从而实现控制信号的连续化。
1运动学与动力学建模
1.1运动学建模
受文献[13]、文献[14]的启发,本文设计了球形机器人结构。为便于建模及仿真,在此假设装配了3个惯性轮及相对应数目配重块的球形机器人的质心,刚好与球壳中心重合。设惯性坐标系为{1}(x1,y1,z1)。坐标系{2}(x2,y2,z2)与惯性坐标系{1}平行,原点与球心重合,坐标系{3}(x3,y3,z3)为球体坐标系,与坐标系{2}同原点,但是坐标系随着球的旋转而发生相应的旋转。对于坐标系{2}与坐标系{3}之间的旋转和平移关系,可用四元数表示如下:
(1)
(2)
由文献[15]可知,空间角速度与旋转四元数之间的关系可表示为:
(3)

由式(3)可计算得到球壳在坐标系{2}的角速度和角加速度:
(4)
式中:2ω1及2α1分别为球形机器人第1部分(即球壳)的角速度及角加速度向量在坐标系{2}中的描述。
球心的速度为:
2V1=2VI+2ω1×2rG/I=2ω1×Rsk2
(5)
式中:2V1为球形机器人第1部分(即球壳)质心位置的线速度向量在坐标系{2}中的描述;2VI为球形机器人与地面接触点间的速度向量;2rG/I为球形机器人几何中心到球壳与地面接触点间的位置向量在坐标系{2}中的描述;Rs为球壳半径。
(6)
(7)
由于配重块与球壳相连,因此它们的角速度及角加速度都与球壳相等,即:
(8)
式中:i=2,3,4。
3个惯性轮相对于坐标系{1}的角速度及角加速度分别为:
[3ω5,3ω6,3ω7]=[3ω1+Ωxi3,3ω1+
Ωyj3,3ω1+Ωzk3]
(9)
(10)

各惯性轮及配重块质心处的线速度及加速度为:
(11)

(12)
式中:i=1,2,3,4,5,6,7。
1.2动力学建模
球形机器人系统可由9个参数[q0,q1,q2,q3,x,y,θx,θy,θz]来描述,但是这些参数之间并不相互独立。以下由Kane法来推导机器人运动微分方程。
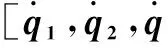
(13)

(14)
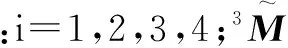
电机转子的惯性矩为:
(15)
电机产生的主动力矩可分别表示为:
(16)
式中:Tx、Ty、Tz为3个电机的输出转矩。
根据Kane法,计算出机器人各部位的线速度及角速度的偏导数为:
(17)
式中:i=1,2,3,4,5,6,7;j=1,2,3,4,5,6。
电机转子在坐标系{4}、{5}、{6}中相对角速度的偏导数分别为:
(18)
式中:j=1,2,3,4,5,6。
广义主动力和广义惯性力分别为:
(19)
式中:j=1,2,3,4,5,6;2Ri为球形机器人各部位所产生的主动力在坐标系{2}中的描述;3Mi为球形机器人各部位所产生的主动力矩在坐标系{3}中的描述。
(20)
式中:j=1,2,3,4,5,6。
式(19)和式(20)由Kane法表述为:
(21)
式中:j=1,2,3,4,5,6。
将式(21)化为如下球形机器人全状态运动学方程:

(22)
p=[q0,q1,q2,q3,x,y,θx,θy,θz]T
(23)
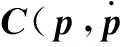
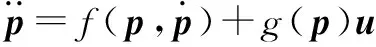
(24)
2控制系统设计
考虑建模误差、参数变化以及其他不确定因素,式(22)可以改写成以下形式:

(25)式中:ΔA、ΔC为建模误差及参数不确定;D为测量噪声及其他干扰。根据式(24)、式(25),可改写成以下形式:

(26)
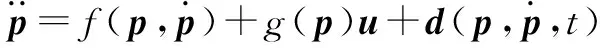
(27)
为了跟踪球形机器人系统的运动轨迹,系统输出矩阵设计为H=[x,y,θz]T,对输出矩阵取二阶微分,可得:
(28)
(29)
式中:H∈R3,H2∈R3×3,d∈R3,可由式(24)得到。
2.1滑模控制器设计
取球形机器人的位置及角度指令,分别为xd、yd、θzd,则轨迹的跟踪误差为:
e=[x-xd,y-yd,θz-θzd]T=[ex,ey,ez]T
定义切换函数为:
则:

(30)
式中:Hd=[xd,yd,θzd]T;K=[k1,k2,k3]T。
将滑模控制律设计为:
(31)
式中:usw=[ηxsgn(sx),ηxsgn(sy),ηθzsgn(sθz)]T,且ηx>E,ηy>E,ηθz>E。
由式(29)和式(30),可得:
(32)
将式(31)代入式(32),可得:
(33)

2.2自适应模糊滑模控制器设计
由于模糊系统具有万能逼近特性,利用自适应模糊控制方法,通过将滑模控制器中的切换项进行模糊逼近,可将切换项连续化,从而有效地降低抖振[16]。
分别为3个跟踪目标设计3个模糊系统,针对模糊系统输入分别设计3个模糊子集,各有3条模糊规则。采用乘积推理机、单值模糊器和中心平均解模糊器设计模糊系统[17],模糊系统的输出为F,引入模糊基向量Φ(s)=[φ1(s),φ2(s),φ3(s)]T,则式(31)所表示的控制律可变为:
(34)

理想的F(s|J)为F(s|J*)=ηsgn(s),其中η>E。
自适应律为:
J=γsφ(s)
(35)
式中:γ>0。
稳定性证明如下:

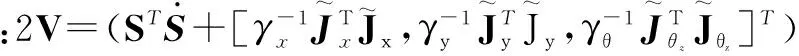

[ηx|sx|,ηy|sy|,ηθz|sθz|]T<0
3仿真及试验
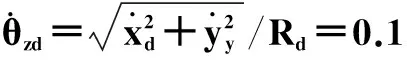

图1 为利用自适应模糊控制方法,将跟踪位置x滑模控制器中的切换项进行模糊逼近。将原先的切换项连续化,能够有效降低控制系统的抖振。
图2为圆周运动轨迹,2条轨迹表明球形机器人能够快速稳定地跟踪给定的轨迹。图3为跟踪误差曲线,采用曲线的形式,给出球形机器人进行圆周轨迹跟踪时,在x方向、y方向以及绕竖直转轴z方向的转角和跟踪误差。

图1 x方向的切换项及模糊逼近示意图

图2 圆周运动轨迹

图3 跟踪误差曲线
4结束语
本文研究了一种通过3个惯性轮驱动的球形机器人。在对机器人进行运动分析的基础上,利用四元数及Kane法,建立了球形机器人的完整动力学模型,并进行了相应的仿真和试验研究。为了实现对球形机器人的轨迹跟踪控制,设计了一个自适应模糊滑模变结构控制器。通过将滑模变结构控制器中的切换项进行模糊逼近,使切换项连续化,从而有效降低了抖振;对满足一定条件的参考轨迹,实现了非完整机器人系统的全局渐近轨迹跟踪控制。仿真结果证明了该控制器的有效性和正确性。
参考文献
[1] HALME A, SCHöNBERG T, WANG Y.Motion control of a spherical mobile robot[C]// International Workshop on Advanced Motion Control (AMC), 1996.259-264.
[2] JAVADI A H, MOJABI P.Introducing august: a novel strategy for an omnidirectional spherical rolling robot[C]//IEEE International Conference on Robotics and Automation, 2002:3527-3533.
[3] ZGAN Q, ZHOU T, CHEN M,et al.Dynamic trajectory planning of a spherical mobile robot[C]//IEEE International Conference on Robotics, Automation & Mechatronics (RAM), 2006:1-6.
[4] BHATTACHARYA S, AGRAWAL S K.Spherical rolling robot: A design and motion planning studies[J].IEEE Transactions on Robotics and Automation, 2000, 16(6): 835- 839.
[5] OTANI T, URAKUBO T, MAEKAWA S, et al.Position and attitude control of a spherical rolling robot equipped with a Gyro[C]//IEEE International Workshop on Advanced Motion Control (AMC), 2006:416-421.
[6] ZHAO B, LI M, YU H, et al.Dynamics and motion control of a two pendulums driven spherical robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2010.147-153.
[7] LIU D, SUN H, JIA Q.A family of spherical mobile robot: Driving ahead motion control by feedback linearization[C]//IEEE International Symposium on Systems and Control in Aerospace and Astronautics (ISSCAA), 2008.1-6.
[8] LIU B, YUE M, LIU R.Motion control of an underactuated spherical robot: A hierarchical sliding-mode approach with disturbance estimation[C]//IEEE International Conference on Mechatronics and Automation (ICMA), 2012.1804-1809.
[9] YUE M, LIU B.Adaptive control of an underactuated spherical robot with a dynamic stable equilibrium point using hierarchical sliding mode approach[J].International Journal of Adaptive Control and Signal Processing, 2014, 28(6): 523-535.
[10]KAYACAN E, RAMON H, SAEYS W.Adaptive neuro-fuzzy control of a spherical rolling robot using sliding-mode-control-theory-based online learning algorithm[J].IEEE Transactions on Cybernetics, 2013,43(1): 170-179.
[11]LIU D L, SUN H X, JIA Q X.Stabilization and path following of a spherical robot[C]//IEEE International Conference on Robotics, Automation and Mechatronics (RAM), 2008.676-682.
[12]KAYACAN E, BAYRAKTAROGLU Z Y, SAEYS W.Modeling and control of a spherical rolling robot: a decoupled dynamics approach[J].Robotica, 2012, 30(4): 671-680.
[13]GAJAMOHAN M, MERZ M, Thommen I, et al.The Cubli: A cube that can jump up and balance[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2012.3722-3727.
[14]GAJAMOHAN M, MUEHLEBACH M, WIDMER T, et al.The Cubli: A reaction wheel based 3D inverted pendulum[C]//Control Conference (ECC), 2013 European.IEEE, 2013: 268-274.
[15]CHOU J C K.Quaternion kinematic and dynamic differential equations[J].IEEE Transactions on Robotics and Automation, 1992, 8(1): 53-64.
[16]NAZARI I, HOSAINPOUR A, PITTAN F, et al.Design sliding mode controller with parallel fuzzy inference system compensator to control of robot manipulator[J].International Journal of Intelligent Systems and Applications (IJISA), 2014, 6(4): 63.
[17]陈统, 徐世杰.非合作式自主交会对接的终端接近模糊控制[J].宇航学报, 2006, 27(3): 416-421.
ModelingofSphericalRobotandResearchonRelevantControl
Abstract:A spherical robot driven by three inertia wheels is designed; the motion of robot is implemented based on the law of conservation of angular momentum.Complete dynamics model of the robot is built by using quaternion and Kane equation modeling method; the differential equations that are controlling the motion are given, thereby an adaptive fuzzy sliding mode variable structure controller is designed to implement position control of the spherical robot, of which the parameters and dynamics model are not accurate enough.In order to weaken the buffeting vibration of the system, the switching items of the sliding mode controller are fuzzy approximated to make these items continuum.The simulation and experiments of trajectory tracking show that this controller has good manifestation in the system of which the parameters are undetermined either the dynamics model is inaccurate.
Keywords:Spherical robotDynamics modelQuaternionKane equationSliding mode variable structure controlAdaptive fuzzy control
中图分类号:TH7;TP242
文献标志码:A
DOI:10.16086/j.cnki.issn 1000-0380.201606020
修改稿收到日期:2015-11-21。
第一作者王志群(1990-),男,现为北京交通大学控制科学与工程专业在读硕士研究生;主要从事移动机器人控制方向的研究。
