自平衡小车的模型分析与数据处理

胥　芳，倪紫京，占红武

(浙江工业大学 机械工程学院，浙江 杭州 310014)

自平衡小车的模型分析与数据处理

胥芳，倪紫京，占红武

(浙江工业大学 机械工程学院，浙江 杭州 310014)

摘要：以单级倒立摆为数学模型的自平衡小车，对小车模型进行了建模和分析，找出影响自平衡的参数，考虑参数在实际测量中的难易程度进一步筛选出能够实现自平衡所需要的重要参数，依据筛选出的参数确定合适的传感器.对传感器的工作原理和传输的数据进行了详细的介绍和分析，由此得出数据的处理方法.通过实际测量的数据和处理后的数据进行对比，确定了其在精度方面的可靠性，也确信了自平衡小车在移动打印领域的可行性.

关键词：自平衡车；倒立摆模型；加速度计

自平衡小车是以单级倒立摆模型为基础的，并能够在偏离平衡状态的情况下自动回到平衡位置的一种轮式机器人[1]，在各个领域都有着广泛的应用.在代步车领域，自平衡小车凭借其占用空间小，转向灵活，功耗低等特点引起了国内外不少学者的关注[2].2002瑞士联邦工业电子实验室的Felix Grasser等通过陀螺毅和光电编码器处理采集数据，研制出DSP控制的两轮移动机器人JOE[3]；同年美国SegwayLLC公司依靠陀螺仪组、倾角传感器收集数据，开发了两轮平台电动车SewwayHT[4]；2007年加州大学圣地哥亚分校使用陀螺仪和加速度计为传感器，制作了独轮自平衡机器人Unibot[5].在代步车领域，自平衡得到了十分广泛的应用.在移动打印领域，自平衡小车还未得到应用，相比于传统的台式打印机，能够实现移动打印的自平衡小车体积小，移动灵活而且便于携带，适合宿舍、办公、出差等各个场合，在移动打印领域有着非常广阔的前景.然而移动打印对精度有着较高的要求，对时间的精度要求一般能达到100 ns的级别，对于300 dpi的墨盒更是要求每12 mm打印一个点.因此，自平衡小车的平衡控制对精度也有着较高的要求.

对平衡车实现有效控制的关键是准确检测出平衡车当前的运动姿态，当平衡车出现角度偏差时，能够及时调整到平衡点[6].这依赖于控制系统对传感器采集到的数据进行处理，通过调节电机转速实现自平衡控制，这就需要精确的数据.在数据这方面，众多学者的研究角度是如何通过滤波算法提升数据精度[7-8]，很少有学者从传感数据来源这一块入手分析数据.基于陀螺仪和加速度计传感器，对加速度传感器的原理和数据来源进行了详细介绍和分析，得出合理的数据初步计算方法.最后在通过测量数据和理论数据的对比，确定了数据精度的可靠性.

1单级倒立摆模型

1.1单级倒立摆模型简介

图1为单级倒立摆的数学模型，假设模型参数：小车质量为M，摆杆长度为l，质量为m，摆杆转动惯量为J，小车与摆杆相互作用力的水平和垂直方向的分量分别为H，V.

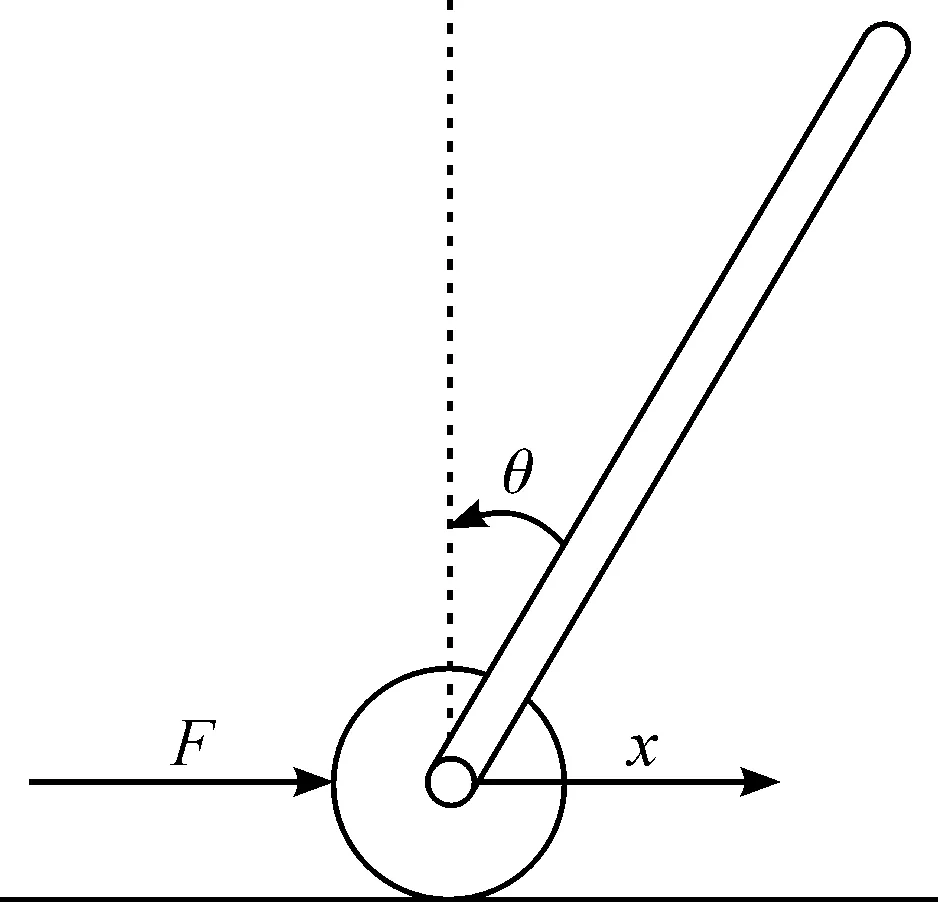
图1　单级倒立摆模型Fig.1　Single inverted pendulum model

对于摆杆，摆杆的水平位移和竖直方向上的位移分别为

xA=x+lsinθ，yA=lcosθ

(1)

那么，有

(2)

(3)

根据力矩平衡，有

(4)

结合式(2～4)，可得

(5)

对于小车，经力学分析得

(6)

结合式(2，6)，得

(7)

整理式(5，7)，可以得到

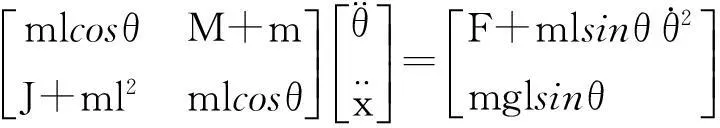
(8)

1.2单级倒立摆模型在平衡小车中的应用

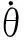
(9)

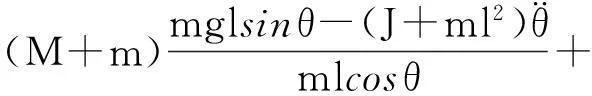
(10)

在自平衡小车中，力F主要由电机提供.结合陀螺仪后，可以避免传统的计算思路，从而大量减少计算量.然而要想使平衡小车能够实现自平衡，传感器测量的值经过一定的处理后就必须具有一定的精度，必须要正确地反映小车当时的状态.

2陀螺仪数据分析

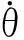
当小车静止时，加速度计输出的是灵敏轴上的重力加速度值，即重力加速度分量[9-10]，如图2所示.

图2　三轴加速度计简易示意图Fig.2　Simple diagram of three axis accelerometer

加速度计输出的值跟重力加速度之间的关系可表示为

Ay=k1gsinθ，Az=k2gcosθ

(11)其中：k1，k2分别为比例系数，结合式(11)，可以得出

(12)

MPU6050加速度计的ADC是16位，选用的量程为-4～+4g，对于需要高精度的自平衡小车来说，选择最大量程更为合理.最大量程下的分辨率为

(13)

其中：g为重力加速度，g=9.8m/s2；R为单位重力加速度下加速度计的读数，R=8 192.当MPU6050的引脚VDD接3.3V时，加速度计中的基准电压Vref=2.5V，即灵敏轴的最大输出电压为2.5V，对应小车处于平衡状态时的灵敏轴输出值；加速度计的灵敏度S=1.2V/g(加速度计中灵敏度的定义

为灵敏轴输出电压与重力加速度之比)，因此加速度计的最大计数Cmax为

(14)

将灵敏轴的最大计数按照正负区间对分，实际灵敏轴传给单片机的的数据在-8 533～+8 533之间.

3实验数据与误差分析

3.1数据收集与处理

自平衡小车的机构模型如图3所示.图3(a)中，小车的状态为理想中小车的平衡状态，此时小车和坐标之间的关系为：小车的车轮和坐标x轴同轴，z轴竖直向上.图3 (b)中，将小车倾斜一定的角度，并从左侧观测.图3(b)中的倾角θ为z轴和竖直方向的夹角，引入“数据线”是为了方便表示小车的车头与车尾.针对小车的几种特殊位置对数据进行采集，结果如表1所示.

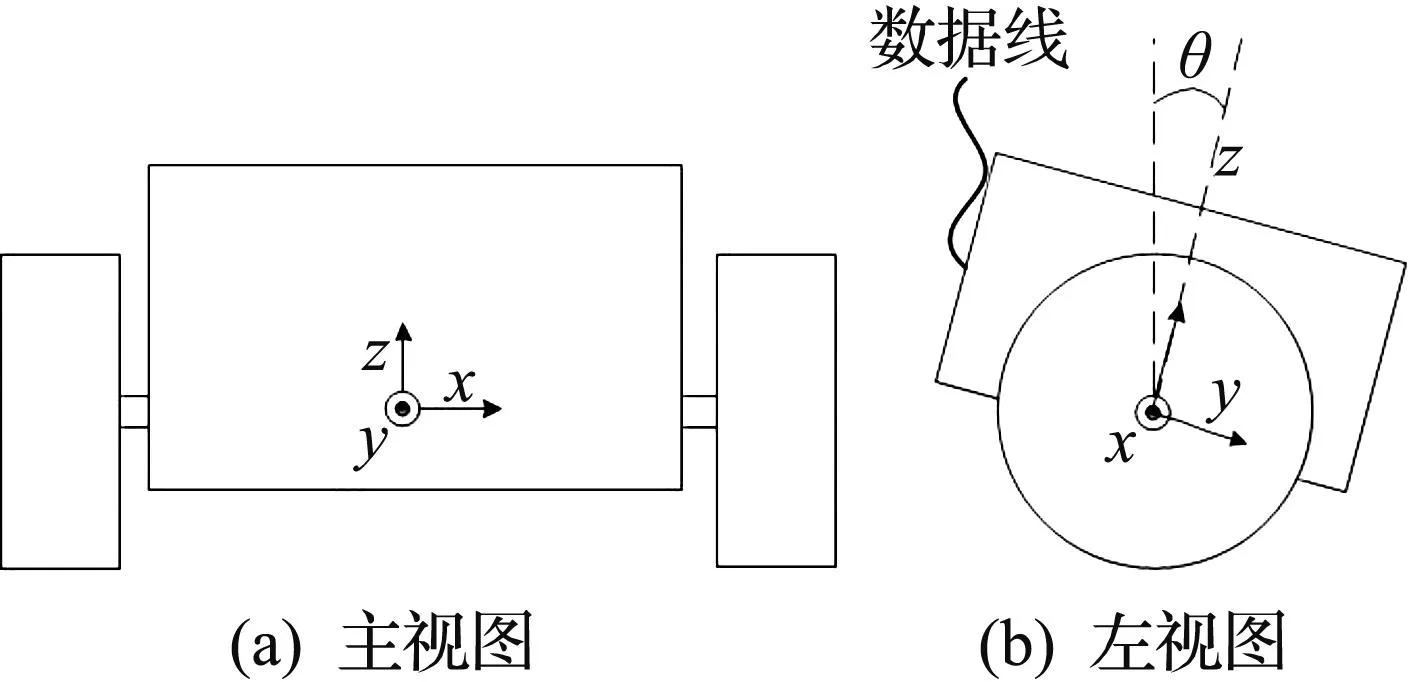
图3　小车简易视图Fig.3　Simple diagram of the car

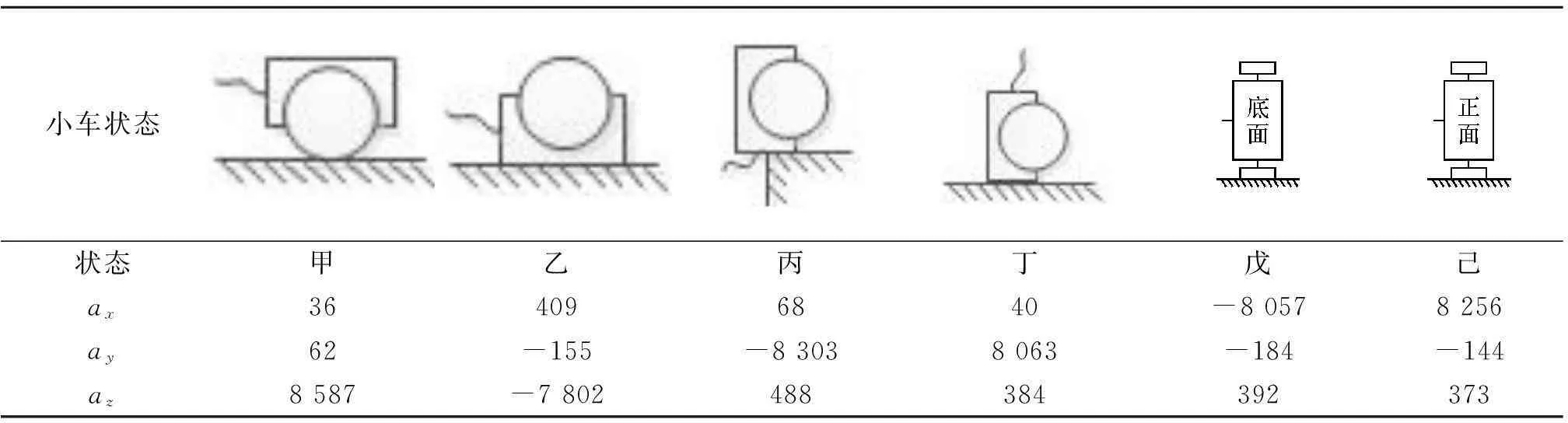
小车状态状态甲乙丙丁戊己ax364096840-80578256ay62-155-83038063-184-144az8587-7802488384392373

对于数据az，状态甲和乙的两种位置关系分别为小车在z轴上的两种极限位置，由于陀螺仪的生产工艺缺陷，两种极限状态对应的数值之和一般不为零，即零点漂移.分别观察各个轴极限位置的数据，即数据az中状态甲和状态乙，ay中状态丙和丁，ax中状态戊和己对应的数据，它们均存在不同程度的零点飘移，为防止零飘数值覆盖有效数值，引入补偿值消除零点漂移带来的误差[11-12]，分别结合状态戊和己，丙和丁，甲和乙，利用均值公式求得x,y,z轴的补偿值分别为99.5，-120，392.5.

得到补偿值后，以小车倾角为变量测得小车一般位置的数据如表2所示.

表2　小车一般位置数据表

根据式(12)，使用引入补偿值后的数据代替原先未经过处理的数据，可以得到

(15)

ax′=ax+xo，ay′=ay+yo，az′=az+zo

(16)

引入补偿值后将数据代入式(15)进行计算，得到θ，将得到的θ进行整理，得出表3数据.

表3　小车倾角对照表

3.2误差分析与结果

实际测量倾角存在一个倾角的测量误差，这个误差难以消除，但其误差范围大致可以控制在-0.5～+0.5内，在这个误差范围内，加速度计测量得出的数据通过计算后与实际测量的数据相比误差小，精度高，说明自平衡小车在移动打印领域具有一定的可行性.

4结论

从自平衡小车的基础模型出发，利用牛顿力学定律建立平衡方程，并依据传感器的测量对象求解平衡方程，确定了实现自平衡所需要的重要参数.针对需要的参数选择对应传感器并对传感器的数据来源对数据作了详细分析并测量给出在特殊状态下和一般状态下的陀螺仪相关数据.针对特殊数据求出各个轴的偏移量补偿值，并基于数据分析对数据进行相关处理.最后通过将处理后的数据和实验测量的数据进行对比，验证了传感器在精度方面能够达到要求.基于拥有足够精度的陀螺仪，平衡小车可在各个领域得到广泛使用，在移动打印领域更是具有一定的可行性.

参考文献：

[1]孙军，万明伦，吕博，等.平衡车机电控制系统建模与仿真[J].机械与电子，2010(10)：34-37.

[2]冯思远，鲁庭勇，张丽君.两轮自平衡车运动姿态的测量和控制[J].测控技术，2015，34(4)：71-74.

[3]FELIX G，ALDO D A，SILVIO C J：A mobile inverted pendulum[J]. IEEE transactions on industrial electronics，2002，49(1)：107-114.

[4]李红美，高飞.平衡的杰作—赛格威HT两轮平台电动车[J].电器工业，2002，6(1)：19-21.

[5]黄永志，陈卫东.两轮移动机器人运动控制系统的设计与实现[J].机器人，2004，26(1)：40-44.

[6]梁光胜，杜梦楠，周子豪，等.基于互补滤波的两轮自平衡车姿态控制[J].测控技术，2015，34(5)：72-74.

[7]杨凌霄，李晓阳.基于卡尔曼滤波的两轮自平衡车姿态检测方法[J].计算机仿真，2014，31(6)：406-409.

[8]边群星，成锟，陈郑洲.基于互补滤波器的两轮平衡车姿态角度测量[J].电子设计工程，2014，22(18)：55-58.

[9]徐志江,庄壮,孟利民.一种基于Android智能手机的车载定位查询软件[J].浙江工业大学学报,2013,41(6):655-659.

[10]张吉昌，程凯，郑荣儿.单轴双轮自平衡车姿态检测方案设计[J].中国海洋大学学报，2009，39(3)：467-470.

[11]孙明轩,余轩峰,孔颖.终态神经计算:有限时间收敛性与相关应用[J].浙江工业大学学报,2015,43(3):311-317.

[12]张霓,范一心,何熊熊.基于观测器的多时变时滞系统H_∞输出跟踪控制[J].浙江工业大学学报,2015,43(4):438-444.

(责任编辑：刘岩)

Model analysis and data process of the self-balance car

XU Fang, NI Zijing, ZHAN Hongwu

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:The self-balance car is built with the single inverted pendulum model. Firstly, building and analyzing the model in order to find the parameters that influence the balance, then in the consideration of difficulty in factual measure, the critical parameters which determine the balance are screened further. With those parameters, the sensors are determined. Then the theory and sensor data are analyzed and processed in detail to obtain the data deal way. Finally, by comparing the measure data and theory data, the reliability of the sensor and the feasibility of self-balance car in mobile printing are verified.

Keywords:self-balance car; single inverted pendulum; accelerometer

收稿日期：2015-12-01

基金项目：浙江省科技计划项目(2011R50011-01,2011R50011-05)

作者简介：胥芳(1964—)，女，浙江杭州人，教授，研究方向为数字印刷，E-mail: fangx@zjut.edu.cn.

中图分类号：TP272

文献标志码：A

文章编号：1006-4303(2016)03-0288-04