小量程摆式加速度计的小角度十二点翻滚测试方法
2015-07-09年海涛刘宝凤蒋效雄
吴 畏,年海涛,刘宝凤,崔 晶,蒋效雄
(1.天津航海仪器研究所,天津 300131;2.总装备部驻天津地区军事代表室,天津 300131)
0 引言
目前,以石英挠性加速度计为典型代表的摆式加速度计已得到十分广泛的应用[1-3]。摆式加速度计通常可按照国军标所介绍的十二点翻滚测试方法进行测试[4]。根据这种方法我们可将摆式加速度计安装在分度头上,分别测出0°、30°、60°、90°、 120°、 150°、 180°、 210°、 240°、 270°、300°、330°时加速度计的输出,然后通过计算,得到加速度计的偏值K0、标度因数K1、二阶非线性系数K2、三阶非线性系数K3以及输入轴和摆轴的交叉耦合系数Kip、输入轴和输出轴的交叉耦合系数Kio。在这种方法中,当分度头的读数为90°和270°时,加速度计的输入分别为 +1g和 -1g,因此加速度计的输入量程必须大于等于 ±1g,这样的加速度计在航海、船舶领域十分常见。但有些特殊用途的加速度计,为了追求某项指标的高精度,往往需要以牺牲输入量程为代价,使其量程小于 ±1g。这种加速度计显然不能直接按照国军标所介绍的十二点翻滚测试方法进行测试。为了解决这一问题,在深入分析常规十二点翻滚测试基本原理的基础上,对其进行了适当修改,从而提出了一种能够适用于小量程摆式加速度计的小角度十二点翻滚测试方法。
1 小角度十二点测试方法
1.1 安装状态定义
在讨论原理之前,有必要先对摆式加速度计的坐标系进行说明。加速度计的坐标轴分别为输入轴、输出轴和摆轴,这三个轴两两垂直。
在分度头上进行加速度计测试时需要将分度头的回转轴调节到水平方向。加速度计在分度头上的安装方式有摆态和门态两种,在摆态,加速度计的输出轴平行于分度头的回转轴;而在门态则是摆轴平行于分度头的回转轴。不论哪一种安装方式,分度头转角θ=0°都是对应于输入轴处于水平方向,此时若为摆态,则摆轴垂直向下;而若为门态,则输出轴垂直向下。当分度头转角θ=90°时,不论摆态还是门态,输入轴的正方向都是垂直向上的。面向分度头的安装盘面,若所使用的分度头安装盘面顺时针转动时角度读数增大,则在两种安装方式下,初始位置时加速度计各轴的指向分别如图1(a)和图1(b)所示。

图1 面向分度头盘面观察时加速度计各轴初始方向示意图Fig.1 Schematic illustration of the initial directions of the accelerometer axes which are observed by facing the dividing head plate
1.2 模型方程
加速度计在地球重力场测试中的静态数学模型方程如式 (1)所示。

其中,E为加速度计的输出,单位为输出单位;K1为标度因数,单位为输出单位 /g;K0为偏值,单位为 g;K2为二阶非线性系数,单位为g/g2;K3为三阶非线性系数,单位为g/g3;δo、δp分别为输入轴绕输出轴和摆轴相对于输入轴的安装误差角,单位为rad;Kip为输入轴和摆轴的交叉耦合系数,单位为g/g2;Kio为输入轴和输出轴的交叉耦合系数,单位为g/g2;ai、ap和ao分别为输入加速度沿输入轴、摆轴和输出轴的分量,单位为g。
对式 (1)中模型的各项系数值进行测试时,常规方法是将加速度计安装在分度头 (或精密端齿盘)上,绕水平轴沿360°旋转。这要求加速度计的量程不小于±1g。对于量程小于 ±1g的加速度计,只能根据量程大小,在0°位置 (0g)和180°(-0g)位置的附近角度内来回转动,利用重力加速度的分量作为输入加速度,来对加速度计的数学模型系数进行标定。
由于加速度计在测试的过程中,不可避免地要受到地基振动、环境噪声、温度漂移等因素的影响,为了尽可能准确地测量模型系数,减小测量误差,在加速度计量程范围内,对称地选取12个位置点,根据该位置处重力加速度计的分量(输入加速度值)和加速度计的输出值,按照最小二乘法进行拟合,计算出加速度计数学模型的各项系数。用这种方法测量出的模型系数值与理论值之间的标准差最小,模型系数的实测值最接近理论值。
1.3 原理分析
首先,对不同位置时各轴上的加速度分量进行分析。将重力加速度及其分量作为加速度计的输入加速度,由图1(a)易得出,摆态下,重力加速度g在加速度计各轴的分量与分度头转角θ(初始位置为0°)之间的关系为:

根据加速度计的量程,选取适当的分度头转角θ,在12个位置进行小角度十二点翻滚测试,测出各个位置时加速度计的输出Ei(i=1,2,…,n;n=12,分别对应θ值由小到大的12个位置)。这时,加速度计的模型方程将取如式 (2)所示。
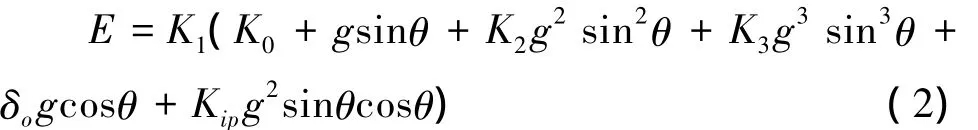
对三角函数进行变换并化简,得到

而加速度计输出E的傅氏级数形式可写为[5]

比较傅里叶系数可得:
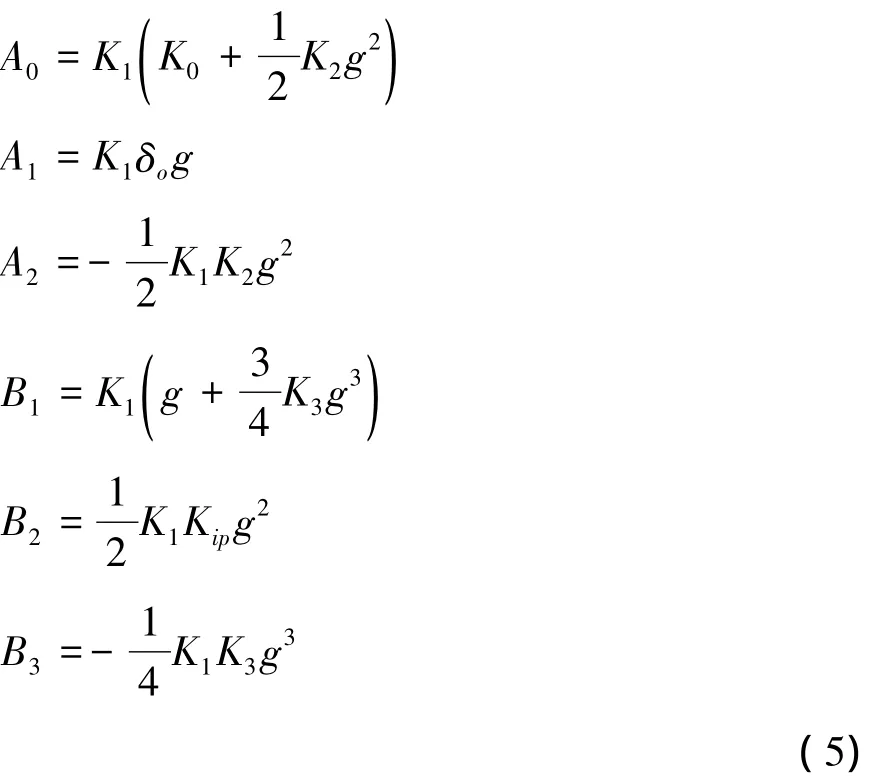
于是可以解得加速度计的模型方程系数见式(6)。


则在分度头转角不同位置处的傅氏级数为
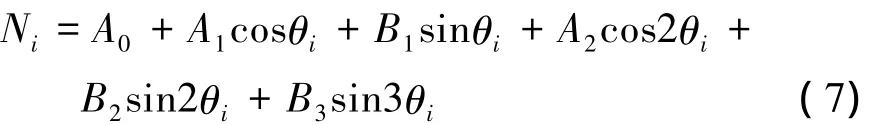
利用最小二乘法,在各个分度头角度设定处,辨识模型输出与测试输出的偏差平方和为

对每个参数取偏导数,并使它们等于零,则所得方程组的矩阵形式为
变换矩阵得到

根据加速度计在各位置的输出电压,利用该矩阵即可计算出傅氏展开的各个系数,进而可以得到偏值K0,标度因数K1,二阶、三阶非线性系数K2、K3,输入轴安装误差角δo,输入轴和摆轴的交叉耦合系数Kip。至于门状态下输入轴安装误差角δp和输入轴相对于输出轴的交叉耦合系数Kio,则需要在门状态下的十二点翻滚测试方法中进一步得到。
在门状态,由图1(b)很容易看出,值为1g的重力加速度在加速度计各轴的分量与分度头转角θ之间的关系为:

在门状态下的小角度十二点翻滚测试,可以求得摆态下所不能得到的输入轴安装误差角δp和输入轴与输出轴的交叉耦合系数Kio。于是我们通过摆态和门态两种方式的小角度十二点测试,可以得到加速度计数学模型的全部待定系数:偏值K0,标度因数K1,二阶、三阶非线性系数K2、K3,输入轴安装误差角 δo、δp, 输入轴和摆轴、输入轴和输出轴的交叉耦合系数Kip、Kio。
2 方法验证
2.1 仿真分析
为了验证小角度十二点翻滚测试方法测量加速度计模型系数的准确性,仿真计算加速度计在分度头处于不同位置时的输出信号,并人为加入一组随机误差作为噪声,分别采用国军标十二点和小角度十二点翻滚测试方法计算加速度计的模型方程,看两种测试方法计算出的加速度计模型系数差别是否明显。
以加速度计在摆态下为例,首先,假定加速度计模型系数的值:

根据式 (2)可以计算出加速度计在分度头每个位置处的输出信号的理论值。人为引入一组期望值为0、方差和标准差均为1并成正态分布的随机信号Ri(i=1,2,…,12),考虑到实际噪声的幅值,选取Ri(i=1,2,…,12)/107作为加速度计的噪声[6],那么加速度计的模型方程变为式(13)。

其中:i=1,2,…,12。
根据加速度计的输入加速度和输出信号Ei,分别利用国军标十二点和小角度十二点翻滚测试方法仿真计算加速度计的模型系数,不同步长a情况下仿真结果如表1所示。
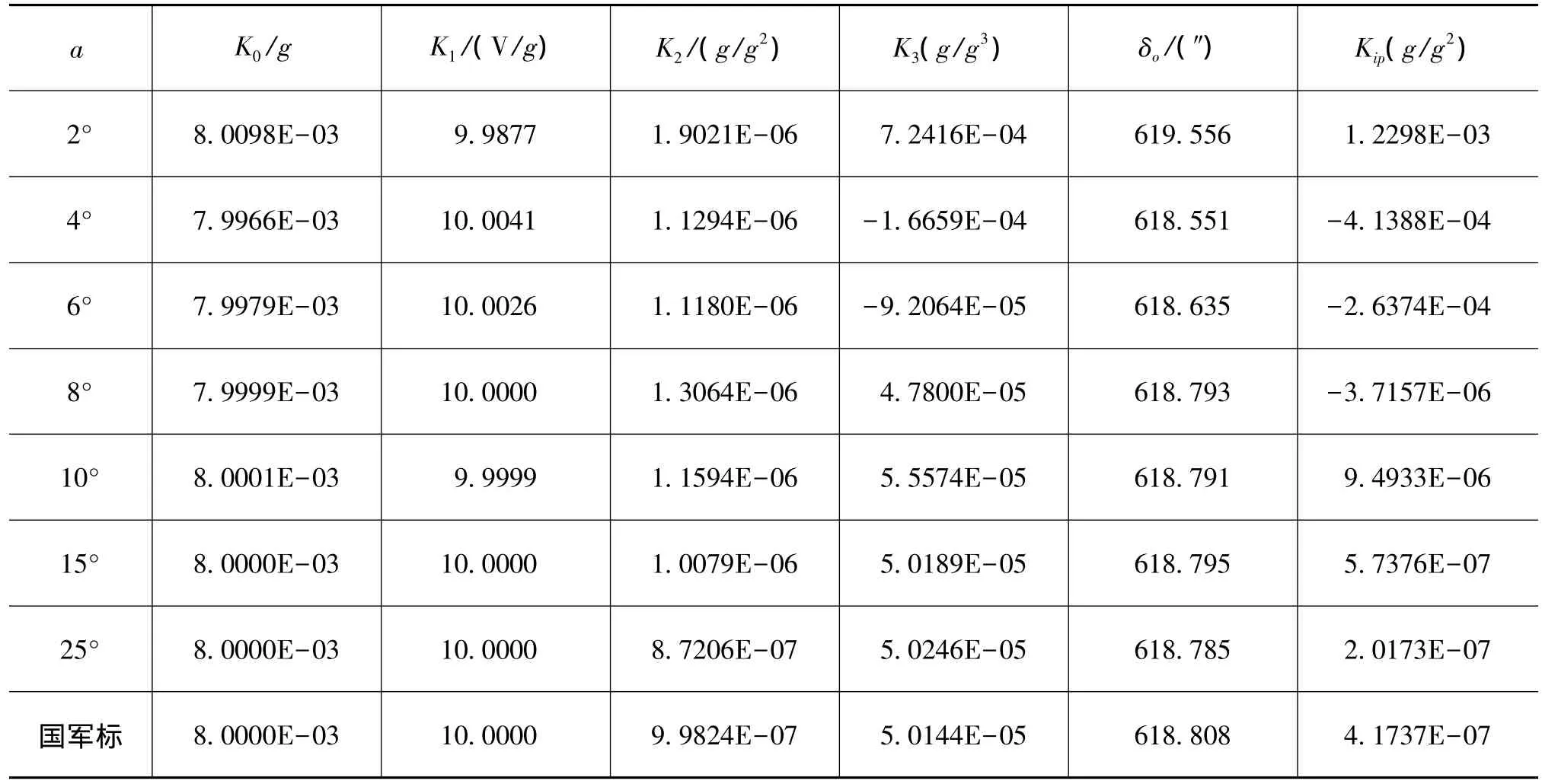
表1 不同步长a值时加速度计仿真结果Tab.1 Simulation data of accelerometer with different values of a
从仿真结果可知,小角度十二点法跟国军标十二点法一样,可以比较准确地标定加速度计的模型系数,其中偏值K0、标度因数K1和输入轴安装误差角δo(门态为δp)的值与国军标测出的系数值误差均小于1.5‰;二阶非线性系数K2在a≥4°时与国军标系数的误差小于13%;三阶非线性系数K3和交叉耦合系数Kip(门态为Kio)有一定误差,这是由于加速度计在小角度时对高次项和交叉耦合项不如大角度敏感 (加速度计的交叉耦合项在45°时最敏感[7])。
2.2 测试结果
运用小角度十二点翻滚测试方法测试某摆式加速度计,从转台的0°开始,步长为a,先沿顺时针方向转动12个角位置,再沿逆时针方向转动到这12个角位置,依次测量每个位置的加速度计输出值。考虑到小量程加速度计基本都工作在0°位置,为了尽可能准确地反映加速度计的输出情况,围绕0°对称地选取10个小角度位置点,再加上0°和180°,得到小角度十二点翻滚的12个位置:0°、0°+a、0°+2a、0°+3a、0°+4a、0°+5a、180°、360°- 5a、360°- 4a、360°- 3a、360°-2a、360°-a(以a=2°为例,则这12个位置依次为 0°、2°、4°、6°、8°、10°、180°、350°、352°、354°、356°、358°)。
以加速度计在摆态下为例,分别选取不同的步长a值,得到加速度计模型系数的测试结果如表2所示。
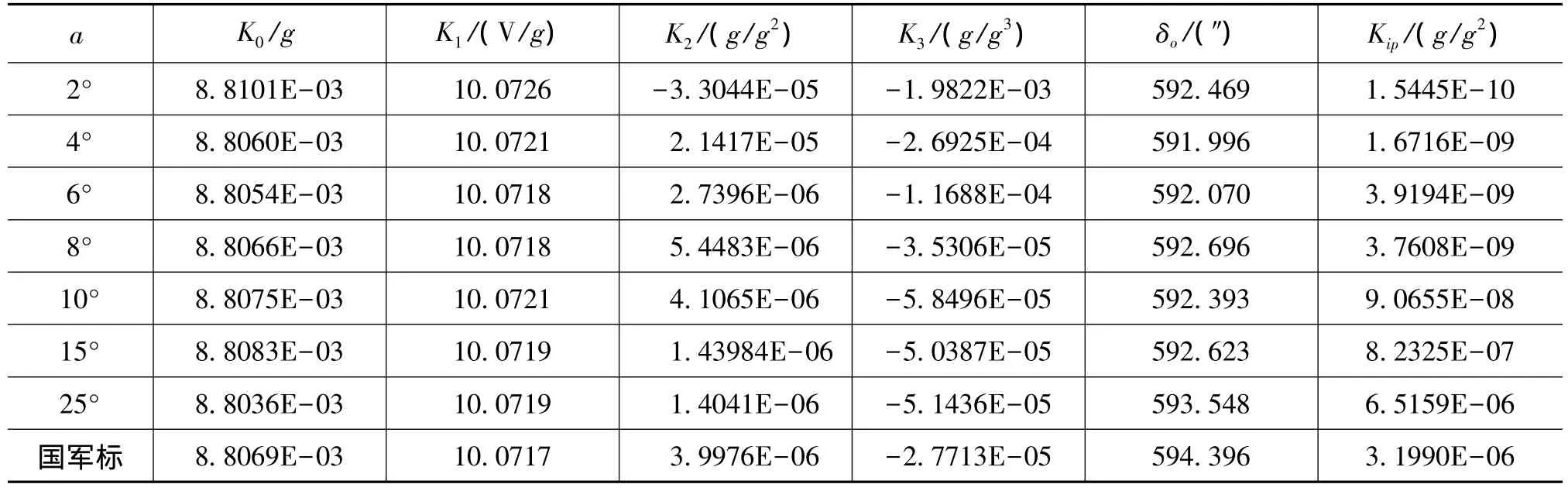
表2 不同步长a值时加速度计标定结果Tab.2 Test data of accelerometer with different values of a
测试结果与理论仿真结果一致,偏值K0、标度因数K1和输入轴安装误差角δo的值与国军标测出的系数值的误差分别为 0.36‰、0.09‰和3.24‰。证明小角度十二点翻滚测试方法能够通过测试零位附近位置的加速度计输出,来计算加速度计的模型系数。
根据不同步长下12个位置的最大加速度值,可以确定不同量程加速度计应该选取的步长a值,如表3所示。

表3 不同量程加速度计对应的步长a值Tab.3 Values of a of accelerometers with different ranges
3 结论
针对由于某些特殊原因量程小于 ±1g范围的加速度计,提出了小角度十二点翻滚测试法,通过测试加速度计零位附近角度处的输出来标定加速度计的模型方程。首先分析了小角度翻滚测试的原理,然后给出了模型系数计算公式,利用该公式进行了理论仿真研究,并按照此方法进行了实际测试,得出了可靠的测试结果,确定了加速度计量程与步长的关系,为小量程摆式加速度计的测试提出了一种可行的方法。
但是,对于小角度十二点翻滚测试过程中,转台的定位误差相对较大的问题,尚无可行的解决方法,有待进一步的研究。
[1]吴书朝.小量程摆式加速度计的小角度四点翻滚测试方法[C]//.中国惯性技术学会第六届学术年会论文集,2008,11:398-402.
[2]Anthony Lawrence.Modern inertial technology[M].Navigation,Guidance,and Control,1993:57-71.
[3]Foote S A,Grindeland D B.Model QA3000 Q-Flex accelerometer high performance testresults[C]//.Aerospace and Electronic Systems Magazine,IEEE,1992,7(6):59-67.
[4]GJB 1037A-2004.单轴摆式伺服线加速度计试验方法[S].
[5]王大千,张英敏.加速度计1g重力场静态翻滚测试与误差分析[J].机械与电子,2009,(1):34-36.
[6]许伟,李强,陈冬雪,等.基于小波降噪与最小二乘估计的石英挠性加速度计模型辨识[J].传感技术学报,2013,26(11):1493-1498.
[7]孙枫,曹通.基于Kalman滤波的加速度计十位置标定方法[J].系统工程与电子技术,2011,33(10):2272-2276.
