大豆期货合约均值回归套利策略和Elman神经网络套利策略对比研究
2016-06-28刘建和梁仁方王玉斌
刘建和 梁仁方 王玉斌 吴 伟
(1. 浙江财经大学 金融学院,浙江 杭州 310018;2. 中国农业大学 经济管理学院,北京 100193;3. 永安期货研究所,浙江 杭州 310005)
大豆期货合约均值回归套利策略和Elman神经网络套利策略对比研究
刘建和1梁仁方1王玉斌2吴伟3
(1. 浙江财经大学 金融学院,浙江 杭州310018;2. 中国农业大学 经济管理学院,北京 100193;3. 永安期货研究所,浙江 杭州310005)
【摘要】国内压榨市场大豆主要来源于国外进口,并且国内压榨市场缺乏对大豆价格制定的主导权,故可通过大豆及其压榨品豆粕、豆油进行跨商品套利。综合运用协整检验、误差修正模型(ECM)研究大豆、豆粕、豆油三者价格之间长期存在的相互关系,同时通过设置不同开平仓阀值,对比均值回归模型套利策略和Elman神经网络模型套利策略,实证结果表明:我国大豆期货及豆粕和豆油期货三者进行跨商品套利可行,能够获得正向的套利收益率;在不同的开平仓阀值下,Elman神经网络模型较均值回归模型能够得到更好的套利结果。
【关键词】大豆期货;套利策略;均值回归法;Elman神经网络法
一、引言
2014年我国大豆进口总量达到7140万吨,首次突破7000万吨,同比增加12.7%。相对于国内1200万吨的大豆产量,进口大豆占据了国内大豆市场的85.61%。按照目前法律、法规要求,进口大豆必须全部用于压榨。CBOT是全球大豆定价中心,国内大豆进口企业主要是采取在CBOT点价的方式进行进口贸易。因此,国内大豆压榨市场对国际大豆价格依赖性较强,极大地限制了国内压榨企业的发展[1]。从我国进口大豆的历史情况看,大豆进口成本呈逐渐增加态势。1998-2002年平均为2200元/吨,2003-2007年平均为3000元/吨,2008-2011年平均为4150元/吨,2012-2014年平均为4442元/吨,出现了4次“尖峰”。但每次大豆价格“尖峰”都预示着大豆行情震荡,国内压榨企业由于缺乏大豆定价权,大豆价格频繁的波动给企业带来了巨大损失。
大豆期货是中国商品期货品种中上市早、持续交易时间长、累计交易量最大的品种,也是交易最规范和成熟的品种之一。从1993年挂牌至2008年年底,大连大豆期货合约累计成交量、成交额分别为9.9亿手、30.9万亿元,占大连商品交易所累计成交量、成交额的45.72%和45.97%[2]。按照FIA全球农产品期货期权成交量排名,2008年大连商品交易所大豆期货在全球前20个农产品中位居第二,成为全球第二大大豆期货交易市场。值得注意的是,Liu et al.(2015)的研究表明我国大连豆一期货的价格波动已经有一定独立性,受到海外大豆期货的影响越来越小,也就是说,我国大豆期货市场在全球范围内的地位越来越高[3]。
对我国大豆期货的研究有利于大豆及大豆压榨相关行业和企业规避大豆价格波动风险,我国大豆期货现有的地位也有利于以期货公司为代表的实务界和以期货私募基金为代表的投资界研究其套利策略,获得超额收益。但从现有关于大豆期货及其压榨品豆粕、豆油期货套利的研究成果看,其一,关于大豆跨商品套利的成果并不多见,而且这些不多的成果主要是针对CBOT美豆进行套利的实证研究,对我国大豆期货进行套利策略研究的成果较少;其二,从跨商品套利策略看,绝大部分成果都是针对大豆期货和豆粕期货或者大豆期货和豆油期货进行双品种的套利策略研究,对于三类期货品种同时进行跨商品套利策略研究并不多见;其三,国内学者对于大豆及其压榨品豆粕和豆油的期货套利研究缺乏对其进行实证套利策略的操作研究。现有文献仅有顾全和雷星晖(2015)进行了实物套利研究,而且他们也只是利用了传统的均值回归法进行研究[4]。因此,笔者利用Elman神经网络模型,选择我国大豆期货、豆粕期货和豆油期货三者同时进行跨商品套利策略的实证研究,并利用均值回归模型套利策略进行对比。笔者希望能够通过此研究弥补国内大豆期货套利研究的不足,也希望为实务界和投资界对大豆期货的套利策略提供实证参考。笔者的实证结果表明:第一,我国大豆期货及其豆粕和豆油期货三者进行跨商品套利可行,能够获得正向的套利收益率;第二,Elman神经网络套利策略强于传统的均值回归套利策略。正是如此,期货私募基金等投资者可以利用神经网络套利策略进行大豆期货、豆粕期货和豆油期货三者的跨商品套利获得正向收益,海内外期货投资者也有必要将我国大豆及其相关期货纳入到其期货投资组合中。
二、理论综述
期货套利主要可以分为跨交割月份套利、跨市场套利和跨商品套利三大类。以跨商品套利为例,就套利方法而言,可以把相关研究划分为传统的均值回归套利方法和神经网络套利方法两大类。
1、均值回归套利方法
均值回归套利方法是通过金融时间序列计量方法如协整、误差修正模型(ECM)、回归等来分析商品期货之间长期存在的相互关系,从而设计其中的套利策略。比如,Simon(1999)利用协整检验等实证分析方法,证明大豆压榨价差存在长期均值关系,并且具有明显的季节性特征[5];Liu(2005)利用协整方法对生猪、玉米、豆粕价格进行实证,发现三者之间存在长期均值关系,并且交易模拟也证实了获利的可能性[6]; Han、Liang和Tang(2013)运用结构向量自回归模型和向量误差修正模型对CBOT和DCE大豆商品进行跨市场套利研究,实证结果表明DCE大豆商品期货价格能够长期影响到CBOT大豆商品期货价格,投资者可以进行跨市场套利[7]。国内学者如杨升等(2008)借助ADF单位根检验方法及协整理论对大连商品交易所豆一与豆粕期货合约价格进行了实证研究和分析,发现上述两交易品种期货合约价格之间存在协整关系[8];顾全和雷星晖(2015)选取大连商品交易所大豆、豆粕和豆油期货主力合约2006年至2012年收盘价为研究对象,对价格序列进行协整检验,以此为基础建立误差修正模型(ECM),发现三者之间可以利用均值回归模型进行套利[4]。
2、神经网络套利方法
神经网络套利方法在于运用神经网络模型对期货价格进行预测从而制定套利策略。如Hornik等(1989)运用神经网络模型对大豆压榨价差的短期波动进行预测,并且达到了一定的精确性[9];Dunis、Jason和Ben(2006)运用多层感知模型(MLP)、递归神经网络模型(RNN)、高级神经网络模型(HONN)来分析大豆、豆油价差的短期波动,通过相关性滤波筛选后,套利效益明显提升[10];Wiles和Enke(2014)运用RBF神经网络、LM神经网络对大豆及其压榨品豆粕、豆油价差的短期波动进行分析预测,认为交易者可以根据远期合约影响近期合约压榨价差利润这一现象进行套利[11]。目前国内学者如王中香、王风和何穗(2009)[12],孙海涛、杨德平和李聪(2012)[13],以及徐颢华和顾海峰(2014)[14]对神经网络套利方法的应用进行了研究,不过前者研究黄金期货套利策略,后二者主要研究股指期货套利策略。国内应用神经网络套利法研究大豆期货套利策略的研究成果尚不多见。
3、简单评述
总体上,从国内对大豆期货的套利策略研究成果来看,首先,对大豆期货跨商品套利策略的研究主要集中在大豆和豆粕或者大豆和豆油之间两个品种之间的套利,对大豆、豆粕和豆油期货三个品种同时进行套利策略研究的成果不多见;其次,对套利方法的应用主要集中在传统的均值回归套利上,对神经网络模型的应用并不多见;再次,即使以神经网络应用到其他期货品种的研究上来看,这些成果主要使用BP神经网络模型,对其他神经网络模型的应用并不多见;最后,现有的绝大部分研究成果主要集中于单一模型期货套利策略,缺乏不同套利方法的策略对比,投资者难以选择有效的策略进行期货套利。所以,笔者借助计量分析方法,通过协整检验、误差修正模型(ECM)等方面研究大豆、豆粕、豆油三者价格之间长期存在的相互关系,然后通过设置不同的开平仓阀值,运用均值回归模型套利策略和Elman神经网络模型套利策略分别在样本区间内和样本区间外进行套利策略的对比研究。
三、数据处理
选取大连商品交易所豆一、豆粕和豆油合约作为研究对象。从历史数据来看,每年1月合约、5月合约和9月合约的持仓量和交易量都较大,资金参与度较高,当价格出现不合理时,市场有足够的流动性让产业资金参与发现真实的价格。在同一个交易日会存在多个合约进行交易,因此笔者需要选择用在选定时间内成交量和持仓量最高的合约来构建期货连续价格数据。在实际的期货交易中,合约的持仓量与成交量往往在交割月的前一个月就会大幅减少。因此,笔者选择在交割月前一月的第一交易日开始换月,即采用下一个主力合约的交易数据。根据以上原则,笔者选择利用每年1、5、9月份交割的合约收盘价来构建价格序列,包含了自0709合约起到1401合约结束的共1589个数据。为了对套利策略进行分析,笔者将样本区间划分成样本区间内区间和样本区间外区间。样本区间内区间为2007年5月到2013年7月共1509个数据,用于协整关系的检验和套利模型估计;样本区间外区间包含了依据前文原则构建的1401合约的80组价格数据,时间跨度为2013年8月1日起到2013年11月29日结束,用于对套利策略的样本区间外评判。
在论证大豆、豆粕和豆油之间的协整关系之前,笔者使用ADF的方法来对期货价格数据以及其差分进行单位根检验,大豆、豆粕和豆油的一阶差分分别表示成Δsoybean、Δsoymeal和Δsoyoil。从ADF检验的结果来看,soybean、soyoil和soybean价格数据的检验统计量大于1%、5%和10%检验水平临界值,可以认为以上三个序列都包含单位根,是非平稳序列;而Δsoybean、Δsoymeal和Δsoyoil的ADF检验统计量都小于1%检验水平下的临界值,因此该差分序列不包含单位根,是平稳序列,满足协整检验的条件。进一步进行协整检验,在设置滞后项数为4的情况下,大豆、豆粕和豆油期货价格之间在5%的置信水平下存在协整关系。因此尽管短期价差可能会出现偏差,但是内在的动力会驱使其回归均值,可利用均值回归策略进行三者的跨商品期货套利研究。
1、误差修正模型
通过协整检验可以发现大豆、豆粕和豆油期货价格序列之间存在长期协整关系,而这种长期协整关系是通过短期内的不断动态调整实现的,笔者参考Simon(1999)的方法来对短期动态调整的过程进行估计[5]。
首先建立回归方程:
soybeant=β0+β1soymealt+β2soyoilt+εt
(1)
对公式(1)进行OLS方法估计,得到公式(2):
soybeant=408.4453+0.8318soymealt+0.1356soyoilt
(2)
(0.0000)(0.0000)(0.0000)
R2=0.725196,F=1987.139,括号里的数字为伴随概率。从各系数的伴随概率和模型的R2来看,模型的拟合效果比较理想。
根据公式(2)可以得到其残差序列εt如公式(3)所示。
εt=soybeant-408.4453-0.8318soymealt-0.1356soyoilt
(3)
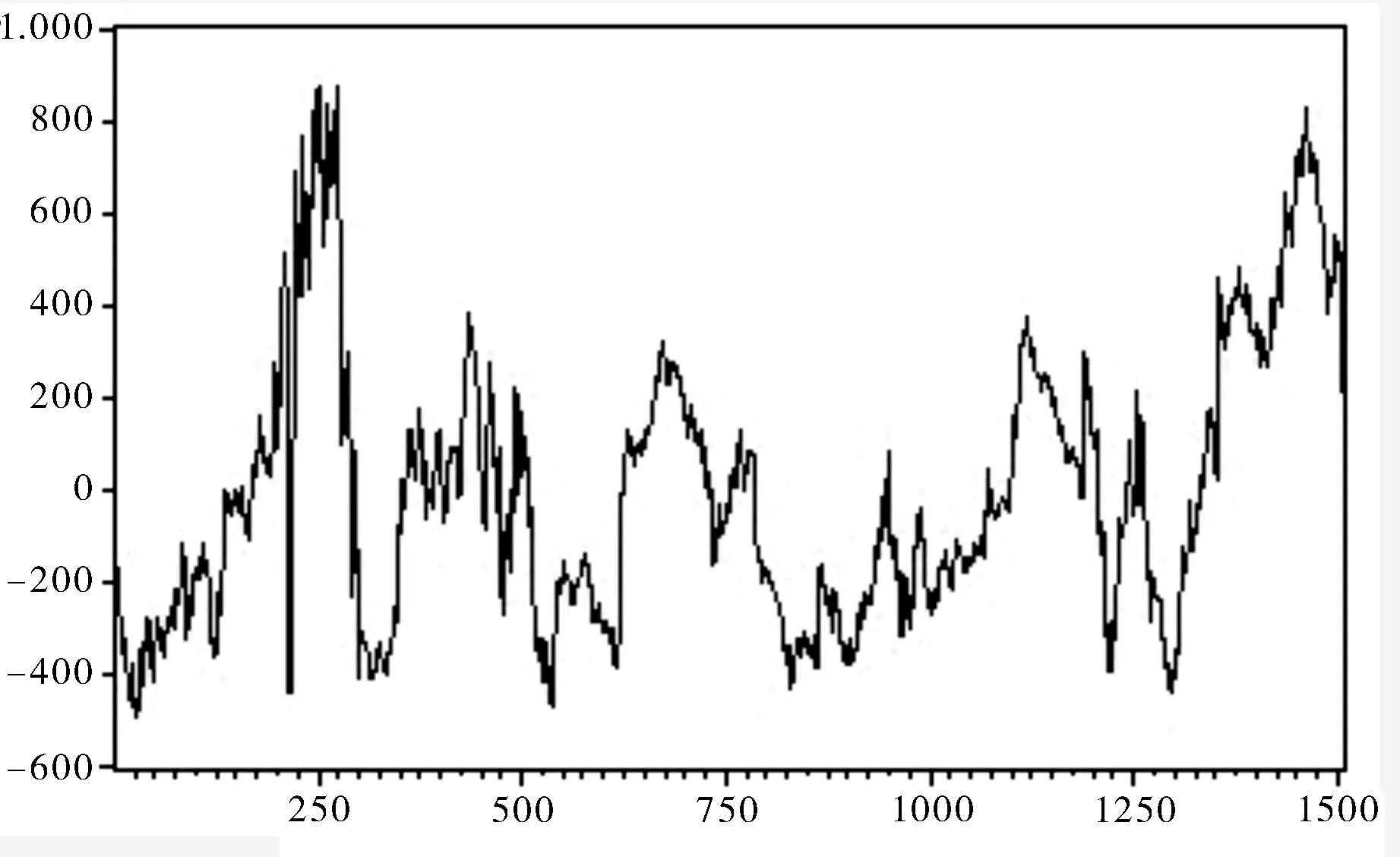
图1 大豆、豆粕和豆油货价格序列回归残差图
公式(3)给出了εt的表达形式,令:
profitt=-εt
(4)
用Δprofitt来表示压榨利润预估值的一阶差分,即压榨利润下一时刻的变化值:
Δprofitt=λprofitt-1+εt
(5)
进行最小二乘法参数估计得到:
Δprofitt=-0.016269profitt-1+εt
(6)
(0.0005)
公式(6)的结果表明profitt-1前的系数显著小于0,压榨利润存在均值回归的特征,与此同时λ还反映了短期偏差后向长期均值动态调整的过程,误差修正系数γ等于-0.016269,即前一次的非长期均值偏差会以1.62%的比例进行反向修正。笔者根据Madhavan和Smidt(1991)[15]提出的半周期公式T/2=|ln(1+λ)|,短期偏差回复至长期均值的半周期需要42天,这一数据对套利策略具有重要参考意义,因此在制定套利方案时一定要考虑这点。
2、套利头寸选择及方法
(1)套利头寸选择
在对大豆压榨套利进行分析时,选择根据长期协整公式推导出的压榨公式来进行期货品种的配比。soybean、soyoil和soybean的压榨收益可以表示成:
profitt=408.4453+0.8318soymealt+0.1356soyoilt-soybeant
(7)
由于profit的期望值已经为零,所以无需对其进行中心化处理。
笔者将依据各类策略方法来对profit头寸进行交易,其依据的核心逻辑即三者之间的长期均值关系。一份完整的profit多头头寸是买入0.8318份豆粕合约、0.1356份豆油合约,同时卖出1份大豆合约;一份profit空头头寸等于卖出0.8318份豆粕合约以及0.1356份豆油期货,同时买入1份大豆合约。
(2)交易保证金
大连商品交易所对于大豆、豆粕和豆油规定的最低保证金都为5%,经过实际调研,规定大豆、豆油和豆油的保证金比例为7%。
(3)交易费用
大连商品交易所对大豆、豆粕和豆油的交易采取固定手续费。根据实际调研,想要构建1手大豆、0.8318手豆粕和0.1356手豆油的头寸大约需要20元的手续费,而进行一次完整的买卖操作则需要计入两份手续费,即40元/手。由于是以吨为计量单位对价格进行分析,因此根据一手10吨的换算公式,总共需要的手续费计为4元/吨。
虽然大豆、豆粕和豆油期货的最后交易日都为交割月的第十个交易日,但是由于数据样本考虑的是交割月前一个月第一个交易日更换合约,因此规定最后交易日为交易合约交割月前两个月最后一天,如果价差在最后交易日仍未回归,实行强制平仓操作。
四、套利策略
1、均值回归模型套利策略
由前面的长期协整检验可知,大豆、豆粕和豆油期货之间存在长期均值关系,虽然三者的价差会存在短期偏差,但其内在关系会充当一只“看不见的手”的角色使其重新走向长期均值。因此,当profit大于一定阀值时,则表示相对豆粕和豆油的期货价格,大豆期货价格已经在一定程度上被低估,这时可以进行卖出0.8318份豆粕合约、0.1356份豆油合约,买入1份大豆合约的操作;当profit小于一定阀值时,则表示大豆期货价格已经被高估,此时可以买入0.8318份豆粕合约、0.1356份豆油期货并卖出1份大豆合约。
(1)均值回归模型开平仓信号
设X、K分别为交易的开仓阀值和平仓阀值,具体的开平仓规则如下:
第一,当|profit|>X时,进行profit套利开仓操作:如果profit>X,则进行卖出profit套利;如果profit<-X,则进行买入profit套利。
第二,当|profit|
对于X值与K值的选择,笔者将基于VAR来计算,经计算profit的标准差为292.84,由于使用的样本数据较多,因此在计算置信区间时可以参考正态分布,在80%的置信水平下进行双侧的选取来确定开仓阀值X,查表可得到|X|=292.84×1.281=375.13。所以,当profit>375.13时,进行卖出profit套利;当profit<-375.13时,进行买入profit套利。由前文可知我国大豆期货套利回归周期较长,如果选择等待短期偏差回归到长期均值状态再平仓,很有可能会面临最后不能回归的风险,因此选择在头寸自开仓阀值点向有利方向运行100个点后就平仓。即将K值设为275.13,如果持有profit空头头寸,当profit<275.13时平仓;如果持有头寸为profit多头,那么当profit>-275.13时进行平仓操作。
一日,灯草老爹来找琵琶仙。灯草老爹是张乾的结义兄弟,在河东烧窑。几天前,汉奸刁德恒带着保安队,耀武扬威地找到河东,限他五天之内烧好三窑瓦。“烧好了,皇军有赏;若有半点闪失,提头来见!”灯草老爹是个怕事的人,当下就满口答应了。场子里备有几垅干瓦坯子,烧三孔不成问题。
(2)交易时间控制
根据误差修正模型计算的回归半周期显示,profit价差由短期偏差向长期均值回归需要42个交易日,回归周期非常长。为了尽量规避最后交易日价差仍未回归的风险,规定在交割月前两个月的第一个交易日起,即使模型提供非常强烈的交易信号也不进行开仓操作。
(3)样本区间内实证结果分析

表1 基于均值回归模型样本区间内套利交易情况
注:总收益率=总收益/最高保证金
基于上述的交易原则,由表1可知,在样本区间内一共发生了11次交易。在十一次交易中,最长的持有期高达76个交易日,平均持有期为32.45个交易日,交易成本为44元,收益率为22.70%。
(4)样本区间外实证结果检验
对2013年8月1日至2013年11月29日的80个数据进行样本区间外检验,其包含了构建规则下的所有1401合约数据。由表2可知,样本区间外仅发生了一次交易,价差最终回归到长期均值状态,没有发生合约到期仍未回归导致的强行平仓。
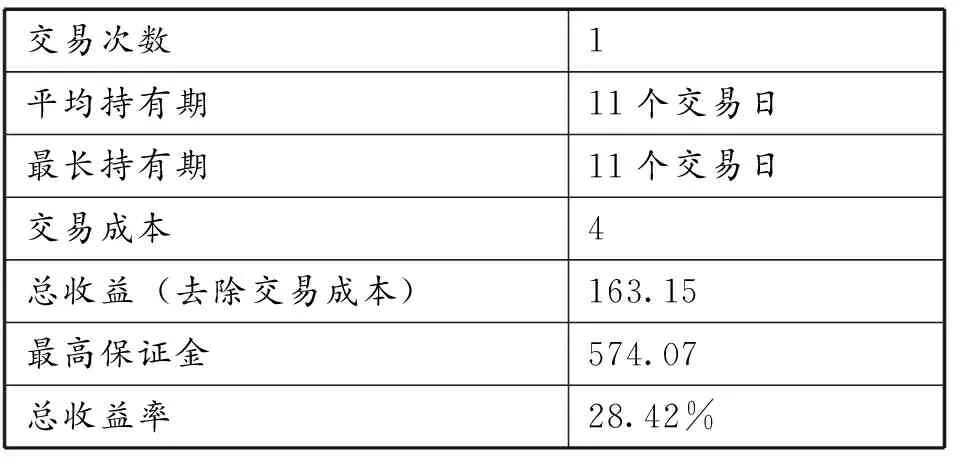
表2 基于均值回归模型样本区间外套利交易情况
2、Elman神经网络模型套利策略
(1)Elman神经网络
神经网络按照是否存在反馈与记忆可以分为静态神经网络和动态神经网络。常见的BP神经网络是一种静态神经网络。动态神经网络带有反馈与记忆功能,通过反馈与记忆,神经网络能将前一时刻的数据保留,使其加入到下一时刻数据的计算,使网络不仅具有动态性而且保留的系统信息也更加完整,如Elman神经网络。区别于BP模型,Elman神经网络除了输入层、隐藏层和输出层外,还拥有独特的承接层。承接层实质上是在隐含层的输入输出之间增加了一个延时模块,该模块延时存储了隐含层的输出信号,再作为输入变量影响隐含层的下期输入。这使得网络的输出量不仅受到当期输入量的影响,还与前一时刻的网络输出量有关,通过延时存储,Elman神经网络具有了适应时间变量的特性,被广泛应用于金融时间序列的动态研究中。
Elman神经网络模型的结构图如图2所示:
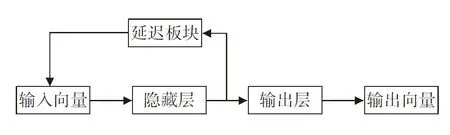
图2 Elman神经网络结构
Elman神经网络的传导过程可以用公式(8)到公式(10)来表达。
xc(t)=x(t-1)
(8)
x(t)=f1(w1xc(t)+w2(u(t-1)))
(9)
y(t)=f2(w3x(t))
(10)
上述公式中,w1、w2、w3分别代表了承接层到隐藏层、输入层到隐藏层和隐藏层到输出层之间的连接权重。u是a维输入向量,x为b维隐藏层输出向量,xc是b维承接层输出向量,y为c纬输出层输出向量。f1(.)代表了隐藏层的激励函数,f2(.)代表了输出层的激励函数,通常使用S激励函数。
(2)数据与网络结构的设置
Elman神经网络模型利用均值回归模型求得profit,将profit数据的十个滞后量用来预测下一个profit值,当预期其将走低时,进行卖出profit操作,如果预测profit值将走高,那么进行买入profit操作。通过采用滚动分组的方式利用连续10个profit数据去预测第11个profit数据。首先笔者选取 2007 年 5月22日至 2013年11月29日的profit数据作为样本数据,其包含了19个合约共1589个数据。将前面18个合约共1509个数据作为样本区间内的训练数据,并依据此来建立套利策略。而最后的1401合约数据作为样本区间外的预测和模型评估。
对于任意的神经网络,如果隐藏层的节点数足够多,那么就可以无限的逼近一个非线性的函数。经过对不同隐藏层节点数的测试,笔者对于隐藏层节点的设置选择采用20。因此,在神经网络模型中,笔者选取隐藏层的层数为1层。网络的结构均采用 10-20-1 式,即含有10个输入节点、20隐藏层节点和1个输出节点的三层网络结构。输入层节点的输入为连续10日的实际profit 值,输出为第十一日profit的预测值。
(3)Elman神经网络开平仓信号
与均值回归模型中对与开平仓的设置类,具体的开平仓规则如下:
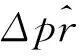
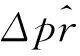
(4)样本区间内实证结果分析
基于前文提出的分析基础和策略上,分别在不同的阀值下,对样本区间内进行套利策略进行评价,结果如表3所示。
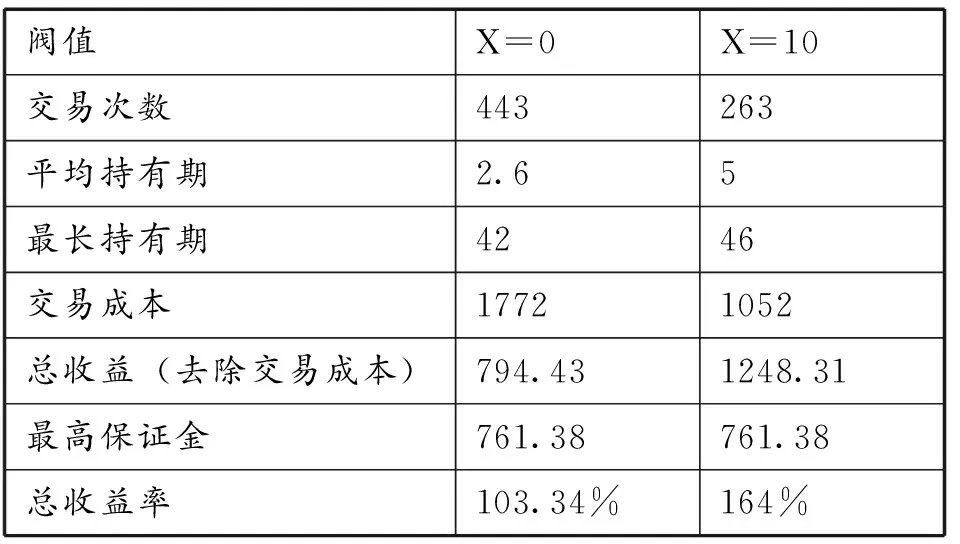
表3 基于Elman模型样本区间内套利交易情况
(5)样本区间外实证结果检验
前文根据Elman模型来构建1509个样本区间内数据的非线性关系,下面对2013年8月1日至2013年11月29日的80个数据进行样本区间外检验,结果如表4所示。

表4 基于Elman模型样本区间外套利交易情况
五、结论
选择大连商品交易所上市的豆一、豆粕和豆油期货进行跨商品套利研究,运用均值回归模型套利策略和Elman神经网络模型套利策略,通过设置不同的开平仓阀值,在样本区间内和样本区间外进行模拟实证。根据均值回归模型和神经网络模型进行套利模拟实证研究,从表1至表4的结果可以得出以下结论:
1、交易成本比较
传统的均值回归套利策略整体套利机会有限、交易成本低,样本区间内发生套利11次,样本区间外发生套利1次,累计交易成本仅为48元;而Elman神经网络套利策略整体套利机会频繁、交易成本高,样本区间内发生套利443次,样本区间外发生套利21次,交易成本累计高达1856元。
2、平均持有期比较
传统的均值回归套利策略头寸持有期较长,样本区间内头寸平均持有期为32.45个交易日,样本区间外头寸平均持有期为11个交易日;而Elman神经网络套利策略头寸持有期较短,样本区间内头寸平均持有期为2.6个交易日,样本区间外头寸平均持有期为3.3个交易日。
3、收益率比较
传统的均值回归套利策略收益率较低,样本区间内收益率为22.70%,样本区间外收益率为28.42%;而Elman神经网络套利策略收益率较高,样本区间内收益率为103.34%,样本区间外收益率为20.56%。随着开平仓阀值的不断提高,交易成本会不断减少,头寸持有期会延长,收益率会提高。当开平仓阀值为10时,样本区间内和样本区间外交易成本减少至1120元,样本区间内头寸平均持有期延长至5天,样本区间外头寸平均持有期延长至4.1天,样本区间内收益率提高至164%,样本区间外收益率提高至49.45%。因此,Elman神经网络套利策略在一定程度上要优于均值回归模型套利策略。
【参考文献】
[1]中研网. 2014年12月进口大豆853万吨全年7140万吨 [EB/OL]. http://www.chinairn.com/news/20150113/144733391.shtml, 2015-01-13.
[2]中国农业网. 期货市场在大豆产业中发挥怎样的作用? [EB/OL]. http://www.zgny.com.cn/ifm/consultation/2009-8-17/150022.shtml, 2009-08-17.
[3]Liu B J H, Wang Y B, Wang J J, Wu X, Zhang S. Is China the price taker in soybean futures? [J]. China Agricultural Economic Review, 2015, (3): 389-404.
[4]顾全,雷星晖. 基于协整的豆类期货统计套利实证研究[J]. 统计与决策,2015,(7):151-154.
[5]Simon D P. The Soybean Crush Spread: Empirical Evidence and Trading Strategies[J]. Journal of Futures Markets, 1999, (19): 271-89.
[6]Liu Q F W. Price relations among hog, corn, and soybean meal futures[J]. Journal of Futures Markets, 2005, (5): 491-514.
[7]Han L Y, Liang R, Tang K. Cross-market soybean futures price discovery: does the Dalian Commodity Exchange affect the Chicago Board of Trade?[J].Quantitative Finance,2013, (4): 613-626.
[8]杨升,何凌云,周曙东,张维娜. 大商所豆一与豆粕期货合约价格的协整性分析[J]. 中国管理科学,2008,(S1):302-305.
[9]Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, (5): 359-66.
[10]Dunis C L, Laws J, Evans B. Modelling and trading the soybean oil crush spread with recurrent and higher order networks: A comparative analysis[J]. Neural Network World, 2006, (3): 193-213.
[11]Wiles P S, Enke D. Nonlinear Modeling using Neural Networks for Trading the Soybean Complex[J]. Procedia Computer Science, 2014, (36): 234-239.
[12]王中香, 王凤, 何穗. 基于神经网络的黄金期货价格的预测[J]. 湖北师范学院学报(自然科学版),2009,(3):85-88.
[13]孙海涛,杨德平,李聪. 基于BP神经网络的我国股指期货价格预测[J]. 青岛大学学报(自然科学版),2012,(3):93-96.
[14]徐颢华,顾海峰. 股指期货短期价格预测模型研究——基于差分BP神经网络模型[J]. 金融教学与研究,2014,(3):27-32.
[15]Madhavan A, Smidt S. A Bayesian Model of Intraday Specialist Pricing[J]. Journal of Financial Economics, 1991,(1): 99-134.
(编辑:周亮;校对:余华)
Comparison Study on Soybean Futures Arbitrage Strategy Between Equilibrium Regression and Elman Neural Network
LIU Jian-he1LIANG Ren-fang1WANG Yu-bin2WU Wei3
(1.SchoolofFinance,ZhejiangUniversityofFinanceandEconomics,HangzhouZhejiang310018;2.SchoolofEconomicsandManagement,ChinaAgriculturalUniversity,Beijing100193;3.ResearchDepartment,Yong’anFuturesCompany,Ltd.,HangzhouZhejiang310005)
Abstract:This paper studies on the intra-commodity arbitrage of soybean futures and its squeezed soybean meal, soybean oil. In this paper, we use co-integration test and Error Correction Model to researd the relationship among the futures prices of soybean, soybean meal and soybean oil. By setting thresholds of opening and closing positions, this paper compares the arbitrage results of equilibrium regression method and those of Elman neural network method. The empirical results show that under the different thresholds of opening and closing positions, the Elman neural network method leads to better arbitrage results than equilibrium regression method.
Key words:soybean futures; arbitrage strategy; equilibrium regression method; Elman neural network method
DOI:10.16546/j.cnki.cn43-1510/f.2016.03.002
·收稿日期:2016-04-05
基金项目:浙江省科技厅软科学重点课题“关于浙江省引导私募基金投资促进经济转型升级对策研究”(项目编号:2015C25011)
作者简介:刘建和(1973-),男,浙江绍兴人,浙江财经大学金融学院教授,硕士研究生导师,研究方向:金融市场、家庭金融
【中图分类号】F323.7; F724.5
【文献标识码】A
【文章编号】2095-1361(2016)03-0013-08
