Signal Smoothing forAccurate Extraction of Low Signal-to-noise Ratio Cavity Ring-down Signal

HE Xing，LUAN Yinsen，DONG Lizhi，YANG Ping，XU Bing，TANG Guomao

(1.Institute of Optics and Electronics,Chinese Academy of Sciences,Chengdu610209,China;2.Key Laboratory on Adaptive Optics,Chinese Academy of Sciences,Chengdu610209,China;3.University of Chinese Academy of Sciences,Beijing100049,China)

Signal Smoothing forAccurate Extraction of Low Signal-to-noise Ratio Cavity Ring-down Signal

HE Xing1,2,3，LUAN Yinsen1,2,3，DONG Lizhi1,2，YANG Ping1,2，XU Bing1,2，TANG Guomao1,2

(1.Institute of Optics and Electronics,Chinese Academy of Sciences,Chengdu610209,China;2.Key Laboratory on Adaptive Optics,Chinese Academy of Sciences,Chengdu610209,China;3.University of Chinese Academy of Sciences,Beijing100049,China)

In cavity ring-down technique,a signal smoothing method based on spatial filters which have been used in digital image processing is presented for accurate cavity decay time extraction of low signal-to-noise ratio decay signal. Its smoothing procedure was derived and its smoothing efficiency was compared with other smoothing methods. Derivation showed the mean value spatial filter had the highest smoothing efficiency.The application of decay signal smoothing was also analyzed.The combination of the mean value spatial filter with the weighted least square methods was recommended when processing low signal-to-noise ratio decay signals.This method was tested in experiment and achieved almost the same results with the Levenberg-Marquardt algorithm.

cavity ring-down;decay time extraction;signal smoothing

0 Introduction

The cavity ring-down(CRD)technique has been successfully used for measurement of absorption[1]and high reflectivity[2].In this technique,a ring-down cavity(RDC),one kind of passive resonator,is built first.Then a laser pulse or continuous wave controlled by optical switch element is injected,meanwhile the transmission signal behind certain cavity mirror is recorded.For there are intracavity optical losses,the transmission signal will decayexponentially after the laser pulse is injected or the continuous wave is switched off[1].The elapsed time to 1/edecay is defined as the cavity decay time,which is a measure of cavity total loss.

Cavity total loss includes intracavity absorption,cavity mirror transmission,and diffraction,etc[2].To obtain the absorption loss or mirror reflectivity,a comparison procedure is inevitable.Take the measurement of weak absorption as an example,the total loss of RDC without detected gaseous material,the so-called empty RDC,is measured first,then the detected gaseous material is put in and the total loss of this RDC,the so-called test RDC, is measured again.In this way,the absorption of detected gaseous material,which causes the variation of RDC total loss,can be calculated.It is essential to ensure the measurement accuracy and precision of RDC loss in this procedure,therefore the accurate extraction of cavity decay time from noisy decay signal is significant.

A number of extraction methods have been adopted in cavity decay time extraction,such as the nonlinear least square fitting(NLSF)algorithms[3-5],the weighted least square(WLS)methods[6-7],and the Fourier transform (FT)method[8-10],etc.The comparisons of them have been presented by Refs.[11-14].According to the derivations of He et al[7]and Lehmann et al[13],the extraction precision of an extraction method is inverse proportional to the signal-to-noise ratio(SNR)meanwhile the extraction bias,which is a measure of accuracy,is inverse proportional to the square of SNR.Here,SNR is defined as the ratio of signal amplitude to standard deviation value of noise.If SNR is high enough,these methods can achieve nearly the same accuracy and precision.However,if SNR decreases,these methods suffer degenerations to different degrees and the NLSF methods seem to be the most reliable one among them.Sometimes,the low amplitude decay signals,which will result in low SNR,are inevitable in CRD measurement.They may be caused by the occasional low coupling efficiency between laser source and the RDC,the finite gain of the photodetector(PD),or the relatively large loss brought by the measured object.Thus,those CRD systems such as real-time CRD that adopted these fast extraction methods such as FT method[15]are brought potential drawback.For example,if the loss brought by the measured object is large enough, the measurement accuracy of the empty RDC and the test RDC will be different.If the extraction performance of these fast methods can be improved under condition of low SNR signals,the reliability of these CRD systems can be enhanced.To solve this problem,we can try to smooth the decay signal to achieve a defacto higher SNR.The smooth procedure should be as fast as possible.There have been several smoothing methods such as the mean displaced ratio(MDR)method developed by Dyson and Isenberg[16]and the method suggested by Provencher[17]. We find both of them take a very large computation cost which is the total amount of float point calculations in signal decay signal processing.So we try to utilize another kind of signal smoothing method which is similar with spatial filtering in digital image processing(DIP)technique.

In this paper,spatial filtering and other two methods for low SNR decay signal smoothing are analyzed and compared.By deriving their smoothing efficiency,we find that the mean value spatial filter is very proper for low SNR decay signal analysis.With spatial filtering,we further compared the extraction performance and computation cost of the WLS methods and the NLSF algorithms comprehensively,and give a guideline of method choosing under certain condition.According to these derivations,the combination of the WLS-DS method[8]and mean value spatial filter is recommended for low SNR decay signal analysis.This method was tested in an optical feedback CRD(OF-CRD)setup.

1 Theory

The spatial filtering in DIP technique actually corresponds to the weighted averaging of certain pixel’s neighborhood[18].The weight values constitute the filter kernel which is a matrix in DIP.For some spatial filters such as the median value filter and the maximum filter,their weight values can be regarded as specially determined to make only certain pixel to be selected out.The smoothing of decay signal can be executed in asimilar way with a vector filter kernel.

1.1 Derivations of the Smoothing Efficiency of the Spatial Filters

Before the analyses and comparisons of spatial filters,we first write the decay signal as a serial,that is,

Here:Iis decay signal,τis cavity decay time,Ois instrumental offset,andεis background noise.The relationτbetween and cavity loss can be given by

Here:δis cavity loss,cis light speed,andlis cavity length.We can see thatδis proportional to 1/τ,so its precision and accuracy can be analyzed in the same way as 1/τ.

For a given normalized filter kernelfwith nonnegative weight values[f-L,…,f0,…,fL]in it,whereLis a measure of the filter kernel length.The filtering result of thejthdata point,written asYj,is

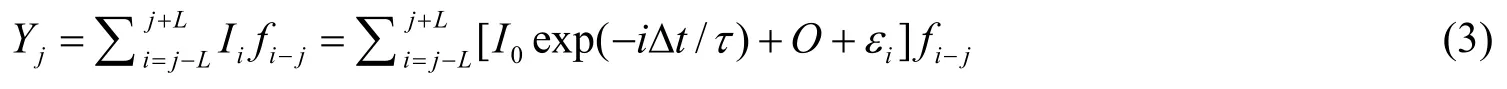
Here:j=0,…,N-1;Nis the number of data points,Δtis the time interval of data acquisition,Derive the terms in the right side one by one,we can get:

Unlike the smoothing methods presented by Ref.[16]and Ref.[17],the smoothing based on spatial filter has no sensitivity toO.On the other hand,if we assume thatεis normally distributed with standard deviation value ofes,the last term of Eq.(4)is also normally distributed but with standard deviation value of:

Herefsis the standard deviation value of the filtered noise serial.The last equal sign is tenable only if certainfi=1.

We rearrange the first term of the right side of Eq.(4)as:

We can find that the amplitude of decay signal after spatial filtering will be multiplied a constant factor, which noted asAfor concision in description,that is,

Ahas no dependence onj,so it just gives the decay signal a proportional ratio.Note that Δt/τshould be far less than one as indicated by Ref.[13],andLis not expected to be very large,soAis quite closed to 1.

Then,the smoothing efficiency,which contains the constraining ability of noise’s standard deviation value and the computation cost,can also be calculated.The constraining ability of noise’s standard deviation value is given by Eq.(5),and the computation cost is(2·L+1)times multiplications and 2·Ltimes additions for each data point.For some special filter kernels,the computation cost can be lower.

For comparison,the smoothing efficiencies of the MDR method and the method in Ref.[17]are also derived here.The MDR method can be equally described:

Here:L1is the number of the data points for smoothing calculation.The method presented by Ref.[17]is shown as:

Here,L2is also the number of the data points for smoothing calculation.

We can compare the smoothing efficiency of these methods in Fig.1.From Eq.(9)we can know that the mean value spatial filter,whose weight values are all 1/(2·L+1),has the highest smoothing ability for a givenL,so we choose the mean value spatial filter in this comparison.

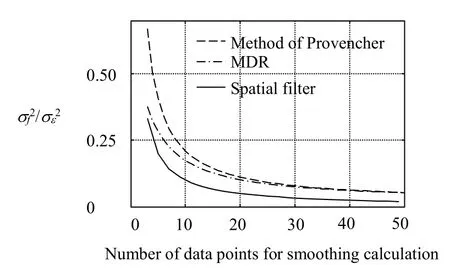
Fig.1(Color online)Comparison of smoothing efficiency of these methods

It should be noticed that for the spatial filter,the first green square means the corresponding filter lengthLis 1(number of data points for filtering is 3),the second one meansLis 2(number of data points for filtering is 5), and the like.Besides,the smoothing efficiency of MDR or the method in Ref.[17]has a dependence onjwhich is set to 1 here.We can see that the spatial filter has the highest smoothing efficiency among these methods,which means it will take the lowest computation cost to achieve certain smoothing level.

1.2 TheApplications of the Spatial Filters

In actual application,we found several noticeable details which make us analyzed the spatial filters further to find some guidelines to their utilizations.

At first we noticed that the improvement on cavity decay time extraction was not as large as the theory indicates(we choose the theoretical derivations by Lehmann[13]as the theory guideline).Taking the following simulation as an example,whereI0=0.2,σε=0.01(the SNR was 20),τ=1.2 μs,O=0.02,Δt=12.5 ns,andN= 5000.We used the NLSF algorithm and the WLS-DS method(withk=0.03 andb=1´10-4)to fit the cavity decay time.For the SNR was relatively low,we applied the mean value spatial filters withL=5 to smooth the decay signals.The statistical results of ten thousand simulated decay signals were presented in Table 1.

Table 1The comparison of extraction performance whenL=5

The mean value spatial filter withL=5 can decreaseto the one-eleventh of itself,so the accuracy should be improved by 11 times meanwhile the precision will improve about 3 times[7,13].We could see that improvement on accuracy was basically as expected;however,the precision had almost no change.However,if we changedσεto be 0.003 3,the result of the WLS-DS method would be(1.193±0.007)μs without spatial filtering.Based on these results,we could conclude that the derivations in Refs.[7,13]are correct;however,the extraction precision cannot be improved as expected.We attribute this problem to the correlation of the noise after spatial filtering.

After spatial filtering,one data point will correlate with 2·Lneighboring data points,i.e.,only two data points with an interval of at least(2·L+1)are statistically independent.One may think that the precision can be improved by just fitting the data points with interval of(2·L+1).In fact,it is an illusion because the change of data point interval corresponds to the change ofΔt,and the precisions of the WLS-DS method and the FT methods depend onΔt[7,13],too.If we choose the data points with interval of(2·L+1)for extraction,the data acquisition interval will be(2·L+1)·Δtmeanwhile the lowestσfis only(2·L+1)-1/2·σε.For the WLS-DS method,its extraction precision is proportional to[7],which means we can only achieve the same precision in this way.For the FT method whose precision is proportional toDt×es[13],the precision even degenerates after this processing.

Therefore,a conclusion can be made that the spatial filter has no improvement on extraction precision of neither the WLS-DS method nor the FT methods.However,with the help of spatial filter the WLS-DS method can achieve nearly the same precision and comparable accuracy with the NLSF algorithms.The comprehensive comparisons of the NLSF algorithms and the WLS-DS method with spatial filter are given in Table 2,where the computation cost is essential for these methods.If those methods with spatial filters are slower than the NLSF algorithms,there is no need to apply the spatial filters at all.Here,the derivation results are all based on 1/τ.

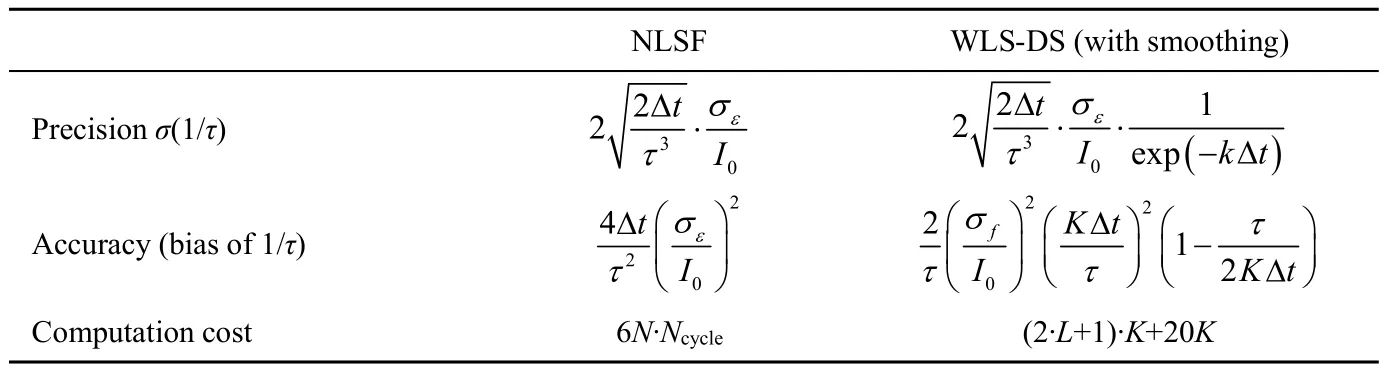
Table 2The comprehensive comparisons of the NLSF and the WLS-DS methods

There are several details should be supplemented for Table 2.The first one is that in the column of NLSF,the derivations of precision and accuracy are cited from Ref.[13].Ncyclemeans the number of iterations of the NLSF methods.In this simulation the iterations stopped whenNcycle=2,but we found that the fitting results ofNcycle=1 andNcycle=2 were quite close,so we thoughtNcycle=1 is enough in fact.Besides,6Ncalculation per iteration cycle is the fastest speed of the NLSF methods[13].In the column of WLS-DS,the expression of precision and accuracy are cited from Ref.[7]and Ref.[13].Kis the number of data points for fitting which is equal toNfor the common WLS method,but is less thanNfor the WLS-DS method(for example,Kin the former simulation was about 550, just 0.11N).In addition,if we adopt mean value spatial filter,the multiplication ofIi·fican be saved so the computation cost will be 2Ladditions and one division.

We also consider the effect of spatial filtering on data processing bandwidth.In the column of WLS-DS,we can find the fitting performances are related to ΔtandσfHere,Δtis related to bandwidth andσfis related to spatial filtering.These two parameters are independent from each other,so spatial filtering has effect on data processing bandwidth.

Based on Table 1 and Eq.(6),we can choose the more proper method by comparing their extraction performances and computation cost together.Taking the former simulation as an example,the WLS-DS method could achieve nearly the same precision with the NLSF algorithm and fine accuracy after spatial filtering withL=5. Under this condition its computation cost was about 3.4Nwhich was lower than an iteration cycle of the NLSF method.Even we setLto nine,its computation was only about 4.3N.Therefore,we recommend the combination of the WLS-DS method and the mean value spatial filter to extract cavity decay time in low SNR cases.

2 Experiment

An OF-CRD setup was constructed as Fig.2 to test the effect of spatial filter in low SNR cases.In Fig.2,the solid line corresponds to the light path,and the dot line corresponds to the signal path.The V-shaped RDC is denoted by the bold solid lines.

The laser source is a CW F-P laser(Power Technologies,IQ1A07,1 060 nm).A square wave generator(Spectrum,M2i.6021)is used as the optical switch element whose modulation frequency is 100 Hz.A variable attenuator noted asAis adopted to vary the intensity of retro-reflected light from RDC.The V-shaped RDC is constructed by two plano-concave mirrors(M1,M2)and one plane mirror(M3).All of the cavity mirrors are coated with high reflectivity films.The curvature radiuses ofM1andM2are both 1 m.The transmission light of RDC is focused on photodetector(PD,Thorlabs,PDA400)by the lensL1.Then the data is acquired from PD by a data acquisition(DAQ)card(Spectrum,M2i.3010,80 MHz).The attenuator,lensL1,and the PD are all slightly tilted to avoid the retro-reflected light because the feedback light may affect the spectral characteristics of the semiconductor laser source[19-20].Here,a He-Ne laser and two plane mirrors are adopted to align this setup.

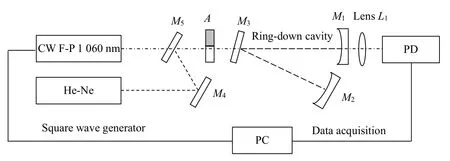
Fig.2(Color online)Schematic diagram of our experimental OF-CRD setup

A groups of decay signals with SNR was about 42 was analyzed.There were 80 decay signals which contained 4 000 data points each.In this experimentsεwas 0.004 V andτwas about 2.2 μs.We first compared the WLS-DS method with NLSF algorithm by simulation under this SNR condition.They both need an initial guess value ofτ,which we set to 2.2 μs here.Fitting results were(2.172±0.011)μs for the WLS-DS method(withk=0.03 andb=1·10-4)and(2.200±0.011)μs for NLSF algorithm.There would be 1.27%bias for the WLS-DS method.We used the mean value spatial filter withL=2～6 to smooth the decay signals in turn.The data processing results were shown in Table 3 and Fig.3.

Table 3The fitting results of the experimental decay signalsμs

Fig.3(Color online)Fitting results of experimental decay signals

The fitting result of NLSF algorithm was(2.240±0.066)μs,the result of the WLS-DS method with spatial filter(L=3)was(2.240±0.068)μs,while the result of the WLS-DS method along was(2.207±0.069)μs(1.47% bias compared to the NLSF algorithm).When filter length was 2,the result was(2.239±0.068)μs,whereas the spatial filter with length of 4～6 all given the result of(2.241±0.068)μs.We can see the improvement on fitting accuracy was just as expected.There were two possibly reasonable results that were 2.240 μs and 2.241 μs.Nomatter which result was chosen as the standard,all the relative biases were decreased from 1.47%to less than 0.1%after mean value spatial filtering.Meanwhile the precision was same to the NLSF algorithm.

Then we analyzed the computation cost of these methods.We noticed that the iteration of NLSF algorithm stopped after 3 cycles,but actually 2 cycles were enough.This result was one more cycle than the simulation case in former section,which may because the considerable initial guess error ofτ(2.2 μs to 2.24 μs).With such an initial guess error,we can see the fitting result of the WLS-DS method was still reliable.Another detail was that mean value ofKwas 689.3 andNwas 4 000 in this experiment.Ref.[7]had indicated that float point calculations of WLS-DS method is no more than 20K,so the computation costs were 20·689.3=13 786 for the WLS-DS method and 4 000´6´2=48 000 for the NLSF algorithm.The computation cost of the WLS-DS method was much lower than the NLSF algorithm.

Then,we tested this smoothing method again by analyzing two groups of decay signals with different SNRs. In this experimentτwas about 1.5 μs.We used mean value spatial filter withL=3 to preprocess the decay signals. The results were shown in Table 4.

We could conclude from this table that the smoothing of mean value spatial filter is quite helpful for fast and accurate processing of low SNR decay signals.

Table 4The fitting results of the experimental decay signalsμs

3 Conclusion

This paper presents a cavity decay time extraction method,which combines the WLS-DS method with spatial filters,for fast and accurate analysis of low SNR decay signal.At first,the smoothing procedure of spatial filter is derived in detail and compared with other methods.In this way,we found that the mean value spatial filter has the highest smoothing efficiency.Then,we found the extraction accuracy was obviously improved after spatial filtering;however,the extraction precision just improved a little because for the correlation between neighboring noise points brought by the spatial filtering.This meant that the WLS-DS method,combined with spatial filters, can achieve nearly the same result with the NLSF methods at most.Now that the extraction performances are almost definite under certain condition,the computation cost was taken into consideration.After derivation and comparison,we believe the mean value spatial filter together with the WLS-DS method can be a fine extraction method when coping with low SNR decay signals.

For the spatial filter do not affect the exponential nature of decay signal,it can be used to the exponential analysis field which contains multi-exponential decays,too.

[1]O’Keefe A，Deacon D A G.Cavity ringdown optical spectrometer for absorption measurements using pulsed laser sources[J]. Review of Scientific Instruments(S1089-7623)，1988，59：2544-2551.

[2]Anderson D Z，Frisch J C，Masser C S.Mirror reflectometer based on optical cavity decay time[J].Applied Optics (S1559-128X)，1984，23(8)：1238-1245.

[3]Naus H，Stokkum I H M van，Hogervorst W，et al.Quantitative analysis of decay transients applied to a multimode pulsed cavity ringdown experiment[J].Applied Optics(S1559-128X)，2001，40：4416-4426.

[4]Lerber T von，Sigrist M W.Time constant extraction from noisy cavity ring-down signals[J].Chemical Physics Letter(S0009-2614)，2002，353：131-137.

[5]HUANG H F，Lehmann Kevin K.Sensitive limit of rapidly swept continuous wave cavity ring-down spectroscopy[J].TheJournal of Physical ChemistryA(S1089-5639)，2011，115：9411-9421.

[6]Romanini D，Lehmann K K.Ring-down cavity absorption spectroscopy of the very weak HCN overtone bands with six，seven，and eight stretching quanta[J].The Journal of Chemical Physics(S0021-9606)，1993，99：6287-6301.

[7]HE Xing，YAN Hu，DONG Lizhi，et al.Data point selection for weighted least square fitting of cavity decay time constant[J]. Chinese Physics B(S1674-1056)，2016，25(1)：014211.

[8]Mazurenka M，Wada R，Shillings A J L，et al.Fast Fourier transform analysis in cavity ring-down spectroscopy：application to an optical detector for atmospheric NO2[J].Applied Physics B(S0946-2171)，2005，81：135-141.

[9]Everest M A，Atkinson D B.Discrete sums for the rapid determination of exponential decay constants[J].Review of Scientific Instruments(S1089-7623)，2008，79：023108-1.

[10]Boyson T K，Spence T G，Calzada M F，et al.Frequency domain analysis for laser-locked cavity ringdown spectroscopy[J]. Optics Express(S1094-4087)，2011，19(9)：8092-8101.

[11]Istratov AA，Vyvenko O F.Exponential analysis in physical phenomena[J].Review of Scientific Instruments(S1089-7623)，1999，70：1233-1257.

[12]Fuhrmann N，Brühach J，Dreizler A.On the mono-exponential fitting of phosphorescence decays[J].Applied Physics B (S0946-2171)，2014，116：359-369.

[13]Lehmann Kevin K，HUANG Haifeng.Optimal signal processing in cavity ring-down spectroscopy[M].Elvevier，2009：623-658.

[14]王丹，胡仁志，谢品华，等.腔衰荡光谱技术中衰荡时间的准确快速提取[J].光谱学与光谱分析，2014，34(10)：2845-2850. WANG Dan，HU Renzhi，XIE Pinghua，et al.Fast and accurate extraction of ring-down time in cavity ring-down spectroscopy [J].Spectroscopy and SpectralAnalysis，2014，34(10)：2845-2850.

[15]Spence T G，Calzada M E，Gardner H M，et al.Real-time FPGA data collection of pulsed laser cavity ringdown signals[J]. Optics Express(S1094-4087)，2012，20(8)：8804-8814.

[16]Dyson R D，Isenberg I.Analysis of exponential curves by a method of moments，with special attention to sedimentation equilibrium and fluorescence decay[J].Biochemistry(S0006-2960)，1971，10：3233-3241.

[17]Provencher S W.An eigenfunction expansion method for the analysis of exponential decay curves[J].The Journal of Chemical Physics(S0021-9606)，1976，64：2772-2777.

[18]Gonzalez R C，Woods R E.Digital Image Processing：Third Edition[M].Beijing：Publishing House of Electronics Industry，2010：167-168.

[19]Morville J，Romanini D.Sensitive birefringence measurement in a high-finesse resonator using diode laser optical self-locking [J].Applied Physics B(S0946-2171)，2002，74：495-509.

[22]GONG Yuan，LI Bincheng，HAN Yanling.Optical feedback cavity ring-down technique for accurate measurement of ultra-high reflectivity[J].Applied Physics B(S0946-2171)，2008，93：355-360.

1003-501X(2016)11-0046-08

精确提取低信噪比光腔衰荡信号的信号平滑

何 星1,2,3，栾银森1,2,3，董理治1,2，杨 平1,2，许 冰1,2，汤国茂1,2
(1.中国科学院光电技术研究所，成都610209；2.中国科学院自适应光学国家重点实验室，成都610209；3.中国科学院大学，北京100049)

提出一种用于低信噪比光腔衰荡时间准确提取的信号平滑方法，该方法基于数字图像处理领域的空间滤波平滑技术。首先推导了这种平滑方法的平滑过程和平滑效率，并与其他平滑算法进行了对比。推导结果表明基于均值滤波算子的空间滤波平滑方法具有最高的平滑效率。其次，分析了信号平滑方法的实用效果，结果发现该平滑方法与加权线性最小二乘算法相结合能够实现高精度、快速同时准确度较好的光腔衰荡时间提取。最后结合实验数据检验了平滑方法的处理效果，取得了列文伯格-马夸尔特算法相一致的衰荡时间提取结果。

光腔衰荡技术；衰荡时间提取；信号平滑

2016-03-14；

2016-04-26

四川省杰出青年基金资助项目(2012JQ0012);国家重点科研装备开发项目资助(ZDYZ2013-2)

何星(1989-)，男(汉族)，河北石家庄人。博士研究生，主要研究工作是光学检测。E-mail:hexingjiayou@126.com。

许冰(1960-)，男(汉族)，浙江天台人。研究员，主要研究工作是自适应光学技术。E-mail:bing_xu_ioe@163.com。

TP391

A

10.3969/j.issn.1003-501X.2016.11.008