求解声波动方程的隐格式有限体积法

宣领宽, 龚京风, 张文平, 袁兴军

(1.中国舰船研究设计中心, 武汉 430064; 2.哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001)

求解声波动方程的隐格式有限体积法

宣领宽1, 龚京风1, 张文平2, 袁兴军1

(1.中国舰船研究设计中心, 武汉 430064; 2.哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001)

摘要:为研究声传播问题,提出一种声波动方程的隐格式有限体积法,该方法将格点型有限体积法与Newmark格式相结合．模拟平面波的传播过程,对比分析隐格式有限体积法和文献中显格式有限体积法的精度、稳定性及计算消耗等方面的性能．数值结果表明:当λ/Δx≥10时,两种算法均能得到满足精度要求的解;采用无条件稳定的隐格式算法,当满足ω0Δt≤0.3时,预测声压的相对峰值误差<1%;当采用相同时间、空间步长时,隐格式算法精度高于显格式算法;隐格式算法对吸收边界的处理精度高于显格式算法,但对全反射边界的处理精度低于显格式算法;两种算法内存消耗比较接近,显格式算法的CPU耗时较少．

关键词:有限体积法;差分格式;Newmark格式;声波动方程;平面波

近年来,有限体积法(FVM)被逐渐应用于声学问题,其目的是采用统一方法求解多物理场(如流固声耦合)问题,避免混合方法带来的一系列问题(如收敛困难)[1]．Fogarty等[2]尝试将FVM应用于一维、二维周期性材料及随机材料等属性变化剧烈介质中的声传播问题．Del-Pino等[3]利用高阶Lax-Wendroff格式提出高阶FVM,并应用于模拟地球大气中的大尺度声传播问题．宁立方等[4]采用FVM求解流体Navier-Stokes方程,模拟一维谐振管内的非线性驻波．宣领宽等[5]基于非结构四面体网格将FVM应用于求解三维非均匀介质声波动方程,并基于时域脉冲法将其扩展应用于预测消声器的传递损失．目前,基于FVM求解声波动方程的算法主要采用显格式算法[2-5]．显格式算法形成的矩阵通常非常稀疏,甚至不需要采用矩阵形式即可求解,其对存储的消耗很低;同时,不需要特定的线性方程组求解器,算法的程序实现比较容易,且计算效率高. 刘恒等[6]指出提高计算效率的重要途径是发展显格式算法;但是,由于稳定性条件的限制,显格式算法需要的时间步长会随着网格的加密而减小,此时会造成显格式算法的计算效率大大降低．隐格式算法的无条件稳定却有可能解决这一问题．

针对声波动方程,本文采用格点型FVM离散其空间项,Newmark格式离散其时间项,算法上采用隐格式算法．模拟平面波的传播,对比分析本文隐格式Newmark算法与文献中显格式中心差分算法的精度、计算消耗、稳定性及边界条件处理正确性．

1基本方程

静态非均匀流体中的声波动方程为

(1)

文中涉及两大类边界条件:(a)全反射边界条件[7],包含“绝对硬”理想边界Γv与“绝对软”理想边界Γp,可分别表示为p·n=0与p=0;(b)一阶吸收边界条件Γb做为对无穷远的近似,表示为[8]

2数值离散

本文采用隐格式法求解声波动方程,并与文献[9]的显格式法对比．二者共同点是声波动方程中的空间项都是基于格点型FVM离散,区别在于显格式法中时间项采用中心差分格式离散,显式推进求解离散方程,而隐格式法中时间项采用Newmark格式离散,隐式迭代求解离散方程．式(1)的积分形式为

(2)

格点型FVM在离散过程中会用到单元的型函数,常见的网格单元形式有三角形、四边形、四面体、三棱柱、六面体[10]．本文以二维四边形单元为例．

2.1空间离散

图1为二维声场控制体积示意图,计算域用4节点四边形单元划分．在内部节点a周围建立边界Γint为3-4-5-6-7-8-9-10-3的控制体Ωa,在边界节点b周围建立边界Γint为1-5-4-3-2-b-1的控制体Ωb．密度ρ、声速c定义在单元中心,并假设其在单元内均匀分布;待解变量声压p定义在节点上,并假设在控制体内均匀分布．参考文献[11],假设声压加速度在内部控制体Ωa内均匀分布,式(2)的左端表示为

(3)

式中:na为节点a周围单元总数,ρi、ci为节点a周围第i个单元内的密度、声速,(Sa)i为节点a周围第i个单元中参与控制体内的面积,ga为节点a集中属性．

式(2)的右端项采用高斯定理

∫Ω·(ρ-1p)dΩ=∫Γintρ-1p·ndΓ=

(4)

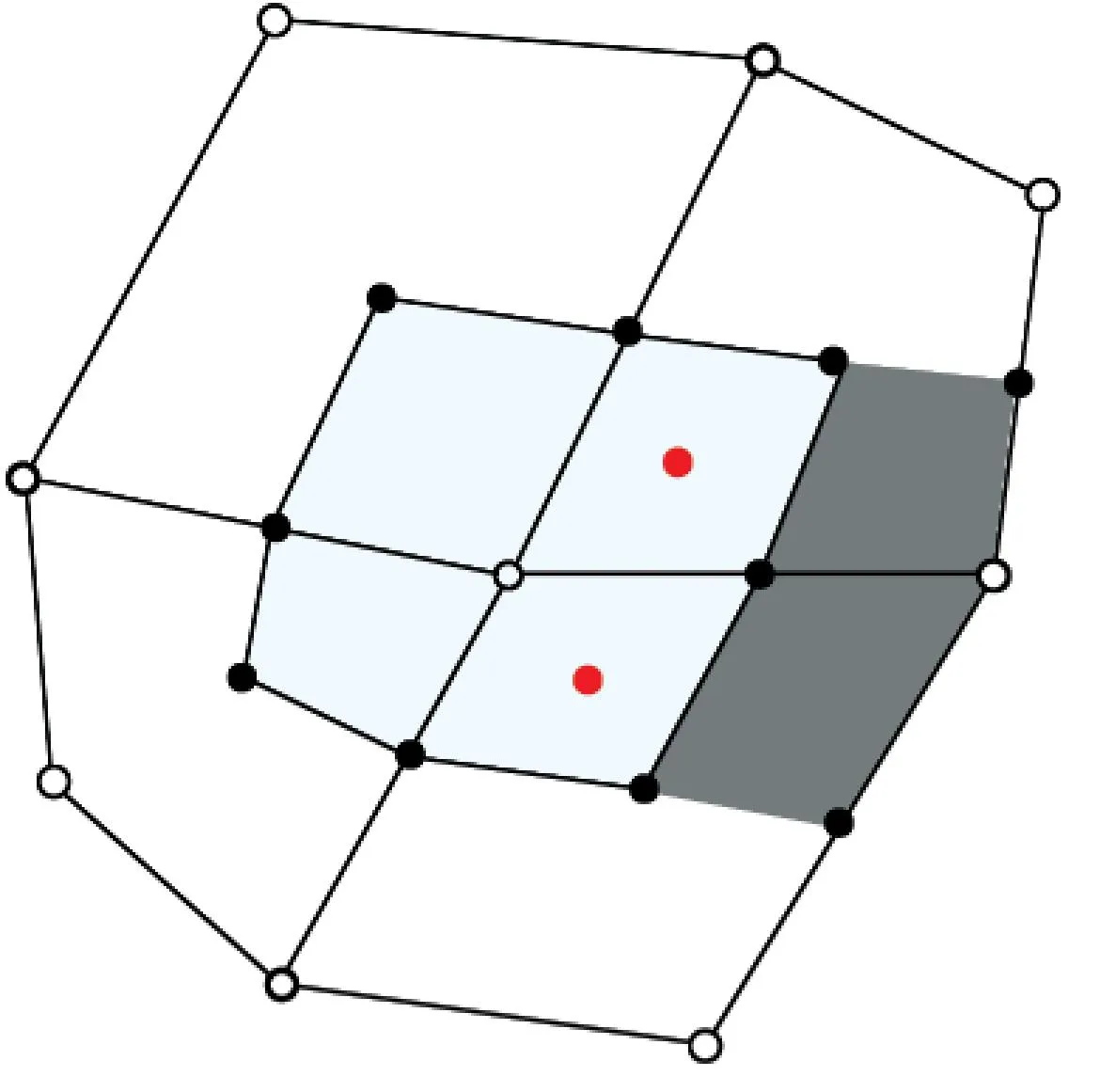
图1　二维声场控制体积示意

引入型函数,单元内的压力梯度为

式中:N为型函数, ∂Nj/∂x、∂Nj/∂y的表达式可参考文献[9-12]．

由式(3)、(4),式(2)可变为

(5)

式中:下标ij表示节点a周围第i个单元内第j个节点,四边形单元中kij的表达式见2.2节．

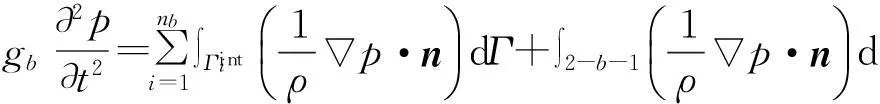
(6)

假设为“绝对硬”全反射边界条件,则式(6)右端第二项为零,自然满足．

假设为吸收边界条件Γb,则式(6)右端第二项可表示为

(7)

式中:L2-b、Lb-1分别为边2-b、b-1的长度,(ρc)3、(ρc)5分别为单元abcd、abef内的密度、声速的乘积．

由式(6)、(7),式(5)可变为

式中,nbn为节点b周围的节点总数(包含节点b), 则

(8)

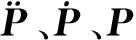
2.2四边形单元处理

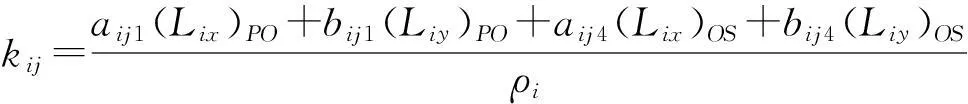
式中,ρi为节点1周围第i个四边形单元C1234的密度,且有

式中(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)分别为四边形单元节点1、2、3、4的坐标．

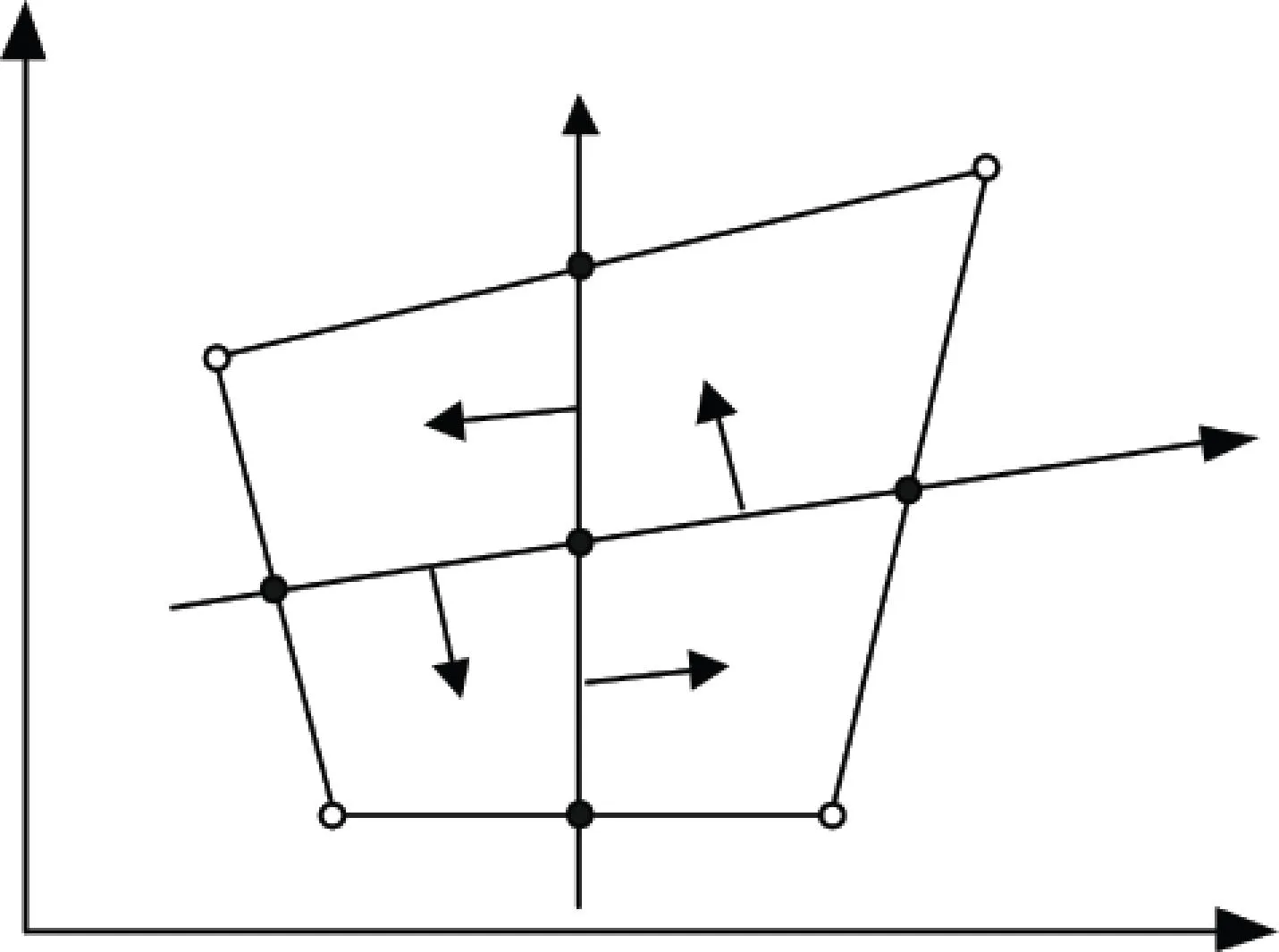
(a)整体坐标系

(b)局部坐标系

2.3时间离散

二阶时间项的离散可采用的隐格式算法有线性加速度法、Newmark法及Houbolt法等. 文献[13]指出,线性加速度法可选择的时间步长较小,而Newmark法的计算精度比Houbolt法高．同时,Newmark法是结构动力学中最流行的一种方法,文献[11]指出,当δ≥0.5,α≥0.25(0.5+δ)2时,Newmark法是无条件稳定的．文献[14]指出当ω0Δt<0.3时(ω0为固有频率对应的角频率),数值阻尼<2%,系统固有频率误差<1%．因此本文尝试采用Newmark法求解二阶时间项,并与格点型FVM相结合,将Newmark法用于求解式(8)(K-1/(αΔt2)G-δ/(αΔt)C)Pt+Δt=

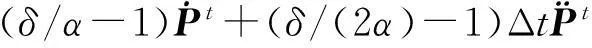
(9)

依据式(9)可获得节点声压p,节点声压速度、加速度可分别由式(10)、(11)更新:

(10)

(11)

由式(10)、(11),式(8)可变为以节点声压P为未知量的线性系统,可采用迭代求解器或直接求解器进行求解,本文采用迭代求解器代数多重网格法[15]求解．“绝对软”全反射边界条件,可采用置大数法或置“1”法等[16]进行处理．

3两种格式比较

为方便对比两种格式,研究图3所示的声学计算域,上下为绝对硬边界Γv,左侧施加高斯压力脉冲

其中:T′=2.5×10-3s,声速c=500m/s,密度ρ=1kg/m3．

图3　矩形声场计算域

3.1空间步长的影响

表1中4种均匀分布的四边形单元用于网格无关性分析,时间步长均为Δt=5×10-5s．监测点M声压的时域响应如图4所示,Grid2、Grid3及Grid4的结果相互吻合良好,所以当λ/Δx≥10,显格式法与隐格式法均能够获得满足精度要求的解,Grid3能够用于进一步分析．表1中给出两种格式的内存和CPU消耗,二者的内存消耗区别不大,但时间步长Δt相同时,显格式消费的CPU时间更少．

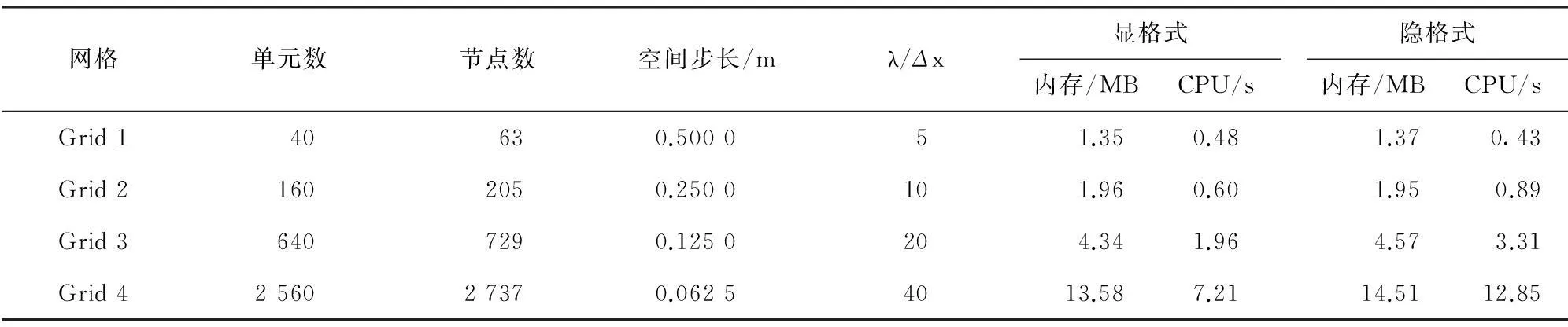
表1　计算详细信息

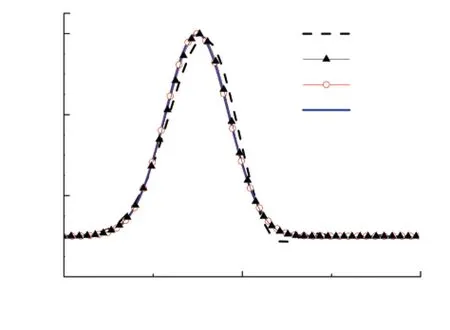
(a)显格式

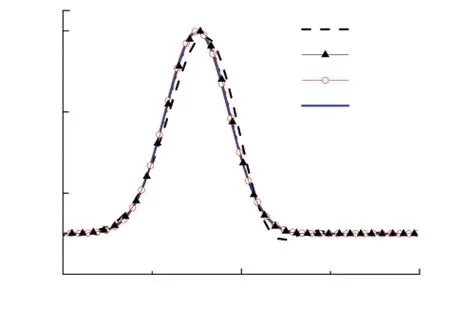
(b)隐格式

3.2时间步长的影响

利用Grid 3分析时间步长对计算结果的影响．表2中列出两种格式点M声压的峰值误差．针对显格式算法,(c0Δt)/dx=0.98、1.00时,计算结果稳定且吻合良好;当(c0Δt)/dx=1.02>1.00时,计算结果发散,说明显格式算法是条件稳定的,且稳定性条件与文献[10]的推导结果基本一致．针对隐格式算法,ω0Δt=0.1、0.3时,计算结果吻合良好,但ω0Δt=0.50、0.51及0.60时出现明显衰减,其中ω0=2πf ′max,5种情况下的结果均没有出现发散,表明隐格式算法是无条件稳定的．当ω0Δt=0.3时,相对误差<1%,对应一个周期内21个时间采样点,小于文献[17]中33个时间采样点．当ω0Δt> 0.5时,预测声压级差超过工程上±0.5dB的误差需求,一个周期内有13个时间采样点．相对误差、绝对误差、声压级差分别由式(12)～(14)计算:

相对误差=(p预测-p解析)/p解析×100%,

(12)

绝对误差=|p预测-p解析|,

(13)

声压级差=20×lg10(p预测/p解析).

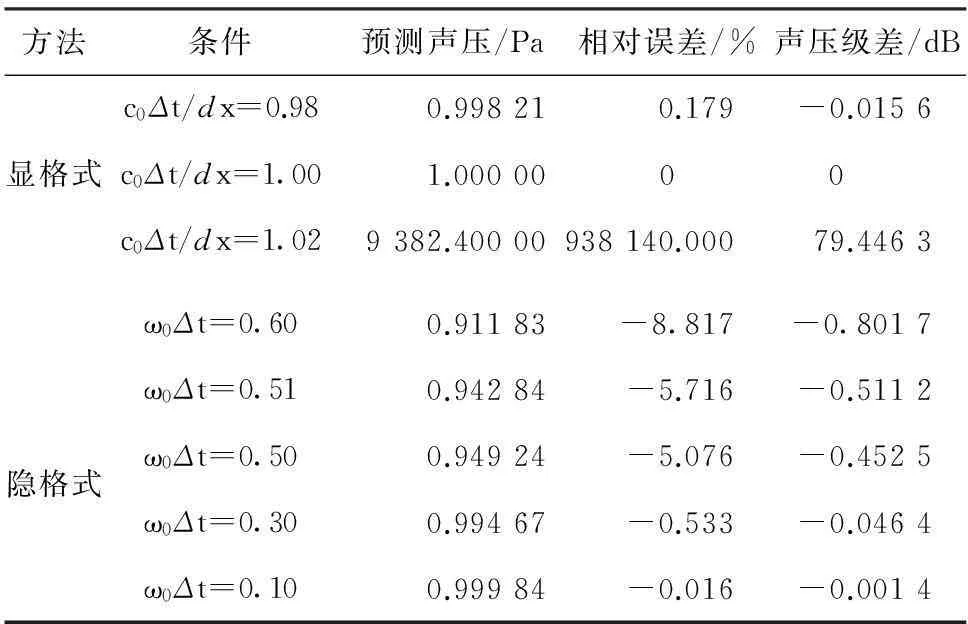
(14)

基于Grid3,采用3种时间步长,对比隐格式和显格式方法得到点M声压的绝对误差,见图5．结果表明,基于相同的计算网格和时间步长,隐格式方法得到的结果与精确解吻合更好．

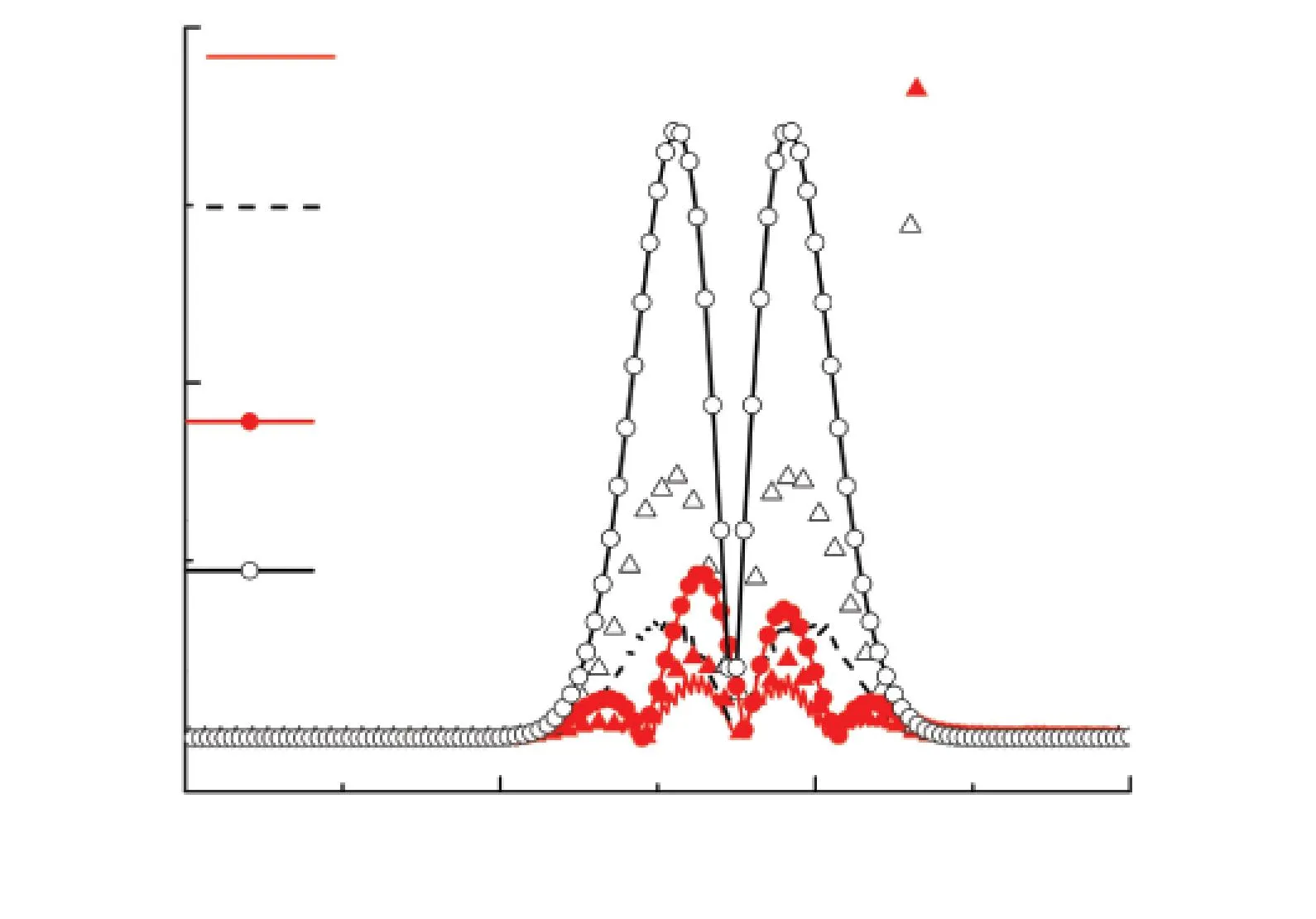
图5　不同时间步长时两种格式绝对误差的比较

3.3边界条件的影响

分析两种方法处理绝对软边界、绝对硬边界、吸收边界的正确性,基于Grid3,时间步长Δt=1.25×10-4s,右侧边界分别为不同边界条件时点M声压(见图6)．当右侧边界为绝对软边界时,两种格式均存在反相同幅值反射;当右侧边界为绝对硬边界时,两种格式均存在同相同幅值反射;当右侧边界为吸收边界时,均将波成功透射出去．

图7为不同边界条件下点M声压的绝对误差,隐格式算法得到的入射波精度高于显格式算法;对全反射边界条件的处理,显格式算法的精度高于隐格式算法;对吸收边界条件的处理,显格式算法的精度低于隐格式算法．

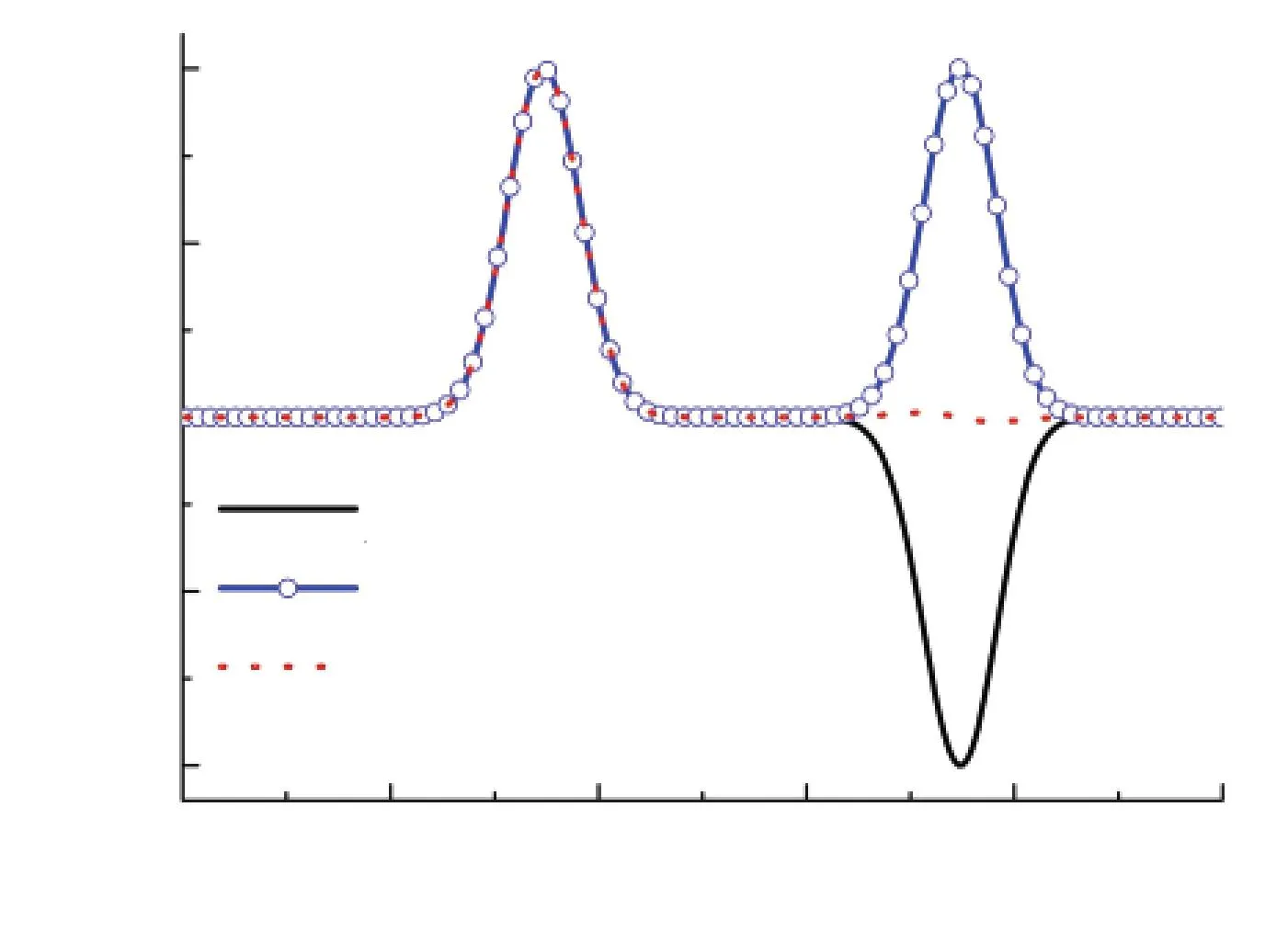
(a)显格式

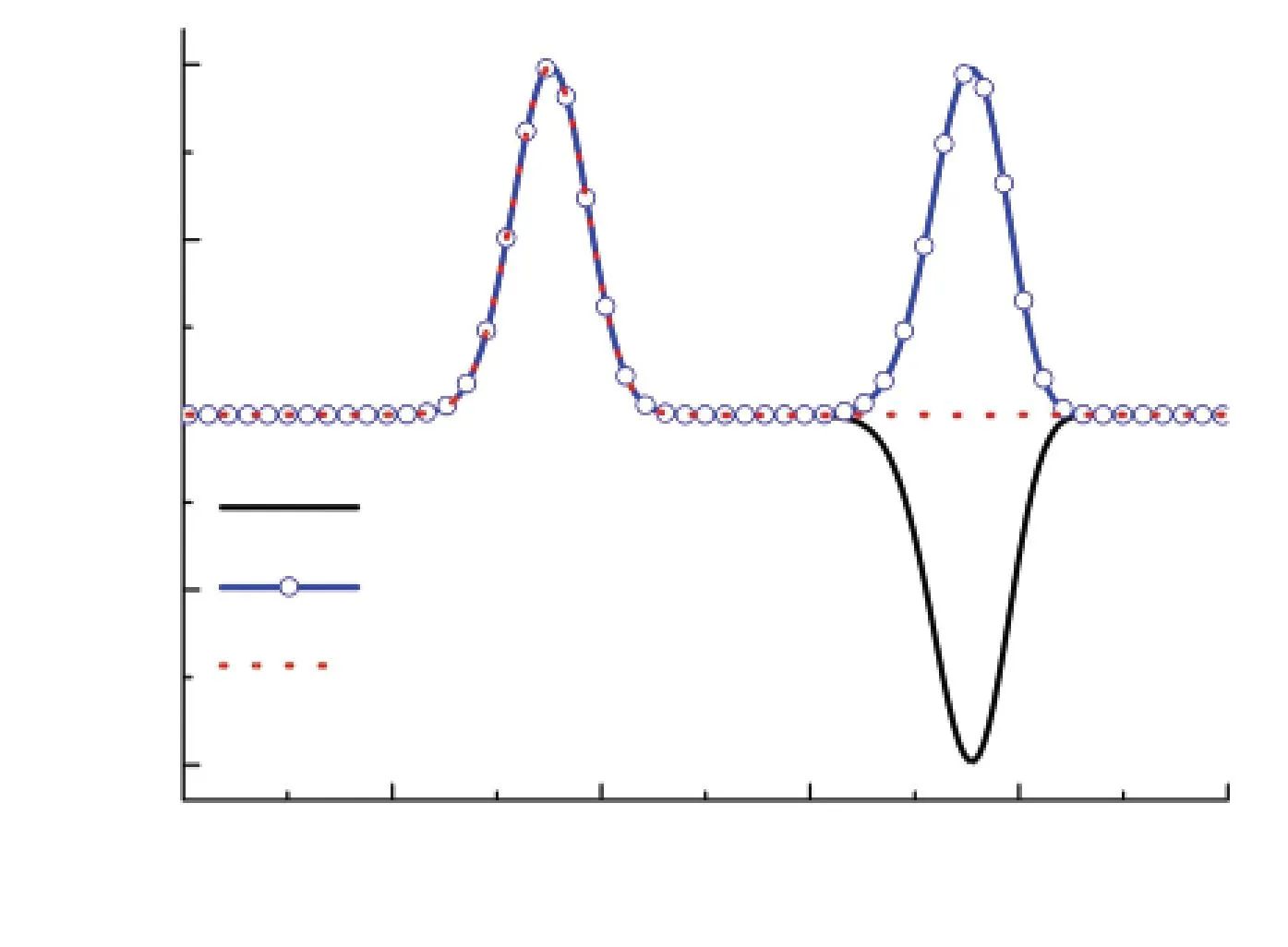
(b)隐格式

图7　不同边界条件时两种格式绝对误差的比较

4结论

1) 讨论了空间步长的影响. 当λ/Δx≥10后,显格式算法与隐格式算法均能够达到满足精度要求的解,并且随着网格的加密,计算结果保持不变;两种格式在内存消耗上比较接近,但在采用相同时间步长的前提下,显格式耗费较少的CPU时间．

2) 讨论时间步长的影响. 显格式算法是条件稳定的,当(c0Δt)/dx≤1.0时,计算结果稳定,而不满足此条件时计算会快速发散,这与理论推导的结果一致. 隐格式Newmark算法是无条件稳定的,当ω0Δt≤0.3时,所预测声压的相对峰值误差<1%,当ω0Δt>0.5时,所预测声压级的相对峰值误差会超出工程上±0.5 dB的误差需求．

3) 对于文中提到的全反射边界和吸收边界条件,两种算法均能够提供峰值误差<2%的数值解;显格式算法所得的入射波精度高于隐格式算法;对全反射边界条件的处理,显格式算法处理的精度高于隐格式算法;对吸收边界条件的处理,显格式算法处理的精度低于隐格式算法．

参考文献

[1] MANEERATANA K. Development of the finite volume method for non-linear structural applications[D]. London: the University of London, 2000.

[2] FOGARTY T R, LEVEQUE R J. High-resolution finite-volume methods for acoustic waves in periodic and random media[J]. Journal of the Acoustical Society of America, 1999, 106(1): 17-28.

[3] DEL-PINO S, DESPRÉS B, HAVÉ P, et al. 3D Finite Volume simulation of acoustic waves in the earth atmosphere[J]. Computers & Fluids, 2009, 38(4): 765-777.[4] 宁方立, 张文治, 董梁. 圆柱形谐振管内非线性驻波的有限体积计算方法[J]. 机械工程学报, 2012, 48(16): 116-121.

[5] 宣领宽, 张文平, 明平剑, 等. 预测消声器声学性能的时域非结构有限体积法[J]. 哈尔滨工程大学学报, 2012, 33(2): 185-191.

[6] 刘恒, 廖振鹏. 波动数值模拟的一种显式方法——二维波动[J]. 力学学报, 2010, 42(6): 1104-1116.

[7] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2001.

[8] 李太宝. 声场的方程和计算方法[M]. 北京: 科学出版社, 2005.

[9] 宣领宽, 张文平, 明平剑, 等. 基于不同时间步长时域非结构有限体积法模拟声-弹性耦合问题[J]. 固体力学学报, 2013, 34(2): 158-168.

[10]TAYLOR G A, BAILEY C, CROSS M. A vertex-based finite volume method applied to non-linear material problems in computational solid mechanics[J]. International Journal for Numerical Methods in Engineering, 2003, 56(4): 507-529.[11]王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.[12]宣领宽, 明平剑, 龚京风, 等. 三维各向异性功能梯度材料的有限体积法[J]. 哈尔滨工业大学学报, 2014, 46(7): 95-100.

[13]赵倩. 新型差分格式TDFEM及其腔体屏蔽效能分析研究[D]. 南京: 南京航空航天大学, 2011.

[14]GILES M B. Stability and accuracy of numerical boundary conditions in aeroelastic analysis[J]. International Journal for Numerical Methods in Fluids, 1997, 24 (8): 739-757.[15]明平剑. 基于非结构化网格气液两相流数值方法及并行计算研究与软件开发[D]. 哈尔滨: 哈尔滨工程大学, 2008.[16]李亚智, 赵美英, 万小朋. 有限元法基础与程序设计[M]. 北京: 科学出版社, 2004.

[17]倪大明. 非结构化网格FVM在流体动力声学计算中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

(编辑杨波)

An implicit finite volume method for the acoustic wave equation

XUAN Lingkuan1, GONG Jingfeng1, ZHANG Wenping2, YUAN Xingjun1

(1. China Ship Development and Design Center, Wuhan 430064, China;2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract:An implicit finite volume method (FVM) with Newmark scheme is proposed for the sound propagation problem, and it is used to simulate the propagation of the plane wave. By comparing to the results from the FVM with that of explicit central difference algorithm, the numerical error, stability and computational consumption are analyzed. It is shown that both methods can acquire accurate numerical solutions when λ/Δx≥10. The relative peak error of the implicit scheme is less than 1% when ω0Δt≤0.3. With the same time step and spatial step, the numerical result of the implicit scheme agrees better with the exact result. The implicit method treats the absorbing boundary condition more accurate than the explicit method, but it is reverse for the total reflecting boundary condition. The two methods consume similar memory and the explicit method consumes less CPU time.

Keywords:finite volume method; difference scheme; Newmark scheme; acoustic wave equation; plane wave

doi：10.11918/j.issn.0367-6234.2016.07.024

收稿日期:2015-06-13

基金项目:国家自然科学基金(51509232)

作者简介:宣领宽(1987—),男,博士,工程师

通信作者:龚京风, gongjingfeng@126.com

中图分类号:O422

文献标志码:A

文章编号:0367-6234(2016)07-0145-05