放松限购政策对住宅价格的空间效应研究

张海永

(1.中国矿业大学　管理学院，江苏　徐州　221116；2.滁州学院　数学与金融学院，安徽　滁州　239000)

放松限购政策对住宅价格的空间效应研究

张海永1,2*

(1.中国矿业大学管理学院，江苏徐州221116；2.滁州学院数学与金融学院，安徽滁州239000)

摘要：面对房地产市场库存高企、成交萎缩、房价下跌，地方政府实施放松限购政策以期缓解楼市转冷态势，关于放松限购政策影响住宅价格的空间计量研究相对匮乏。选取南宁市房地产市场数据，利用Moran’s I检验住宅价格的空间依赖性，把分位数回归方法引入空间滞后模型分析住房放松限购政策的空间异质性效应。研究发现实施放松限购政策在住宅价格分布的各个分位点处驱动房价上涨的效应不明显。政府应适时取消限购措施，通过市场化的手段促进房地产市场理性回归，发挥市场在资源配置中的决定性作用，构建房地产调控长效机制。

关键词：放松限购；房价；空间滞后依赖；分位数回归

目前国内对房地产市场放松限购政策的研究，主要是通过在媒体、报端等以文字评述的方式对放松限购政策实施的背景、范围、原因、作用、发展方向等进行简要描述或理论分析，缺乏严谨的理论模型及实证检验。南宁是首个由官方发文放松限购的城市，主要针对户籍限购进行放宽，使得可以在南宁市购房的潜在客户增多[1]。通过检验南宁房地产市场放松限购政策的效果，对其他城市而言具有借鉴作用。本文使用Moran’s I检验南宁房地产市场住宅价格的空间依赖性，判断是否需要考虑住宅价格的空间自相关因素，然后把分位数回归方法嵌入空间滞后模型研究松绑限购政策在住宅价格分布不同分位点处的空间效果，以期能够补充这方面的定量研究，为房地产市场相关政策的制定提供参考。

1指标选取

放松限购政策有利于释放住房需求，刺激住房成交套数上升，由此带来成交面积上升，商品房需求量增大诱发房地产价格上升[2]。因此，可以认为住房成交套数是放松限购政策影响房价的桥梁。选取地区虚拟变量(描述区域位置因素对房价的影响)和住房成交套数为解释变量。南宁市共6个城区，为避免虚拟变量陷阱，地区虚拟变量分别表示为X1(属青秀区取1，否则取0)、X2(属兴宁区取1，否则取0)、X3(属江南区取1，否则取0)、X4(属西乡塘区取1，否则取0)、X5(属良庆区取1，否则取0)，X6表示住房成交套数。以住房价格的对数形式ln y作为被解释变量[3-4]。以住房成交面积衡量区域房地产规模，空间滞后模型中权重矩阵W以房地产规模的距离为基本元素，利用高斯核函数进行构造[5-6]。

2数据来源

房地产市场的繁荣程度直接影响着当地的经济状况，南宁放松限购在很大程度上是为了提高日益下降的房价促进地方经济水平上升。从南宁发文放松限购2014年4月25日至9月30日央行松绑房贷期间，南宁的房地产市场不曾出现国家或地方的房地产新政，所以在这段时间内能够促进南宁房价上涨的驱动力因素基本上是放松限购，与之前旨在给房地产市场降温遏制房价上涨的密集宏观调控政策关联甚微。因此，本文选取2014年4月25日至9月30日南宁房地产市场每日的交易数据进行分析，数据来源于房王数据中心[7]和南宁市统计局。

3住宅价格空间依赖性检验

Kostov指出空间固定资产之间存在着潜在的空间依赖性[8]，Liao等使用空间滞后分位数回归模型研究长沙市房地产市场，结果发现房价具有空间依赖性[4]。南宁市6个城区住宅价格的全局Moran’s I及检验结果见表1。

表1　全局Moran’s I及检验

从表1可知，南宁市住宅价格整体上存在显著的空间依赖性，需要考虑纳入空间依赖因素的计量经济模型，上述3种空间计量经济模型：空间滞后模型、空间误差模型、空间通用模型，究竟哪种模型更恰当还要通过相应的判别准则进行确定。

4空间模型选择

当探测到数据的空间依赖性之后，无法根据经验判断哪种空间计量经济模型更适合于实际应用。本文通过比较3种模型空间参数估计值在统计上的显著性及赤池信息准则(AIC)判断哪一种空间计量经济模型更合适[9]，比较结果见表2。

表2显示，空间滞后模型(SLM)的空间影响系数ρ=0.341 9，P=0.005 280 1，非常显著，说明邻近区域的住宅价格对本地住宅价格产生了空间影响；SLM残差项空间依赖性的拉格朗日乘子检验值=1.275 7，对应的P=0.258 71，不显著，表明纳入邻近区域的空间影响之后，模型的残差项不存在空间依赖；空间滞后模型的赤池信息准则AIC为-459.72，小于普通线性模型的-457.22，说明在加入空间滞后项之后，模型的拟合程度有所改善。空间误差模型(SEM)的空间影响系数λ=0.143 75，其P=0.334 75，不显著，说明误差项的空间依赖性不明显；空间误差模型的赤池信息准则AIC为-455.9，大于普通线性模型的-457.22，说明前者在拟合程度上与后者相比没有改善，选择空间误差模型是不恰当的。空间通用模型(SAC)的空间滞后影响系数ρ=0.435 12，P=0.0487 55，在0.05水平上显著；空间误差影响系数，P=0.555 93，不显著，再次表明误差项的空间依赖性不强，考虑空间误差模型作用不大；空间通用模型的赤池信息准则AIC为-458.31，小于普通线性模型的-457.22，说明前者与后者相比较，空间通用模型在拟合程度上有改善。但是与空间滞后模型的赤池信息准则(AIC为-459.72)相比较，空间滞后模型在拟合性能上是更恰当的选择。为了获得解释变量在各个分位数水平上对住宅价格所起的不同作用，优化处理误差项的异方差性，应用两阶段分位数回归方法(2SQR)估计空间滞后模型，即选择空间滞后分位数回归模型来进行研究。

表2　空间参数估计与AIC

注：符号“-”表示相应空间模型回归结果中不含该项。

5估计结果

空间滞后分位数回归模型各变量系数的2SQR回归结果如表3所示。

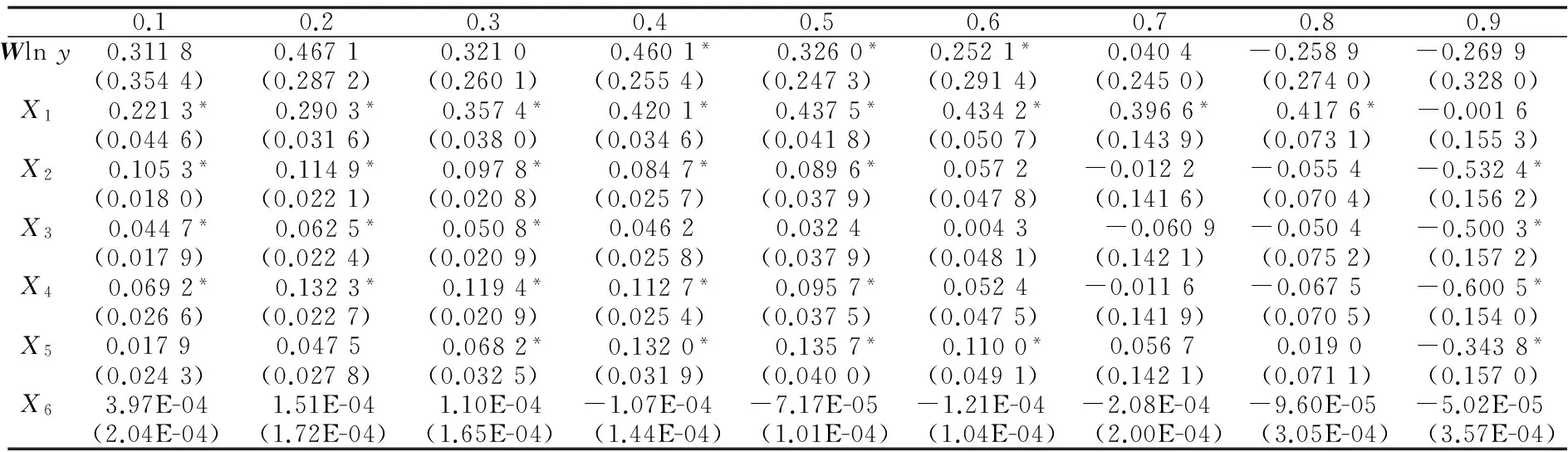
表3　2SQR回归结果

注：括号内的数字为Bootstrap标准差，*表示P<0.05的显著性水平。

空间滞后项对房价的影响在0.4～0.6分位点显著，在其他各分位点不显著。整体上看，房产价格受邻近房价的影响不明显，这与以往的研究结果有些差异，可能是因为南宁房地产市场库存高企、供大于求、销量萎缩，在信贷从紧的大环境下开发商为了快速回笼资金以价换量，不会过多参考邻近地区房价，房价的空间依赖性减弱。

地区变量对不同水平房价的影响差异明显。表3显示青秀区(X1)在0.1～0.8的分位点下对房价的影响显著，系数估计值随着分位点的升高先变大再变小，在0.5分位点处达到最大。兴宁区(X2)、西乡塘区(X4)在0.1～0.5及0.9分位点影响显著，且在0.9分位点处系数估计值为负数。江南区(X3)在0.1～0.3及0.9分位点处对房价影响显著，0.9分位点处的系数估计值为负数。良庆区(X5)在0.3～0.6及0.9分位点处影响显著，系数估计值先增再降，在0.5分位点处达到最大，在0.9分位点处达到最小(负数)。整体来看，各个城区的高端住宅价格(0.9分位水平房价)在南宁放松限购期间更容易下行。

如表3所示，住房成交套数(X6)在各分位点处对房价的影响不显著。这与南宁房地产市场庞大的库存有关，南宁楼市库存现状约644万m2，半年新增近100万m2，这个库存量大约需消化12个月左右[10]。供给远大于需求，供求力量悬殊，即使住房成交套数增加短期内也难以撼动库存，致使房价变化微弱。政府想通过放松限购政策刺激楼市交易回暖房价上涨，进而带动经济发展的初衷恐不能实现。

6结语

2014年以来许多城市的房价逐渐进入下行通道，房地产市场交易低迷，这对地方政府的财政收入和经济发展产生压力，地方政府采取放松限购政策以期能够转暖房地产市场。然而，放松限购政策对房地产市场的效果究竟如何？通过空间滞后分位数回归方法研究发现，住房成交套数对房价的影响非常微弱，说明放松限购政策难以驱动房价上涨。房地产行业过去10年的高速增长结束了住房普遍短缺、房企拿地就能赚钱的时代，透支了房地产市场未来若干年的增长潜力。当前的房地产市场库存压力大、成交萎缩、房价下降、增速放缓，购房者买涨不买跌的心态加重，市场观望情绪逐渐浓厚。放松住房限购政策在这种大环境下难以有效刺激住房需求入市，从而加剧了放松住房限购政策效果的微弱性。

2014年以来，房地产市场转冷既是对以往楼市过热的降温，也是对供不应求、房价过度上涨的调整。本轮调整并不是由政策引起，而是市场经济体制下楼市自发调整的正常现象。地方政府的行政职能不应该是过多干预楼市，而应该通过行政手段维护房地产市场的稳健运行，充分发挥市场在资源配置中的决定性作用。不能房价一降就急于救市， 因为发自市场本身的调整急于救市效果并不明显。所以，未来房地产的调控思路应该转向通过市场手段促进房地产市场的理性回归，政府与市场重新定位，政府要实现“去行政化”，稳步推进房地产行业发展的长期性制度变革，构建房地产调控长效机制，包括房地产税、土地制度、城镇化战略等。

参考文献：

[1] 清远市人民政府.广西北部湾经济区其他城市居民可享同等购房政策[EB/OL].(2014-04-30)[2014-5-05].http://www.gdqy.gov.cn/.

[2] 闫绪娴,夏恩君.北京市普通住宅商品房销售面积预测[J].北京理工大学学报(社会科学版),2002(S1): 88-90.

[3] ZIETZ J,ZIETZ E N,SIRMANS G S. Determinants of house prices: a quantile regression approach[J].The Journal of Real Estate Finance and Economics,2008,37(4):317-333.

[4] LIAO W C,WANG X.Hedonic house prices and spatial quantile regression[J].Journal of Housing Economics,2012,21(1):16-27.

[5] 林光平,龙志和,吴梅.我国地区经济收敛的空间计量实证分析:1978—2002年[J].经济学(季刊),2005(S1):67-82.

[6] 杨康,李满春,刘永学,等.基于累积相似度表面的空间权重矩阵构建方法[J].测绘学报,2012,41(2):259-265,272.

[7] 房王数据中心.南宁住宅实时成交数据[DB/OL].(2014-04-20)[2014-10-05].http://nn.data.ihk.cn/.

[8] KOSTOV P.A spatial quantile regression hedonic model of agricultural land prices[J].Spatial Economic Analysis,2009,4(1):53-72.

[9] 王庆喜,蒋烨,陈卓咏.区域经济研究实用方法:基于ArcGIS,GeoDa和R的运用[M].北京:经济科学出版社,2014.

[10] 南国城报一居周刊.南宁楼市库存调查[EB/OL].(2014-04-20)[2014-10-05].http://epaper.gxnews.co m.cn/ngcb/html/2014-11/27/content_2499444.htm.

Research on the Spatial Effect of Loosened Home-buying Restrictions on Housing Prices

ZHANGHaiyong1, 2*

(1. School of Management, China University of Mining and Technology, Xuzhou 221116, China; 2. School of Mathematics and Finance, Chuzhou University, Chuzhou 239000, China)

Abstract:Local governments loose home-buying restrictions to try to solve the problems of high inventory, shrinking deal and falling house prices in China’s housing markets. The spatial effect of loosened home-buying restrictions on housing prices attracts much attention, on which the quantitative research is relatively scarce. This article takes Nanning’s housing market as an example, then uses Moran’s I to test the spatial dependence in housing prices, and incorporate spatial lag model with quantile regression to analyze the effect of loosened home-buying restrictions on housing prices. Our results reveal that loosened home-buying restrictions is hard to push housing prices up at all quantiles of the distribution of housing prices, which suggests that government should cancel home-buying restrictions in good time, promote the rational regression of housing market by means of marketing, let market play a decisive role in the allocation of resources and build long-term effective mechanism of housing regulation.

Key words:loosened home-buying restriction; housing price; spatial dependence; quantile regression

DOI:10.13542/j.cnki.51-1747/tn.2016.02.025

收稿日期：2016-03-10

基金项目：江苏省普通高校研究生科研创新计划项目“基于空间分位数回归模型的房价异质性及调控政策研究”(KYZZ_0384)；滁州学院科研项目“基于时变非对称嵌套权重矩阵的房价贝叶斯空间分位数回归模型与实证研究”(2015GH25)

作者简介：张海永(1981— )，男(汉族)，江苏徐州人，讲师，在读博士研究生，研究方向：空间分位数回归与房价建模，通信作者邮箱：haiyongzhangcumt@foxmail.com。

中图分类号：F293.35

文献标志码：A

文章编号：2095-5383(2016)02-0090-03