“不等式及其解集”教学设计

周秀珍



“不等式及其解集”教学设计

周秀珍

一、情境引入

多媒体出示问题：一辆匀速行驶的汽车在11：20距离A地50千米，

问题1：要在12：00到达A地，车速应满足什么条件？

问题2：要在12：00之前驶过A地，车速应满足什么条件？

学生讨论发言后，师生共同分析解决问题。

二、合作探究

问题3：汽车到达A地需要行驶多长时间？在11:20～12:00，汽车驶过的实际路程是多少？

问题4：设车速是x千米/时，

（1）从时间上看，汽车要在12：00之前驶过A地，则以这个速度行驶50千米所用的时间不到小时，如何表示这种数量关系？

（2）从路程上看，汽车要在12：00之前驶过A地，则以这个速度行驶小时的路程要超过50千米，如何表示这种数量关系？

教师引导学生总结不等式的概念。在概念辨析环节，学生先举例，再判断其是否为不等式，明确所有用不等符号连接的式子都是不等式。

三、分解难点

问题5：要使汽车在12：00之前驶过A地，你认为车速应满足什么条件？车速可以是78千米/时吗？75千米/时呢？72千米/时呢？

问题6：我们知道“使方程两边相等的未知数的值是方程的解”，那么我们可以把使不等式成立的未知数的值叫做什么？

请各组说出一个满足上述不等式的数，引导学生观察各组所选数值的差异。师生共同归纳，类比方程的解进行教学，引出不等式的解的概念。

前面学的方程的解一般只有一个，今天所学的不等式的解却不只一个。引导学生理解不等式的解与解集的联系与区别。

学生分组讨论，各组找出几个能满足该不等式的值。教师引导学生发现各组所选数值的差异并找出规律。经过刚才的分析，可以知道，要使汽车在12：00之前驶过A地，车速必须大于75千米/时。所以这个不等式的解集是什么？你能在数轴上把它表示出来吗？

学生动手，教师示范。

四、突破难点

问题8：x＞75表示x可以取哪些数？

在数轴上表示大于75的数的点应该在数75所对应点的左边还是右边？（右边）因此我们可以在数轴上把x＞75直观地表示出来。画图时要注意方向（向右）和端点（不包括数75，在对应点画空心圆圈）。

归纳：用数轴表示不等式的解集分三步：（1）画数轴；（2）定界点；（3）定方向。

问题9：如果不等式的解集为x≤-2，那么它表示x可取哪些数？

将不等式x≤-2用数轴表示时，包括-2这个对应点，因而在该点处画实心圆点（如图所示）。

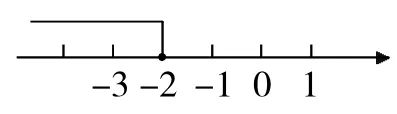
引导学生总结在数轴上表示不等式解集的要点：小于向左画，大于向右画；无等号画空心圆圈，有等号画实心圆点。

五、大显身手

1.在数轴上表示下列不等式的解集。

（1）x＜3；（2）x≤-4；（3）x≥0；（4）-1≤x；（5）x+3＞6。

2.将数轴上x的范围用不等式表示。

3.用不等式表示下列数量关系，再用数轴表示出来。

（1）x小于-1；（2）x不小于-1；（3）a是正数；（4）b是非负数。

六、归纳巩固

不等式解集的表示方法：

1.代数表示（x＞a，x＜a，x≥a，x≤a）

2.几何表示（数轴表示法）

用数轴表示不等式的解集分三步：（1）画数轴；（2）定界点；（3）定方向。

（作者单位：衡阳市第九中学）