基于迭代优化算法的MVDR空间谱估计的SoC实现

廖　斌，李思敏，2,唐智灵,2

(1.桂林电子科技大学 信息与通信学院,广西 桂林　541004；2.桂林电子科技大学 认知无线电与信息处理教育部重点实验室，广西 桂林　541004)

基于迭代优化算法的MVDR空间谱估计的SoC实现

廖斌1，李思敏1，2,唐智灵1,2

(1.桂林电子科技大学 信息与通信学院,广西 桂林541004；2.桂林电子科技大学 认知无线电与信息处理教育部重点实验室，广西 桂林541004)

摘要：针对MVDR算法中矩阵求逆运算量大、耗时长，提出一种基于迭代优化的坐标下降法。该算法将逆矩阵求逆转化为线性方程组的最优解，以迭代的方式代替传统的矩阵运算。同时采用FPGA的SoC设计方式，在处理器上搜索谱峰，并通过专门的硬件实现迭代优化算法，以加速求逆运算。仿真结果和硬件测试表明，计算结果与实际结果的误差很小，基于SoC的设计能有效地搜索出谱峰。

关键词：阵列信号处理；MVDR；DOA；逆矩阵；SoC

来波方向(direction of arrival,简称DOA)估计主要用于测量入射信号的来波方位。在智能天线应用中，一旦有了信号的方位信息，就可以根据需求判断是否将最大波束对准该方向。而在电子侦查中，则可以通过来波方位信息对辐射源定位，以确定辐射源的相对位置[1]。

典型的测向算法有MUSIC(multiple signal classification)算法、ESPRIT(estimate signal parameter via rotational invariance techniques)算法以及MVDR(minimum variance distortionless response)算法。其中，MUSIC算法利用信号子空间和噪声子空间的正交性，构建空间谱函数[2]；ESPRIT算法利用自相关矩阵信号子空间的旋转不变特性构建空间谱函数[3]；而MVDR算法是在MVDR波束成形基础上得到的空间谱函数，该波束成形是在保持期望信号增益不变的情况下，使其他观测方向的输出平均功率最小[4]。

通常基于MVDR的DOA估计需要完成协方差的求逆运算，而典型的求逆方式是采用一种基于systolic结构的QR分解算法[5-7]，通过并行运算减少处理时间。但是，由于占用了大量的矩阵运算，使其消耗更多的硬件资源。为此，提出一种基于迭代优化的坐标下降法，通过求解线性方程的迭代最优解代替矩阵的分解运算，减少硬件资源，缩短运算时间。同时，为了便于完成谱峰搜索，采用FPGA的SoC(system on chip)设计方案，利用基于迭代优化算法的硬件IP核完成求逆加速运算，并通过软件的方式进行谱峰搜索算法的处理，简化了硬件设计。

1相关工作

1.1阵列信号模型

假设由N个阵元组成均匀线阵，线阵间距为d，若有D个窄带信号sk(t),k=1,2,…,D入射,其对应来波方向θk=(θ1,θ2,…,θD)，则第i个阵元接收到的信号:

(1)

其中：ni(t)为第i个阵元的加性噪声；λ为信号波长。

整个阵列接收的信号表示为:

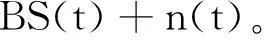
(2)

阵列的加权输出：

(3)

其中w=[w1,w2,…,wN]T。

1.2基于MVDR的DOA估计

MVDR是一种最小方差法，其在信源方向θk上信号功率不变，而非信源方向的任何干扰所贡献的功率为最小，即

(4)

根据Lagrange乘数法，可得

(5)

其中Rxx为阵列的协方差矩阵，有

(6)

实际处理中，无法得到理想的协方差矩阵，通常采用最大似然估计：

(7)

其中：x(n)=[x1(n),x2(n),…,xN(n)]T为第n时刻阵元的输出，称为一次快拍；K为快拍数。

根据式(4)，可得空间功率谱函数：

(8)

DOA估计就是对所有θ进行式(8)的计算，得到每个角度对应的功率，并搜索其谱峰，谱峰对应的角度就是其波达角。

1.3坐标下降法

根据式(7)，设x=R-1a(θ)，则有Rx=a(θ)，可得

(9)

因此，可将MVDR的求逆变换为线性方程组Rx=a(θ)的求解。

求解线性方程组有直接法和迭代法，其中，坐标下降法是求解线性方程组的一类迭代算法，其基于准确线性搜寻方式来求解线性方程组Ax=b，A∈RNN的通用算法步骤如下[8]：

1)r(0)←b-Ax(0)，p(k)←f(k)，一般取x(0)=0。

2)Fork=1,2,…

其中：a(k)为搜索步径；p(k)为搜索方向矢量。

令p(k)=p(k+N)，且满足p(n-1)=en，n=1,2,…,N，en∈RN，其中en表示第n个元素为1、其余元素为0的单位列向量，可得坐标下降法，其有如下关系：

(10)

(11)

(12)

1)r(0)=b-Ax(0)，p(0)=e1，k=0，x(0)=0。

2)Forn=1∶N

k=k+1;

if( k>kmax)stop

End

2坐标下降法的迭代优化及仿真

2.1基于迭代优化的坐标下降法

(13)

(14)

故可得到基于迭代优化的坐标下降法的伪代码形式：

1)初始化变量：a(k)=2p，r=b，x=0，m=1，k=1，M、H为常数。

2)For m=1∶M

a(k)=a(k)/4;

For k=1∶H

For n=1∶N

xn=xn+sign(rn)a(k);

r=r-sign(rn)A:,n;

End

End

End

伪代码中的常数M为对搜索步径进行倍数缩放的次数，常数H为按确定步径进行搜索的次数。改进后的迭代优化算法，由于a(k)为2的倍数次幂，可用移位方式代替乘法器，故算法共用了N×(N+1)×H×M个加法，而之前的坐标下降法共用了(N+1)×k个加法、N×k个乘法、k个除法。

(15)

其中：

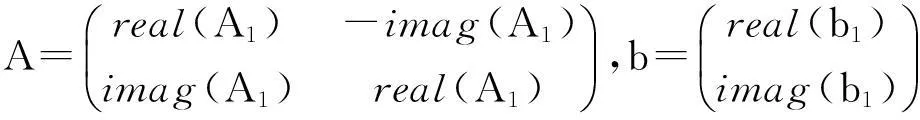
2.2迭代优化算法的仿真

仿真条件：由四阵元构成均匀线阵，载波频率为15 MHz，间距d=10 m，快拍数K=256，有2个信号源，入射角度分别为-10°、25°。改进的坐标下降法的初始步径设为a(k)=2。

图1、图2为不同迭代参数下迭代优化算法和基于Matlab直接求逆函数的空间谱。由图2可知，当参数M=8，H=8，基于迭代优化的坐标下降法的计算曲线几乎与理论的数值曲线重合，即迭代优化算法的计算结果与理论计算值误差很小。比较图1和图2可得，迭代算法的参数M、H影响计算结果的准确性，M和H的值越大，计算结果越接近理论值。

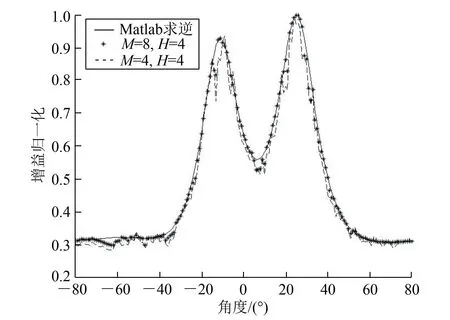
图1　MVDR空间谱(H=4)Fig.1　MVDR spatial spectrum(H=4)

图2　MVDR空间谱(H=8)Fig.2　MVDR spatial spectrum(H=8)

3DOA估计的SoC设计

3.1总体方案

图3为基于FPGA的DOA的SoC构架，通过AXI总线实现软核处理器Microblaze与片上外设的数据通信，其中，在FPGA的逻辑部分完成基于最大似然估计的协方差模块的IP核、基于优化迭代算法的IP核的设计，而在软核处理器上谱峰搜索，通过求极小值得到其谱峰，并在每搜寻一个角度时，调用迭代优化算法的IP核完成求逆的硬件加速，而其他外设如UART(串口)，则负责程序的调试，定时器计算程序运行时间。

图3　基于FPGA的DOA SoC构架Fig.3　SoC architecture of DOA based on FPGA

3.2协方差模块的IP核设计

根据式(7)，协方差矩阵可写成：

基于AXI总线协方差模块的IP核设计如图4所示，快拍数设K=2q,q∈N，其中AXI Bram Control主要完成AXI总线地址与Dual RAM(双端口RAM)地址的转换。IP核的软硬件协同工作如下：

1)处理器通过AXI总线读取IP核的状态寄存器中的busy位，判断其是否为1，若是，则等待，直到busy=0，跳转至下一步。

2)往寄存器K写入快拍数，并使能控制寄存器的start位，使能有效后，双端口RAM的R1数值将清零，AD采样模块开始工作，接收当前的快拍，并从双端口RAM x的A口写入，在下个周期从B口读出送入MUY Writer模块，经过相乘得到串行x(n)x(n)H，并与从双端口RAM R1的B口读出的数值R1(n-1)相加，得到新值。之后从A口回写,覆盖双端口RAM的R1数值，双端口RAM的R1主要功能是存储累加的数值，直至K-1次累加后，送入桶形移位寄存器进行q位右移，移位后所得数据从A口写入存放复数协方差的双端口complex RAM中，最后根据式(15)，通过一个RAM Control模块，将复数协方差RAM的数值转换成实数，并写入实数协方差双端口real RAM中。

3)直到状态寄存器的finish=1，通过总线读取实数协方差双端口RAM的数值。

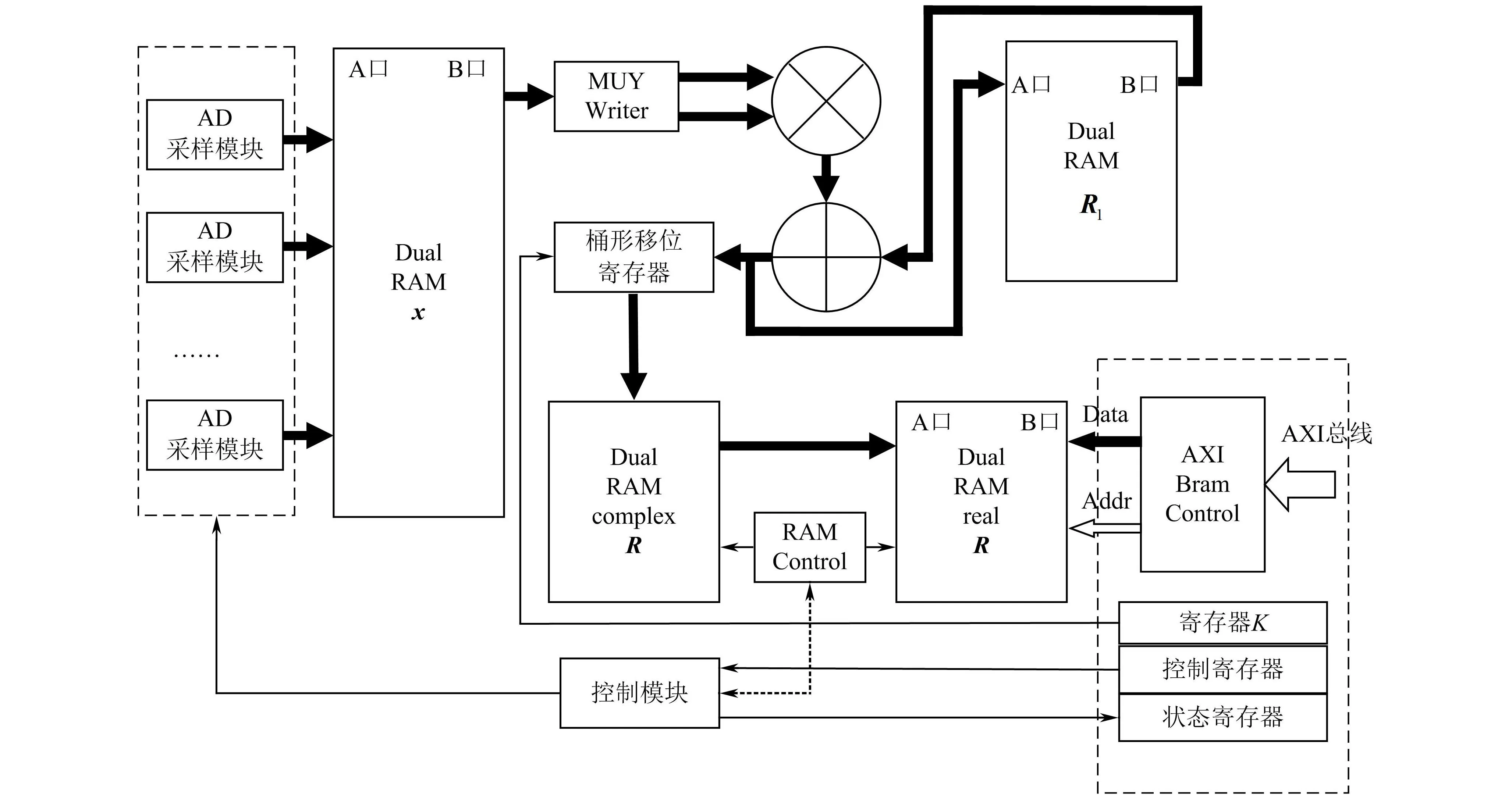
图4　协方差模块的IP核设计Fig.4　Design of covariance module IP core

3.3基于迭代优化算法的IP核设计

图5为迭代优化算法的实现框图,以求解Ax=b,A∈RNN，其中，图5的双端口RAM r的初值为b，状态机负责模块的协调工作。整个IP核的软硬件协同工作如下：

1)处理器通过AXI总线读取IP核的状态寄存器中的busy位，判断其是否为1，若为1，则一直等待，直到busy=0，跳转至下一步；

2)通过总线在双端口RAM A写入协方差矩阵、双端口RAM r写入方向矢量，并将双端口RAM x清零；

3)寄存器M、H写入迭代数值，寄存器a(k)写入初始步径，并使能控制寄存器的start位，使状态机开始工作，直到状态寄存器的finish=1，通过AXI总线将双端口RAM x的值读出。

状态机的工作流程为：

1)状态机一开始处于idle状态，直到start信号为高，状态机由idle状态转为state0，计数器m置0；

2)当状态处于state0，判断计数器m是否小于寄存器M，若是，则状态跳转到state1，计数器k置0，寄存器a(k)右移2位，否则，状态跳转到idle，状态寄存器finish置1；

3)当状态处于state1，判断计数器k是否小于寄存器H，若是，则状态跳转到state2，计数器n置0，否则，状态跳转到state0状态，计数器m加1；

4)当状态处于state2，判断计数器n是否小于N，若是，则跳转到state3，否则，状态跳转到state1，计数器k加1；

5)当状态处于state3，判断done信号是否为高，若是，则状态跳转到state2，否则状态一直维持在state3。

state3的工作主要是完成xn=xn+sign(rn)a(k)与r=r-sign(rn)a(k)A:,n的计算。如图5所示，分别从双端口RAM A和双端口RAM r的B口读取当前的A:,n与r，放入受控于当前a(k)的桶形移位寄存器得到a(k)A:,n，将a(k)A:,n和取反后的-a(k)A:,n送入二选一多路复用器，rn的最高位连接到二选一多路复用器的选择端，当rn为正(最高位为0)，多路复用选择的输出为-a(k)A:,n，当rn为负(最高位为1)，选择的输出为a(k)A:,n，故多路复用器的输出可表达为-sign(rn)a(k)A:,n，再将多路复用器的输出与r相加得到新的r值，再从双端口RAM r的B口回写，覆盖原来的值。

同理，rn的最高位连接到第2个多路复用器的选择端，当rn为正，多路复用选择的输出为a(k)，当rn为负数，选择的输出为-a(k)，故多路复用器的输出可表达为sign(rn)a(k)，最后将多路复用的输出与从双端口RAM x的B口读取的xn相加得到新值，再从双端口RAM的B口回写，覆盖原来的值。

图5　基于迭代优化算法的IP核设计Fig.5　Design of IP core based on iterative optimization algorithm

从图5可看出，影响IP核最高时钟频率的关键路径是2个多路复用器的输出与加法器、桶形移位寄存器输出与第一个多路复用器的输入，因此，需在上述关键路径中插入触发器D，以提高最高运行时钟频率。

基于迭代优化算法的IP核在Xilinx的Kintex 7 xc7k160t芯片上完成了验证。其中，双端口RAM A的元素用32 bit的有符号整数表示，双端口RAM r和x的元素均用32 bit定点有符号数表示，小数位占20 bit。根据综合布线结果，表1为迭代优化算法与其他算法的所耗硬件资源对比，其中，迭代优化算法的迭代参数为a(k)=2，M=8，H=8。从表1可看出，基于改进的迭代算法虽然所需处理时间并不一定是最优的，但是它能以更少的资源获得更小的处理延时。同时，需要注意的是，由于迭代优化算法在实现的过程中采用的是一种串行流水线的结构，故无论矩阵的维数是多少，其所消耗的主要硬件资源差别不大，不同之处是处理所消耗的时间。

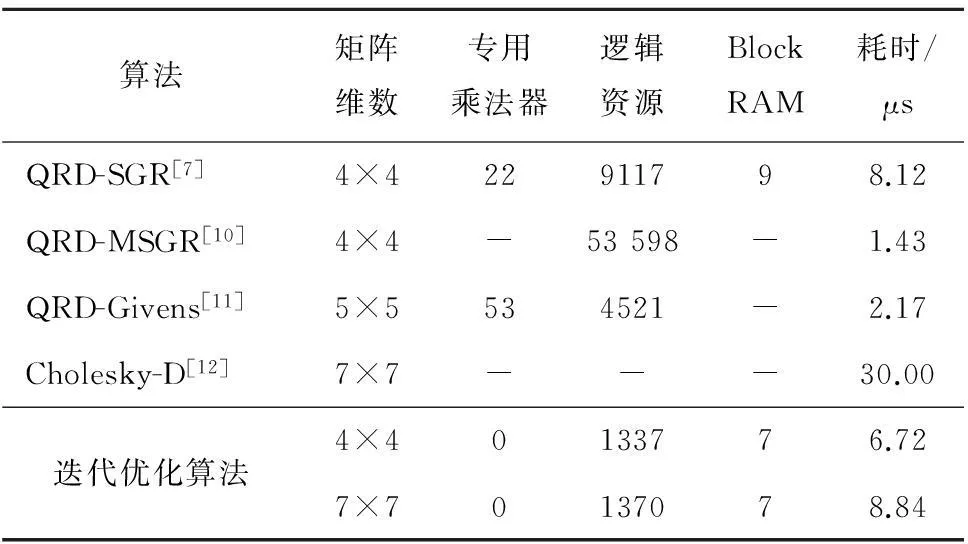
表1　优化迭代算法与其他算法的硬件资源对比

3.4DOA估计的软硬件协同设计

波达角的估计可认为是极小值的搜寻，即在整个空间谱上找出所有的极大值[7]，再找出大于某个给定数值的极小值，则其对应的角度就是波达角。根据式(8)，MVDR空间谱表达式的分子为1，因此，可将DOA估计转化为寻找a(θ)HR-1a(θ)在所有角度θ上的极小值，并满足小于某个门限值Q。在软件处理时，为了减少处理器的运算时间，预先定义一组8位有符号的常数组存放每个角度对应的方向矢量，该方向矢量是由a(θ)归一化后的数值进行127倍放大，并经过式(15)转换的实数方向矢量。DOA估计软硬件协同的程序伪代码如下：

1)定义数组c，存放空间谱的功率值。定义常数组存放方向矢量a(θ),θ=[-90°,90°]。

2)i=0,θ=-90°。调用协方差IP核求出协方差R。

4)i=1,θ=-89°,umin=q[0]。

while (θ≤90°)

{ 调用迭代算法IP核，计算当前x=R-1a(θ)；

if (c[i-1]≥c[i])

{umin=c[i]; }

i=i+1;θ=θ+1;

}

5) Q=2×umin,i=1;

while (i≤180°)

{ if (c[i]≤Q)

{ if (c[i-1]≥c[i])

{ y=c[i];z=i-90°;j=0; }

else

{j=j+1;

if (j= =1) 串口输出变量y、z的

值；}

}

i=i+1;

}

伪代码中的第4)步主要寻找空间谱的最小值，角度的步径为1°，并且每对一个角度求逆时，均要调用迭代优化算法的IP核，以减少运算时间。第5)步主要完成空间谱极小值的搜寻，其门限值Q设为最小值的2倍，并从串口输出变量z，该变量就是其波达角。

3.5硬件实验

测试条件：四阵元的均匀线阵，线距d=10 m，接收机接收15.702 MHz的调幅信号，而在远端5 km处发射一个同频干扰源，发射功率为3 W，方位角约为5°。

通过阵列接收机将四阵元的信号下变频至10 kHz处，并经过AD采样，在FPGA进行基带处理。根据改进坐标下降法的不同迭代参数得到表2，表2中M=8，H=8所对应MVDR的实测空间谱，如图6所示。

表2　不同迭代参数的数值统计

图6　基于MVDR的空间谱Fig.6　Spatial spectrum based on MVDR

图6和表2所用数据是由片上系统的UART模块输出，而表2中耗时统计则由片上系统的定时器进行估算。由表2和图6可知，2个信号的波达角为5°和43°，并且完成DOA估计所用时间约40 ms。同时，比较表2不同参数下所耗时间可知，由于求逆的迭代运算是用专门的硬件完成的，求逆矩阵需要的时间较短，故随着迭代次数的增加，其所耗时间相对处理器不会明显增加。

4结束语

为了完成DOA估计，简化FPGA的硬件设计，提出了一种基于FPGA的SoC的设计方案。通过软硬件协同设计，完成谱峰搜索算法实现。同时为了兼顾实时性，对坐标下降法进行改进，将求逆运算中的大量矩阵变换运算转换为线性方程组的最优求解，并用移位的方式代替乘法运算。数值仿真结果表明了该算法计算结果的正确性，并在FPGA上完成了迭代优化算法的IP核实现。根据综合布线后的结果，其能以较少的资源获得较短的运算时间。为了验证方案实际效果，搭建了整机测试平台。实验结果表明，基于SoC的设计方案能在40 ms内正确地测出信号的波达方向。在未来的波束成形芯片集成化中，该方案也具有一定参考价值。

参考文献:

[1]杨小牛．软件无线电技术与应用[M].北京：北京理工大学出版社，2010:459-461.

[2]WANG Qihui,WANG Lidong,KANG An,et al.DOA estimation of smart antenna signal based on MUSIC algorithm[J].Journal of Networks,2014,9(5):1309-1316.

[3]ROY R,KAILATH T.ESPRIT-Estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics Speech and Signal Processing,1989,37(7):984-995.

[4]CAPON J.High-resolution frequency-wavenumber spectrum analysis[J].Proceedings of the IEEE,1967,57(8):1408-1418.

[5]ZHANG Jianfeng,CHOW P,LIU Hengzhu.An efficient FPGA implementation of QR decomposition using a novel systolic array architecture based on enhanced vectoring CORDIC[C]//International Conference on Field-Programmable Technology,2014:123-130.

[6]朱勇旭，吴斌，周玉梅，等.用于MIMO-OFDM系统QR分解的分布式脉动阵列处理算法[J].电子与信息学报，2012,34(8):1963-1973.

[7]KARKOOTI M,CAVALLARO J,DICK C.FPGA implementation of matrix inversion using QRD-RLS algorithm[C]//Asilomar Conference on Signals,Systems,and Computers,2005:1625-1629.

[8]WATKINS D S.Fundamentals of Matrix Computations[M].New York:John Wiley Sons,2002:559-570.

[9]LIU Jie.DCD algorithm: architectures,FPGA implementations and applications[D].York:University of York,2008:37-45.

[10]MA L,DICKSON K,MCALLISTER J,et al.QR Decomposition-based Matrix inversion for high performance embedded MIMO receivers[J].IEEE Transcations on Signal Processing,2011,59(4):1858-1867.

[11]YU Hanguang.FPGA-based implementation of QR decomposition[D].Arizona:Arizona State University,2014:50-80.

[12]魏婵娟，张春水，刘健.一种基于Cholesky分解的快速矩阵求逆方法设计[J].电子设计工程，2014,22(1):159-164.

编辑：梁王欢

SoC implementation of MVDR spatial spectrum estimation based on iterative optimization algorithm

LIAO Bin1, LI Simin1,2, TANG Zhiling1,2

(1.School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin 541004, China;2.Key Laboratory of Cognitive Radio and Information Processing, Guilin University of Electronic Technology, Guilin 541004, China)

Abstract：Aiming at the large amount of calculation and time-consuming in matrix inversion of MVDR algorithm, a coordinate descent method based on iterative optimization is proposed. The matrix inversion is converted into optimum solution of a linear equation. Meanwhile, SoC design based on FPGA is adopted, the spectrum peaks are searched in the processor and the iterative optimization algorithm is implemented on the dedicated hardware for accelerating matrix inversion. The simulation result shows that the error between the calculated result and the actual result is very small. The hardware test shows that the SoC design can effectively search the peaks of the spectrum.

Key words：array signal processing; MVDR; DOA; matrix inversion; SoC

收稿日期：2016-01-16

基金项目：国家自然科学基金(61461013)

通信作者：李思敏(1963-)，男，江苏苏州人，教授，博士，研究方向为电磁场与电磁波、认知无线电。E-mail:siminl@guet.edu.cn

中图分类号：TN911.72

文献标志码：A

文章编号：1673-808X(2016)02-0087-07

引文格式： 廖斌，李思敏，唐智灵.基于迭代优化算法的MVDR空间谱估计的SoC实现[J].桂林电子科技大学学报，2016,36(2)：87-93.