Maple 软件在大学数学教学中的应用
2016-06-26孔祥强
孔祥强
(菏泽学院 数学系, 山东 菏泽 274015)
Maple 软件在大学数学教学中的应用
孔祥强
(菏泽学院 数学系, 山东 菏泽 274015)
Maple 软件是应用广泛的数学类软件,具有强大的数值计算和绘图功能.大学数学课程中引入Maple 软件进行教学,实现了教学内容的直观化、交互化.利用符号命令,通过编程,实现了复杂计算的快速化、复杂图形的准确作图,提高了教学效率并获得更好的教学效果.
Maple;数学软件;大学数学;绘图
Maple 软件是由加拿大 Waterloo 大学开发的数学类软件,具有强大的符号运算、图形绘制、数值计算功能,是一种交互式计算机代数系统[1].Maple软件的出现为大学数学的教学提供了轻松的教学气氛和有力的工具[2].从 1985 年出现的第一个商业版本 Maple3.3,到现在的 Maple18 版 本[3],Maple 软件得到了不断的更新和迅速的发展.
大学数学是学生的基础课,学好这门课的重要性不言而喻,但其内容比较抽象,概念难理解,题目计算繁琐.如果再按照传统的教学模式授课,学生难于接受.将 Maple 软件引入课堂,一方面可使得教师和学生从繁杂的计算中解脱出来,让学生的注意力主要集中在解题方法上;另一方面,将复杂、抽象的内容用软件演示出来,这种可视化的效果更能揭示问题的本质,从而提高学生学习的积极性,调动起学习的主动性,达到利用所学知识解决实际问题的目的[4].文章从 Maple 软 件 绘 制 平面图形和解微分方程两方面入手,深入探讨了 Maple 软件在大学数学教学中的应用,以期达到更好的教学效果.
1 Maple 软件在平面图形绘制中的应用
大学数学中,有很多极坐标曲线,如阿基米德螺 线 ρ=a·θ、 对 数 螺 线 ρ=ea·θ、 伯 努 利 双 纽 线ρ2=a2sin2θ、玫瑰线等,这些曲线的表达式并不复杂,但手工作图比较困难.而利用 Maple 软件,通过编程,很容易作出这些曲线的图形,并且通过图形可更好的了解曲线的性质.以玫瑰线为例,具体说明.
案例 1 作出曲线 ρ=2·sin(7θ)的图形[5].
玫瑰线的极坐标方程为 ρ=a·cos(n·θ)或 ρ=a· sin(n·θ),不妨取 a=2,n=7,程序如下


图1 七叶玫瑰线
由图 1,ρ=2·sin(7θ)的图形由七叶组成,故称为七叶玫瑰线.通过和案例 1 类似的程序可验证,当 n为奇数时,ρ=a·cos(n·θ)或 ρ=a·sin(n·θ)的图形均由n 叶组成,称为 n 叶玫瑰线;当 n 为偶数时,ρ=a·cos (n·θ)或 ρ=a·sin(n·θ)的图形均由 2·n 叶组成,称为2·n 叶玫瑰线.如 ρ=a·cos(5·θ)的图形是五叶玫瑰线,ρ=a·sin(6·θ)的图形是十二叶玫瑰线.n 可取正整数,还可取分数,甚至对于一些复杂的图形,n 可取无理数.如曲线 ρ=3·cos()的图形见图 2.

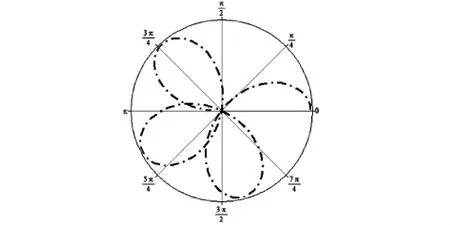
图2 曲线 ρ=3·cos()图形
内旋轮线是大学数字中非常重要的曲线[5].设有一大圆,当一小圆在大圆内滚动时,小圆上某一固定点的运行曲线,称为内旋轮线,有的教材上也称为内摆线.首先,曲线的参数方程比较复杂;其次,大圆半径 R 和小圆半径 r之间的数量关系不确定,仅知道 R>r.故内旋轮线的作图比较复杂.利用Maple 软件,可方便的讨论 R 和 r之间的倍数关系,作图快捷.
案例2 作出内旋轮线

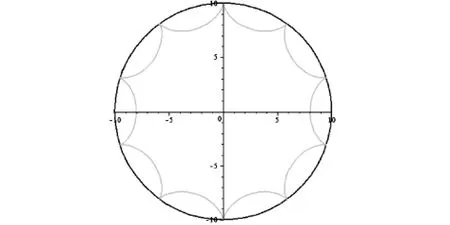
图3 R=10·r时的内旋轮线
特别地,当大圆和小圆的半径是4倍关系时,不妨取 R=4,r=1,此时得到图 4,即星形线[5].因此,星形线可看作内旋轮线的特例.

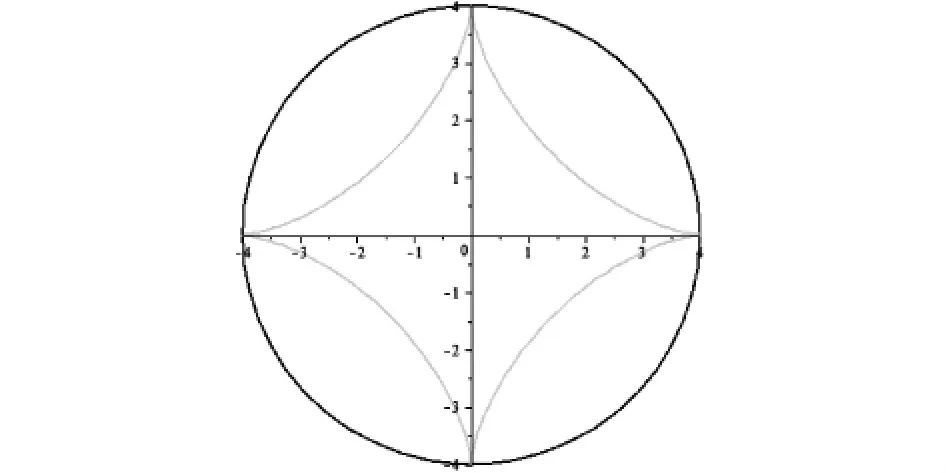
图4 R=4·r时的内旋轮线
图中绿色的曲线为星形线,蓝色的曲线是半径为4的大圆.
注 若大圆和小圆的半径是 2倍的关系,即R=2·r,此时得到的内旋轮线图形是直线,且恰好为大圆的直径.仿照上面的程序,只需要对其中的参数进行修改,很容易验证该结论的正确性.
2 Maple 软件在微分方程中的应用
微分方程是大学数学中的重要内容,很多后续课程都是以它为基础的.一般的讲解方法是在黑板上逐步推导的教学模式,如果有一步错误,那下面的推导就很难保证正确了.Maple 软件可使我们从这种繁琐的演算过程中解脱出来.通过软件,可定义微分方程;通过 DEplot命令画向量场,解释微分方程的几何意义;用 contourplot命令画积分曲线等.通过编程,可快速求解方程,并作出通解及特解图形,直观的将积分曲线的图形显示出来.通过这种方式,锻炼了学生利用数学软件解决实际问题的能力.
案例 3 求微分方程 y"-y'-y=0 的通解,满足初始条件 y|x=0=1,y'|x=0=0 的特解,并作出通解和特解的图形.
所给方程为可降阶的高阶微分方程,其特点是不显含自变量x.

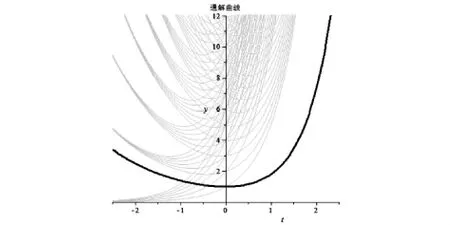
图5 方程 y"-y'-y=0 的通解和特解
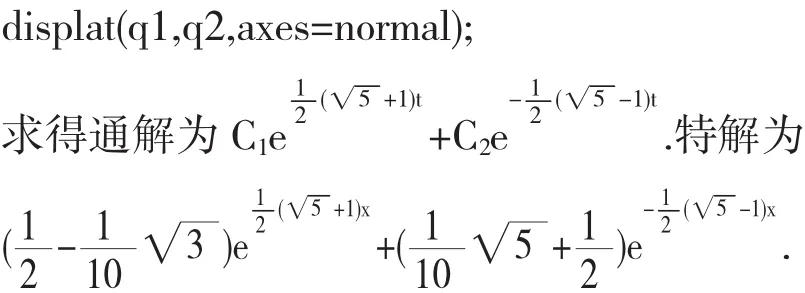
图5中绿色的曲线为部分通解;深蓝色的曲线为满足条件的特解,其显然过点(0,1),且在(0,1)处的导数为零,有水平的切线.
3 结语
大学数学的教学过程中引入 Maple 软件,可方便快速的作出平面曲线、空间曲线的图形,将抽象的数学表达式用直观的方式展现出来,便于学生深刻理解所学的知识,提高自己的认知水平.用 Maple软件支撑大学数学课程的教学,会起到事半功倍的效果,达到提高教学质量的目的,更好的适应现代化的教学,有利于学生构建数学思想、数学方法和数学技巧三位一体的数学知识体系.
〔1〕何 青 , 王 丽 芬 .Maple 教 程 [M].北 京 :科 学 出 版社,2006.
〔2〕张韵华,王新茂.符号计算系 统 Maple 教程[M].合肥:中国科学技术大学出版社,2007.
〔3〕李静,腾兴虎.Maple 软件在高等数学中的应用[J].大学数学,2014,30(Sup1):95-97.
〔4〕李 姝妹.数学 软件 Maple 在 常微 分 方 程 教 学 中的应用[J].阴山学刊,2013,27(4):55-57.
〔5〕 李 伟 .高 等 数 学 [M].北 京 :高 等 教 育 出 版 社 ,2011.
〔6〕额尔敦布和,白秀,王海清.Maple 软件在数学分析教学中的应用研究[J].内蒙古民族大学学报(自然科学版),2013,28(2):146-149.
O245
:A
:1673-260X(2016)02-0006-03
2015 年 11 月 18 日
2013 年菏泽学院重点课题组项目(201311)
