具有正系数的P-叶亚纯函数的新子类
2016-06-26杨静宇王晓英
杨静宇,王晓英
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
具有正系数的P-叶亚纯函数的新子类
杨静宇,王晓英
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
在本文中,我们利用一个由 Hadamard 卷积定义的线性算子来给出一类 P-叶亚纯函数的新子类,进一步的讨论该子类的系数不等式,偏差定理,邻域性质,等几何函数性质.得到比文献中更为广泛的结论.
Hadamard 卷积; 亚纯函数; 系数不等式; 领域
1 引言

那么称 f(z)是 α- 级亚纯星象函数.

那么称 f(z)是 α- 级亚纯凸星象函数.

定义函数 φp(a,c;z):


根据函数的 Hadamard 卷积的定义和函数 φp(a,c;z),引进线性算子 Lp(a,c)[5][6]
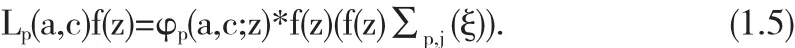


则称 f(z)∈Ls*p,j(a,c,A,B,α,m,ξ,μ,λ).
其中

那么(1.7)等价于

这就意味着存在一个柯西施瓦茨函数 w(z),使得事实上


则

2 LS*p,j(a,c,A,B,α,m;ξ,μ,λ)的 系 数 不 等 式

其中
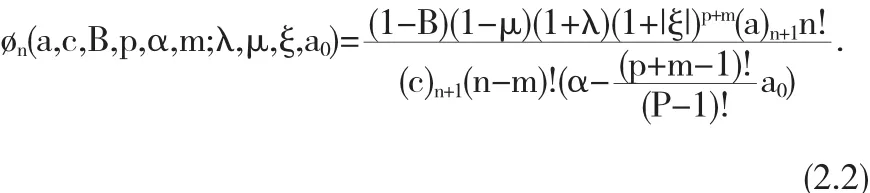


运用最大模定理,对于任意 z∈U,我们有

这意味着 f(z)∈LS*p,j(a,c,A,B,α,m;ξ,μ,λ)
相反的,假设 f(z)∈LS*p,j(a,c,A,B,α,m;ξ,μ,λ)那么我们有
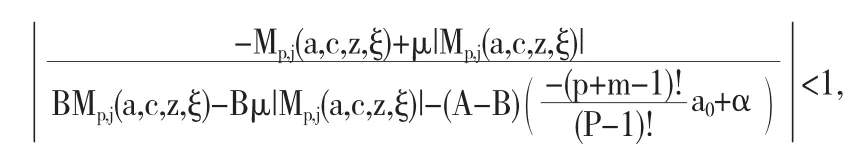
因为对于任意的 z 都有 |Rez|≤z,选择正数 z 并且使 Mp,j(a,c,z,ξ)是实数,那么我们有

取 z 为实数,并且满足 z→1-,那么我们有
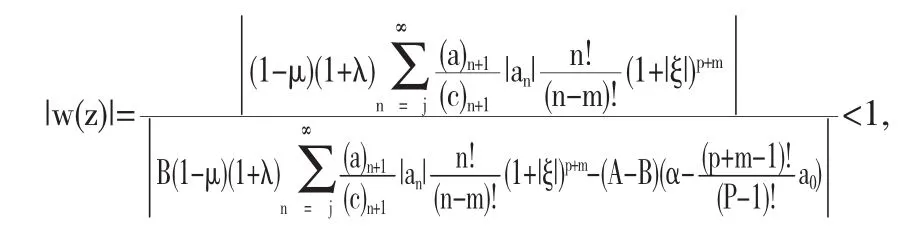
进一步我们得到
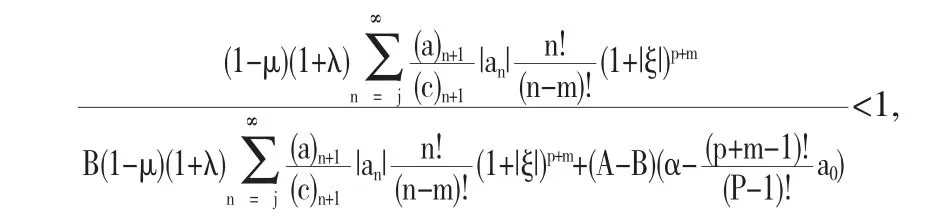
即
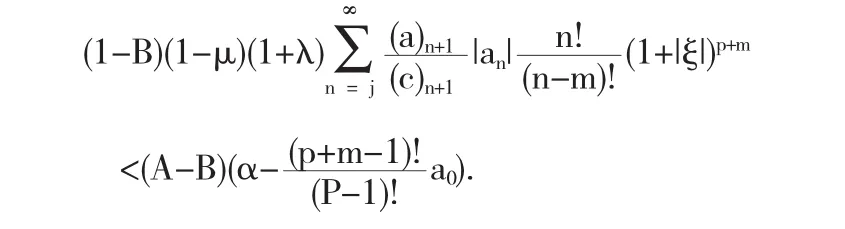
证毕.
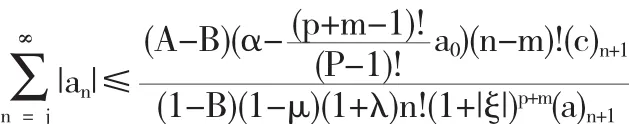
3 偏差定理

进一步的
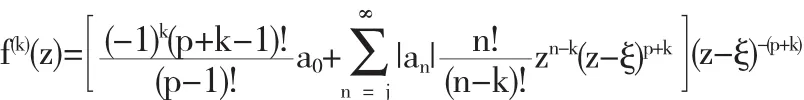
利用定理 2.1,我们可以得到(3.1).
4 LS*p,j(a,c,A,B,α,m;ξ,μ,λ)的 δ邻 域
根据 Aouf,Silverman 和 Srivastava[7]Good-man[12]和 Altintas 等早期的一些工作.我们来介绍 f(z)∈(ξ)的 δ 邻域的定义以及δ邻域相关性质.

其中

定 理 4.1 设形 如(1.1)的 函 数 属于函 数 类 LS*p,j(a+1,c, A,B,α,m;ξ,μ,λ)那么有

证 明 令 f(z)∈LS*p,j(a+1,c,A,B,α,m;ξ,μ,λ)那么根据定 理2.1,我们有

此式子等价于
进一步,对任意的
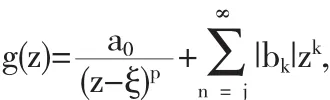
我们从(4.1)可以看出
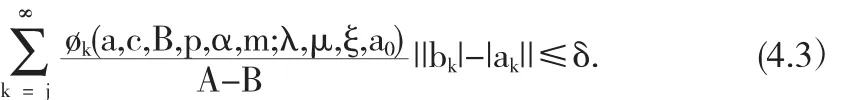
根据(4.2)和(4.3)我们得出

根据定理 2.1 得出 g(z)∈LS*p,j(a+1,c,A,B,α,m;ξ,μ,λ)

且

因为

因此 g(z)∈Nδ'+(f),
但是

根据定理 2.1 我们得出 g(z)∉LS*p,j(a,c,A,B,α,m;ξ,μ,λ).
5 改进的 Hadamard 卷积的相关性质
根据 Aouf,Silverman 和 Srivastava[7]早期的一些工作,我们讨论 LS*p,j(a,c,A,B,α,m;ξ,μ,λ) 改进的 Hadamard 卷积的性质.
对于函数

f1(z)和 f2(z)的 改 进 的 Hadamard 卷 积 用(f1·f2)表 示 且 定 义如下:
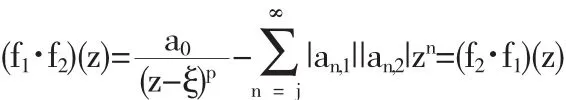
定 理 5.1 设 fk(z)(k=1,2)∈LS*p,j(a,c,A,B,α,m;ξ,μ,λ)那么
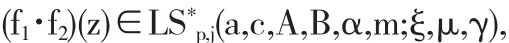
其中

当函数 fk(z)(k=1,2)被给定为下列形式时,结论成立
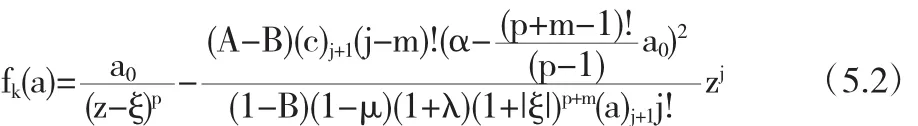
证明 根据定理 2.1,我们需要找出最小的 γ 使得
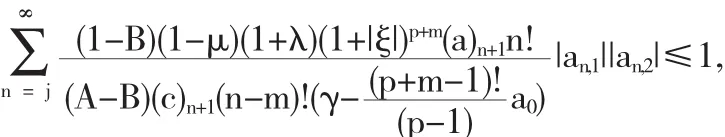
因为 fk(z)∈LS*p,j(a,c,A,B,α,m;ξ,μ,λ),那么我们有
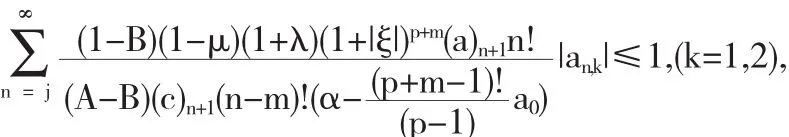
根据柯西施瓦茨不等式,进一步得到
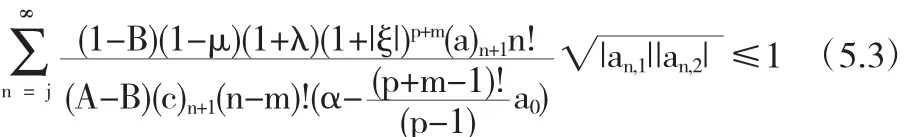
这暗示着我们仅需证明

或者是
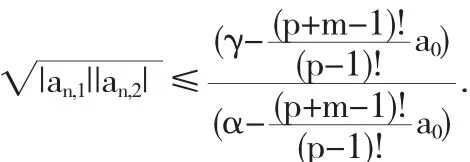
利用不等式(5.3),足以证明
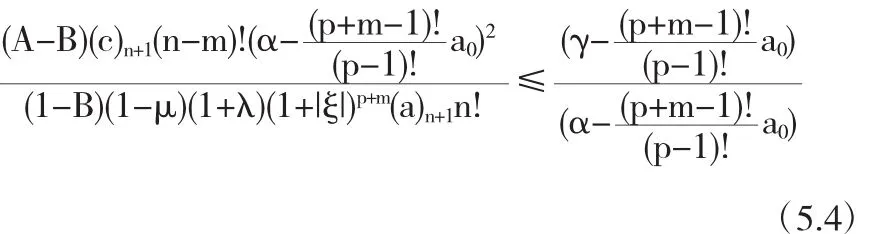
根据(5.4),我们有

定义函数 Φ(n)如下:

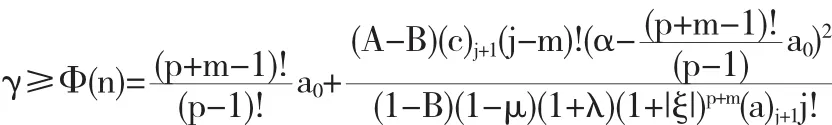
利用与定理 5.1 证明类似的方法,我们可以得到如下结论.
定 理 5.2 设 函 数 f1(z)形 如(5.1)且 属 于 LS*p,j(a,c,A,B,α, m;ξ,μ,λ),f2(z)同样形如(5.1)且于 LS*p,j(a,c,A,B,α,m;ξ,μ,λ)那么

其中
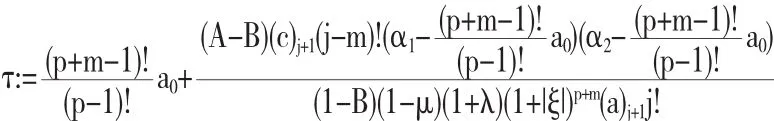
当函数 fj(z)(j=1,2)取为下列函数时,结论成立

定 理 5.3 设 fk(z)(k=1,2),形如(5.1)且属于 LS*p,j(a,c,A,B, α,m;ξ,μ,λ)定义 h(z)如下,

则 h(z)属于 LS*p,j(a,c,A,B,α,m;ξ,μ,χ)且

当函数给定为(5.2)时,结论成立.
证明 根据定理 2.1,我们要找到最小的 χ 使得

因为 fk(z)∈LS*p,j(a,c,A,B,α,m;ξ,μ,λ),(k=1,2),我们有

根据(5.6)我们有

进一步的

根据(5.7),如果我们想要证明(5.5),只要证明存在最小 χ使得

即

现在我们定义 Ψ(n):
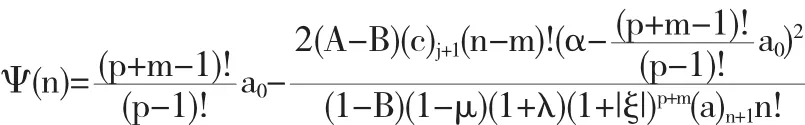
Ψ(n)关于 n 是单调递减函数.因此,因此有

证毕.
〔1〕J.E.Miller,Convex meromorphic mapping and related function,Proc.Amer.Math.Soc,25(1970),220-228.
〔2〕N.E.Cho,S.H.Lee,and S.Owa,A classofmeromorphic univalent functions with positive Coefficient,KobePJ. Math.4(1987),43-50.
〔3〕M.K.Aouf,A certain subclass of meromorphicclly starlike functionswith positive coefficient,Rend.Mat.9(1989), 225-235.
〔4〕M.K.Aouf,On a ertain subclass of meromorphicclly univalent functions with positive coefficients,Rend.Mat.11(1991),209-219.
〔5〕H.Saitoh,A linear operator and its applications of first order differentialsubordinations,Math.Japon,44(1996),31-38.
〔6〕J.-L.Liu,and H.M.Srivastava,A linear operator and associated families of meromorphically multivalent functions,J.Math.Anal.259(2001),566-581.
〔7〕M.K.Aouf,and H.Silverman,and H.M.Srivatava,Some families of linear operators associated with certa-in subclass of multivalent functions,Computers and Mathematics with Applications,55(2008),535-549.
〔8〕M.K.Aouf,and R.M.Ei-Ashwah,Properties of certain subclass ofmultivalent functions with positive coefficients,Mathematical and computer modelling.,49 (2009),868-879.
〔9〕M.K.Aouf,Certain subclass of meromorphically p-valent function with positive coefficients or negati-ve coefficients,Mathematicaland computermodelling.,47 (2008),797-1008.
〔10〕Y.G.Kim,and S.H.Lee,S.Owa,On certain meromorphically function with positive coefficients, Internat.J.Math.Math.Sci.,16(2)(1993),409-412.
〔11〕N.E.Cho, On Certain subclass of meromorphic functions with positive coefficients,J.Inst.Math.Comput. Sci.,3(2)(1990),119-125.
〔12〕A.W.Goodman,Unicalent functions and nonanalytic curves,Proc.Amer.Math.Soc.,8(1957),598-601.
〔13〕O.Altintas,and O.Ozkan, and H.M.Srivastava, Neighborhoods of a class of analytic functions with negati-ve coefficient,Appl.Math.Lett.,13(3)(2000),63-67.
〔14〕JamalM.Shenan,Application ofgeneralized fractional integraloperatorsto certain classofmultival-ent prestarlike functions with negative coefficients,Int.J.Open problems comput Math,4(2011),50-69.
〔15〕Toshio Hayami and Shigeyoshi Owa,Coefficient conditions for certain univalent functions,Int.J.open pro-blem comput.Math,1(2008),53-65.
〔16〕 李 书 海.《 特 殊 解 析 函 数 》[M].内 蒙 古 科 技 出 版 社 ,2007年 8月,第一版.
O174.5
:A
:1673-260X(2016)02-0001-05
2015 年 10 月 9 日
内蒙古自治区高等学校科学研究项目(NJZY13298)
