基于改进引力模型的中蒙俄双边贸易成本实证研究

杨瑞成，李 健

(内蒙古财经大学　金融学院，内蒙古　呼和浩特　010070)

基于改进引力模型的中蒙俄双边贸易成本实证研究

杨瑞成，李 健

(内蒙古财经大学金融学院，内蒙古呼和浩特010070)

[摘要]传统的引力模型方法在计算贸易成本时，通常认为贸易成本与地区距离和宏观经济形势相关，往往忽略了多边阻力对贸易成本的影响，而Novy(2006)在融入多边贸易壁垒对贸易成本影响的构想下提出了改进的引力模型，使得该模型更加科学合理。本文运用Novy(2006)改进的引力模型，测算了2000～2014年间中国与蒙古国、中国与俄罗斯的双边贸易成本的变化。测度结果表明，自2000年以后中国与蒙古国、俄罗斯双边贸易成本大幅下降。而在可贸易品份额为0.8，替代弹性为7时，2010年后中蒙双边贸易成本维持在0.47左右，中俄双边贸易成本维持在0.5左右。通过对比中蒙、中俄双边贸易成本，结果显示中国与蒙古国在贸易领域的相互开放程度要高于中国与俄罗斯。

[关键词]中蒙俄; 贸易成本; 改进引力模型

一、引言

近几年来,随着中国丝绸之路经济带建设同俄罗斯跨欧亚大通道、蒙古国草原之路倡议的稳步对接，为中国推进一带一路经济带建设提供了重要平台。同时，中国与一带一路沿线国家利用各自优势打造双边、多边、跨区域的贸易合作，使得中国与一带一路沿线国家贸易额呈现快速上升趋势(见图1)。图1分为两部分，上半部分为一带一路沿线国家双边贸易额占中国贸易总额的比重，下半部分为一带一路沿线国家与中国双边贸易额。根据图1可以看出2008～2015年中国与一带一路沿线国家贸易额占中国贸易比重逐年上升，而随着中国提出建设一带一路经济走廊方案，一带一路沿线国家与中国双边贸易额占中国贸易比重平均提高1.3%左右。在2014年一月达到了峰值，占中国贸易比重高达27.24%，之后逐渐趋于平稳维持在26%左右。尽管2015年中国经济面临着各种下行压力，双边贸易额呈现逐渐下降的趋势，但2015年全年一带一路对华双边贸易额占中国贸易比重平均维持在25.31%。当前，中国与一带一路沿线国家已经建设的“经济走廊”有：孟中缅印经济走廊、中蒙俄经济走廊、中国—东盟经济走廊、中巴经济走廊等。其中，由于中蒙俄三国建立并保持了长期的互利共赢的稳定的战略关系，中蒙俄之间的经济结构又具有典型的互补性特征，作为“一带一路”发展基石，“中蒙俄经济走廊”的建设具有特别意义。中蒙、中俄双边贸易快速发展不仅会拉动蒙古国和俄罗斯的经济，最重要的是，也会促进我国经济发展、加速我国产业结构升级。但是贸易成本一直是阻碍中蒙、中俄双边贸易发展的主要原因，因此，有必要对中蒙、中俄双边贸易成本进行深入研究。

图1　中国与一带一路沿线国家贸易总额资料来源：根据wind数据库提供的统计数据整理得出

在贸易成本测度方面，一般文献会采用对外依存度、资本流动等简单指标来衡量双边贸易成本，虽然这类指标测度方法简便，数据获取难度小等，但往往忽略了很多具体的因素对贸易成本的影响。在我国对贸易成本测度的认识和研究起步比较晚，具有代表性的文献有：李坤望和黄玖立(2006)利用传统引力模型测算中国自改革开放以来制造业的贸易开放度，但传统引力模型却忽略了多边阻力(Multilateral resistance)对贸易成本的影响.钱学锋和梁琦(2008)采用Novy(2006)的改进的引力模型 (revised gravity model)方法计算了1980～2006 年中国与G-7各国的双边贸易成本，结果显示，中国对外开放程度不断增强与G-7各国的贸易成本也在逐年下降，施炳展(2008)同样运用改进的引力模型计算了1980～2006年中国与世界主要经济体的双边贸易成本。许德友和梁琦(2010)运用同样的方法测度了1981～2007年中国与欧盟、美国、日本、东盟、中国香港、韩国和中国台湾的贸易成本。郑晓博,苗韧和雷家(2010)在分析OECD国家应对气候变化措施的基础上,对经典的贸易引力模型进行了扩展, 对OECD国家1991～2008年的出口面板数据进行回归, 分析应对措施中较为典型的碳税和能源效率标准对贸易竞争力的影响。

“Leamer和James Levinsohn在《The Handbook of International Economics》中认为，引力模型是计量经济学中最有使用价值的发现之一(Andrew K.R. 2002)”。进入20世纪60年代，引力模型已被应用于测算贸易成本、贸易潜力、分析贸易模式以及双边贸易流量，在国际贸易中得到广泛应用。本文将借助改进的引力模型来研究2000～2014年中蒙、中俄双边贸易成本，以及中蒙、中俄贸易优势比较。对于测度中国与一带一路沿线国家的双边贸易成本，不仅能够为中国建设中蒙俄经济走廊提供重要的科学研究价值，而且对我国和我区向北的区域经济合作也具有积极的现实意义。

二、模型概述

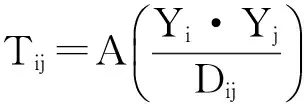
(1)

方程(1)Mijz中表示z商品从i国家出口到j国家，Yiz和Yjz表示两个国家在z商品上的花费，d代表两国之间的距离；A和a是系数，U是一个解释修正变量。随着进一步的发展在(Bergstrand.1989)中把所有的商品z加总，我们可以得到如下方程:

(2)

方程(2)为某一时期i国从j国的进口额；Yi为进口国的GDP;Yj是出口国的GDP；Dij为两国之间的距离；Uij为其它促进或阻碍两国之间贸易流动的因素。在研究国际贸易时，大多数学者都会选用引力模型，进入90年代引力模型进一步发展，为了便于回归以及构建双边贸易流量模型从而推导出修正过的引力模型。学者们将方程(2)进行改进，得到对数线性形式的引力模型：

ln(Mijt=a0+a1ln(Yit)+a2ln(Yjt)+a3ln(dij)+a4Fij)+uijt

(3)

方程(3)中ln表示自然对数，ln(A0)=a0,ln(Uijt)=uijt。Fij表示一些反映异质性的因素虚拟变量。如果存在异质性，值为1，不存在，值为0。系数a1到a3是反映的收入和距离对双边贸易流量的影响，模型(3)又可称为间接测度法。具有代表性的是McCallum(1995)用方程(3)以1988年加拿大各省市与美国各州进出口贸易数据为基础，计算加拿大各省与美国各州贸易流量。然而，任何贸易与专业化分工理论的经验研究最终都要面临贸易成本的实际测算问题，由此大量学者对其测度方法进行了大量探究。因此，引力模型在传统回归变量的基础上,加入了贸易双方的多边总体贸易成本，其主要优点在于将双边贸易量作为经济规模和相对贸易成本的函数,并且考虑了多边阻力的影响。Anderson和van Wincoop(2003)建立了Armington一般均衡框架下具有微观基础的双边贸易阻力模型分析贸易成本，由此推导出了如下形式的引力方程：

(4)

方程(4)，xij为地区i对j的出口，yw表示世界总产出，tij为t时期地区i与地区j的双边贸易出口的成本，pi·pj为价格指数，表示两地的多边阻力，∂为替代弹性。采用这种方程比较典型的文献有：Anderson和Van Wincoop (2003)用该方程和1988年美国各州的进出口贸易数据重新计算McCallum (1995)所提出的方程(3)，则发现方程(3)缺少对多边贸易阻力对贸易成本的影响。Hummels(2007)用该方程直接对二战后各国的运输成本进行了测算，并且通过距离与运输成本的关系估计了产品的替代弹性。Dennis Novy(2008)和Jacks、Meissner利用进口国的对称性，经过代数运算得到双边贸易成本变量。但是Novy(2006)指出贸易成本的变化会影响生产和消费，由于生产和消费都是外生变量，因此模型(4)的静态分析是不成立的。

三、方法测度与数据选取

(一)方法介绍

大多数学者对于贸易成本的研究一般采用间接法测度贸易成本，而本文运用Novy(2006)改进的引力模型就是典型的间接法。Novy(2006)的改进的引力模型是基于双边冰山型贸易成本的多国交易的一般均衡贸易模型。当一国出口产品到另一国，这是外生性的贸易成本就产生了，而外生性的贸易成本Samuelson (1954)又称冰山型贸易成本；该模型考虑到Krugman (1980)的垄断竞争模型；多边贸易成本壁垒的阻力；Samuelson (1954)的冰山型贸易成本，并且该模型引入可贸易品与不可贸易品。它从双边贸易模型发展到多边贸易模型。Novy(2006)推导出的引力模型形式如下：

EXPmnEXPnm=sm(GDPm-EXPm)sn(GDPn-EXPn)[(1-τmn)(1-τnm)]ρ-1

(5)

该模型在一般均衡模型的基础上，从贸易流量模型推导出两国交易的双边贸易成本。(5)式中GDPm与GDPn代表m国与n国的实际总产出，EXPmn与EXPnm代表m国向n国与n国向m国实际出口，ρ为替代弹性，sm与sn分别代表m国与n国的可贸易品的份额，τmn与τnm则代表两国间双边贸易成本。传统引力模型中，双边贸易仅由两国间距离与两国GDP决定的，这是表达不够准确，在方程(5)中τmn与τnm的双边贸易成本较高，则会导致EXPmn与EXPnm双边贸易量会下降，如果sm与sn可贸易品份额较低，则也会导致EXPmn与EXPnm双边贸易量会下降，而(5)式中的GDPm-EXPm与GDPn-EXPn是双边贸易量的重要变量，更多的学者更愿意称它为市场潜力。方程(5)是改进的引力模型，用一个简单的等式考虑了多边贸易阻力的影响。现在我们假定其他条件不变，m国对除了n国以外的其他国家的贸易成本下降，那么EXPm总出口将会增大，则m国与n国的双边贸易EXPmn与EXPnm也将下降，式中的多边阻力项EXPm与EXPn隐含了平均贸易成本。Novy(2006)模型中避免了Anderson和Van Wincoop (2003)模型中没有考虑多边贸易阻力产生的影响，因而改进的引力模型不仅包括了多边贸易成本还考虑了多边贸易壁垒。为了研究的便利，现假设双边贸易成本是对称的，即τmn=τnm,并且双边贸易份额也是相等的，即sm=sn，则将(5)式整理变形，得到方程(6)来计算双边贸易成本的公式：

(6)

由于各国出口总量变化不大，所以方程(6)中可以看出，在各国出口总量一定的条件下，两国之间的贸易成本与两国之间的贸易量和两国GDP相关，如果两国贸易量大幅度增加，则意味着两国之间贸易开放程度高，贸易成本相对较低，说明贸易量与贸易成本反相关；如果两国之间贸易没有增加，但两国GDP增加，那意味着两国之间的贸易成本增加，说明GDP与贸易成本正相关。Novy(2006)的改进的引力模型与新开放宏观经济学模型类似，改善了传统引力模型测度双边贸易仅由两国间距离与两国GDP决定的，而且改进的引力模型在数据获得性比较容易，因此本文运用Novy(2006)的引力模型来测度中蒙俄三国双边贸易成本。

(二)数据选取

本文将利用改进的引力模型方程(4)对中蒙、中俄双边贸易成本进行测度，鉴于一带一路的中蒙俄经济走廊于2014年提出，并且考虑到数据的可获得性和蒙古国、俄罗斯数据已更新至2014年，因此，我们将选择样本年限定在2000～2014年，其能基本反映中国对蒙古国、俄罗斯的贸易情况。现在我们需要获取中国与蒙古国、俄罗斯各自国家的出口总额、中蒙与中俄的相互的出口数据以及三国的实际GDP。我们将通过http://comtrade.un.org/的联合国商品贸易统计(UK comtrade)数据库来获取中蒙、中俄的名义出口数据，而Wind的宏观经济数据库提供了世界主要国家的出口数据、实际GDP数据、出口价格指数等等指标，因此，我们也将通过Wind数据库来获取中国、蒙古国、俄罗斯三个国家2000～2014年的出口数据和实际GDP数据。但是考虑到国家间汇率变化和价格波动的差异对研究的影响。我们将借鉴钱学锋和梁琦(2008)运用改进的引力模型测度中国与G7国家双边贸易成本与许德友和梁琦(2010)运用同样方法测度1981～2007年中国与主要贸易伙伴的双边贸易成本中对数据的进行平减处理，以此来消除价格波动与汇率差异对数据的影响，我们也将采用同样的方法对数据进行平减处理，并统一采用2007年美元价格计算，从而得到处理后的中蒙俄三国处理后的数据。

方程(6)中可以看出还有两个参数s和ρ，即可贸易品份额和替代弹性还需要我们设定。而其中参数s在其他条件不变时，当s越小时贸易成本也就越低，由于s参数很难直接计算得出，我们将参考已有的文献。Novy(2006,2007)和Jacks(2006)将s定为0.8,同样国内学者也都将s定为0.8，并且Evenett和Keller(2002)在考察可贸易品时认为,可贸易品数值大概界定在0.3～0.8，因此，本文也将遵从国内外学者的研究成果将可贸易品份额s界定在0.8。但替代弹性ρ也是很难计算得出，国外学者Anderson和van Wincoop(2004)通过对原有文献整理并重新计算认为替代弹性ρ一般界定在5～10之间，在国内学者钱学锋和梁琦(2008)与许德友和梁琦(2010)都将替代弹性ρ设为 5(低弹性)与10(高弹性), 并且都较好的反映了中国双边贸易成本的变化。而Novy(2006)的研究中将弹性ρ设定为11与8来考察1960～2002年间美国与加拿大的贸易成本。本文为了更好的考察中蒙与中俄双边贸易成本，且区间范围过大，所以本文再选取一个替代弹性的中间值，故将弹性设定为三个档次：5(低弹性)、7(中弹性)以及10(高弹性)来观察每个弹性档次双边贸易成本的变化。

四、实证研究分析

(一)实证数据结果

我们借助Novy(2006)的改进引力模型，计算了2000～2014年间中国与蒙古国、俄罗斯的双边贸易成本的变化，表1中给出了当可贸易品份额s=0.8时，低、中、高三个档次的弹性指数下2000～2014年间中蒙、中俄双边贸易成本。

从表1可以看出三种不同弹性下中蒙、中俄双边贸易成本，可以看出随着中蒙、中俄经济的发展与贸易联系更加紧密，使得2000～2014年间中蒙、中俄双边贸易成本呈现逐渐下降的趋势。当弹性为ρ=5时，中蒙贸易成本变化维持在：0.59～0.71之间、中俄贸易成本维持在0.64～0.69之间；当弹性为ρ=10时，中蒙贸易成本变化维持在：0.33～0.42之间、中俄贸易成本维持在0.37～0.40之间。本文以弹性ρ=7为详细说明2000～2014年间中蒙、中俄双边贸易成本的变化，从表1中ρ=7这一列可以看出，2010年中蒙两国经济逐渐上升与双方贸易往来更加紧密，使得中蒙双边贸易成本从最初的0.54下降到0.47左右，经过2009年金融危机影响后，中蒙双边贸易成本平均维持在0.47左右。反观中俄双边贸易成本可以从表1中看出中俄双边贸易成本变化不均匀，主要由于中俄可贸易份额较大，双边贸易成本基本维持在0.5左右，但由于2009年俄罗斯经济大滑坡，全年GDP同比下降7.8%，导致双边贸易成本接近0.54，2011年之后随着俄罗斯经济复苏，双边贸易成本逐渐下降，2013年俄罗斯经济形势有所低迷，可以看出中俄贸易成本较2012年有所增加。这与Novy(2006)指出“两国之间的贸易成本与双方经济形势与贸易往来程度有关”的观点相一致。

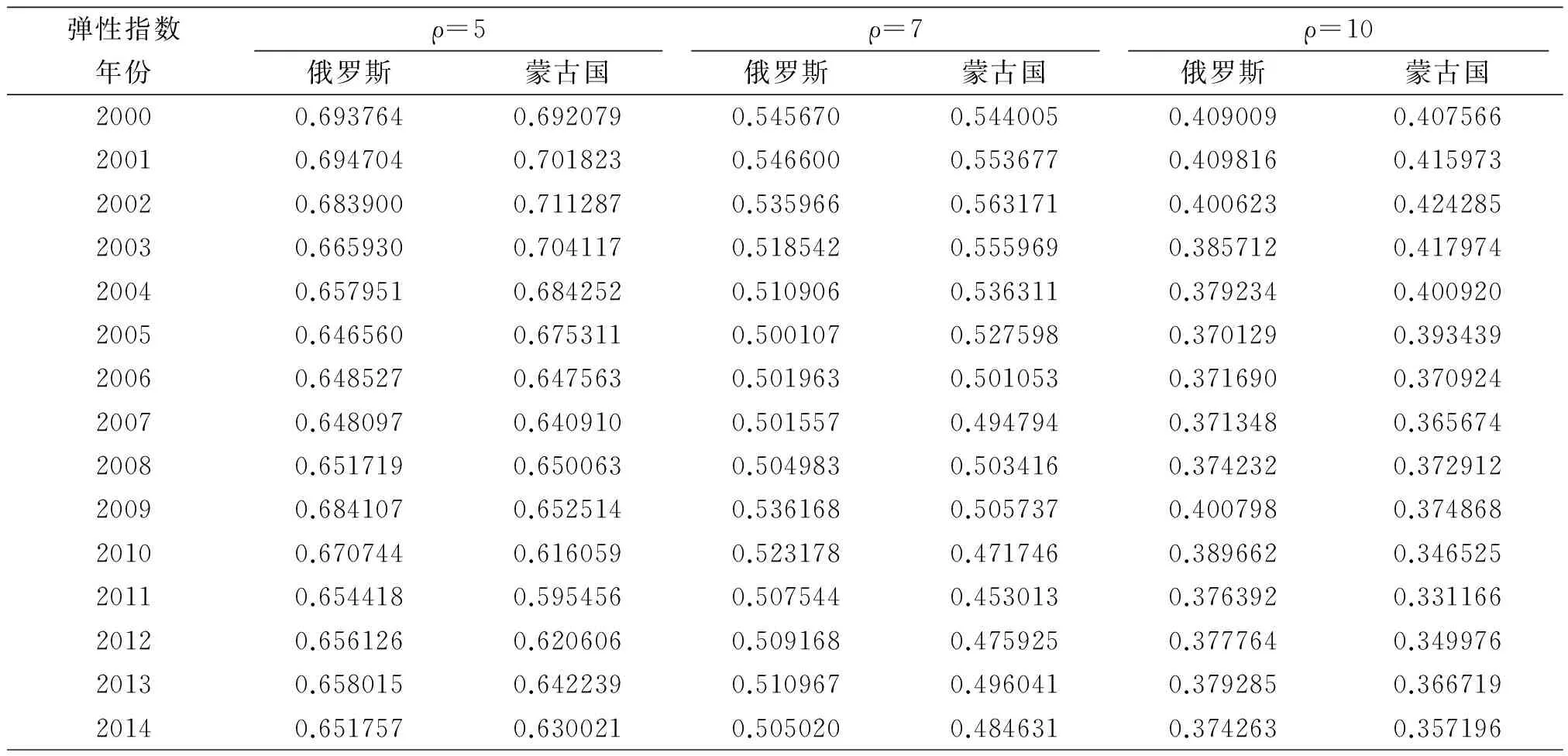
表1　中国与蒙古国、中国与俄罗斯双边贸易成本(s=0.8)

(二)中蒙、中俄双边贸易对比

为了更能清晰的观察中蒙、中俄双边贸易成本的变化，本文给出中蒙与中俄不同替代弹性下贸易成本变化的综合图2。从图2可以明显看出，2000～2007年间，中蒙、中俄双边贸易成本逐年下降，而中俄双边贸易成本下降幅度大于中蒙双边贸易成本下降幅度。在2007年时中蒙、中俄双边贸易成本基本相等。自2008～2009年美国爆发次贷危机，影响全球经济形势，导致中蒙、中俄双边贸易成本增大，2010～2014年全球经济有所复苏，中俄双边贸易成本都呈现平缓下降趋势，但中蒙双边贸易成本波动幅度较大，虽然中蒙两国GDP增速都有所增加，但中蒙两国双边贸易量变化不大，这与方程(6)中“如果两国GDP增加，但没有带来两国贸易的增加，那意味着两国之间的贸易成本上升”的解释相一致。

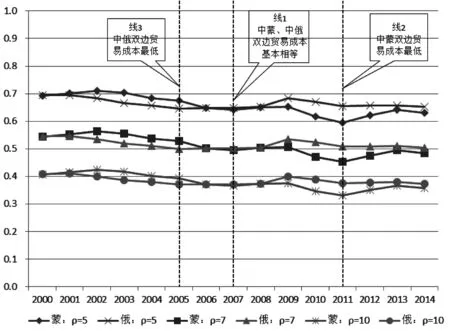
图2　双边贸易成本变化(ρ=5、ρ=7、ρ=10)

现在为了更好观察不同替代弹性时中蒙、中蒙贸易成本大小与变化情况，我们给出不同弹性下中蒙双边贸易成本变化图3与中俄双边贸易成本变化图4。通过图3与图4可以看出不同替代弹性对双边贸易成本影响较大，例如：2014年中蒙双边贸易成本在ρ=5时约为0.63，而在ρ=10时双边贸易成本约等于0.36，这说明替代弹性ρ越高时双边贸易成本越小，反之，替代弹性ρ越低双边贸易成本越高，所以双边贸易成本与替代弹性ρ反相关。从图2与图3可以看出尽管替代弹性不同，但双边贸易成本的变化趋势仍然是相同的，我们的结论与Novy(2006)所指出的贸易成本的变化与替代弹性无关的结论相一致。通过图2与图3对比可以发现中俄双边贸易成本变化趋势较为平缓，而中蒙双边贸易成本变化趋势波动幅度较大。我们给出中俄与中蒙在不同弹性下双边贸易变化的标准差，以便更好说明变动趋势。当ρ=5时：中蒙贸易成本标准差为0.035486，中俄贸易成本标准差为0.016901；当ρ=7时：中蒙贸易成本标准差为0.033880，中俄贸易成本标准差为0.016317；当ρ=10时：中蒙贸易成本标准差为0.028713，中俄贸易成本标准差为0.013925。从不同弹性下标准差的结果可以看出，中俄贸易成本标准差始终小于中蒙贸易成本标准差，说明中俄贸易成本较稳定，这也更好解释了图2与图3变化趋势。此外，通过图2与图3我们会发现中蒙贸易成本始终低于中俄贸易成本，说明中国与蒙古国之间市场开放程度比中国与俄罗斯市场开放程度高，可能由于中国与俄罗斯之间仍然存在“灰色清关”等贸易障碍，影响俄罗斯对中国的出口。

图3　中国与蒙古国贸易成本　　　　　　　　图4　中国与俄罗斯贸易成本

五、结论与建议

本文采用Novy(2006)改进引力模型，并结合2000～2014年相关数据测算了中蒙、中俄双边贸易成本。结果显示：2000～2014年中蒙、中俄双边贸易成本都呈现下降趋势，其中中蒙双边贸易成本波动幅度较大，可能由于蒙古国GDP不稳定波动幅度较大而出口总额基本没有变化，而中俄双边贸易成本波动较小，主要由于俄罗斯经济较为稳定，对中国出口总额也比较稳定。中蒙、中俄双边贸易成本的下降也反映了我国对蒙古国、俄罗斯贸易自由化程度不断加深，贸易壁垒逐渐下降，说明中蒙俄经济走廊提出是我国经济发展与蒙古国、俄罗斯经济共同繁荣的契机也为各国产业和服务贸易提速升级提供了机遇，这也是本文研究中蒙、中俄双边贸易的意义所在。

本文受到各种因素的制约还存在不足之处：一是受到数据的可获得性的制约，本文没能对其他经济走廊一一分析贸易成本，对比中蒙俄经济走廊与其它经济走廊的贸易成本，观察我国所提出的经济走廊哪些具有明显优势。二是笔者认为Novy(2006)模型忽略了双边政治、人口变化等因素对贸易成本的影响，两国的制度环境和宏观经济政策导向可能会对双边贸易成本产生影响。这些问题笔者将在后续研究中逐渐解决。

[参考文献]

[1]杜凤莲,赵鹏迪.中蒙、中俄贸易互补性及其潜力分析[J].广播电视大学学报(哲学社科版),2012,(01).

[2]李坤望,黄玖立,施炳展.中国与主要贸易伙伴的双边贸易自由度——基于新经济地理学的一个衡[J].世界经济文汇,2006,(04).

[3]钱学锋,梁琦.测度中国与G7的双边贸易成本——一个改进引力模型方法的应用[J].数量经济技术经济研究，2008,(02).

[4]施炳展.我国与主要贸易伙伴的贸易成本测定——基于改进的引力模型[J].国际贸易问题，2008,(1).

[5]许德友，梁琦.中国对外双边贸易成本的测度与分析：1981-2007年[J].数量经济技术经济研究，2010,(01).

[6]郑晓博,苗韧,雷家.应对气候变化措施对贸易竞争力影响的研究[J].中国人口·资源与环境，2010,20(11)：66-71.

[7]Tinbergen J.Shapingthe World Economy:Suggestions for an International Economic Policy[M].New York: The Twentieth Century Fund,1962.

[8]Poyhonen,P.A Tentative Model of the volume of Trade between Countries[J].Weltwirtschaftliches Archiv,1963,(90):93-99.

[9]Bergstrand,J.H.The Generalized Gravity Equation, Monopolistic Competition and the Factor Proportions Theory in International Trade[J].The Review of Economics Statistics,1989,(71):143-153.

[10]McCallum,J.National Borders Matter,Canada-U.S. Regional Trade Patterns[J].Atlantic Economic Journal,2003,(2):174-187.

[11]Anderson,J.Eand van Wincoop,E.,Borders, Trade and Welfare[C].BrookingsTrade Forum 2001,Susan Collins and DaniRodrik,eds.,Washington:The Brookings Institution,2002:207-244.

[12]Anderson,J.Eand van Wincoop,E.,Gravity with Gravitas :A Solution to the Border Puzzle[J].American Economic Review,2003,(93):170-192.

[13]Jacks,D.S.,Meissner,C.M.andNovy,D.Trade Costs in the First Wave of Globalization[R].NBER WorkingPaper,No.12602.

[14]Hummels,D.Toward a Geography of Trade Costs[R].Purdue University,2001,(9).

[15]Novy,D.Is the Iceberg Melting Less Quickly? International Trade Costs after World War II[J].Mimeo University of Warwick,2006,(02).

[16]Jacks,D.S.Meissner,C.M.and Novy,D.Trade Costs in the First Wave of Globalization[R].NBER Working Paper,2006,No.12602.

[17]Novy,D.,Is the Iceberg Melting Less Quickly? International Trade Costs after WorldWar II[Z].Working Paper,Mimeo,University ofWarwick,2006.

[18]Fujita,M,P.Krugman,and A.Venables,The Spatial Economy:Cities,RegionsandInternational Trade[M].Cambridge,MA:MIT Press,1999.

[责任编辑：安锦]

The Empirical Research of Bilateral Trade Costs among China,Mongolia and Russia Based on the Improved Gravity Model

YANG Rui-cheng,LI Jian

(Shool of Finance, Inner Mongolia University of Finance and Economics, Hohhot 010070, China)

Abstract:For computing trade costs, the traditional Gravity model considered the macroeconomic situation and related areas distance, and often overlooked the multilateral resistance of trade costs. By absorb integration into the multilateral trade barriers on costs, Novy(2006) put forward an modified gravity model, and made the model more scientific and reasonable. This paper used the Novy modified gravity model to estimate the change in the cost of bilateral trade between China and Mongolia, China and Russia from 2000 to 2014. Empirical results showed that China and Mongolia, the Russian trade costs had declined effectively since 2000. When the tradable goods share was 0.8 and the elasticity of substitution was 7, the trade costs between China and Mongolia was around 0.47 after 2010, while the bilateral trade costs between Russia and Mongolia remained around 0.5. By contrasting bilateral trade costs between China and Mongolia, China and Russia, this paper showed the mutual openness between China and Mongolia in the field of trade than China and Russia.

Key words:China, Mongolia and Russia; trade costs; improved Gravity Model

[收稿日期]2016-03-03

[基金项目]国家自然科学基金资助项目(71261015)；国家社会科学基金资助项目(15XMZ081)；内蒙古自治区高等学校创新团队发展计划支持(NMGIT1405)；内蒙古草原英才工程及高等学校青年科技英才支持计划

[作者简介]杨瑞成(1970-),男,山东潍坊人，内蒙古财经大学金融学院教授，博士，博士后，从事金融工程研究.

[中图分类号]F752

[文献标识码]A

[文章编号]2095-5863(2016)03-0038-07