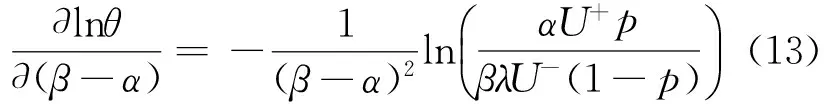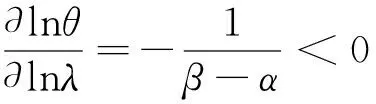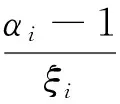基于资产配置的损失厌恶效用参数研究①
2016-06-24张小涛李悦雷
张小涛, 潘 琪, 李悦雷
(1. 天津大学管理与经济学部, 天津 300072; 2. 天津市复杂管理系统重点实验室, 天津 300072)
基于资产配置的损失厌恶效用参数研究①
张小涛1,2, 潘琪1, 李悦雷1,2
(1. 天津大学管理与经济学部, 天津 300072; 2. 天津市复杂管理系统重点实验室, 天津 300072)
摘要:利用单期经济环境中具有损失厌恶效用的投资者的资产配置问题分析了Kahneman和Tversky提出的前景理论中损失厌恶效用的曲率参数和损失厌恶系数的取值范围及其之间的关系,得出两个曲率参数α, β不相等,且β大于α;同时发现损失厌恶系数λ的下界不是固定不变的,而是随着市场环境的变化而改变;投资于风险资产的比例是曲率参数β, α之差的函数,并随着β-α增加而增加.本文使用中国股票市场的收益数据对理论分析进行了实证检验,实证结果与理论分析结果基本一致,并发现中国市场下的损失厌恶系数下界远小于英美等发达国家市场.
关键词:资产配置; 损失厌恶效用; 损失厌恶参数
0引言
人们做各种决策的时候都会面临未来相对于当前状态有损失或收益的可能性,此时通常人们会表现出明显的风险偏好差异.比如大部分人会拒绝参加有一半胜负比率的赌博,除非获利能达到损失的两倍左右[1].前景理论(prospect theory)使用损失厌恶(loss aversion)的概念解释了这种混合赌博中的风险厌恶现象[2]:即人们面对相同数量损失或获利的可能时,对损失更敏感[3].损失厌恶解释了许多经济行为,比如股权溢价之谜[4]、消费者品牌选择异象等[5],在中国市场上,股票市场的波动不对称现象也可以用损失厌恶进行很好的解释[6],损失厌恶也可以很好地解释个体“好消息提前”的行为,却不能解释“坏消息延后”的现象[7].损失厌恶现象不但广泛存在于经济社会中,而且在5岁幼童和卷尾猴的交易行为中也发现了普遍的损失厌恶现象[8],Chen等[9]认为这表明损失厌恶反映了灵长类动物对不确定评价的基本特征,Tom等[10]更进一步通过对人脑的神经学实验研究证实了损失厌恶产生的神经学基础.以上的研究表明损失厌恶不但会出现在人的经济决策中,最近的神经学研究更证明了损失厌恶存在的生理学基础及其存在的普遍性.
与标准的幂效用函数不同,损失厌恶幂效用包括了3个参数(α、β和λ):α和β是解释效用对获利和损失敏感性的曲率参数,λ是度量损失相对获利的效用的损失厌恶系数.这3个参数的不同取值及其组合可以刻画投资者对风险、获利和损失的不同态度.Kahneman和Tversky[2]建议α和β取0.88,λ取2.25,并被多数研究者采用,比如Benartzi 和Thaler[4],Berkelaar等[11],Barberis和Huang[12], Ang等[13]在他们的研究中使用了类似的参数值.但是,有些研究,比如Camerer和Ho[14]与Wu和Gonzalez[15]虽然认为两个曲率参数应该是相同的,但是要比Thaler等[16]估计的要小.同样,Patricia[17]在研究损失厌恶对贸易政策影响时,使用非线性回归方法得到损失厌恶系数大约为2,与Kahneman和Tversky的实验结果相近,但也要小一些.更进一步,Booij等[18]通过对1 935个具有代表性的公众进行分析,研究了正收益与负收益情况下的效用函数和概率权重函数,发现损失厌恶系数约为1.6,这个数值与Kahneman和Tversky[2]估计的2.25要小很多.Hwang和Satchell[19]发现不同国家市场上的损失厌恶参数是不同的,美国和英国市场上的损失厌恶系数分别是3.25和2.75,并随着市场环境的变化而改变.与此同时,不同的损失厌恶程度会影响人的决策行为,比如较高的损失厌恶导致投资于风险资本市场的概率减少,配置于风险资产的比例也较低[20],具有损失厌恶特征的报童的订单量高于风险中性的报童的订单量[21],在证券市场上,损失厌恶系数与市场状态和投资者风险偏好相关,尤其是在中国市场背景下研究投资者的损失厌恶效用采用Kahneman 和 Tversky[2]提出的参数值是不合适的[22].
综上可知,国内外研究者对损失厌恶幂效用参数的取值持有不同观点,损失厌恶各参数的取值并不统一,其取值会随着国家地区以及市场环境的变化而变化.因此使用前景理论进行研究和决策时,如果不能确定合理的各参数,由此得出的决策结果是值得商榷的.因此如何准确测定损失厌恶参数是十分必要的工作,Wakker和Deneffe[23]设计的权衡法(trade-off)可以分别度量获利和损失的效用, Abdellaoui等[24]则设计了不用事先对参数进行任何假设的,可以同时测量获利和损失效用的无参数度量损失厌恶的实验方法,而国内学者在损失厌恶参数测度方面的研究极少.国内的研究者将损失厌恶理论应用到了经济、金融、供应链等诸多领域,并多沿用Kahneman和Tversky[2]基于美国大学生实验提出的参数,但是已有研究表明不同国家和市场的决策者损失厌恶参数是不同的,而且受试者在实验室无法完全模拟真实的决策环境,在实验中有许多重要因素不方便或没有办法考虑进去,比如资产收益的真实概率分布或者是涉及大额损益时的决策行为.因此,本文通过设定一个单期经济环境的资产配置模型,研究损失厌恶效用的各个参数,并利用中国证券市场的交易数据估算出中国投资者的损失厌恶参数范围.
1资产配置下的损失厌恶效用参数
1.1模型设定
为了便于分析,令下面的方程为幂效用损失厌恶函数
(1)
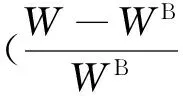
假定只存在两类资产:无风险资产和有风险的证券资产,其收益分别用rf,rp表示.θ表示持有风险资产的比例,那么最终财富可以写为
W=W0(1-θ)(1+rf)+W0θ(1+rp)
=WB+θW0re
(2)
其中WB=W0(1+rf)为投资于无风险资产得到的收益;re=rp-rf为风险资产的超额收益.因此损益用θW0re表示,资产配置问题就是寻找使损失厌恶效用函数U(θW0re)最大的θ.
1.2KST分布及损失厌恶效用中曲率参数α和
β的关系
最优投资组合可以通过适当的选择θ得到.令

U-=E((-re)β|re<0),
p=prob(re>0)
其中期望使用的是主观概率密度函数.
Knight等[25]设计了可以刻画资产收益不对称现象的分布函数(以下简称KST分布),KST分布的密度函数为Scale Gamma分布,该分布在计算期望效用时简便易行,因此本文在后面的模型推导和实证分析中,将使用KST分布来计算超额收益(具体分析参见2.2节参数估计部分).在此使用xt表示t时刻风险资产的超额收益,那么就可以写出正的超额收益xt的概率密度函数为

(3.1)
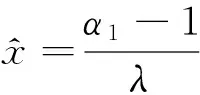
同理,对负的超额收益xt的概率密度函数为
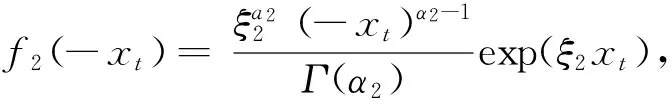
(3.2)
有类似于式(3.1)的结论.
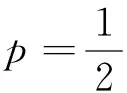
另外为讨论方便起见,本文中总是假设0≤θ≤1,即股票市场不允许卖空.
结合前面对U+,U-的定义可知
U+=E(xa|x>0)
(4)
类似地可以得到U-,综合上述推导可以得到
(5)
由于方程(1)的X等价于θW0re,因此期望损失厌恶效用ULA可以由下式给出
ULA=(θW0)αpU+-λ(θW0)β(1-p)U-
(6)
从方程(6)的最大化一阶条件可知
(7)
首先考虑α=β的情况.此时一阶导数变为

当U+p-λU-(1-p)>0时,ULA单调递增,θ越大效用越大;当U+p-λU-(1-p)<0时,ULA单调递减,θ=0时效用最大;当U+p-λU-(1-p)=0时,ULA是常数,效用不随θ的改变而改变.
第1种情况下,投资者会将资产全部配置于风险资产;第2种情况下,投资者会将全部资产全部配置于无风险资产;第3种情况下,投资者的资产配置与效用无关.很显然当α=β时,资产配置或者出现极端情形或者违反效用准则,由此可以知道,获利和损失时的幂效用参数不应该相等,与Kahneman和Tversky[2]给出的建议不同.
下面考虑当α≠β时的情形,此时求解式(7)可得
(9)
取对数后,可以写为
(10)
<0
(11)
把上面的公式重新整理得
(12)
上式中的变量均为正值,且α-1,β-1,1-p各项也均大于零.
结合方程(9)中的一阶条件可以得出α,β应满足β-α>0,因此,方程(6)中最大化预期损失厌恶效用存在最优解的充要条件是必须同时满足式(9)和式(12).方程(9)显示的是在给定的损失厌恶参数值下风险资产投资的比例.在投资者行为模式没有改变的假设下,也就是损失厌恶参数不随时间改变的前提下,投资于风险资产的比例是U+和U-以及p的非线性函数.α,β之间的关系将会在后文中进行具体的讨论.
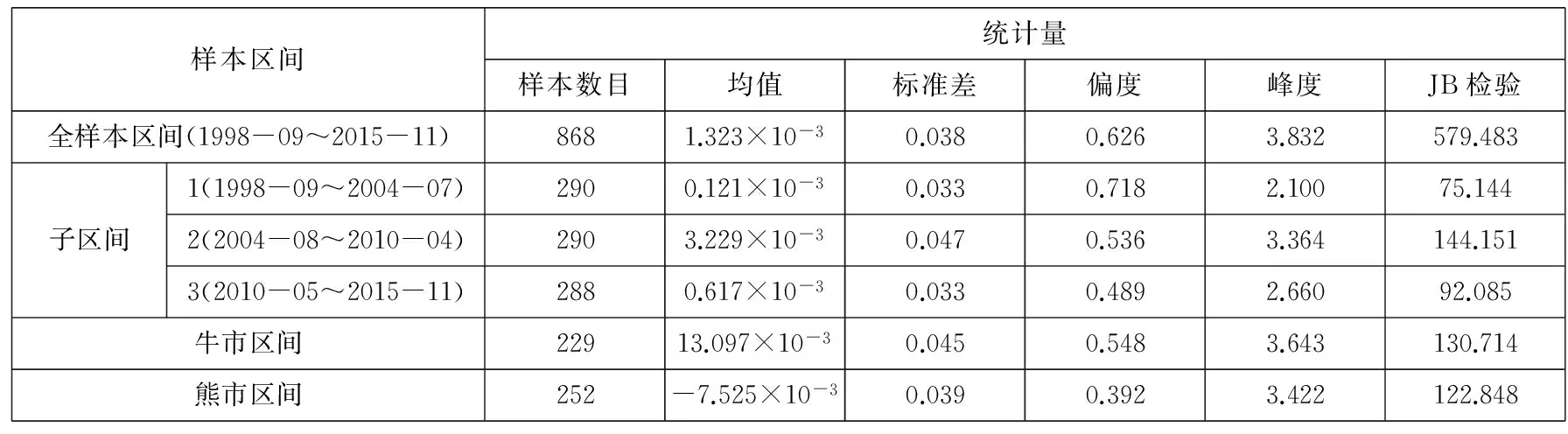
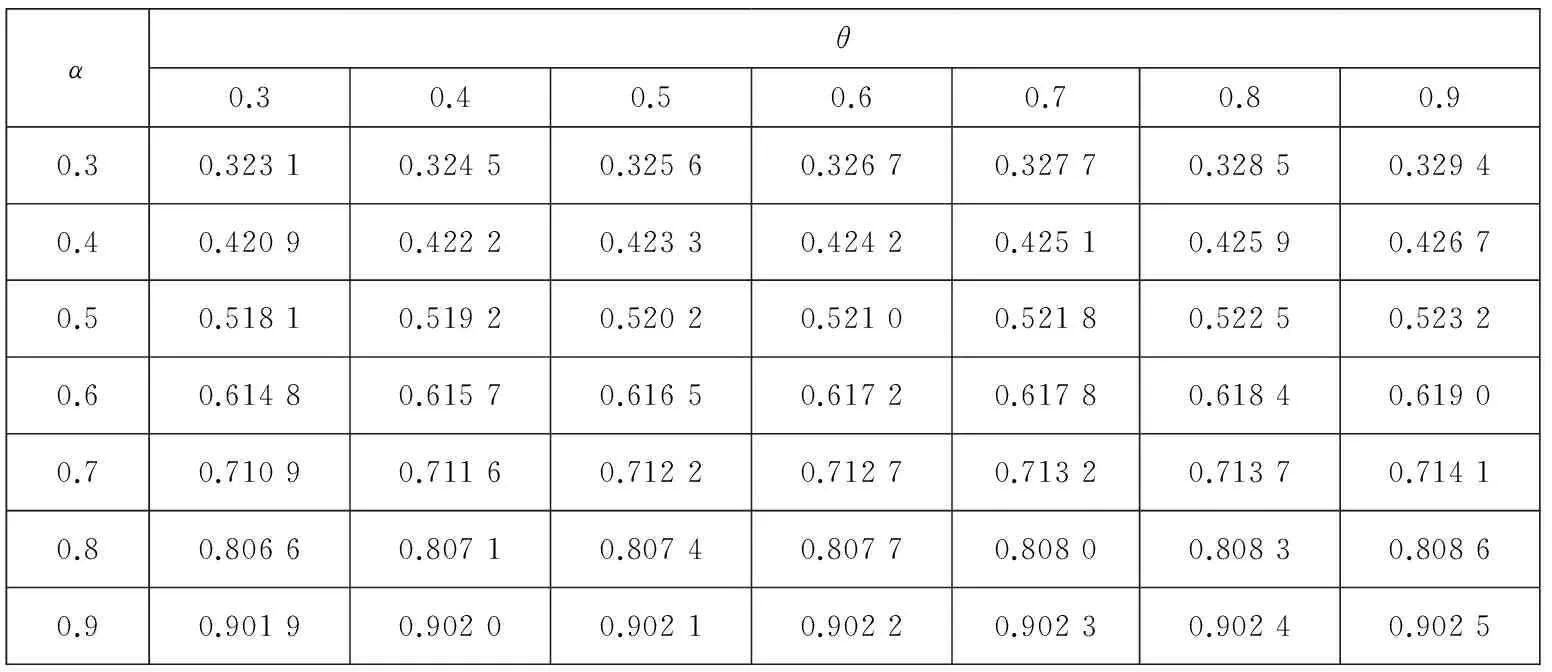
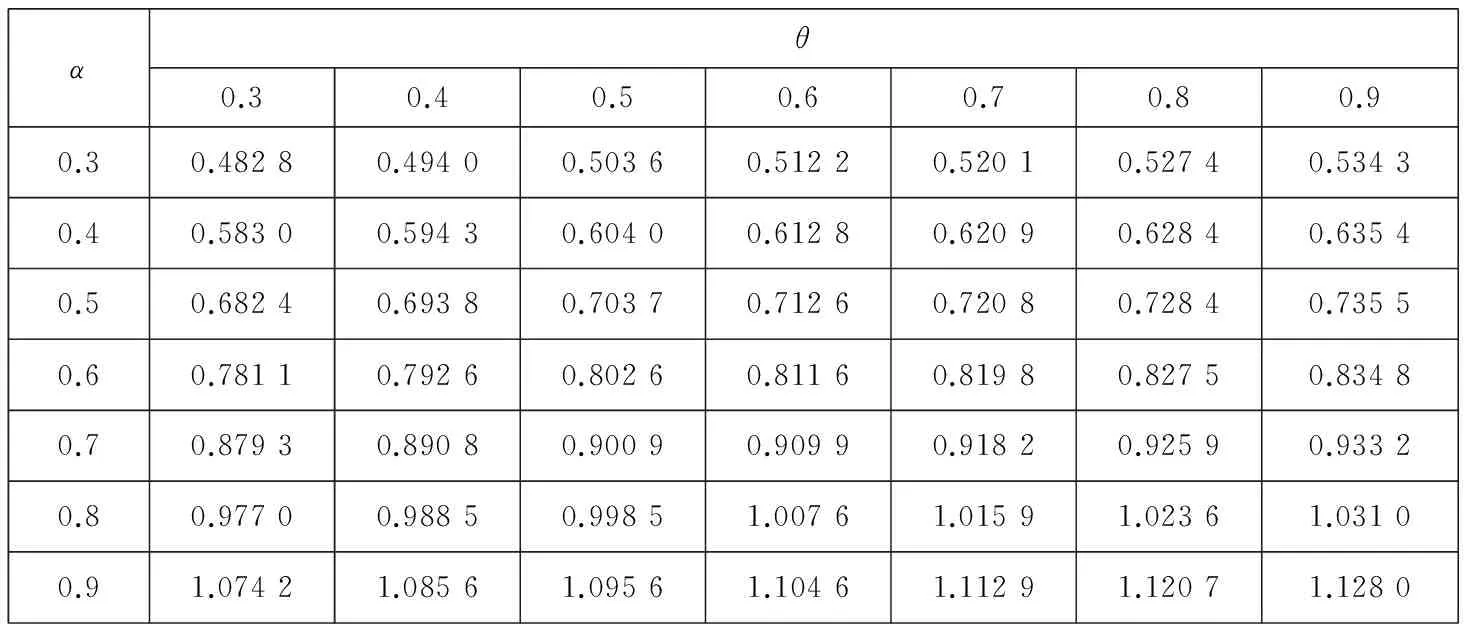
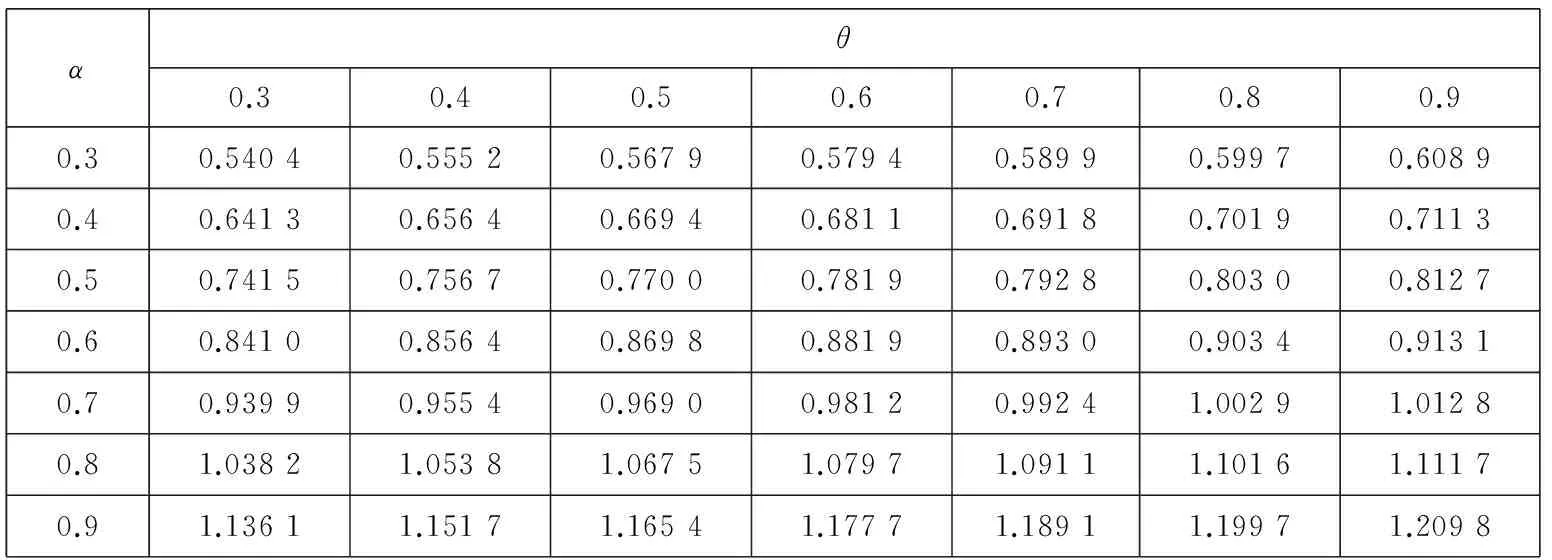
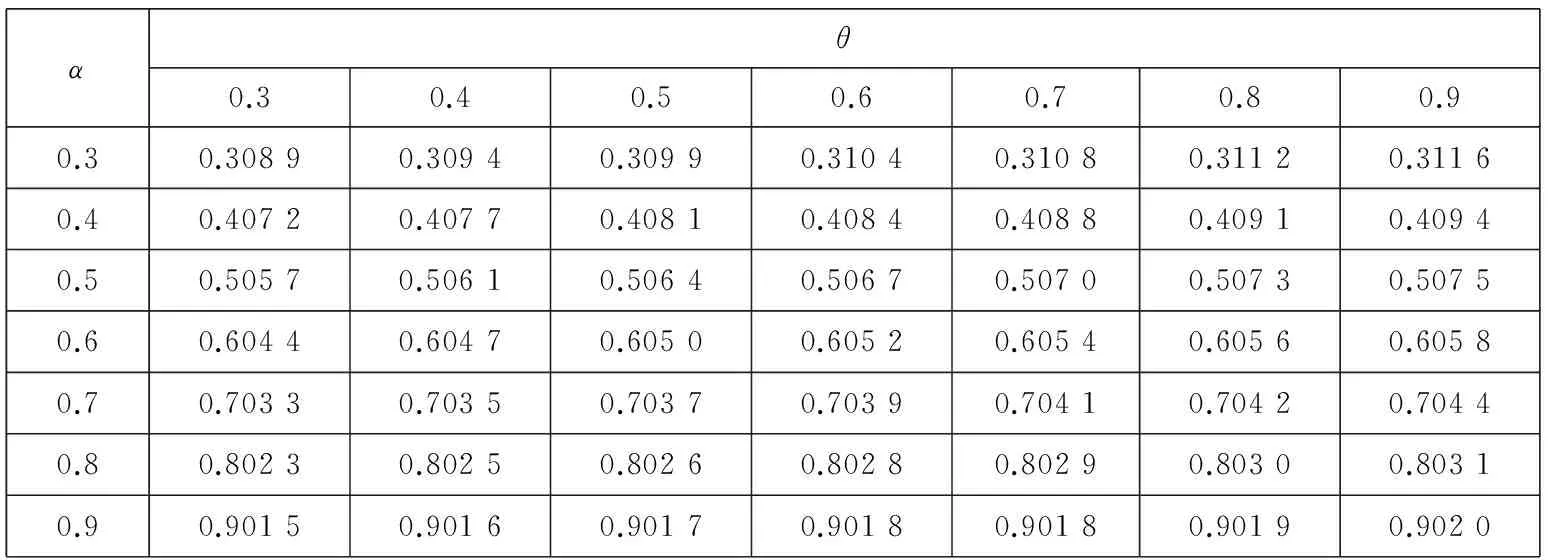
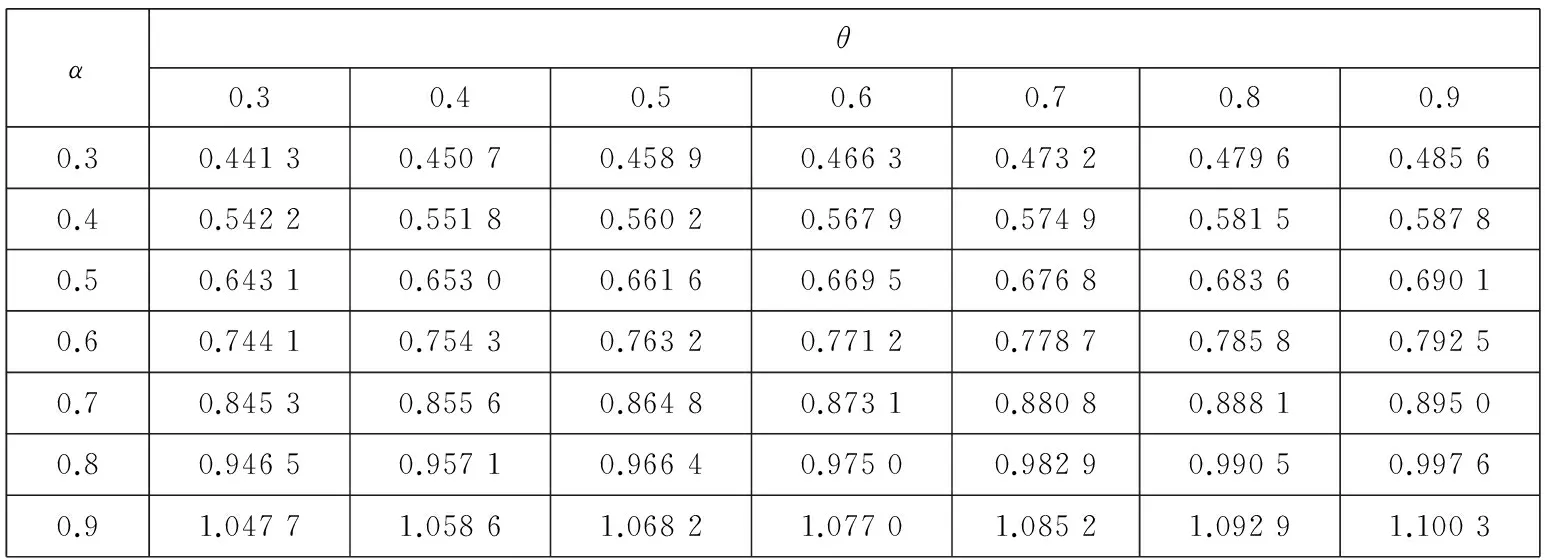
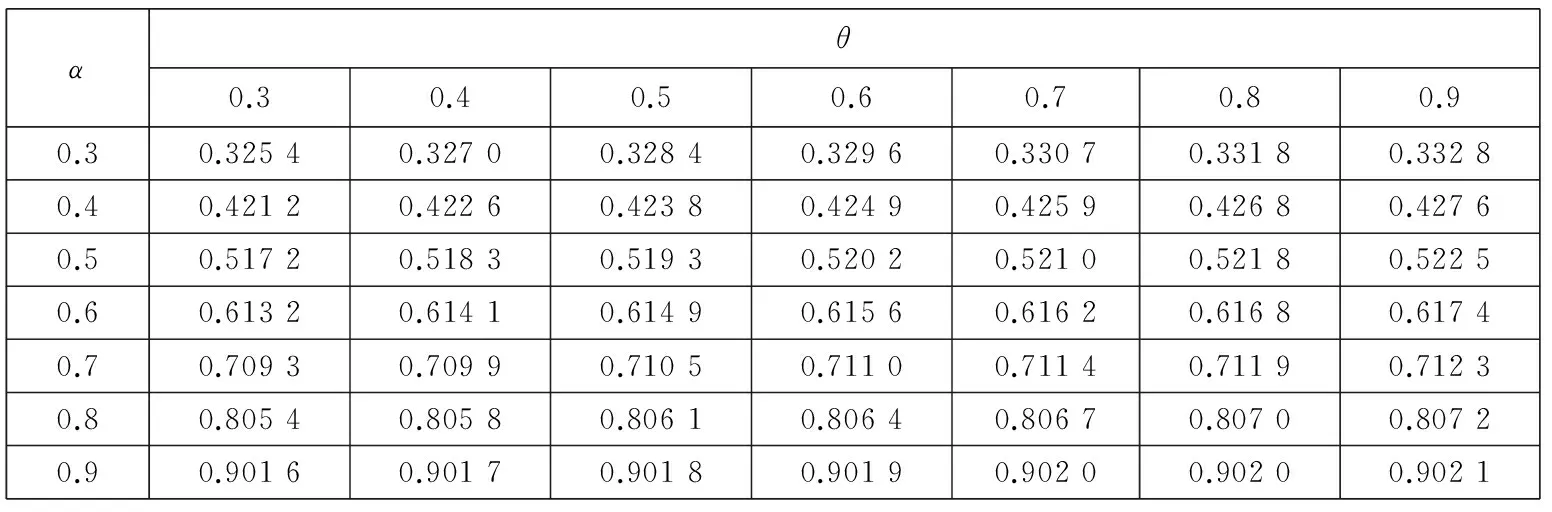
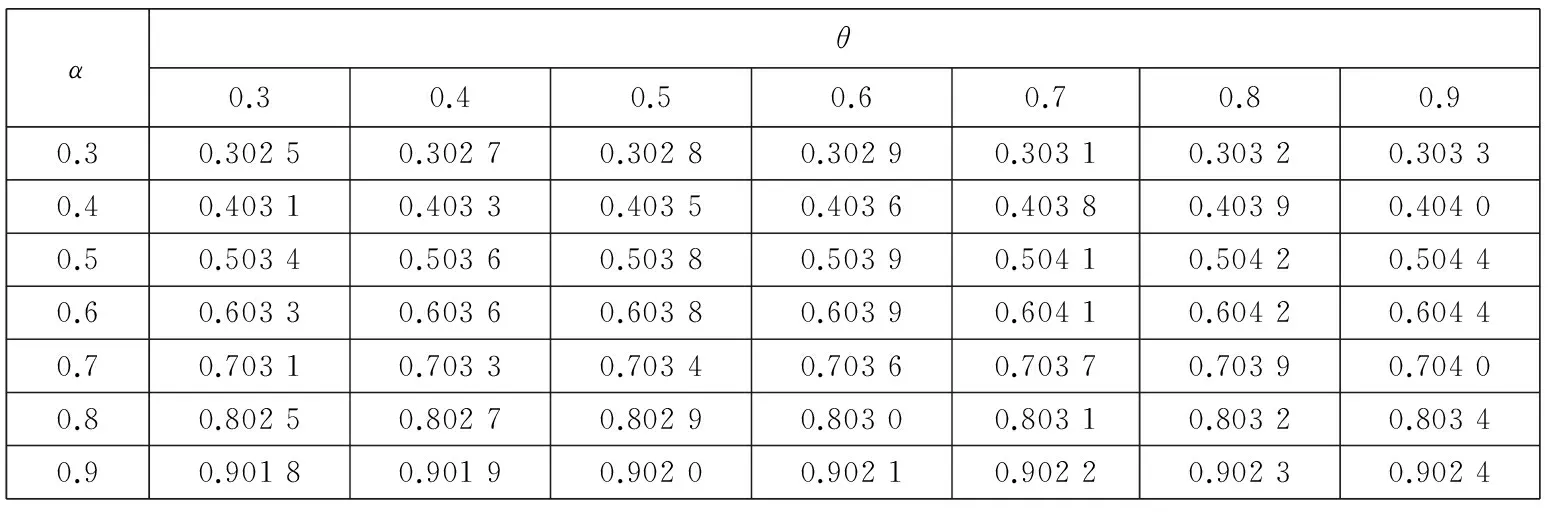
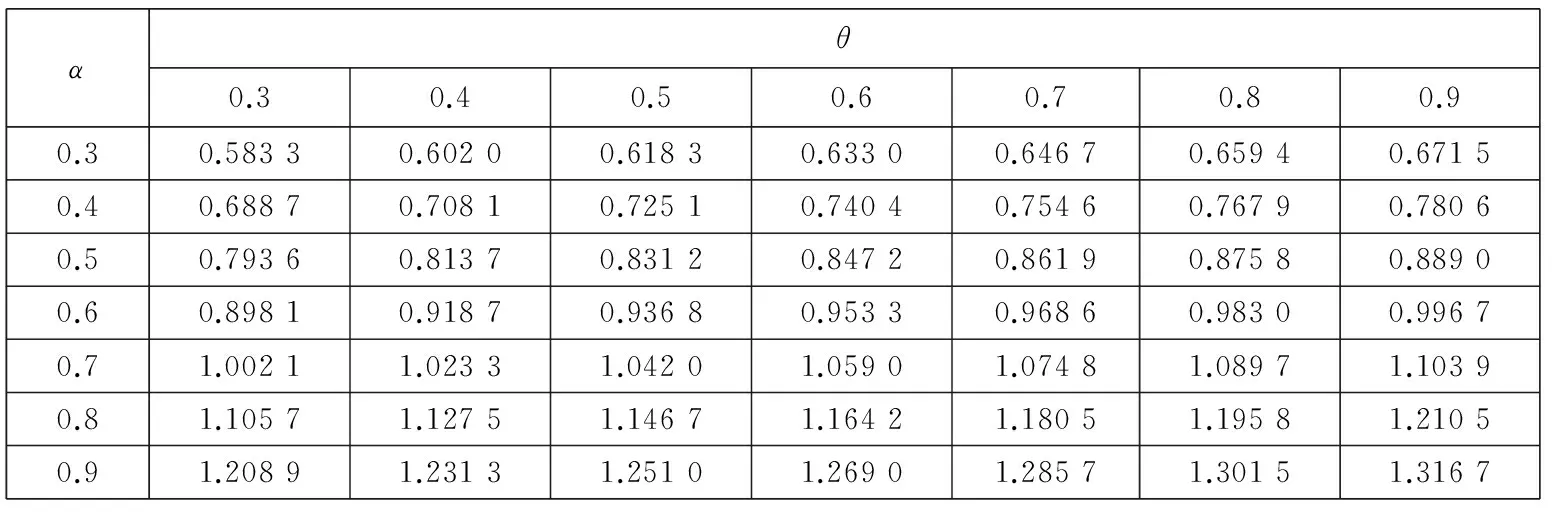
1.3市场环境对损失厌恶系数λ的影响
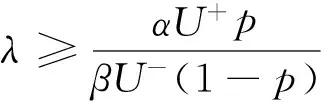
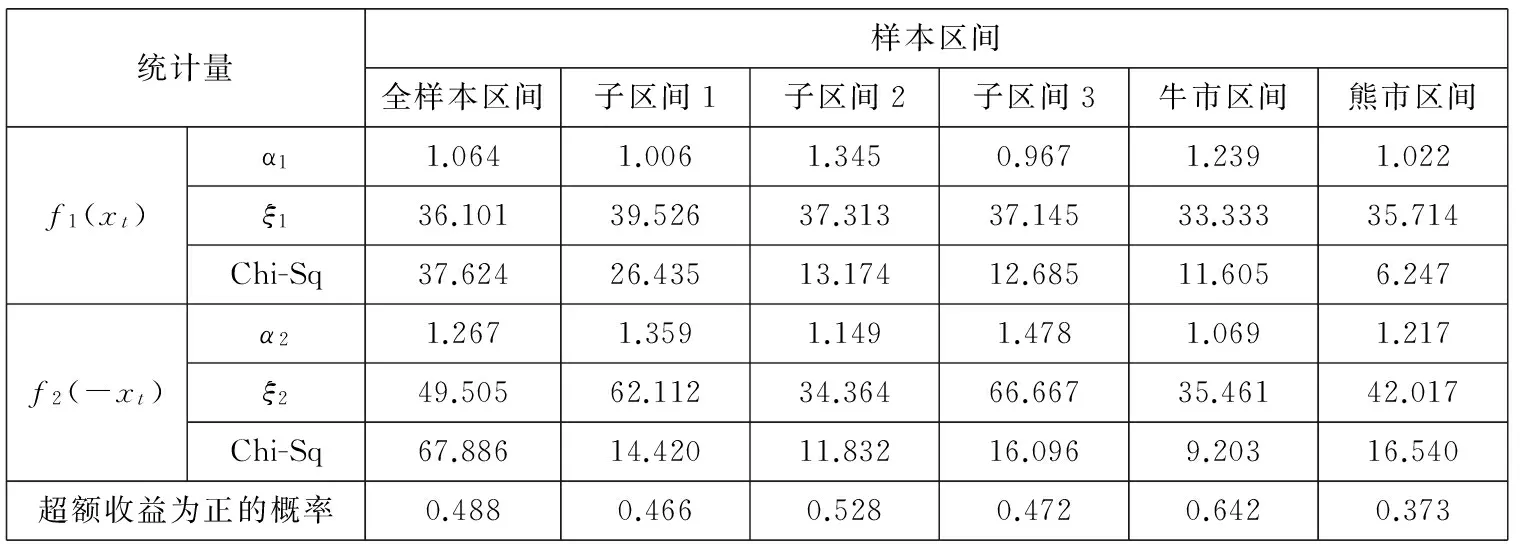
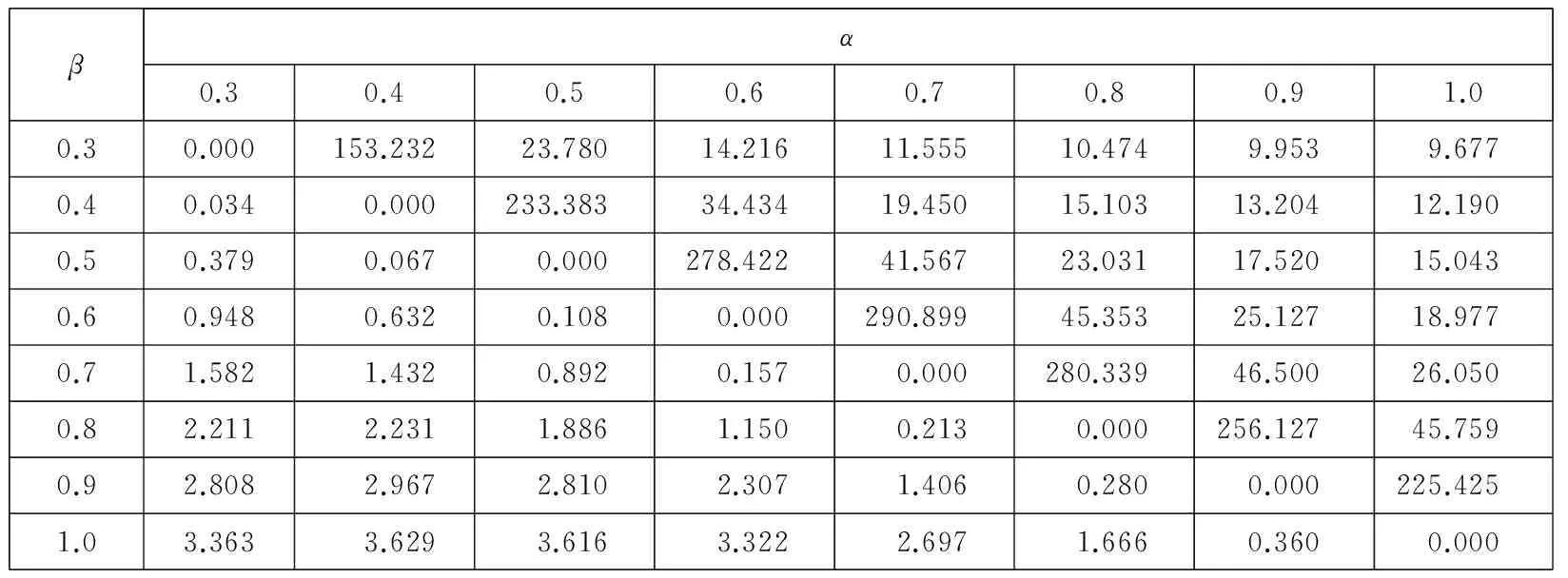
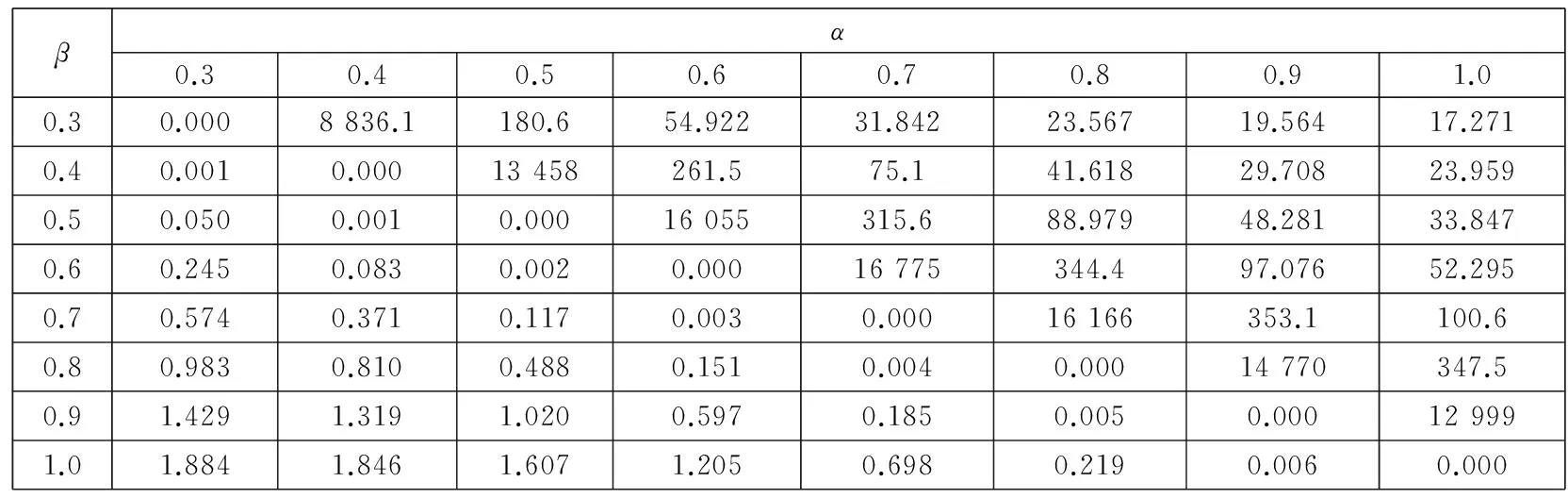
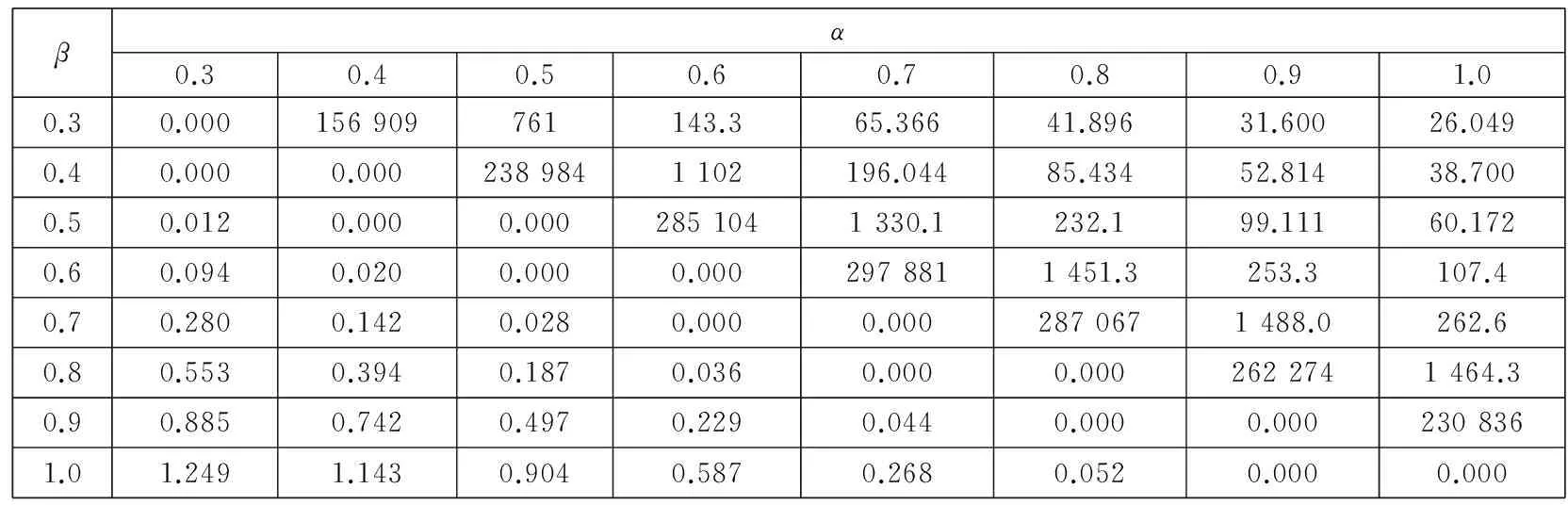
综上可知,λ的取值与U+, U-, p的变化有关.如果定义牛市为E(u+)>E(u-),E(p)>0.5,定义熊市为E(u+) 对方程(10)求关于β-α的偏导数,有 这说明当两个曲率参数的差增加时,投资于风险资产的比例也增加.例如当给定α的值时,增加β的值,投资者将会增加投资于风险资产的比例,这是因为随着两者之间差的增大也就意味着投资者对获利的变化更加敏感,而对损失变得更加迟钝,也就是会更加倾向卖出盈利的股票,持有亏损的股票,处置效应会更明显,总体上增加风险资产的持有. 2中国股票市场中的损失厌恶参数 实证研究 本部分使用证券收益和无风险利率研究α,β,λ的取值范围以及他们与θ的关系.在理想情况下,如果可以取得θt的时间序列,那么利用方程(9)通过非线性回归就可以直接得到α,β,λ的值.但是对于资产配置的真实数据很难取得,Hwang和Satchell[19]等通过实证发现θt与证券收益的相关性较高,相关系数为0.67,因此风险资产配置比例θt中的相当部分是内生于证券收益的,与此相比现金收益与θt之间的相关系数仅为0.02.因此,可以通过投资于证券的资产比例利用方程(9)得到α,β,λ的取值范围,本文使用的是周数据.通过该间接方法可以验证前面部分的理论推断与实证是否相符,也可以检验3个参数对其它参数改变的敏感程度. 2.1数据描述 对于资产配置而言,一般是以年或月度为计量单位的,但是由于我国的资本市场起步晚,若以年为单位收集数据,数量只有二十多个,从统计学的角度看不具有统计意义.中国市场有中国的特色,从“炒股票”这个词可见一斑,其主要以短线投机炒作为主.因此考虑统计方法对数据量的要求和中国市场的具体情况,在本文的研究中使用周数据作为研究对象,在计算超额收益率的时候,将银行的3个月定期存款利率作为无风险资产收益率. 本文使用的是上海证券市场自1998-09到2015-11的上证指数周数据,选取的是每周五的收盘价,共有868个样本,并取超额收益率后.将全样本区间均分为3个子区间,并将股票市场分为牛市和熊市两种状态.本文采用简单实用的波峰波谷的方法来判定牛市和熊市.找到相邻的波峰和波谷,计算两点之间的收益率,其变动如果超过50%,且满足时间间隔至少超过半年,则认为这个区间为牛市或熊市.考察在不同的市场情况下损失厌恶函数的变化情况,并出现了一些有意义的结果.表1是各个样本区间对数超额收益率的描述性统计. 表1 不同区间超额收益的统计描述 从上面的数据中可以看出,牛市期间的均值显著不为零.偏度方面,这6个期间均右偏.除了子区间1和3为低峰态 ,其他区间均为尖峰态,区间1和3为低峰态与股票尖峰厚尾现象并不完全一致,经计算验证,出现这种情况与时间序列的采样频率有关,当使用日数据进行统计时则会符合尖峰厚尾的特征.按照Jarque-Bera统计量的检验结果,在全部的6个样本区间均拒绝正态分布假设. 2.2参数估计 在分析之前首先要考虑数据的分布假设问题,正态分布是最常使用的概率分布,但是对于金融市场而言,已经有很多的理论和实证表明,金融数据的尖峰厚尾特性,使正态分布不能很好地刻画它,而且本文所要研究的损失厌恶中的资产配置问题本身就是不对称的问题,而正态分布的对称性对该问题的正确分析势必会产生影响.通过对数据基本统计性质的检验,它是拒绝正态分布假设的.因此考虑使用前文提到的Knight等[25]提出的KST分布对U+,U-进行估计. 表2 不同区间数据的KST分布参数估计 2.3损失厌恶参数α,β和λ对资产配置比例θ的影响 本节使用方程(9)计算θ的值,为简便起见假设W0=1;利用前面估计得到的中国股票市场的KST参数值计算方程(5)中的U+和U-.在计算时α的取值为0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0 ,β的取值为0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0 ,损失厌恶系数λ分别为1.50,2.25,3.00.之所以α,β的取值从0.3开始是参考了Holt和Laury[27]的研究,当曲率参数小于0.3左右时投资者为“非常风险厌恶”类型,鉴于参加证券市场投资的投资者都是具有较高风险偏好,因此将风险偏好的曲率参数从0.3开始算起,更符合实际情况. 表3、表4、表5显示当α>β时,投资比例θ的结果均大于1,不符合本文的前提条件.该结果与前面提出的命题结论是一致的.当α=β时,θ为0,即风险资产比例为0,所以α和β不能相等,K-T模型的α和β相等相矛盾.当β>α时,θ的值快速减少,而且在大多情况下小于1,这与实际情况和本文的假设相符.对于θ<1的情况还是有规律可循的,当β>α且α,β比较接近时,可以得到比较合理的资产配置比例,即在不允许买空的情况下θ取值在0到1之间. 表3 λ=1.5和全样本区间参数估计时,不同α,β值对θ的影响 从表3的结果中也可以发现,当λ取比较小的值时,α、β仅能在比较有限的区间内使得资产配置比例θ取值合理.从表3、表4、表5中可以看出,随着λ的增大,α、β可以在更大的取值范围内得到合适的资产配置比例θ,资产配置比例也随着α、β差值的增加而增加.更进一步可以说对于比较大的λ值,β-α的取值范围也可以大一些,由此可见两个曲率参数及其差的变化是与λ的变化有关的,即损失厌恶参数与风险厌恶参数具有内在关系. 表4 λ=2.25和全样本区间参数估计时,不同α,β值对θ的影响 表5 λ=3和全样本区间参数估计时, 不同α,β值对θ的影响 2.4β与资产配置比例θ的关系 为了进一步研究α,β,λ之间的关系,在给定α,λ,θ的情况下求解最优的β,优化的目标函数为 (14) 其中α,θ的取值范围为0.3到0.9,计算时采取的步长为0.1;λ的范围为1到3,并按照方程(5)计算U-,U+的值.为了比较不同时期损失厌恶参数的情况这里使用了子区间1、子区间2和子区间3的估计结果. 在相应的λ值下,β-α的符号不确定,在有些情况下是正的,有些情况是负的.之所以在不同区间选择的λ不同,是在求解β时不断实验的结果,比如在子区间2,λ为1.20时不能得出结果或者得出的结果中部分β-α小于零,而为1.21时,则均大于零,因此选择λ=1.21为其临界值,子区间1取λ=1与此相同.根据前面的分析,要求β-α>0,这就说明上面的两个λ值很接近损失厌恶系数的下界.Hwang和Satchell[19]对英国和美国股票市场的研究发现这两个成熟市场的损失厌恶系数的下界为1.5左右,与我国的市场有很大的差异.对于中国市场而言,损失厌恶系数的下界仅略大于1. 从表6~表11可见,β-α的大小随λ变化,并且是正相关的.从表6和表9可以看出,当λ取值很小时β-α之值一般小于0.05,也就是说β和α近似相等,与K-T推荐的曲率参数α=β=0.88接近,但此时λ的值为1或者很接近于1,也就是说损失厌恶不成立或者损失厌恶效应很微弱;λ取K-T试验得出的2.25时,最优的β-α之值在0.2左右.因此,从中国证券市场的实证结果来看,经典的K-T参数组合是不适用的,由此组参数得出的结论也是值得商榷的. 表6 给定α,θ和子区间1的KST分布参数估计值时β的最优值,λ=1 表7 给定α,θ和子区间1的KST分布参数估计值时β的最优值,λ=2.25 表8 给定α,θ和子区间1的KST分布参数估计值时β的最优值,λ=3 表9 给定α,θ和子区间2的KST分布参数估计值时β的最优值,λ=1.21 表10 给定α,θ和子区间2的KST分布参数估计值时β的最优值,λ=2.25 表11 给定α,θ和子区间2的KST分布参数估计值时β的最优值,λ=3 从上述的计算结果也可知,资产配置比例θ对于曲率参数的绝对值变化不敏感,但是对于β-α的变动很敏感,很小的β-α变化会导致投资比例产生很大的波动,经过计算发现θ对β-α的斜率一般是大于10的,因此确定合理的β,α值对于实际应用十分重要.当固定β-α时,随着λ的增大,风险资产配置比例会变小.这与前文的推导结果是一致的. 2.5牛市和熊市对损失厌恶参数的影响 与前面的分析方法相同,计算熊市和牛市区间的β,具体数据见表12—表15.和前面的分析结果一致,计算结果发现牛市区间的损失厌恶系数下界提高,利用上海股票市场的数据得到的结果为2.19,熊市区间的λ的下界降低,计算的结果为0.59左右,也就是熊市期间同等财富的损失带来的负效用要小于牛市期间同等财富的损失带来的负效用,可以解释为投资者此时对于损失已经习以为常,见怪不怪,对损失的敏感度大大降低,这与大部分投资者的真实感受基本一致,对熊市期间的损失越来越不关心,即损失厌恶的程度与损益的参考点是密切相关的.这些结果表明损失厌恶系数应该是市场景气程度的函数,因此λ是时变的,这与Thaler等[16]的观点是一致的,认为损失厌恶系数与投资者前期的损益有关,考虑多期投资时投资者的损失厌恶系数在一定程度上是自相关的. 表12 给定α,θ和牛市区间KST分布参数估计值时β的最优值,λ=2.19 表13 给定α,θ和牛市区间KST分布参数估计值时β的最优值,λ=2.25 表14 给定α,θ和熊市区间KST分布参数估计值时β的最优值,λ=0.59 表15 给定α,θ和熊市区间KST分布参数估计值时β的最优值,λ=2.25 损失厌恶的曲率参数β在熊市的时候比在牛市的时候要大,其差异一般在0.2~0.35之间.随着β的增大,关于损失的效用函数曲线整体向左上移动,也就是对于损失更加不敏感,同样的小损失在牛市期间带给投资者的负效用的绝对值比在熊市期间要大的多,但对于大的损失在牛市期间带给投资者的负效用的绝对值比在熊市期间要大但程度减少.直观上可以这样理解,当看到别人股票都在上涨,而自己持有的资产却在损失时,这种对比带给投资者更大的痛苦,熊市期间对于损失已经没有那么敏感,因此,处于熊市的时候投资者更倾向于持有已亏损的风险资产.从数据可以看出,当λ=2.25时,熊市计算数据中的β一部分是大于1的,尤其是对于K-T推荐的α=0.88情况, β都是大于1的,这意味着投资者在熊市期间,或者是由于前期的损失或者由于可能面临比较大的损失,投资者面对损失时也是风险厌恶的,由于本文已将α、β限定为小于1,所以不对该情况进行讨论. 2.6牛市和熊市中的损失厌恶系数 损失厌恶系数的下界由下式确定 (15) 使用上式计算不同α、β组合下不同区间的损失厌恶系数下界,结果如表16所示.从表中可以看出,λ的下界随着β-α的增加而增加,比如α=0.8,β=0.88时,牛市时的λ下界为2.512,而当β=0.96时,λ则增加至2.963 3,也就是说在市场状态给定的情况下,风险喜好程度的减弱伴随着损失厌恶程度的增加,两者之间存在内在联系.其次,市场繁荣时候的损失厌恶系数下界几乎是熊市时损失厌恶系数下界的4倍,并以牛市时为最高,这种变动说明损失厌恶效用系数应该是随时间或市场状态变化的,而且变化幅度很大,不能忽略这种变化.从表16中也可以看到随着β增加,损失厌恶系数下界是增加,从式(15)来看,λ随着β的增加而减少,之所以会出现这种情况是U-会随着β的增加而减少且减少的速度更快.另外,与英美的成熟市场相比[19]中国股票市场所体现的损失厌恶系数明显偏低,英美市场上λ的下界基本在3~5之间,即使与K-T推荐的λ=2.25相比,中国投资者的损失厌恶系数下界也明显偏低.中国与成熟市场损失厌恶系数的这种明显差异是由于投资者的风险偏好引起还是由于资本市场的结构趋势的不同引起是值得进一步研究的问题. 表16 不同区间的损失厌恶系数下界 3结束语 通过实证分析,发现如果曲率参数α、β是相等的,就会导致不合理的风险资产配置,因此α、β应该是不相等的,并且证明应该有α<β,表明投资者对收益的改变比对损失的改变更敏感,与Kahneman和Tversky[2]提出的损失曲率和收益曲率相等的结论不一致;其次,风险资产的最优配置比例与β-α和λ有关,β-α与θ成正比的关系,说明当两个曲率参数的差增加时,投资于风险资产的比例也增加.因为随着两者之差的增大,投资者对获利的变化更加敏感,而对损失变得更加迟钝,会更加倾向卖出盈利的股票,持有亏损的股票,即处置效应会更明显,总体上增加风险资产的持有;λ与θ成反比的关系,这是由于当损失使投资者的负效用增加时,也就是存在比较大的λ时,投资于风险资产的比例会下降;最后,本文发现损失厌恶系数λ的下界随着熊市和牛市的变化有显著的差别,牛市时的下界远大于熊市的下界,也就是说投资者在牛市中的损失厌恶系数最大,在熊市中的损失厌恶特征不明显.市场行情的走势会影响投资者的心理,投资者在牛市中的损失会产生更多的负效用,当其他投资者分享获利的欢乐时,此时的损失会使投资者遭受更多的痛苦;反之熊市时亦然. 本文使用风险资产收益与风险资产比例之间的关系间接计算出损失厌恶参数的变化范围,但是还不能精确计算出不同类型决策者/投资者的损失厌恶参数,因此未来使用更有效的方法获取更为准确的损失厌恶参数及曲率参数的变化规律是值得探索的方向;研究不同地区和市场之间损失厌恶程度的差异及其规律也是很有意义的工作. 参 考 文 献: [1]Tversky A, Daniel K. Advances in prospect theory: Cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5 (4): 297-323. [2]Kahneman D, Tversky A. Prospect theory: An analysis of decision making under risk[J]. Econometrica, 1979, 47(2): 263-291. [3]Nathan N, Daniel K. The boundaries of loss aversion[J]. Journal of Marketing Research, 2005, 42(2): 119-128. [4]Benartzi S, Thaler R H. Myopic loss aversion and the equity premium puzzle[J]. The Quarterly Journal of Economics, 1995, 110(1): 73-92. [5]Hardie B G S, Eric J J, Peter S F. Modeling loss aversion and reference dependence effects on brand choice[J]. Marketing Science, 1993, 12(4): 378-394. [6]张维, 张海峰, 张永杰, 等. 基于前景理论的波动不对称性[J]. 系统工程理论与实践, 2012, 32(3): 458-465. Zhang Wei, Zhang Haifeng, Zhang Yongjie, et al. Volatility asymmetry based on prospect theory[J] . Systems Engineering-Theory & Practice, 2012, 32(3): 458-65. (in Chinese) [7]周嘉南, 黄登仕. 损失厌恶能否解释“好消息提前, 坏消息延后”[J]. 管理科学学报, 2009, 12(6): 125-138. Zhou Jianan, Huang Dengshi. Good news early, bad news late: The impact of oss aversion[J]. Journal of Management Sciences in China, 2009, 12(6): 125-138. (in Chinese) [8]Harbaugh W T, Drause K, Vesterluad L. Risk attitudes of children and adults: Choices over small and large probability gains and losses[J]. Experimental Economics, 2001, 5 (1): 53-84. [9]Chen M K, Venkat L, Laurie R S. How basic are behavioral biases? Evidence from capuchin monkey trading behavior[J]. Journal of Political Economy, 2006, 114(3): 517-537. [10]Tom S M, Fox C R, Trepel C, et al. The neural basis of loss aversion in decision-making under risk[J]. Science, 2007, 315(26): 515-518. [11]Berkelaar A B, Kouwenberg R, Post T. Optimal portfolio choice under loss aversion[J]. Review of Economics and Statistics, 2004, 81(4): 973-987. [12]Barberis N, Huang M. Mental accounting, loss aversion, and individual stock returns[J]. Journal of Finance, 2001, 56(4): 1247-1296. [13]Ang A, Bekaert G, Liu J. Why stocks may disappoint[J]. Social Science Electronic Publishing, 2000, 76(3): 471-508. [14]Camerer C F, Ho T H. Violations of the betweenness axiom and nonlinearity in probability[J]. Journal of Risk and Uncertainty, 1994, 8(2): 167-196. [15]Wu G, Gonzalez R. Curvature of the probability weighting function[J]. Management Science, 1996, 42(12): 1676-1690. [16]Thaler R H, Tversky A, Kahneman D, et al. The effect of myopia and loss aversion on risk taking: An experimental test[J]. Quarterly Journal of Economics, 1997, 112 (2): 647-661. [17]Patricia T. The effects of loss aversion on trade policy: Theory and evidence[J]. Journal of International Economics, 2009, 78(1): 154-167. [18]Booij A S, van Praag B M S, van de Kuilen G. A parametric analysis of prospect theory’s functionals for the general population[J]. Theory and Decision, 2010, 68(1/2): 115-148. [19]Hwang S, Satchell S E. How loss averse are investors in financial markets?[J]. Journal of Banking & Finance, 2010, 34(10): 2425-2438. [20]Dimmock S G, Kouwenberg R. Loss-aversion and household portfolio choice[J]. Social Science Electronic Publishing, 2010, 17(3): 441-459. [21]Wanga C X, Websterb S. The loss-averse newsvendor problem[J]. Social Science Electronic Publishing, 2009, 37(1): 93-105. [22]王佳, 金秀, 苑莹. 股票市场投资者损失厌恶特征实证研究[J]. 财会通讯, 2015, (26): 3-6, 129. Wang Jia, Jin Xiu, Yuan Ying. Empirical research of investors’loss aversion characteristics in stock market[J] . Communication of Finance and Accounting, 2015, (26): 3-6, 129. (in Chinese) [23]Wakker P, Deneffe D. Eliciting von Neumann-Morgenstern utilities when probabilities are distorted or unknown[J]. Management Science, 1996, 42(8): 1131-1150. [24]Abdellaoui M, Bleichrodt H, Paraschiv C. Loss aversion under prospect theory: A parameter-free measurement[J]. Management Science, 2007, 53(10): 1659-1674. [25]Knight J L, Satchell S E, Tran K C. Statistical modelling of asymmetric risk in asset returns[J]. Applied Mathematical Finance, 1995, 2(3): 155-172. [26]Fishburn P C, Kochenberger G A. Two-piece von-New mann-Morgenstern utitity functions[J]. Decision Seiences, 1979,10(4): 503-518. [27]Holt C A, Laury S K. Risk aversion and incentive effects[J]. Social Science Electronic Publishing, 2002, 92(5): 1644-1655. Loss aversion’s parameters based on asset allocation ZHANGXiao-tao1,2,PANQi1,LIYue-lei1,2 1. College of Management and Economics, Tianjin University, Tianjin 300072, China;2. Key Laboratory of Computation and Analytics of Complex Management Systems, Tianjin 300072, China Abstract:The curvature parameters and coefficient of loss aversion utility function proposed in prospect theory by Kahneman and Tversky are researched by means of asset allocation under a single period economic system with aloss aversion investor. This article proved that the curvature parameters, α,β, should be not equal and have a relationship of β-α>0 and that the loss aversion coefficient, λ, is not a constant and changes with market environments. The ratio of risk assets varies with the difference of β,α and increases with the difference. These theoretical analyses are tested with data from China’s stock market; the empirical result is consistent with the theoretical analysis. An interest finding is that the lower bound of loss aversion coefficient of China’s stock market is far less than that of developed counties. Key words:asset allocation; loss aversion utility; loss aversion parameter 收稿日期:①2012-11-17; 修订日期:2015-04-01. 基金项目:国家自然科学基金资助项目 (71071109; 71320107003; 71201113). 作者简介:张小涛(1975—), 河北河间人, 博士, 副教授, Email: zxt@tju.edu.cn 中图分类号:F830.91 文献标识码:A 文章编号:1007-9807(2016)05-0056-12