几何公差标注的教学技巧研究

李景阳，梁　萍，马　霄（河南机电高等专科学校，河南 新乡 453003）



几何公差标注的教学技巧研究

李景阳，梁萍，马霄
（河南机电高等专科学校，河南 新乡 453003）

摘要：几何公差的标注是《互换性与技术测量》课程中的重要组成部分，是教学中的重点和难点。文章分析了几何公差标注的特点，对几何公差标注在教学中易出现的问题进行了详细解析，进而提出了“3-Question”式的解决方法，经教学实践验证，此方法对于学生掌握正确标注几何公差具有显著的提升效果。

关键词：几何公差；标注；教学；互换性与技术测量

0　引言

几何误差会影响零件的工作精度、联接强度、运动平稳性、密封性、耐磨性、噪声和使用寿命等，并影响着该零件的质量和互换性。因此，在设计时必须根据零件的功能要求和制造的经济性，在零件图样上标注出几何公差，以限制几何误差。所以几何公差标注在零件的设计与制造过程中起着重要的作用。

几何公差标注也是教学中的重点。

几何公差从属于《互换性与技术测量》课程[1]，专业不同，教学大纲的要求也不同，教学内容或有侧重、但是不管是机类还是近机类专业，对于几何公差标注的要求都是一样的，这是因为无论哪个专业只要是从事机械行业，在工作中都要看图纸，而图纸上很重要一部分内容就是几何公差，如图1所示。因此，几何公差的标注能力是《互换性与技术测量》课程的重要内容，是学生必须要掌握的技能。

1　几何公差标注的特点

1.1公差项目多

根据GB/T1182-2008《几何公差形状、方向、位置和跳动公差标注》的规定，几何公差项目有14个，分为形状、方向、位置和跳动公差，每一类在概念、标注等方面又有诸多不同[2]。

图1　轴零件图

1.2公差代号多

标准规定，在技术图样上几何公差应采用几何公差代号进行标注[3]。几何公差代号包括：公差框格、指引线、公差项目符号、公差数值、基准代号和公差原则等，如图2所示。

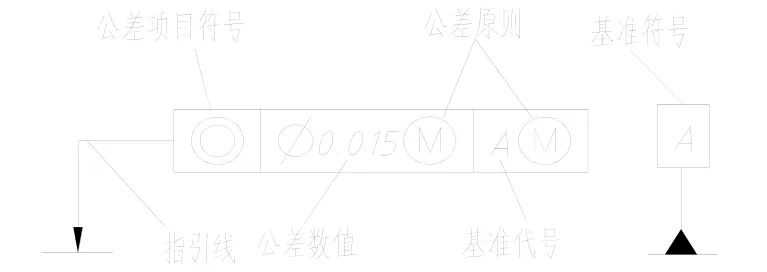
图2　几何公差标注方法

2　公差标注中的问题及解决方法

2.1主要问题

如上所述，几何公差项目众多，公差代号多且涉及不同的要求，每一项都是一个知识点，而且几何公差所涉及的点、线、面等几何要素在机械零件上又有不同的体现，因此学生对几何公差的标注极易出错，其中，最易出错的主要有三个方面：

1）指引线的位置：学生在标注时不知道箭头的指引位置和方向；

2）公差数值的符号：学生在标注时不知道公差值之前是否需要添加直径符号“Φ”；

3）基准的标注：学生在标注时对于基准认识不够，不知有没有基准、属于什么基准、怎么标注，从而导致基准的遗漏、多余或错误标注。

这三方面内容涵盖几何公差的主要特征，非常重要，同时这些内容又比较抽象，不太容易理解。

2.2问题解析

出现这些问题，最主要的原因是对知识点理解得不够深刻。要想完整、正确、清晰地标注几何公差，就要对这些知识点详细了解，而在目前教学中这些知识点比较分散，现将其整理并分析如下：

1）指引线的位置：指引线用来指示公差对象即被测要素。国标规定：①当被测要素为轮廓要素时，指引线的箭头应置于被测要素的轮廓线的延长线上，并与尺寸线“明显错开”，如图1中的圆跳动和圆度的标注。②当被测要素为中心要素时，指引线的箭头应与确定中心要素的轮廓的尺寸线对齐，如图1中的键槽对称度的标注。

2）公差数值的符号：在几何公差的标注中，是否加“Φ”由公差带形状决定。公差数值前有时会加直径符号“Φ”。国标规定：如果该几何公差的公差带形状为圆、圆柱体或球体内的区域，需要在公差数值前添加直径符号“Φ”（球体添加“SΦ”），因为此时公差数值表示的是公差带的直径大小。如图3中同轴度的标注，很多人忘记标注“Φ”，就是因为对这一点认识不够。

那么哪些公差带的形状是圆、圆柱体或球体呢？这就需要对每一个公差项目有详细的了解，相关书籍有详细介绍，不再一一赘述，在此只分析需要加“Φ”的几种公差项目：

① 同轴度

同轴度的被测要素是轴线，其公差带的形状为“以基准轴线为轴线、直径为公差数值的圆柱面内的区域”，故同轴度必须加“Φ”。如图3所示。

② 在任意方向上的直线度

直线度公差带有3种情况：在给定平面内、在给定方向上和在任意方向上，其中前两种情况公差带形状为非圆结构，公差值前不用加“Φ”。但是，如果被测要素为“轴线”时，即“在任意方向上”都提出了公差要求，此时需要加“Φ”，如图4所示。

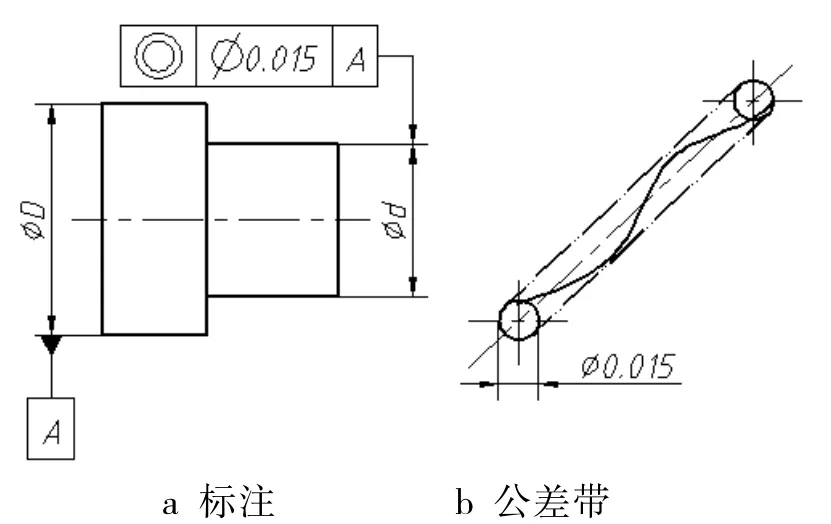
图3　同轴度示例

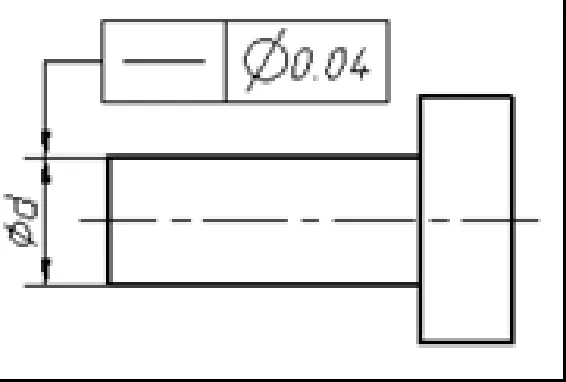
图4　直线度示例

③ 在任意方向上线对面的垂直度

根据被测要素和基准要素的不同，垂直度公差有面对面、面对线、线对线和线对面4种情况，其中，前两者都不需要添加“Φ”，后两者中存在加“Φ”的情况，其中线对面的情况较为常见。

线对面的垂直度又分为指定方向、任意方向两种，其中“任意方向”需要添加“Φ”。如图5所示。

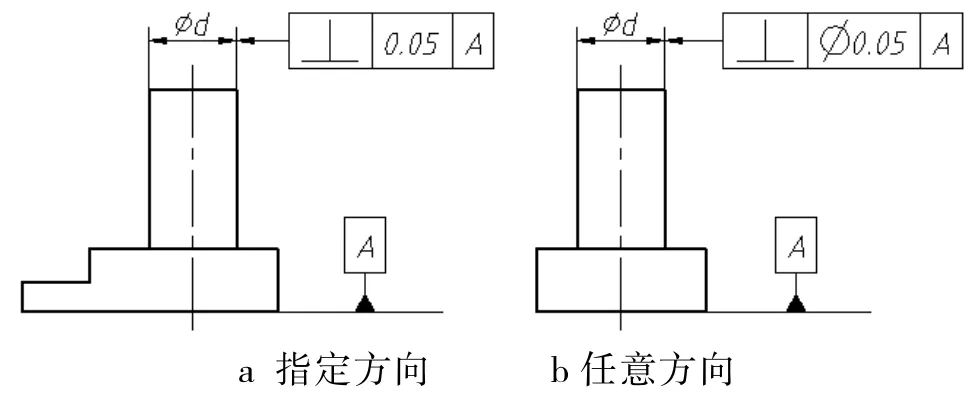
图5　垂直度示例

那么，在什么情况下为指定方向、什么情况下为任意方向呢？主要看被测轴线朝不同方向的偏置对使用性能的影响，如果在圆周任意方向上的偏置对使用性能影响是等量的，就为任意方向，否则为指定方向。通常情况下与轴结构有关系，如果这个轴的结构在圆周方向关于中心对称，就是任意方向，如图5b。如果轴结构在圆周方向上有明显的不对称，那就为指定方向了，如图5a所示。

④ 某些情况下的位置度

位置度公差加不加“Φ”，应视使用要求而定。如果被测要素是三基面体系定位的点要素，则需要添加“SΦ”，因为此时公差带的形状是以理想位置点为圆心的球体内的区域，公差值表示该球体公差带的直径，如图6所示。

图6　位置度示例

3）基准的标注

基准的标注需要注意两点：第一，判断有无基准。形状公差无基准，方向、位置和跳动公差有基准；第二，如果有基准，基准是中心要素还是轮廓要素，这一点与指引线的要求一样，基准符号连线的位置是不一样的，此处不再赘述。

2.3解决方法

以上是几何公差标注中最容易出错的三个方面的内容，可见要想正确标注几何公差最好要求熟悉每一个公差项目，但是由于公差项目多、概念多、知识点多，在教、学过程中就容易感到繁琐、疲惫，从而影响教、学效果。

为了让学生在学习时能够很方便、快捷掌握公差标注，在上述知识点整理、分析基础上，提出了“3-Question”式的教学、学习方法，即带着以下三个问题去学习每一个公差项目：

①被测要素是什么？属于中心要素还是轮廓要素？

②公差带形状是什么，圆、圆柱体或其它形状？

③有无基准？基准属于中心要素还是轮廓要素？

首先正确回答这三个问题，然后再根据以上分析，按照国标要求，做出相应的标注即可。按照此方法，就能够快速的掌握几何公差的标注。可以通过下例进行说明。

如图7所示，圆度、圆柱度的被测要素都属于轮廓要素，公差带的形状也不属于圆形、圆柱和球体，而且是形状公差，无基准，故标注如上；垂直度的被测要素为圆柱体端面，属轮廓要素，箭头垂直指向被测要素延长线，公差带为两平行平面之间的区域，故公差值前没有“Φ”，有基准，而且基准是圆柱体轴线，属中心要素，所以基准B符号与直径线对齐标注；同轴度被测要素为Φd孔的轴线，指引线箭头与Φd尺寸线对齐，公差带是直径为0.05的圆柱体内的区域，所以公差值前要有“Φ”，被测要素是ΦD孔的轴线，为中心要素，A要与ΦD尺寸线对齐。

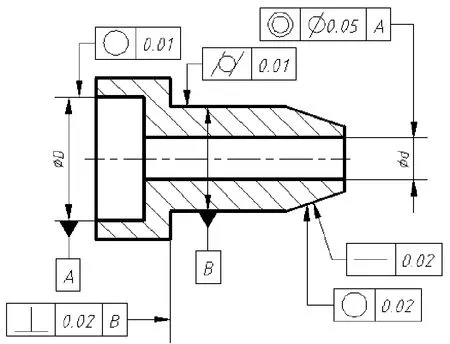
图7　综合示例

3　结语

通过对几何公差标注的重要性、特点、疑难点和常见错误进行详细梳理和分析，结合教学实践，找到了一种能快速、有效地学习、掌握几何公差正确标注的方法。只要按照这个方法进行学习、读图和标注，就能够最大限度地减少错误。此方法经教学实践验证，对于学生掌握几何公差的标注具有显著的提升效果。

（责任编辑 吕春红）

参考文献：

[1]马霄,任泰安.互换性与技术测量[M].南京：南京大学出版社，2011.

[2]马霄,田长留.互换性与技术测量课程教学改革的研究与实践[J].河南机电高等专科学校学报,2010(6).

[3]GB/T1182-2008,几何公差形状、方向、位置和跳动公差标注[S].

Research on Geometrical Tolerancing Label Teaching Skill

LI Jing-yang, et al
(Henan Mechanical and Electrical Engineering College, Xinxiang 453003, China)

Abstract:As a very important component of Interchangeability and Technology-based Measurement course, labeling the Geometrical Tolerancing is always a key and difficult point. A thorough analysis was made on the characteristic and difficult point , and also the problem during teaching the Geometrical Tolerancing label, then a 3-question solution was raised. This solution was validated through the teaching practice, can significantly help students to learn to label the Geometrical Tolerancing correctly.

Key words:geometrical tolerancing; table; teaching; interchangeability and technology-based measurement

中图分类号：G642.0

文献标识码：A

文章编号：1008-2093(2016)01-0073-03

收稿日期：2015-10-12

作者简介：李景阳（1983―），男，河南林州人，讲师，工学硕士，主要从事机械设计及理论研究。