基于改进SFLA-PF算法的OFDM系统目标跟踪

曹向东，毛永毅

(西安邮电大学 电子工程学院， 陕西 西安710061)

基于改进SFLA-PF算法的OFDM系统目标跟踪

曹向东，毛永毅

(西安邮电大学 电子工程学院， 陕西 西安710061)

摘要:在OFDM通信系统中，为了解决非线性的目标跟踪问题,提出了基于改进混合蛙跳算法(SFLA)和粒子滤波算法(PF)相结合的方法来研究动态目标跟踪技术。首先利用高斯变异的局部搜索能力强和柯西变异的全局搜索能力强等优点对混合蛙跳算法进行改进，然后用改进后的混合蛙跳算法来优化粒子滤波算法进行动态跟踪，其优点不需要重采样步骤，有效地保持了粒子的多样性和有效性。仿真结果表明，该算法能够有效实现动态目标跟踪，并且跟踪效果优于同等条件下的混合蛙跳算法和粒子滤波算法。

关键词:OFDM；混合蛙跳；粒子滤波；高斯变异；柯西变异

在军事以及民用领域中,寻求可靠而又精确的目标位置一直是动态跟踪技术研究的主要目的。因此对于动态目标跟踪的研究引起了国内外很多学者的高度重视[1]。同时基于常规的卡尔曼滤波算法通常要求系统是线性高斯型的,所以不能直接用来解决非线性等问题。于是文献[2]提到基于粒子滤波的目标跟踪，主要针对粒子滤波的动态模型与观测模型进行研究，并将图像分割与随机森林分类器引入粒子滤波跟踪算法之中，来提高跟踪性能。文献[3]提出了粒子滤波优化目标跟踪算法，这种方法是基于PFTMT算法与模板匹配算法跟踪精度高的优点相结合来提高粒子滤波跟踪精度；文献[4]提出基于粒子群和M-H粒子抽样粒子滤波的跟踪技术研究，它主要采用分布式结构，抑制粒子退化现象，从而使粒子快速收敛，进而提高跟踪精度；文献[5]提出了基于群智能算法的动态目标跟踪技术研究，利用智能算法中粒子个体间相互具有联络、通信的优良特性，将其融入到粒子滤波算法中进行跟踪；文献[6-7]改进群体智能算法，是通过增加变异因子的方法来提高混合蛙跳算法的搜索寻优性能。

本文介于粒子滤波算法本身个体与个体之间没有交互性的性质，进而引入了个体与个体之间具有交互性和通信机制的蛙跳算法来优化粒子滤波算法，首先对蛙跳算法引入高斯变异和柯西变异，提高了算法收敛速度和引导个体快速跳出局部最优，再把改进的SFLA-PF算法运用在OFDM系统中进行动态目标跟踪，验证表明，该算法表现出很好的跟踪效果。

1算法描述

1.1粒子滤波算法

粒子滤波(Particle Filter，PF)是从20世纪90年代开始发展起来用于解决目标跟踪问题的新算法。也是目前解决非线性跟踪问题的核心算法。

假设描述非线性系统的状态方程为

xk=f(xk-1,uk-1),Zk=h(xk，vk)

(1)

贝叶斯估计是利用先验概率分布函数来构造系统的后验概率分布函数的基本思想，同时递推过程也是由先验概率来逼近后验概率，假设此状态下初始概率密度函数的表达式为

p(x0|z0)=p(x0)

(2)

则在此状态下的预测方程为

p(xk|z1:k-1)=∫p(xk|xk-1)p(xk-1|z1:k-1)dxk-1

(3)

状态的更新方程为

(4)

(5)

其中

(6)

(7)

1.2蛙跳算法

1.2.1基本的蛙跳算法

蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)于2003年由Eusuff和Lansey提出的为解决组合优化问题的智能算法。作为一种新型的仿生物学智能优化算法，该算法具有概念简单、计算速度快、全局寻优能力强、易实现等优点，因此被广泛用于解决工程领域里寻求最优解等问题。

在一个S维的目标寻优搜索空间里，让随机产生的N只青蛙个体组成初始群体p={x1,x2,…,xN},则第i只青蛙个体可以表示为xi=[xi1,xi2,…,xis]。

在初始种群生成之后，让种群内的所有青蛙个体的适应值按照降序排列，同时把种群内部适应值最优的个体标记为xg；再将整个种群分成m个子群，同时每个子群中包含n个个体，并满足关系N=m×n,设Mk为第k个子群的集合，分配过程如下

Mk={xk+m(l-1)∈p|1≤l≤n},1≤k≤m

(8)

然后把每一个子群中适应值最好和最差的个体分别标记为xb和xw，同时把整个种群中适应值最好的个体标记为xg，然后再对每个子群中的xw个体循环进行局部搜索，具体的更新策略方式如下

D=r·(xb-xw)

(9)

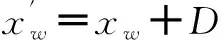
(10)

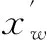
1.2.2改进的蛙跳算法

本文提出了改进蛙跳算法(SFLA)，一方面基于该算法在寻优过程中局部搜索能力较弱，引入了柯西变异，利用它的全局搜索能力，易引导个体跳出局部最优，避免了算法陷入局部最优的缺陷[8]，另一方面基于SFLA在寻优中容易陷入早熟收敛，引入了高斯变异，利用它较强的局部搜索能力，提高了该算法的收敛速度，很好地避免了发生早熟收敛的缺点[9]。两种变异算子相互结合使用，提高了算法的寻优精度和收敛速度。

常用的变异算子有4种，包括高斯变异算子、柯西变异算子、混沌变异算子、levy变异算子等。本文为了避免SFLA算法陷入局部最优和发生早熟收敛现象，选用高斯变异和柯西变异。

高斯分布又称为正态分布，是研究概率论等学科的一项重要分布函数。通常将高斯变异记为N(μ,σ2),μ为连续变量的期望，σ2为变量的标准方差。则概率密度函数为

(11)

高斯分布可记为

(12)

通过式(11)可以看出，高斯分布密度函数关于x=μ对称，同时在x=μ时函数取得最大值，曲线呈现中间高两边低的正态分布趋势。从方程中还可以看到，当μ=0，σ2=1时，称此为标准高斯分布，记为N(0，1)

(13)

柯西分布通常表示为C(β，λ)，β和λ表示位置参数，概率密度函数可描述如下

(14)

其密度函数可表示为

(15)

从式(15)可以看出，曲线关于x=β对称，当β=0，λ=1时，柯西分布记为C(0,1),此时被称为标准柯西分布，其表达式为

(16)

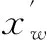
改进后的具体为

D=r·(xb-xw)

(17)

D=D+D·Ui

(18)

(19)

其中：Ui=(Ui1,Ui2,…,UiD)

1.3改进的SFLA-PF算法的动态目标跟踪

介于粒子滤波本身个体不具有交互性，而混合蛙跳算法中个体具有交互性和相互联络的通信机制，所以将改进后性能优越的蛙跳算法融入到粒子滤波算法当中，让粒子之间相互不再独立，而具有合作共存的意识，并用于目标跟踪。根据前面对两种算法的具体介绍，可以得出改进SFLA-PF算法的具体实现步骤如下：

第3步：适应度值更新。按照式(6)计算种群中每个个体的适应度值。并用式(7)计算个体的适应度值标准化。

第4步：判断子群。判断当前种群中出现的最优个体是否与上次进化时得到的最优个体相同，如果相同子群在进行局部搜索时就采用柯西变异算子，如果不同，就选用高斯变异算子。

第5步： 更新目标状态。对子群进行局部搜索，确定xg和xb的值。并采用式(17)、(18)和(19)更新方法对xw进行更新，重复此操作，直到子群都满足收敛条件为止。

第7步：在OFDM系统中通过计算移动台到达3个基站的TOA值，然后用TOA值得到TDOA的值。

第8步：利用上述得到的TDOA值结合改进的粒子滤波(SFLA-PF)算法实现对移动台的位置估计，进而实现对动态目标的定位跟踪。

2仿真及分析

2.1仿真条件

为了检验本文所提跟踪算法的合理性以及该算法性能的优越性，将改进的SFLA-PF算法和PF算法应用到OFDM通信系统中进行跟踪对比，并利用仿真软件对这两种跟踪算法进行仿真分析。

算法仿真过程中采用典型的7小区组成的蜂窝结构,服从T1P1信道模型，服务基站BS1(0,0)位于小区中心,小区半径为3 km,取粒子数N=100(经验证为较优值)，移动台由坐标(200，200)处出发,沿与x坐标轴正方向成60°的方向匀速运动，初速度为24 m/s，信噪比为30 dB。OFDM信号仿真参数：取载波数为128，采样周期为50 ns，OFDM带宽为20 MHz，天线单元数为6，天线间隔0.5 m。

2.2状态描述

状态方程表达式为

(20)

观测方程表达式为

zk=h(xk)+nk=

(21)

位置的均方根误差表达式如下

(22)

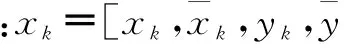
2.3仿真结果分析

图1为本文算法、混合蛙跳算法和粒子滤波算法在以上条件下的动态目标跟踪仿真图，横坐标表示移动台沿x轴方向的运动距离，纵坐标表示沿y轴方向移动台与基站的距离，从图中可以看到本文算法跟踪效果非常优越，跟踪轨迹基本都紧靠真实运动轨迹，且跟踪性能稳定，基本能够准确估计目标真实运动状态，相比之下，跟踪效果明显优于混合蛙跳算法和粒子滤波算法。以上也充分说明了本文改进算法提高了粒子间的合作共存能力，保持了粒子的多样性和有效性，也很好地抑制了粒子退化等问题。

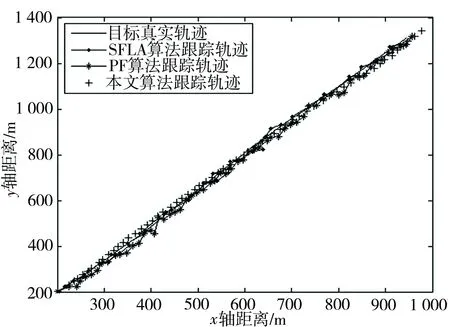
图1　不同算法的跟踪效果对比

图2为本文算法、SFLA算法和粒子滤波算法独立仿真的均方根误差仿真图，可以看出随着仿真次数的增加，本文算法跟踪性能较稳定，误差保持在很小的范围内波动，而SFLA算法和粒子滤波算法的误差波动相对较大，且始终大于本文算法的跟踪均方误差，也充分说明了本文改进算法有效利用了蛙跳算法的很多优点，克服了粒子滤波算法中粒子退化现象等很多缺陷，表现出很好的跟踪效果。

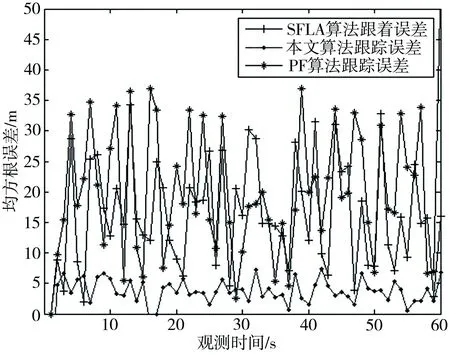
图2　不同跟踪算法的均方根误差比较

算法的性能分析，从图1、图2可以看出， SFLA算法的跟踪效果略优于粒子滤波算法，因为SFLA算法具有良好的蛙群更新机制，保持了蛙种类的多样性，进而在跟踪性能上较稳定，而粒子滤波算法本身的粒子更新机制较差，只保留了较好的粒子，导致种群内粒子多样性缺失，进而导致跟踪效果变差。而本文的改进算法恰好结合了两个算法的优点，抑制了粒子的退化，从而保持了粒子的多样性，所以跟踪效果稳定而精确。同时，本文改进算法省去了粒子重采样的步骤，大大降低了算法的复杂度。

3结论

综上所述，本文提出了基于改进SFLA-PF算法的目标跟踪技术，利用蛙跳算法的高效计算能力和优良的全局搜索能力，以及很好的信息交互和协作能力。把它引入到粒子滤波算法中，使其粒子群体也表现出复杂的智能效果，从实验结果看这种改进很好地抑制了粒子陷入局部最优和退化现象，同时也验证了该算法能够精确地进行动态目标跟踪。

参考文献：

[1]PAULINER.Isaglobalsystemofinternationallarge-scaleassessmentsnecessaryfortrackingprogressofapost-2015learningtarget?[J].Compare:ajournalofcomparativeandinternationaleducation，2015，45(3)：486-490.

[2]宋策. 基于粒子滤波的目标跟踪技术研究[D].长春：长春光学精密机械与物理研究所，2014.

[3]朱良谊，王庆. 一种基于粒子滤波的优化目标跟踪算法研究[J].西北工业大学学报，2013(6)：967-973.

[4]蒋鹏,宋华华,林广. 基于粒子群优化和M-H抽样粒子滤波的传感器网络目标跟踪方法[J].通信学报，2013(11)：8-17.

[5]马勤. 基于群体智能算法的动态目标跟踪技术研究[D]. 天津：天津理工大学,2010.

[6]葛宇，王学平，梁静. 改进的混合蛙跳算法[J].计算机应用，2012(1)：234-237.

[7]DANILOP，MASSIMOT，PIERLUIGII.Improvingtheprofitabilityoftechnicalanalysisthroughintelligentalgorithms[J].Journalofinterdisciplinarymathematics，2013，16(2-03)：203-215.

[8]张友华.混合蛙跳算法的改进及其应用研究[D].兰州：甘肃农业大学，2013.

[9]李晶晶,戴月明. 自适应混合变异的蛙跳算法[J]. 计算机工程与应用，2013(10)：58-61.

[10]蔡荣太,吴元昊,王明佳,等.视频目标跟踪算法综述[J].电视技术，2010，34(12)：135-138.

[11]THANGNV，TRINHCD，TRANDT.ApplicationofstreettrackingalgorithminanINS/GPSintegratednavigationsystem[J].IEEEjournalofresearch，2015，61(3)：1-9.

[12]蒋巍,张健,曾浩. 基于智能视频监控系统的运动目标检测和跟踪[J].电视技术，2012，36(5)：110-114.

[13]张彤,马延柯,首照宇.一种改进的Mean-Shift实时车辆跟踪算法[J].电视技术，2015，39(17)：126-130.

Improved tracking targets SFLA-PF algorithm based on OFDM system

CAO Xiangdong，MAO Yongyi

(SchoolofElectronicEngineering，Xi′anUniversityofPosts&Telecommunications，Xi′an710061，China)

Abstract:In the OFDM communication system, in order to solve nonlinear target tracking problem, an improved SFLA (SFLA) and particle filter (PF) is proposed based on a combination of methods to study the dynamic target tracking technology. Firstly, Gaussian mutation local search ability and Cauchy mutation global search ability, etc. are used to improve SFLA, then improved SFLA is used to optimize the dynamic tracking of particle filter algorithm, its advantages are not requiring resampling steps, and meanwhile effectively maintain the diversity and effectiveness of the particles. The simulation results show that the algorithm can effectively achieve dynamic target tracking, and tracking better than SFLA and particle filter algorithm under the same conditions.

Key words:OFDM；SFLA；particle filter；Gaussian mutation；Cauchy mutation

中图分类号:TN929.53

文献标志码：A

DOI：10.16280/j.videoe.2016.03.022

基金项目：陕西省自然科学基金项目(2014JM2-6088)

作者简介：

曹向东(1988— )，硕士，主研移动台定位跟踪技术；

毛永毅(1969— )，博士，教授，主研通信信号处理、移动台定位跟踪技术。

责任编辑：许盈

收稿日期：2015-11-26

文献引用格式：曹向东，毛永毅.基于改进SFLA-PF算法的OFDM系统目标跟踪[J].电视技术，2016，40(3)：103-106.

CAO X D，MAO Y Y. Improved tracking targets SFLA-PF algorithm based on OFDM system [J].Video engineering，2016，40(3)：103-106.