基于环形核的旋转不变性特征提取方法

王　迪，陈岳林，蔡晓东，吕　璐

(桂林电子科技大学 机械工程学院，广西　桂林　541004)

基于环形核的旋转不变性特征提取方法

王迪，陈岳林，蔡晓东，吕璐

(桂林电子科技大学 机械工程学院，广西桂林541004)

摘要:针对人脸在XOZ平面内旋转，即在图像所在平面内人脸产生的旋转，因特征值变化大导致人脸识别率降低的问题，提出了一种新颖的基于环形核的旋转不变性特征(Circular Kernel Feature，CKF)提取方法。所提算法有两个创新点，第一点是给出了环形核的建立方式，定位人脸上明显的特征部分。第二点是提供了特征的旋转不变计算方式。首先建立环形核，定位人脸上明显特征的坐标区域；然后，用旋转不变的计算方式获取定位区域的特征值。在Georgia Tech人脸数据库上的实验证明：人脸旋转前后CKF的值相较Gabor，LBP等特征值的变化小了98%。

关键词:CKF；旋转不变；环形核

1人脸识别

人脸识别常以比较人脸特征向量的方式衡量相似度，特征向量由特征值计算方式以及特征点定位两部分构成。人脸识别的难点在于人脸发生旋转的前后，人脸上相同位置的特征值发生了改变，导致同一个人脸旋转前后特征向量不同，相似度降低，识别不出是同一个人。基于解决这个问题，有提出放射变换和透视原理的人脸多紫台矫正方法，利用改变图像比例，旋转角度来矫正旋转后的人脸，但是这种方法只针对旋转小于±45°的人脸有效[1]。还有的人脸检测中将检测到的区域颜色信息特征向量作为人脸特征，这种算法过分依赖人脸检测准确率而且耗费时间较长[2]。也有一些算法采用广义旋转不变性核函数，可以大幅提高抗噪能力，但是搭建过程复杂，识别率受参数影响较大，容易过拟合[3]。

本文提出了一种旋转不变特征，首先由ASM[4]定位到人脸的鼻尖点，以此为旋转中心；其次，标定所需的人脸特征极坐标，每个特征点坐标由半径和角度两个参数决定；最后求该坐标附近3×3区域的像素均值作为该坐标点的特征值。由此得到的特征向量依然会随人脸旋转发生改变，因此半径相同的坐标点的特征值要按从小到大的顺序存放入特征向量。这样即使人脸在XOZ平面内旋转，特征向量也不会发生变化。

2CKF特征提取

提取CKF需要构建一个环形核保存特征点的特征值，特征点由半径和角度两个参数决定，半径相同的特征点作为一环存入一个特征向量。人脸上所有点之间的距离不会随人脸旋转发生变化，因此当确定一个旋转中心后，任一定位到的特征点在人脸旋转前后都处在同一个环上。

2.1构建环形核

本文提出了一种CKF特征，它提取了人脸旋转不变性特征。

首先，为了构建环形核本文采用了ASM模型[5]定位出图像的鼻尖点，如图1所示第52号点作为旋转中心点。半径是由人脸上几处关键点位置[6]决定的，本文给出5个位置，均由ASM定位获取，它们分别到旋转中心的连线作为5个环的半径。如图1所示，5条连线即5个环的半径，这5个关键点由近及远依次为：人中顶部点(第56号点)、左鼻翼最左点(第58号点)、上嘴唇下沿中点(第67号点)、嘴巴左边角点(第59号点)、左眼瞳孔中心点(第38号点)。这些都是梯度较大点，特征信息较多，因此选这些点所在环的特征值作为人脸特征信息。

图1　ASM定位点图

其中，5条连线的交点即第52号点是旋转中心点；鲜红色连线的末端即人中顶部点(第56号点)；黄色连线的末端即左鼻翼最左点(第58号点)；绿色连线的末端即上嘴唇下沿中点(第67号点)；深红色连线的末端即嘴巴左边角点(第59号点)；黑色连线的末端即左眼瞳孔中心点(第38号点)。

任意特征点的角度是由该点的半径决定的，L(周长)=2×π×R，向下取整得到该特征点所在环的像素点个数，被360°整除，得到该环上每个特征点的角度间隔，即人脸上每环像素点极坐标确定了，如图2所示。

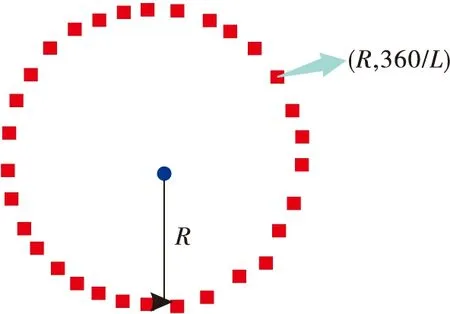
图2　每一环的角度分布图

L=2×PI×R，N=[360/L]

(1)

式中：L表示一环有L个像素点；“[ ]”表示向下取整；N表示一环有N个特征点。

2.2计算旋转不变性特征值

算法流程如下：

1)for i=0，…，num_ring

2)for j=0，…，num_pixes

计算每个像素点的局部均值作为该点的像素值；

存入pixes[num_pixes]数组；

3)endfor；

4)for m=0，…num_pixes-1

5)for n=m+1，…，num_pixes

6)if pixes[n]

temp=pixes[n]；

pixes[n]=pixes[m]；

pixes[m]=temp；

7)end if；

8)end for；

9)end for；

10)end；

其中：num_ring表示总环数；num_pixes表示每环的特征点个数；pixes[num_pixes]表示每环存放特征点的数组。具体计算过程如下。

搭建好环形核，在这些极坐标处计算特征值并按序存放。首先，将每个极坐标转换为人脸图像上的直角坐标，在每个特征点3×3邻域计算像素均值，作为该特征点的特征值，目的是降低定位带来的误差，取定位到的特征点的特征模糊值，如图3所示。

X=(a1+a2+a3+a4+a5+a6+a7+a8)/8

(2)

图3　特征模糊值计算图

式中：S={a1，a2，a3，a4，a5，a6，a7，a8}表示某像素点X的周围8个像素点的集合；ai(i≤8)表示第i个像素点的像素值。

每环的全部特征值要按从小到大的顺序依次存入一个特征向量，因为人脸发生旋转前后，任一特征点都在同一个环上，但是在环上的位置会发生变化。因此CKF在保存特征值的时候是按序存放，即使人脸发生旋转，特征向量中的特征值顺序不发生变化。旋转前后的人脸图像对比每环特征向量都大致相同，如图4所示，即CKF是旋转不变的特征。

图4　旋转不变性计算图

算法流程如下：

1)for m=0,…num_pixes-1

2)for n=m+1,…,num_pixes

3)if pixes[n]

temp=pixes[n];

pixes[n]=pixes[m];

pixes[m]=temp;

4)end if;

5)end for;

6)end for;

其中，num_pixes 表示每环有num_pixes个特征点，pixes[num_pixes]表示每环的特征点都存放这个数组，将每环的特征点按特征从小到大的顺序存放。因此旋转前后同一环上的pixes[num_pixes]的值是相同的。由图4可以看出，旋转前后人脸的CKF相同，即CKF的旋转不变性。

3实验及结果分析

3.1实验目标及过程

实验采用Georgia Tech人脸数据库50人，每人15张不同姿态的人脸图像，共计750张。使用该人脸数据库原因如下：1)每个人都有多张XOZ平面内的旋转图像；2)背景干扰小；3)像素足够清晰。

实验阶段将每个人的正脸和在XOZ平面内发生旋转的图像取出。以单个人为例，提取正脸的CKF和一个旋转后人脸的CKF，如图5部分样本所示。旋转前后的人脸都用一个CKF构成的特征向量表示，图5a是旋转前的正脸，图5b是旋转后的脸。计算一个人的旋转前后图像的特征向量的欧氏距离。同理提取人脸的Gabor[7]和LBP[8]特征，结论见图6所示。

图5　人脸数据库

图6　不同算法提取的特征向量欧氏距离对比图

3.2实验结果与分析

实验结果如图6所示，其中提取的是Georgia Tech人脸数据库中750张图像的CFK作为特征向量，比较旋转前后两图像特征向量的的欧氏距离，平均欧氏距离为400，而提取Gabor和LBP特征作为特征向量，旋转前后图像的平均欧氏距离达到了20 000以上。因此实验证明：CFK特征较Gabor，LBP这类传统特征具有较强的旋转不变性。

4结束语

本文提取人脸的CKF特征，该特征：1)建立的环形核，核内特征值不会随人脸旋转而发生改变；2)在ASM定位准确时，由实验数据可知CKF相比Gabor和LBP两种特征，对于人脸旋转更具有鲁棒性，可推广到人脸识别应用领域。未来进一步的研究方向是在其他平面内改进CKF，最终实现CKF适用于人脸的各种姿态变化。

参考文献：

[1]GUO B F，LAM K M，LIN K H，et al.Human face recognition based on spatially weighted Hausdorff distance[J].Pattern recognition letters，2003，24(3)：499-507.

[2]祝磊，朱善安.人脸识别的一种新的特征提取方法[J].光电工程，2007，34(6)：122-125.

[3]HAMSICIONUR C. Rotation invariant kernels and their application to shape analysis[J].IEEE transactions on pattern analysis and machine intelligence，2009，31(11)：1985-1999.

[4]LI D，KONG F. Facial feature point extraction using a new improve active shape model[J].International congress on image & signal processing,2010(2)：944-948.

[5]MILBORROW S，MORKEL J，NICOLLS F. The MUCT landmarked face database[EB/OL].[2015-08-24]. https://www.researchgate.net/publication/264885609_The_MUCT_Landmarked_Face_Database.

[6]MILBORROW S，NICOLLS F. Active shape models with SIFT descriptors and MARS[EB/OL].[2015-08-24].http://xueshu.baidu.com/s?wd=paperuri%3A%285a8b47ec4e9b9f94367f00bfa93f45c0%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdx.doi.org%2F10.5220%2F0004680003800387&ie=utf-8.

[7]王庆军，张汝波.基于Log-Gabor和正交等度规映射的人脸识别[J].计算机科学，2011，38(2)：274-276.

[8]王映辉. 人脸识别—原理、方法与技术[M].北京：科学出版社，2010.

王迪(1988— )，硕士生，主研智能视频分析与人脸识别；

陈岳林(1968— )，硕士生导师，主研机制、机电等；

蔡晓东(1971— )，硕士生导师，主研并行化图像和视频处理、模式识别与智能系统、基于云构架的智能传感器网络，为本文通讯作者；

吕璐(1992— )，硕士生，主研智能视频分析与人脸识别。

责任编辑：时雯

Feature extraction method based on CKF for face recognition

WANG Di，CHEN Yuelin，CAI Xiaodong，LÜ Lu

(SchoolofInformationandCommunication，GuilinUniversityofElectronicTechnology，GuangxiGuilin541004，China)

Abstract:A novel mechanism named CKF(Circular Kernel Feature) for solving the problem that face recognition rate reduced by rotation is proposed in this paper. Firstly， characteristics of rotation in-variants are defined. Then， to establish the annular nuclear，striking features are located. Secondly， eigenvalues by rotation invariant method are calculated . Experimental results show that， compared with traditional Gabor and LBP， the Euclidean distance of CKF achieved 98 percent reduction using Georgia Tech database.

Key words:CKF；rotation invariant；circular nucleus

中图分类号:TP391.4

文献标志码：A

DOI：10.16280/j.videoe.2016.03.001

基金项目：国家科技支撑计划课题项目(2014BAK11B02)；广西科学研究与技术开发计划项目(桂科攻14122007-5)；广西自然科学基金项目(2013GXNSFAA019326)

作者简介：

收稿日期：2015-08-24

文献引用格式：王迪，陈岳林，蔡晓东，等.基于环形核的旋转不变性特征提取方法[J].电视技术,2016，40(3)：1-4.

WANG D，CHEN Y L，CAI X D，et al.Feature extraction method based on CKF for face recognition [J].Video engineering,2016,40(3)：1-4.