融合多源数据的局部重力场建模中线性化误差的研究

吴怿昊　罗志才,2

1　武汉大学测绘学院，武汉市珞喻路129号，430079 2　武汉大学地球空间环境与大地测量教育部重点实验室，武汉市珞喻路129号，430079



融合多源数据的局部重力场建模中线性化误差的研究

吴怿昊1罗志才1,2

1武汉大学测绘学院，武汉市珞喻路129号，430079 2武汉大学地球空间环境与大地测量教育部重点实验室，武汉市珞喻路129号，430079

摘要：引入高阶重力场模型作为参考场，削弱局部重力场逼近中线性化误差的影响。以实测的陆地重力异常、船载重力异常及航空重力扰动为基础数据，基于泊松小波径向基函数分析不同参考场对局部重力场逼近的影响。结果表明，引入高阶全球重力场模型代替GRS80参考椭球正常场作为参考场，能更为准确地逼近真实的重力场，有效削弱线性化误差的影响。相比于基于GRS80正常场构建的似大地水准面模型，基于DGM1S重力场模型为参考场构建的似大地水准面的精度，在地形起伏较大的德国、英国及挪威区域分别提高了1.5 mm、3.3 mm和9.0 mm。

关键词：局部重力场建模；线性化误差；泊松小波基函数；全球重力场模型

局部重力场建模的研究往往归结为对扰动位的研究，即从重力位中移去由参考椭球代表的正常重力位得到的差值[1]。基于此，重力观测值需移去正常重力值并经过相应的归算后应用于局部重力场的解算，但此过程会不可避免地引入相应的线性化误差[2]。Heck[3]的研究表明，上述线性化的误差可能分别对于重力异常/扰动和高程异常产生mGal级和cm级以上的误差。Denker[4]提出使用高阶全球重力场模型作为参考重力场，以削弱线性化误差的影响，并进行了相关理论推导。上述研究表明，在高精度的局部重力场建模中需考虑线性化误差的影响。然而如何基于全球重力场模型为参考场，研究融合多源数据构建局部重力场模型的线性化误差，国内外未有相关成果发表。基于此，本文以泊松小波径向基函数(radial basis functions)为构造基函数[5-8]，基于部分欧洲地区的地面重力、船载重力及航空重力数据，以移去-恢复法为基本框架，分别利用全球重力场模型以及参考椭球确定的参考场构建相应的似大地水准面模型，分析全球重力场模型在削弱线性化误差中的应用。

1局部重力场建模方法

基于移去-恢复法，残余扰动位Tres可表示为有限个泊松小波基函数之和[7-8]：

(1)

式中，x为重力场观测数据的三维坐标，y为基函数的位置，K为基函数的个数，βi为基函数的未知参数，Ψ(x,yi)为泊松小波径向基函数，其具体形式可参考文献[7-8]。

多源重力场观测数据可表示为扰动位的泛函。本文利用航空重力扰动δg、陆地及船测重力异常Δg逼近局部重力场，其解算结果以似大地水准面即高程异常ζ显示。上述重力场的相关参量在球面近似条件下分别与扰动位存在如下函数关系[7]：

(2)

(3)

(4)

式中，γ为平均正常重力值。

结合式(1)，对某一类观测值可以建立如下观测方程[7]：

(5)

式中，Lp为第p类的重力场信息观测值，Δp为观测误差，fp为此类观测值与扰动位之间的泛函关系，J为观测数据种类的个数。将式(5)改写为误差方程的形式：

Vp=ApX-lp

(6)

式中，Ap为mp×K设计矩阵，X为K×1基函数的未知参数向量，lp为该观测类mp×1误差方程的常数项向量，Vp为mp×1观测值残差向量，mp为该类重力场观测值的个数。将各类观测值联合起来，总的误差方程可表示为：

V=AX-l

(7)

式中，

(8)

假定不同类型的观测值之间互不相关，观测数据的方差-协方差阵可以表示为：

(9)

利用最小二乘原理，基函数的未知参数向量X的估值可表示为：

(10)

式中，

(11)

(12)

为了对各类观测值进行合理的定权，采用方差分量估计的方法，即通过平差随机模型的验后估计方法重新估计各类观测值的单位权方差因子[9]：

(13)

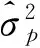
(14)

基于上述原理，重力观测数据需移去正常重力值并进行归算后应用于局部重力场的解算，而上述数据处理过程中不可避免地引入了相应的线性化误差[2]。

2基于高阶重力场模型的观测数据线性化模型

Denker[4]提出使用高阶全球重力场模型作为参考重力场，以削弱线性化误差的影响。基于Molodensky边值理论，假设P点为地球表面上的一点，Q点为相应于P点位于似地形表面上的点，则有[1]：

(15)

式中，φP和φQ分别为P点和Q点的纬度，λP和λQ分别为P点和Q点的经度，UQ为Q点的正常位，U0为参考椭球面的正常位，W0和WP分别为大地水准面和P点上的重力位。

P点扰动位TP为[1]：

TP=WP-UP

(16)

利用泰勒级数，将P点的正常位UP在Q点展开，忽略高阶项的影响[1]：

(17)

式中，γQ为Q点的正常重力。结合式(15)，P点的高程异常ζP可表示为[1]：

(18)

式(18)即为广义布隆斯公式。在球面近似的条件下，P点的重力扰动δg和重力异常Δg可表示为[1]：

(19)

(20)

式(17)中，利用参考椭球确定的正常重力场(通常为GRS80椭球确定的正常场)确定了P点与Q点正常重力位之间的关系，由于忽略了高阶项的影响，会引入相应的线性化误差。Heck[3]的研究表明，忽略高阶项带来的线性化误差对于重力异常/扰动的影响达到mGal级，对于高程异常的影响可达cm级。Denker[4]引入全球重力场模型作为参考场来削弱线性化误差的影响。此时，Q点的位置变化为全球重力场模型确定的似地形表面上，用Q*表示，则式(15)变为[4]：

(21)

相对于参考椭球确定的正常重力场，由全球重力场模型确定的参考场能更为准确地逼近真实的重力场。因此，较之于Q点，Q*点更接近于真实的地形表面。Q*点的椭球高hQ*可通过式(22)迭代计算[4]：

(22)

引入全球重力场为参考场后，P点的扰动位TP也相应变为T*P，则式(16)变为[4]：

(23)

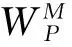
(24)

(25)

(26)

3数值计算与分析

3.1多源数据及预处理

收集覆盖整个荷兰、比利时、英国、部分德国、法国、丹麦、挪威和北海部分区域的多源重力观测数据。其中，陆地重力数据的精度约为1mGal，平均空间分辨率约为5km，见图1(a)；船载重力数据的精度约为2mGal，平均空间分辨率约为7km,见图1(b)；航空重力数据的精度约为2mGal，见图1(c)。通过交叉点平差的方法完成船载、航空重力数据中系统偏差的校正；利用阈值法和Hampel滤波剔除多源重力数据中存在的粗差；利用低通滤波削弱船载、航空重力数据中存在的高频噪声的影响，并将各类重力观测数据归算到同一参考框架(ETRS89)及垂直基准(EVRF2007)。重力场模型采用代尔夫特理工大学基于GRACE/GOCE联合解算的模型DGM1S，其球谐展开阶数达到250阶[10]。基于移去-恢复法，利用DGM1S模型移去全球重力场模型代表的重力场的长波信号，并基于残余地形模型(RTM)移去局部地形扰动引起的高频重力场信息[11]，计算得到的残余重力观测数据的统计信息见表1。同样，基于移去-恢复法移去由GPS水准数据确定的高程异常中的DGM1S模型以及RTM模型分别代表的低频和高频部分，图2显示了用于后续局部似大地水准面模型精度评价的GPS水准点上的残余高程异常。

3.2基于DGM1S为参考场构建的局部似大地水准面模型

基于上述多源重力数据，利用泊松小波基函数构建局部重力场模型，计算区域覆盖荷兰、比利时、英国以及部分挪威、德国、法国和北海区域。图3(a)表示基于DGM1S模型为参考重力场解算得到的残余似大地水准面，图3(b)表示分别利用DGM1S模型与GRS80椭球为参考场解算得到的似大地水准面的差距，其差距可达cm级且主要集中在挪威南部、英国及德国部分山脉地区。表2和表3分别给出了基于DGM1S模型与GRS80参考椭球正常场为参考场构建的似大地水准面的检核结果。基于两种参考场构建的似大地水准面在地势平坦的荷兰、比利时区域精度相当。而在地形起伏较大的德国、英国及挪威相关区域，前者精度分别比后者提高了1.5 mm、3.3 mm和9.0 mm。在多山区域，由于地形扰动的影响，由参考椭球确定的似地形表面与真实的地形表面差距较大，在数据归算时会产生较大的线性化误差。而利用DGM1S重力场模型代替GRS80正常场能够更为准确地逼近真实的重力场，减小线性化误差。

4结语

本文研究了局部重力场逼近中的线性化误差问题，引入高阶重力场模型作为参考重力场，从而削弱线性化误差的影响。利用泊松小波径向基函数为构造基函数，以实测的陆地重力异常、船载重力异常及航空重力扰动为基础数据，比较了不同参考场模型对于局部重力场逼近的影响。结果表明，在多山地区，基于GRS80参考椭球的正常重力场模型构建的似大地水准面可能引入cm级的线性化误差，而利用DGM1S重力场模型作为参考场更为接近真实的局部重力场，可以有效地削弱线性化误差的影响。在地形起伏较大的德国、英国及挪威相关区域，基于后者构建的似大地水准面的精度分别比前者提高了1.5 mm、3.3 mm和9.0 mm。

参考文献

[1]Moritz H. Advanced Physical Geodesy [M]. Karlsruhe:Abacus Press, 1980

[2]Heck B. On the Linearized Boundary Value Problems of Physical Geodesy [R]. Department of Geodetic Science and Surveying, OSU, 1991

[3]Heck B. Formulation and Linearization of Boundary Value Problems: From Observables to a Mathematical Model[A]//Lecture Notes in Earth Sciences[M]. Berlin:Springer, 1997

[4]Denker H. Regional Gravity Field Modeling: Theory and Practical Results [A]//Sciences of Geodesy[M]. Berlin:Springer, 2013

[5]Bentel K, Schmidt M, Gerlach C. Different Radial Basis Functions and Their Applicability for Regional Gravity Field Representation on the Sphere[J]. International Journal on Geomathematics, 2013, 4(1):67-96

[6]Bentel K, Schmidt M, Rolstad-Denby C. Artifacts in Regional Gravity Representations with Spherical Radial Basis Functions [J]. Journal of Geodetic Science, 2013, 3(3):173-187

[7]Klees R, Tenzer R, Prutkin I, et al. A Data-Driven Approach to Local Gravity Field Modelling Using Spherical Radial Basis Functions [J]. Journal of Geodesy, 2008, 82(8):457-471

[8]Tenzer R, Klees R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling [J]. Stud Geophys Geod, 2008, 52(3):287-304

[9]Kusche J. Noise Variance Estimation and Optimal Weight Determination for GOCE Gravity Recovery [J]. Advances in Geosciences, 2003, 1(1):81-85

[10]Hashemi F H, Ditmar P, Klees R, et al. The Static Gravity Field Model DGM1S from GRACE and GOCE Data: Computation, Validation and an Analysis of GOCE Mission’s Added Value [J]. Journal of Geodesy, 2013, 87(9):843-867

[11]Heck B, Seitz K. A Comparison of the Tesseroid, Prism and Point-Mass Approaches for Mass Reductions in Gravity Field Modeling [J]. Journal of Geodesy, 2007, 81(2):121-136

Foundation support:National Natural Science Foundation of China, No. 41374023.

About the first author:WU Yihao, PhD candidate, majors in physical geodesy, E-mail: whuwyh@126.com.

The Research on Linearization Errors in Regional Gravity Field Modeling Based on Heterogeneous Data Sets

WUYihao1LUOZhicai1,2

1School of Geodesy and Geomatics, Wuhan University,129 Luoyu Road, Wuhan 430079, China 2Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University,129 Luoyu Road, Wuhan 430079, China

Abstract:This paper studies the issues of linearization errors in regional gravity field modeling and introduces the high-order global gravity model as reference gravity field to reduce the corresponding linearization errors. As an example, we analyze the effects on regional gravity field modeling introduced by different reference gravity fields. To do so, we use Poisson wavelets radial basis functions based on terrestrial and shipboard gravity anomaly andon airborne gravity disturbance. The results show that the incorporation of global gravity field model, instead of GRS80-derived normal gravity field, as the reference gravity field leads a better approximation of the real gravity field. The corresponding linearization errors are also reduced. Compared to the quasi-geoid computed from the GRS80-derived normal gravity field, the accuracy of the quasi-geoid based on DGM1S-derived reference gravity field is improved by 1.5 mm, 3.3 mm and 9.0 mm at Germany, England and Norway respectively, where the topography show more undulation.Key words: regional gravity field modeling; linearization errors; Poisson wavelets radial basis function; global gravity field model

收稿日期：2015-10-11

第一作者简介：吴怿昊，博士生，主要从事物理大地测量学研究，E-mail: whuwyh@126.com。 通讯作者：罗志才，教授，博士生导师，主要从事物理大地测量学和卫星重力学研究，E-mail: zhcluo@sgg.whu.edu.cn。

DOI：10.14075/j.jgg.2016.06.002

文章编号：1671-5942(2016)06-0476-05

中图分类号：P223

文献标识码：A

Corresponding author:LUO Zhicai, professor, PhD supervisor, majors in physical geodesy and satellite gravity, E-mail: zhcluo@sgg.whu.edu.cn.

项目来源：国家自然科学基金 (41374023)。