大型摊铺机车架的力学特性分析与结构优化设计
2016-06-24晏腾飞张建润彭光强
晏腾飞 张建润 彭光强 王 浩
(1东南大学机械工程学院, 南京211189)(2徐工集团工程机械股份有限公司,徐州221000)
大型摊铺机车架的力学特性分析与结构优化设计
晏腾飞1张建润1彭光强2王浩2
(1东南大学机械工程学院, 南京211189)(2徐工集团工程机械股份有限公司,徐州221000)
摘要:首先,基于大型摊铺机车架刚度和强度设计方法,建立大型摊铺机车架的有限元模型.然后,通过模态仿真计算与模态分析得到车架的前10阶固有频率及主要振型,并通过模态实验验证了有限元模型的正确性.最后,提出动静力学特性相结合的综合结构设计方法:以动态刚度为目标函数,通过相对灵敏度分析确定车架刚度薄弱部分,利用拓扑优化手段实现摊铺机车架局部形状的改变及加强筋的布置,以提高车架刚度;结合静力学特性,分析摊铺机车架在静置情况下的应力分布及变形情况,以校验其性能可靠性,最终完成车架结构优化设计.对优化后的车架进行仿真分析,结果表明,优化后车架第1阶和第2阶固有频率明显提高,同时车架质量减少了3%.
关键词:车架;模态分析;灵敏度分析;拓扑优化
摊铺机作为专用的物料摊铺机械,其摊铺质量主要与熨平板、振捣机构、车架、找平系统、螺旋分料机构,以及这些系统之间的相互协调有关.其中,车架在摊铺机作业过程中,受到发动机、路面和熨平板振捣系统的激励,结构不合理的车架会产生非理想的振动,从而极大地影响摊铺质量.尤其对于大型摊铺机,其对精度和摊铺质量的要求更高,因而对大型摊铺机车架进行结构优化以提高其刚度具有重要意义.
近30年来,工程结构的优化设计受到工程技术人员的广泛关注,并已取得一定的进展.结构优化可分为3类:① 参数优化,其设计参数为结构的材料参数(如材料弹性模量、质量密度)、梁杆的截面参数(截面尺寸等)及板的厚度等;② 形状优化,将其几何边界坐标作为设计变量,来优化结构的形状;③ 拓扑优化,通过改变拓扑结构即质量分布达到结构优化设计的目的.与参数优化或形状优化相比,拓扑优化能更好地改进结构设计.
早期的工程结构优化设计主要考虑的是静力学特性,如变形及应力分布等.但随着工程技术的发展,在工程结构优化设计中,动力学性能的要求越来越突出,其对工程机械性能的影响也越来越大[1-3].
基于上述工程机械结构优化设计方法及理论的研究基础,本文以大型摊铺机车架为研究对象,应用动静力学特性相结合的设计方法,使用灵敏度分析和拓扑优化的结构设计手段,在满足摊铺机车架静力学性能的前提下,改进大型摊铺机车架的结构形式,改善其动力学特性,从而提升其摊铺作业质量.
1车架特性分析及有限元模型建立
应用摊铺机可加快施工进度、减少压路机的滚压遍数,提高铺筑路面的质量,因而摊铺机已经成为沥青等物料摊铺作业的专用机械[4].沥青混凝土摊铺机按照对路面的宽度、厚度、拱度、平整度、压实度等方面的要求,完成道路面层和基层的沥青等物料摊铺,并利用熨平装置初步捣实和熨平路面.本文所研究的大型摊铺机为履带式沥青混合料摊铺机,其基本结构如图1所示.
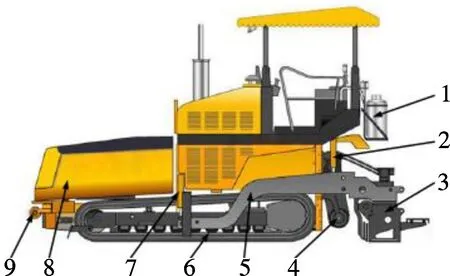
1—加热丙烷气罐;2—大臂液压油缸;3—熨平板;4—螺旋布料器;5—大臂;6—行走机构;7—调平系统液压油缸;8—料斗;9—顶推辊
摊铺机在作业时,通过顶推辊带动装有沥青混合料的工程车前进,混合料随着摊铺进程不断堆积在料斗内,并通过输料刮板将料斗内的混合料不断往后运送,螺旋布料器再将混合料均匀分布到熨平板横向各处,最终通过熨平板实现混合料的熨平和初步压实.摊铺机车架作为各零部件连接的基础,不合理的车架结构会极大地影响摊铺机作业的质量.因此,对大型摊铺机车架进行结构优化设计以提高其动力学性能非常重要.
为了提高有限元计算效率及精度,利用HyperWorks中的HyperMesh前处理器对摊铺机车架几何模型进行一定的简化处理,主要包括:
1) 删除并填充车架上直径小于20mm的用于连接的螺栓孔;
2) 删除车架上半径小于10mm的小的倒圆角;
3) 将实际中焊接的部分进行处理,使焊接的两部分相接触[5].
然后采用面网格和体网格相结合的方式对模型进行网格划分.网格单元数为357×104,节点数为101×104,大型摊铺机车架网格模型如图2所示.

图2 车架有限元模型
2车架模态仿真计算与分析
摊铺机车架作为整车系统中熨平板、振捣机构、找平系统及螺旋分料机构等的连接基础,其对摊铺质量的影响主要体现在其动力学特性.因此,本文以改善其动力学特性为目标,对摊铺机车架进行模态仿真,分析其固有频率及振型,以期在后续设计中使固有频率避开激励频率.
对划分好网格的车架模型设置材料(Q345钢)属性:密度、弹性模量、泊松比.采用自由边界条件,不施加任何约束,进行模态仿真分析.由于自由边界条件下前6阶模态为刚体模态,对应的模态固有频率基本为零,因此用兰索斯法提取车架除刚体模态外的前10阶模态.其固有频率及振型描述如表1所示,各阶模态振型如图3所示.

表1 各阶模态固有频率及振型描述

(a) 第1阶
(b) 第2阶

(c) 第3阶

(e) 第5阶

(g) 第7阶

(i) 第9阶
由仿真计算结果可看出,车架第1阶模态振型为左右方向的扭转弯曲,固有频率为13.8Hz;第2阶模态振型为扭转弯曲振动,固有频率为28.6Hz;第3阶模态振型为前后弯曲振动,固有频率为 29.5Hz.
3车架模态实验
在摊铺机车架有限元仿真过程中,为了提高网格质量,缩短计算时间,提高计算精度,对模型进行了一定的简化处理.为验证这些简化处理是否合理,本文对车架开展了模态实验.实验采用单点激励、多点拾振的模态测试原理,用桁车将车架吊起使其处于自由状态,在车架一侧选择激励点,通过敲击激励点获得其他各点的响应.根据模态实验结果,车架在100Hz频段内共激励出3阶模态.其固有频率如表2所示,振型如图4所示.

表2 车架模态实验固有频率 Hz

(a) 第1阶振型

(b) 第2阶振型

(c) 第3阶振型
实验得到的车架前3阶振型分别对应仿真结果的第2阶、7阶和10阶振型,实验结果与仿真结果的对比见表3.由表可知,实验与仿真得到的固有频率相对误差最高为4.6%.
表3车架模态实验与有限元计算结果对比

阶数固有频率/Hz实验值仿真值相对误差/%129.628.63.4243.741.74.6353.553.90.7
为了进一步验证仿真与实验所得振型的一致性,选取车架两侧板前中后6个特征点,如图4(c)所示.以特征点1为参考点,分别读取其他各点在3个坐标方向相对于特征点1的位移值,并与仿真结果进行对比验证.
图5为摊铺机车架仿真与模态实验振型对比图.在各特征点位置,仿真计算的振型与实验所得振型基本一致,进一步验证了有限元模型的正确性.同时通过仿真结果和实验结果的分析发现,车架模态仿真结果在车架与熨平板连接处因车架发生扭转和弯曲而引起的变形较大,且实验所得第1阶固有频率明显偏低,在实际作业过程中会影响其摊铺质量,因此可以通过改进结构来提高其固有频率,从而增加其结构刚度.

(a) 仿真第2阶和实验第1阶振型对比

(b) 仿真第7阶和实验第2阶振型对比

(c) 仿真第10阶和实验第3阶振型对比
4车架刚度灵敏度分析
通过前面车架模态的仿真和实验可以发现,摊铺机车架在与熨平板连接的部分刚度较弱,主要体现在前4阶振型在这些地方振动幅值较大,需要通过优化设计提高连接部分刚度性能.为得到车架本身关键零部件对其本身刚度影响的大小,首先对车架进行灵敏度分析[6-8].
该灵敏度分析以车架本身关键零部件的厚度为尺寸设计变量,以车架本身的自由模态的固有频率为约束条件,以车架整体质量最小为优化目标.所设计的各个零部件厚度参数如表4所示.
通过尺寸优化计算,可以得到车架本身质量和各阶固有频率相对于各尺寸设计变量的灵敏度.由于各个零部件大小差异较大,故取固有频率的灵敏度与车架本身质量灵敏度的比值(即相对灵敏度)来评价各零部件对车架本身刚度影响的大小.取车架模态实验的第1阶和第2阶固有频率(即对应仿真计算的第2阶和第7阶固有频率)为约束条件,可得到第1阶和第2阶固有频率相对于各个零部件厚度尺寸的相对灵敏度值,如图6所示.

表4 车架零部件厚度设计变量 mm

图6 第1阶和第2阶固有频率的相对灵敏度值
由图6可知,车架第1阶和第2阶固有频率相对于车架结构中的后挡板加强筋1、两侧板、两侧上部前后横梁、前挡板及外侧撑杆等的相对灵敏度值较大,这些结构对车架刚度影响较大.在后续设计中主要对这些结构进行优化设计.
5车架结构拓扑优化
拓扑优化是指在给定的设计空间找到最佳的材料分布或传力路径,以期在满足各种性能条件下实现轻量化设计的一种设计方法.密度法(SIMP)作为拓扑优化中一种常用的材料插值模型方法,其基本思路就是将有限元模型设计空间的每个单元的“单元密度”作为设计变量.该“单元密度”同结构的材料参数有关(单元密度与材料弹性模量E之间具有某种函数关系),在0~1之间连续取值,优化求解后单元密度为1(或接近1)表示该单元位置处的材料很重要,需要保留;单元密度为0(或接近0)表示该单元处材料不重要,可以去除,从而达到材料的高效利用,实现轻量化设计[9-10].
由第4节分析可知,车架结构中的两侧板、两侧上部前后横梁、前挡板及外侧撑杆对其刚度影响较大,需对它们进行拓扑优化.本文通过改变局部结构形状及使用加强筋来提高车架刚度.
拓扑优化数学模型可表述为
minf(X)=f(x1,x2,…,xn)
s.t.gj(X)≤0j=1,2,…,mg
hk(X)≤0k=1,2,…,mh

摊铺机车架结构拓扑优化以模型的材料密度为设计变量,以体积最小为目标函数,约束条件为:仿真模态的第1阶固有频率大于17Hz,第2阶固有频率大于35Hz,第3阶固有频率大于37Hz.通过拓扑优化得到车架关键零部件的基于密度的分布云图(见图7).

图7 车架关键零部件拓扑优化后密度云图
由图7可看出,在图中密度值较大的区域设置加强筋可显著提高车架第1阶和第2阶固有频率.结合相关的工艺基础,提出摊铺机车架改进方案,并对优化后的车架进行模态仿真计算,得到车架固有频率和振型.车架优化后第1阶和第2阶固有频率显著提高,且优化后的模型质量比优化前减少3%,约为155kg,符合设计要求.大型摊铺机车架优化前后固有频率的比较如表5所示.
表5车架优化前后固有频率比较

阶数固有频率/Hz优化前优化后变化率/%128.635.624.5241.744.56.7
6车架静力学性能校核
摊铺机车架在实际工作中不仅要满足动力学性能要求,而且要满足静力学性能要求,如静置条件下车架的局部应力分布是否合理以及变形情况是否在设计范围之内.为校验改进后的结构能否满足静力学性能要求,对车架进行静力学仿真分析.将动力总成系统作为集中质量点与车架刚性连接在一起,并将熨平板作为一个简化的整体与车架固连起来,熨平板为离地悬空状态,通过仿真得到静置条件下车架应力分布及变形情况(见图8和图9).

(a) 改进前

(b) 改进后

(a)改进前

(b) 改进后
分析图8和图9可知,改进前后车架在静置情况下,最大应力、最大变形均出现在车架后挡板与熨平板连接处.改进前最大应力为152MPa,改进后最大应力为140MPa,比改进前降低了8%,且在Q345钢的许用应力范围内;改进前最大变形量为2.69mm,改进后最大变形量为2.37mm,比改进前减少了12%,对熨平板本身的振动特性影响较小.综合上述分析可知,本文的优化模型符合设计要求.
7结论
1) 建立了大型摊铺机车架的有限元模型,并对其进行模态分析,同时通过模态实验验证了有限元模型的正确性.
2) 为了提高车架刚度,通过动静力学特性相结合的综合结构设计方法,利用灵敏度分析和拓扑优化手段,完成大型摊铺机车架结构的优化设计.
3) 在综合考虑大型摊铺机车架动力学及静力学特性的基础上,提出合理的结构件厚度分布及加强筋安装位置方案.改进后的车架第1阶和第2阶固有频率明显提高,动力学性能极大提升,且车架整体质量减少了3%,同时其静力学性能满足设计要求.
参考文献 (References)
[1]RoyR,HindujaS,TetiR.Recentadvancesinengineeringdesignoptimisation:Challengesandfuturetrends[J].CIRP Annals—Manufacturing Technology, 2008, 57(2):697-715.DOI:10.1016/j.cirp.2008.09.007.
[2]DaltonSK,AtamturkturS,FarajpourI,etal.Anoptimizationbasedapproachforstructuraldesignconsideringsafety,robustness,andcost[J]. Engineering Structures, 2013,57:356-363.
[3]扶原放, 金达锋, 乔蔚炜. 微型电动车车架结构优化设计方法[J]. 机械工程学报,2009,45(9):210-213.DOI:10.3901/JME.2009.09.210.
FuYuanfang,JinDafeng,QiaoWeiwei.Framestructureoptimizationdesignmethodforminiatureelectricvehicle[J]. Journal of Mechanical Engineering, 2009,45(9):210-213.DOI:10.3901/JME.2009.09.210. (inChinese)
[4]NguyenDH,BoutouilM,SebaibiN,etal.Valorizationofseashellby-productsinperviousconcretepavers[J].Construction and Building Materials, 2013, 49:151-160.DOI:10.1016/j.conbuildmat.2013.08.017.
[5]王钰栋, 金磊, 洪清泉, 等.HyperMesh&HyperView应用技巧与高级实例[M]. 北京: 机械工业出版社, 2013: 48-65.
[6]SakundariniN,TahaZ,Abdul-RashidSH,etal.Optimalmulti-materialselectionforlightweightdesignofautomotivebodyassemblyincorporatingrecyclability[J]. Materials & Design, 2013, 50:846-857.DOI:10.1016/j.matdes.2013.03.085.
[7]ParisJ,NavarrinaF,ColominasI,etal.Stressconstraintssensitivityanalysisinstructuraltopologyoptimization[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(33/34/35/36):2110-2122.DOI:10.1016/j.cma.2010.03.010.
[8]CaoW,QuLA.Astudyonthemassoptimizationofbusbodybasedonsensitivityanalysis[J].Automotive Engineering,2009,31(3):278-281.
[9]RoberM,TodtermuschkeM.Multiobjectivetopologyoptimizationoftrussstructuresforassemblydevicesusingintelligentswarmtechniques[J]. Procedia CIRP, 2014, 23:241-245.DOI:10.1016/j.procir.2014.10.083.
[10]JamesKA,LeeE,MartinsJRRA.Stress-basedtopologyoptimizationusinganisoparametriclevelsetmethod[J]. Finite Elements in Analysis and Design, 2012, 58:20-30.DOI:10.1016/j.finel.2012.03.012.
Analysisofmechanicalcharacteristicsandstructuraloptimizationdesignoflargepaverframe
YanTengfei1ZhangJianrun1PengGuangqiang2WangHao2
(1SchoolofMechanicalEngineering,SoutheastUniversity,Nanjing211189,China) (2XCMGConstructionMachineryCo.,Ltd.,Xuzhou221000,China)
Abstract:The finite element model of the large paver frame is established according to the stiffness and strength design method of it. The first 10 order natural frequencies and main vibration types of the paver frame are obtained through modal simulation calculation and modal analysis. And, the finite element model is verified to be reliable through the frame modal experiment. An integrated structure design method combining dynamic and static mechanical properties is proposed. The weak part of the frame stiffness is obtained by structure sensitivity analysis with dynamic stiffness as structural optimization’s objective. The frame stiffness is increased through the change of local shape and the arrangement of the reinforcing bars achieved by topology optimization. Based on the static analysis, the stress distribution and deformation of the frame in the static condition are analyzed to check the performance and reliability of the frame. Finally, the structural optimization design of the large paver frame is completed. The optimized frame is analyzed. The results show that the first and second order natural frequencies of the frame are improved obviously, and the frame mass is reduced by 3%.
Key words:frame; modal analysis; sensitivity analysis; topology optimization
doi:10.3969/j.issn.1001-0505.2016.03.005
收稿日期:2015-08-20.
作者简介:晏腾飞(1990—),男,硕士生;张建润(联系人),男,博士,教授,博士生导师,zhangjr@seu.edu.cn.
基金项目:江苏省科技支撑计划资助项目(BE2014133)、江苏省前瞻性联合研究资助项目(BY2014127-01).
中图分类号:U415.52
文献标志码:A
文章编号:1001-0505(2016)03-0483-06
引用本文: 晏腾飞,张建润,彭光强,等.大型摊铺机车架的力学特性分析与结构优化设计[J].东南大学学报:自然科学版,2016,46(3):483-488. [doi:10.3969/j.issn.1001-0505.2016.03.005].
