融入全局信息的局部拟合的活动轮廓模型

吴宜平，沈 明

(福州大学数学与计算机科学学院，福建 福州　350116)

融入全局信息的局部拟合的活动轮廓模型

吴宜平，沈 明

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：提出一种结合局部和全局灰度信息的图像分割模型. 该模型通过引入新的控制参数，降低了局部拟合项在局部二值拟合的活动轮廓模型(LBF模型)中的主导作用，同时增加了全局信息在模型中的辅助作用，从而改进了局部二元拟合项. 实验结果表明，改进的模型不仅能分割灰度不均的图像，而且提高了轮廓初始化的灵活性. 针对一些合成和真实的图像，改进的模型减轻了对轮廓初始化位置、 大小及噪声的敏感性，同时加快了曲线的演化速度，减少了CPU时间.

关键词：图像分割； 活动轮廓； 局部拟合； 偏微分方程； 灰度不均

0引言

图像分割[1]是图像理解和分析、 模式识别、 计算机视觉的关键步骤，被广泛应用于交通控制体系、 医学影像分析、 生物特征识别、 遥感等领域，因而受到国内外学者的广泛关注. 随着与数学理论的交叉研究和计算机处理能力的提高，基于偏微分方程的几何活动轮廓模型[2]已成为图像分割领域中热门的研究课题.

现有的几何活动轮廓模型通常可以划分为基于边缘和基于区域的两种模型. 活动轮廓[3](CV模型)是一个著名的基于区域的几何活动轮廓模型，该模型可以分割没有明显边缘或者缺乏明显纹理的图像，并且具有计算复杂性低，对初始曲线的位置不敏感，较好的抗噪性等优点，但模型需要周期性地重新初始化水平集函数以保证数值计算的稳定，而且不能处理目标灰度不均匀或者背景灰度不均匀的图像.

近几年来，为了解决灰度不均图像的分割问题，许多学者提出了不同的活动轮廓模型，例如： 李春明等[4]提出了把CV模型的全局二值拟合能量泛函改为以高斯函数为权重的可变区域拟合能量函数定义的局部拟合的活动轮廓模型(LBF模型)，该模型较好地克服了CV模型不能分割灰度不均图像的缺点，然而LBF模型的分割结果却严重依赖于演化曲线的大小和初始位置，并对噪声较为敏感； 戚世乐等[5]利用图像的局部信息快速为图像的目标大致定位，并结合LBF模型提出“两阶段”的活动轮廓模型，该模型改善了对轮廓初始化的敏感性，但需要分阶段实现，使算法的复杂度提高； 刘瑞娟等[6]结合改进CV模型[7]的全局灰度拟合力和局部图像拟合模型[8]的局部灰度拟合力，提出一种融合局部和全局图像信息的活动轮廓模型，该模型同样能减轻对轮廓初始化的敏感性，但在分割血管图像时演化速度慢； 王利等[9]提出一个基于CV模型与LBF模型的能量泛函线性组合的LGIF模型，该模型在灰度不均的医疗图像分割中取得了良好的效果，但未对初始曲线大小的敏感性和抗噪性问题进行研究.

受LGIF模型的启发, 提出一个新的ILBF模型，该模型通过控制参数的调节，降低了LBF模型中局部信息所起的作用，增加了一定权重的全局信息. 通过全局信息和局部信息的共同引导，新模型不但能够分割灰度不均图像，而且具有对初始曲线的大小和位置不敏感以及抗噪性强的优点.

1相关背景

1.1CV模型

CV模型的能量泛函定义为：

(1)

其中： μ≥0; λ1, λ2>0是固定的正常数； c1和c2分别为图像在演化曲线的内部和外部区域的平均灰度值. 固定水平集函数φ，相对于c1和c2最小化能量泛函(1)可得：

(2)

可见c1和c2没有包含任何的局部信息，当图像呈现灰度不均时, 用c1和c2分别近似图像在演化曲线内外的灰度值必会产生较大的误差，从而导致CV模型不能分割非同质图像.

1.2LBF模型

对图像中每一点x，LBF模型的能量泛函定义为：

(3)

其中： λ1, λ2, μ和v是正参数； K(x-y)为权重核函数； f1和f2为图像在点x处的两个局部拟合值. 固定水平集函数▽，极小化LBF模型的能量泛函(3)，可得：

(4)

该模型利用了图像的局部信息f1和f2，从而克服了灰度不均对图像分割造成的影响. 但是由于只考虑了图像像素点之间的空间信息而没有考虑其灰度变化信息，这种能量泛函的局部化特性使模型易于陷入局部极值，导致模型对轮廓初始化以及噪声十分敏感.

2新模型

2.1能量泛函的构建

LBF模型中选取权重函数为高斯核函数[10]：

(5)

其中:σ为参数. 由式(5)可知该函数具有单调性、 对称性等显著的几何特征, 高斯函数做权重完全以距离做为衡量的依据，使得邻域内的点对拟合能量做主要贡献. 因此，如果距离当前点x最近的点是噪声点，那么噪声点的权重很大，就会使局部拟合项失真，偏离实际情况. 另外一方面，由于未考虑像素间的相似性或者差异性等像素自身的特点，这样也会导致模型对轮廓初始化十分敏感. 由上述分析可知，高斯函数做权重会导致模型对轮廓初始化及噪声的敏感性.

为了降低局部拟合项的作用，增加真实的全局信息，对于图像I中的每一点x，提出新的局部能量泛函：

(6)

其中：λ1,λ2>0为正常数；ci,i=1, 2, 由公式(2)给出；fi,i=1, 2, 由公式(4)给出；w为控制参数，w∈(0, 1). 通过控制参数的调节，一方面可以降低局部拟合项的作用，避免因局部拟合项起主要作用而陷入局部极小值，而误分割出噪点； 另一方面也增加CV模型中真实的全局信息ci，由CV模型的优点可知，在全局信息的引导下可以加快轮廓线的演化，迅速收缩或者扩张到目标边界上，并且对轮廓初始化不敏感.

为了找到整幅图像中物体的目标边界，从局部意义上定义的能量泛函必须扩展到全局区域Ω上的能量泛函：

(7)

称该能量泛函为外部能量项或者保真项，用来确保拟合的图像尽可能地接近真实的图像. 引入Heaviside函数，用水平集函数φ的零水平集来表示闭合曲线C，并规定φ在C的内部区域取正，在C的外部区域取负值，在C上时取值为零，则用水平集方法表示的能量泛函为:

(8)

为了避免水平集函数演化过程中的反复初始化，要求水平集函数尽可能不偏离符号距离函数，添加李春明等[11-12]提出的二次惩罚项：

(9)

该惩罚项能够保证在数值求解过程中有稳态解[13]. 同时正则化演化曲线，添加弧长项[14]：

(10)

该弧长项可以在一定程度上控制过分割甚至误分割产生的冗余轮廓，保持曲线在演化过程中尽可能的短而且光滑.

综上所述，ILBF模型总的能量泛函为：

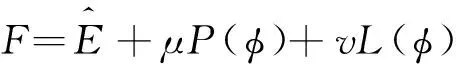
(11)

式中：μ,v>0 为权重参数； 参数μ控制二次惩罚项，同时由文献[11]可知，μ与迭代时间步长t必须满足μt<0.25； 参数ν用来调节演化曲线长度项，其值大小一般取决于待分割的目标物体的边界大小. 计算机实现水平集函数迭代演化时，Heaviside函数H和其导数Dirac函数δ是不可微函数，因此需要寻找光滑可微的函数来替代它们, 一般取光滑规则函数Hε近似Heaviside函数H，Hε定义为：

(12)

对其求导得光滑可导的Dirac函数δε

(13)

这里ε为正常数，不失一般性取ε=1. 因此修正后的ILBF总能量泛函为：

(14)

2.2能量泛函的求解

采用变分法，最小化能量泛函F，得到梯度下降流，即水平集函数迭代演化方程：

(15)

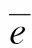
(16)

式中，ci,i=1, 2, 是一种全局信息，由公式(2)给出；fi,i=1, 2, 是一种局部信息，由公式(4)给出. 再用有限差分方法将其数值化，便于计算机进行迭代求解. 当水平集函数演化结束后，取其零水平集即为最终的演化曲线C，图像分割完毕.

3实验结果

实验验证新模型的4个特点: ① 能分割灰度不均的图像； ② 具有一定的抗噪性； ③ 对初始曲线的大小和位置不敏感； ④ 演化速度快，迭代次数少. 程序用MatlabR2010b编写. 数值实现采用简单的中心差分法，时间步长t=0.1，模型参数σ=3，μ=1，λ1=λ2=1，v取值根据不同的图像进行调整，一般由图像的边界大小决定，取值范围在0.001×2552～0.01×2552之间.

在新提出的模型中，w是用来控制局部信息与全局信息拟合能量权值的. 对于灰度严重不均的图像(如图1 (a))，分割的准确性依赖于局部信息，因此，应该选择一个较大的w作为局部信息的权值. 而对于一般的灰度不均匀图像(如图1 (b))，全局信息可以使轮廓线迅速收缩到物体的边缘处，在这种情况下，应该选择略小的w作为局部信息的权值. 在实验过程中，若前景与背景的灰度明显不均，则w取值0.95； 若前景与背景的灰度不均现象不明显，则w可取值0.9.

图1在三幅人工合成和四幅医疗图像中进行，图中绿色线为初始轮廓，红色线为最终的分割结果. 图像大小分别为： 127×96、 127×121、 157×151、 107×180、 406×336、 256×226、 194×255，正确分割出目标边界所需的迭代次数分别为15、 50、 50、 80、 50、 50和30，由图1可知： 新模型在非同质的图像分割中可以取得良好的效果.

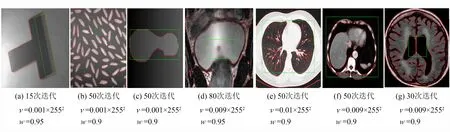
图1　新模型对灰度不均图像的分割Fig.1　Segmentation for the inhomogeneity image

图2比较了LBF模型和ILBF模型的抗噪性. 图像大小为50×50、 80×80、 85×85和 90×70，本文模型的参数v都取值为0.009×2552. 图中绿色线为初始轮廓，红色线为最终的分割结果，第一行为ILBF模型的分割结果，第二行是LBF模型经过200次迭代的分割结果. 由此可知： LBF模型不能分割出目标，陷入局部极小值，将噪点都分割出来，造成误分割，而新模型却能较好地分割出目标. 通过跟LBF模型相比，可知新的模型具有较好的抗噪性.

图2　LBF模型和ILBF模型抗噪性的对比Fig.2　Comparison of LBF and ILBF model’ anti-noise property

图3表明了ILBF模型减轻了对初始轮廓线大小及其位置的敏感性. 图中绿色线为初始轮廓，红色线为最终的分割结果，血管图像大小为103×131，控制参数w取值为0.95，长度项的参数v都取值为0.001×2552. 由图3可以看出： ① 选取一系列相同大小但位置不同的初始轮廓线(如第一行的绿色线所示)时，新模型都只经过20次迭代就得到正确的分割结果(如第一行的红色线所示)； ② 选取一系列相同位置但大小不一的初始轮廓线(如第二行的绿色线所示)时，新模型也只要经过20～100次迭代就得到正确的分割结果(如第二行的红色线所示). 因此，ILBF模型可以有效的对抗初始轮廓线大小及其位置的敏感性.

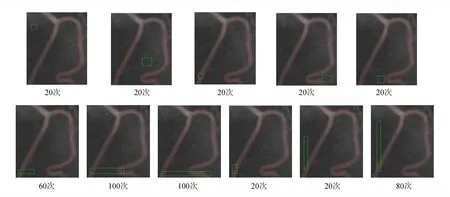
图3　模型对初始轮廓线大小及位置的敏感性Fig.3　Sensitivity for the size and placement of initialization of the curve

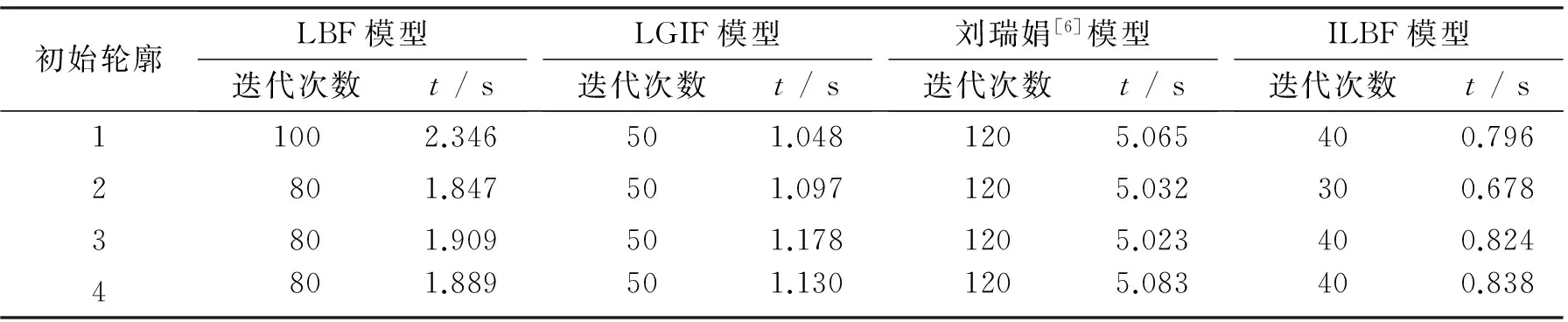
图4中绿色线为4种不同的初始轮廓线，红色线为最终的分割结果，第1、 2、 3、 4列分别为LBF、 LGIF、 刘瑞娟[6]、 ILBF模型的分割结果. 表1列出了图4在实验中4种不同的初始轮廓下各个模型分割出目标边界的迭代次数和时间，表2给出了各个模型的参数值. 由表1可知在分割血管图时，与其它模型相比，新模型能够以更少的迭代次数和CPU时间正确分割出血管.

图4　ILBF模型和LBF、 LGIF、 刘瑞娟[6]模型的对比Fig.4 Comparison of ILBF model with LBF, LGIF and Liu Ruijuan[6] model

初始轮廓LBF模型迭代次数t/sLGIF模型迭代次数t/s刘瑞娟[6]模型迭代次数t/sILBF模型迭代次数t/s11002.346501.0481205.065400.7962801.847501.0971205.032300.6783801.909501.1781205.023400.8244801.889501.1301205.083400.838

表2　图4实验中各个模型参数的取值

4结论

由于LBF模型只在局部拟合项的作用下进行曲线的演化，极易陷入局部极小，导致噪声和初始轮廓的敏感性. 针对该缺点，通过控制参数的调节，融入了全局灰度信息，提出一种融合全局图像信息的局部二元拟合的活动轮廓模型，该模型可以选择有灵活的初始化水平集的函数方式，无需重新初始化，而且该模型集成了LBF模型和 CV模型的优点，具有局部和全局的分割特性，能够广泛地分割灰度不均图像，并具有良好的抗噪性以及减轻了对轮廓线初始化的敏感性，同时通过与文献[4, 6, 9]所提的模型相对比可知，该模型在分割速度、 迭代次数方面得到了改善.

参考文献：

[1] 方江雄. 基于变分水平集的图像分割方法研究[D]. 上海: 上海交通大学, 2012.

[2] 王艳. 图像分割的偏微分方程方法研究[D]. 重庆: 重庆大学, 2012.

[3] CHAN T, VESE L. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277.

[4] LI C, KAO C, GORE J,etal. Implicit active contours driven by local binary fitting energy[C]//Conference on Computer Vision and Pattern Recognition (CVPR). Minneapolis: IEEE Computer Society Press, 2007: 1-7.

[5] 戚世乐, 王美清. 结合全局和局部信息的“两阶段”的活动轮廓模型[J]. 中国图象图形学报, 2014, 19(3): 421-427．

[6] 刘瑞娟, 何传江, 原野. 融合局部和全局图像信息的活动轮廓模型[J]. 计算机辅助设计与图形学学报, 2012, 24(3): 364-371.

[7] 张开华, 周文罡, 张振. 一种改进的C-V主动轮廓模型[J]. 光电工程, 2008, 35(12): 112-116.

[8] ZHANG K, SONG H, ZHANG L. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 43(4): 1 199-1 206.

[9] WANG L, LI C, SUN Q. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation[J]. Computerized Medical Imaging and Graphics, 2009, 33(7): 520-531.

[10] HE C, WANG Y, CHEN Q. Active contours driven by weighted region-scalable fitting energy based on local entropy[J]. Signal Processing , 2012, 92(2): 587-600.

[11] LI C, XU C, GUI C. Level set evolution without re-initialization: a new variational formulation[C]//Conference on Computer Vision and Pattern Recognition(CVPR). San Diego: IEEE Computer Society Press, 2005: 430-436.

[12] LI C, XU C, GUI C. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3 243-3 254.

[13] ZHANG K, ZHANG L, SONG H. Reinitialization-free level set evolution via reaction diffusion[J]. IEEE Transactions on Image Processing, 2013, 22(1): 258-271.

[14] DONG F, CHEN Z, WANG J. A new level set method for inhomogeneous image segmentation[J].Image and Vision Computing, 2013, 31(10): 809-822.

(责任编辑： 洪江星)

A local fitting active contour model involving global information

WU Yiping, SHEN Ming

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

Abstract:We propose a new image segmentation model which is combing local with global intensity of the image. It is a region-based active contour model which improves the local fitting item. With the help of controlling parameter, it can release the work of the local fitting item in local binary fitting (LBF) active contour model and enhance the weight value of the global item. The model can not only deal with the intensity inhomogeneity image segmentation problem, but also be flexible to the initialization of the contour. Experimental results show that the model has released the sensitivity of the placement and size of the contour, improved evolution speed, and decreased CPU time for synthetic and real images.

Keywords:image segmentation; active contour; local fitting; partial differential equation; inhomogeneity intensity

DOI:10.7631/issn.1000-2243.2016.03.0394

文章编号：1000-2243(2016)03-0394-07

收稿日期:2014-03-07

通讯作者:沈明(1983-)，副教授，主要从事非线性偏微分方程及其应用等研究，shenming0516@fzu.edu.cn

基金项目:福建省教育厅科技资助项目(JB12256)

中图分类号：TP391

文献标识码：A