非等间距GM(1,1)模型背景值的改进及其应用
2016-06-23江艺羡张岐山
江艺羡, 张岐山
(福州大学经济与管理学院,福建 福州 350116)
非等间距GM(1,1)模型背景值的改进及其应用
江艺羡, 张岐山
(福州大学经济与管理学院,福建 福州350116)
摘要:根据模型的指数特性以及积分特点,以数据曲线在每个区间[ki-1,ki]与坐标轴所围成的梯形面积作为模型背景值z(1)(ki)与z(1)(ki-1)的差值,并对其进行修正,从而达到对传统非等间距GM(1,1)模型进行优化的目的. 最后采用实例进行验证,并将结果同其他文献的拟合精度进行对比,从而验证算法的有效性与可行性.
关键词:非等间距; GM(1,1)模型; 背景值; 参数优化
0引言
1982年,邓聚龙[1]创立灰色系统理论,它是一种研究少数据、 贫信息的不确定性问题的新方法. 经过几十年的发展,已经在工农业、 社会经济、 能源、 交通等众多领域得到广泛应用[1]. 然而,传统的灰色GM(1,1)模型仅适用于等间距序列的建模与预测. 在实际应用中,却一般存在大量非等间距序列,因此对于非等间距序列的数据拟合或预测,建立非等间距GM(1,1)模型具有重要的现实意义.
针对非等间距GM(1,1)模型存在的问题,已有很多学者对其进行了研究与改进. 谭冠军[2]通过考虑序列的间距重构背景值. 王丰效[3]提出了一类非等间距灰色组合预测方法. 李翠凤等[4]提出了用x(1)(t)在区间[ki,ki+1]上的中点实际值作为背景值. 王叶梅等[5]用非齐次指数函数拟合一次累加生成序列,提出一种重构背景值的方法. 文献[6]采用欧拉公式直接计算非等间距GM(1,1)模型的参数a,b. 文献[7]重新构造背景值公式,并采用二分法求解模型参数. 文献[8]在GM(1,1)建模思想的基础上提出了一种基于直接建模的逐步优化的新息非等间距GM(1,1)模型. 刘萍等[9]提出用加权差值背景值优化非等间距GM(1,1,)模型. 雍华等[10]提出了一种基于求导定义能同时优化非等间距GM(1,1)模型最原始形式的灰导数和背景值的方法. 文献[11]采用非齐次指数离散函数拟合累加序列,重新定义模型背景值. 文献[12]提出一种基于非等时距加权灰色模型和神经网络的组合预测算法.
借鉴已有的文献结果,本研究根据非等间距GM(1,1)模型的指数特性以及积分特点,给出一种利用改进的梯形面积构造方法,从而给出新的背景值公式,优化非等间距模型,对进一步促进非等间距GM(1,1)模型的发展起到一定的推动作用.
1非等间距GM(1,1)模型背景值的优化
定义1[1]设X(0)=(x(0)(k1),x(0)(k2),…,x(0)(kn))为非负序列,若间距Δki=ki-ki-1≠const,则称X(0)为非等间距序列.
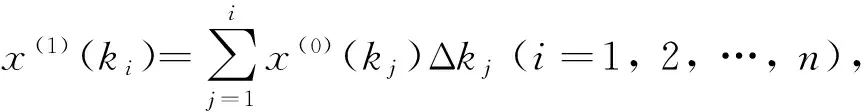

(1)
根据公式(1)可求得如下等式:
(2)
从以上等式分析,相邻背景值的差值z(1)(ki)-z(1)(ki-1)近似等于原数据列曲线在[ki-1,ki]与坐标轴所围成的面积.




根据以上分析,本文拟采用各个区间中梯形的面积作为相邻背景值在该区间的差值,并采用修正算子λ弥补梯形面积与实际面积所造成的差异,即
z(1)(ki)-z(1)(ki-1)
(3)
(4)
因此,本文以公式(4)作为白化方程x(0)(ki)+az(1)(ki)=b的新背景值,后面将采用实例进行验证.
(5)

(6)
(7)
(8)
(9)

(10)
其时间响应序列为:
(11)
(12)
2GM(1,1)模型的建模步骤
综上所述,以定理1优化的非等间距GM(1,1)模型的建模步骤如下.
1) 判断原始数据X(0)是否为准光滑序列(方法参考文献[1]).
2) 若X(0)为准光滑序列,对原始数据做一次累加生成,得到一阶累加生成序列X(1); 若X(0)非准光滑序列,对原始数据进行变换处理,返回步骤1).

3实例分析
针对不同的数据列,利用MATLAB7.0软件,分别应用相关的计算公式,建模计算模型的模拟数据,并利用非等间距GM(1,1)模型的精度检验方法对数据模拟精度进行比较. 本研究选用残差检验法与后验差检验法. 下面以分析钛合金疲劳强度随温度变化为例,详见表1.

表1 钛合金疲劳强度随温度变化关系
计算本文模型对应的模拟数据,并对模型进行精度分析,计算模拟数据与原始数据的残差与相对误差. 数据拟合结果见表2以及图4. 当温度为240 ℃时,模拟值与原始值的残差为5.320 6,相对误差较大,达到1.052 3%.除改点外,其余的残差均小于0.35,相对误差均在理想范围内.数据拟合的整体相对误差为0.176 7%. 模型精度等级为一级. 从图4可以看出除第五个数据模拟值与原始数据有偏移外,其余各点与原始数据几乎重叠,整体而言拟合效果很好.
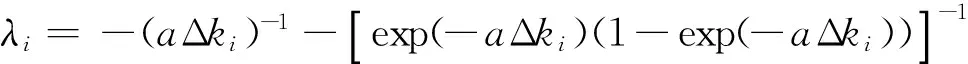

表2 采用本文模型的拟合结果
5结论
传统非等间距GM(1,1)模型一般假定原始数据具有近似指数规律,而传统的利用梯形公式构造背景值的方法使得模型的预测精度与实际稍有偏差. 本研究分析背景值的构造方法,根据黎曼积分的核心思想,以数据曲线在每个区间[ki-1,ki]与坐标轴所围成的梯形面积作为模型背景值z(1)(ki)与z(1)(ki-1)的差值,对传统背景值进行改进,构造新的背景值,从而提高模型精度. 通过对实验数据进行建模,求得优化模型的拟合精度,实验结果验证了本文优化模型的可行性与有效性.
参考文献:
[1] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M]. 北京: 科学出版社,2010.
[2] 谭冠军. GM(1,1)模型的背景值构造方法和应用(Ⅱ)[J]. 系统工程理论与实践,2000,20(5): 125-127.
[3] 王丰效.非等间距组合灰色预测模型[J]. 数学的实践与认识,2007,11,37(21): 39-43.
[4] 李翠凤,戴文战.非等间距GM(1,1)背景值构造方法及应用[J]. 清华大学学报(自然科学版),2007,47(增刊2): 1 729-1 732.
[5] 王叶梅,党耀国,王正新.非等间距GM(1,1)模型背景值的优化[J]. 中国管理科学,2008,16(4): 159-162.
[6] WANG Q F. Parameter estimation of non-equidistant GM(1,1) model based on the euler formula[C]// Proceedings of 2009 IEEE International Conference on Grey Systems and Intelligent Services. Nanjing: IEEE,2009: 378-382.
[7] ZHANG Y,FENG C H. Research on the Background Value of Non-equidistance GM(1,1) Model[C]//Proceedings of 2010 International Conference on Computer Application and System Modeling. Taiyuan: IEEE,2010: 60-62.
[8] 罗佑新.非等间距新息GM(1,1)的逐步优化模型及其应用[J]. 系统工程理论与实践,2010,30(12): 2 254-2 258.
[9] LIU P,WEI Y. A new optimum method of non-equidistance GM(1,1) models’ background value[C]// Proceedings of the 2011 2nd International Conference on Management Science and Engineering Advances in Artificial Intelligence. New jersey: Elsevier B V Press,2011: 330-335.
[10] 雍华,魏勇,孔新海. 同时优化背景值和灰导数的新非等间距GM(1,1)模型[J]. 数学的实践与认识,2011,41(20): 172-178.
[11] ZOU R B. Non-equidistant new information optimum GM(1,1) model and its application[J]. Journal of Mathematical and Computational Science,2012,2(6): 1 909-1 917.
[12] 韩晋,杨岳,陈峰,等.基于非等时距加权灰色模型与神经网络的组合预测算法[J]. 应用数学和力学,2013,34(4): 408-419.
(责任编辑: 林晓)
Improvement of background value in non-equidistant GM(1,1) model
JIANG Yixian, ZHANG Qishan
(School of Economics and Management,Fuzhou University,Fuzhou,Fujian 350116,China)
Abstract:According to the exponential properties and intergral characteristics of model,used the trapezoidal area surrounded by the interval [ki-1,ki] and the axis as the difference of background value z(1)(ki) and z(1)(ki-1),then revised it. Thus achieved the goal to optimize the traditional non-equidistant GM (1,1) model. We tested the model with real data,and compared the fitting precision with other literatures,the results showed the model’s feasibility and efficiency in this paper.
Keywords:non-equidistant; model GM(1,1); background value; parameters optimization
DOI:10.7631/issn.1000-2243.2016.03.0306
文章编号:1000-2243(2016)03-0306-05
收稿日期:2013-12-17
通讯作者:江艺羡(1983-),博士研究生,主要从事灰色系统、 数据挖掘、 智能分析等方面研究,esian108@gmail.com
基金项目:国家自然科学基金资助项目(70871024)
中图分类号:N941.5
文献标识码:A
