具有捕获项及Holling Ⅲ型功能反应的非自治Lotka-Volterra系统的多个正周期解

高 刚，魏凤英

(福州大学数学与计算机科学学院，福建 福州　350116)

具有捕获项及Holling Ⅲ型功能反应的非自治Lotka-Volterra系统的多个正周期解

高 刚，魏凤英

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：研究一个具有捕获项及Holling III型功能反应的非自治Lotka-Volterra系统，利用重合度理论中的Mawhin连续定理，得到了该系统2n+m个正周期存在的充分条件, 并举例说明所得结论的有效性.

关键词：正周期解； 重合度理论； 捕获； Holling III型功能反应； Lotka-Volterra系统

0引言

近些年，关于生物捕食者-食饵模型多个周期解存在问题被广泛地研究，也取得了一些比较好的成果. 在捕食者-食饵系统多个周期解的研究中, 生态系统通常只含有一个捕食者和一个食饵, 或者系统内部是食物链的情况[1-5]. 然而, 在自然界中都会存在多个捕食者和多个食饵的复杂生态系统. 赵凯宏等[6]研究了一类具有捕获者、 非自治的Lotka-Volterra捕食者-食饵系统：

(1)

文献[7-8]在系统(1)的基础上，考虑脉冲对于生态种群的影响，利用重合度理论中的Mawhin连续定理，得到多个正周期解存在的充分条件. 系统(1)中讨论的是n个食饵种群和m个捕食者种群的捕食关系. 由于实际生态系统中，许多生物种群之间的捕食关系函数和营养转移函数需要考虑捕食者捕食的饱和程度，饱和程度表现为捕食者对食饵的功能性反应函数.主要针对脊椎类动物种群之间的捕食关系，考虑捕食者对食饵的功能性反应函数，并结合以往的研究成果，研究一类具捕获项及Holling III型功能反应非自治的Lotka-Volterra捕食者-食饵系统:

(2)

其中: i=1, 2, …, n; j=1, 2, …, m, 若无特殊说明，所涉及角标均源于此.

系统(2)中含有m个捕食者种群及n个食饵种群，xi(t)和yn+j(t)分别表示食饵种群及捕食者种群在t时刻种群密度； ai(t), bi(t)和hi(t)分别表示第i个食饵种群的内禀增长率、 种内竞争率和捕获率； αj(t), βj(t)和ej(t)分别表示第j个捕食者种群的内禀增长率、 种间竞争率和捕获率； cil(t)(i≠l)表示第i个食饵种群和第l个食饵种群之间的竞争率； γjl(t)(j≠l)表示第j个捕食者种群和第l个捕食者种群之间的竞争率； dik(t)表示第k个捕食者种群对第i个食饵种群的捕食率； δjk(t)表示第j个食饵种群转化为第k个捕食者种群的转化率； 且ai(t), bi(t), αj(t), βj(t), cil(t), γjl(t), dik(t), δjk(t), hi(t), ej(t), fik(t), gjk(t)在R+=[0, ∞)上都是连续有界正值周期函数.

12n+m个周期解的存在性

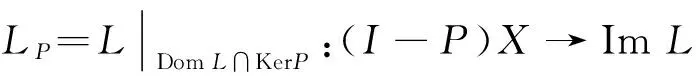
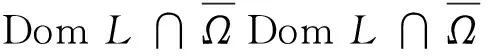
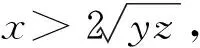
定理1若条件(H1), (H2)成立, 则系统(2)至少存在2n+m个正ω-周期解.

证明对系统(2)作变换xi(t)=exp(ui(t)), yn+j(t)=exp(un+j(t))得到

(3)

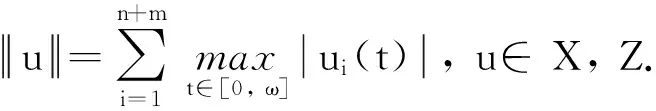
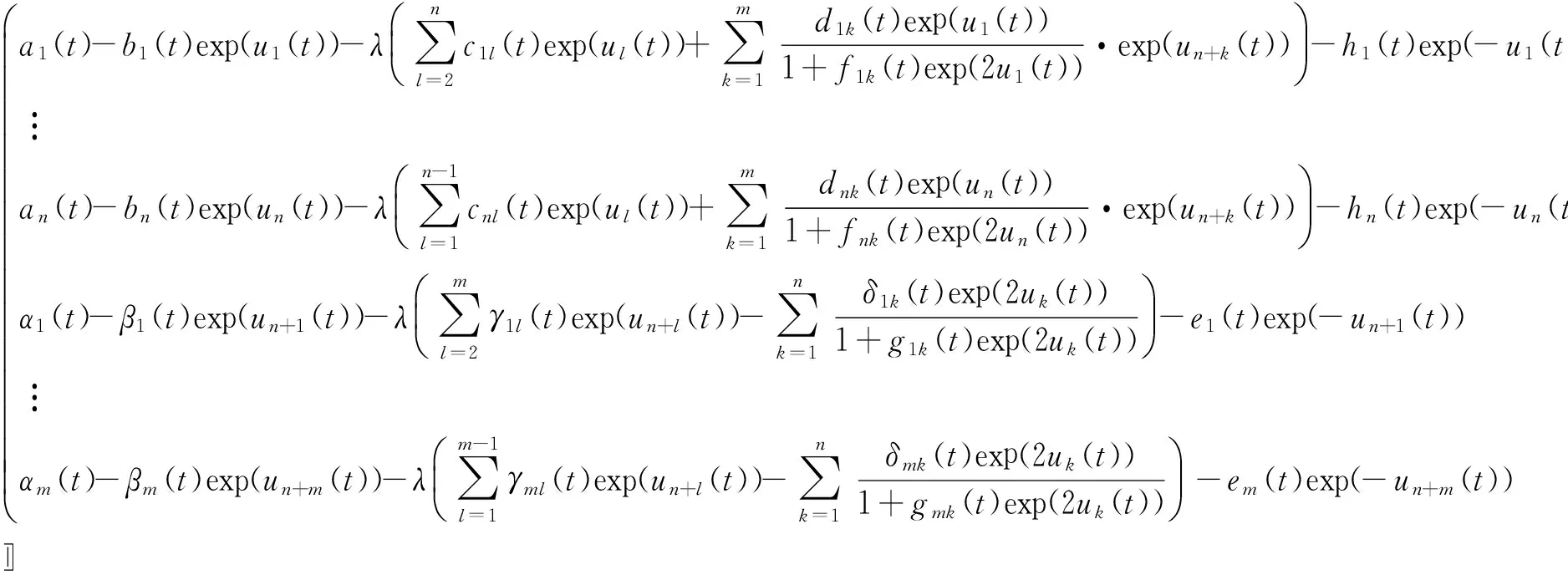
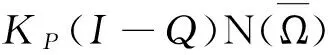
(4)

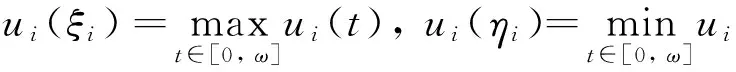
(5)

(6)

(7)

(8)

则由式(5)，有

(9)

(10)

(11)

由(7)～(10)式，得到

(12)

从(9)～(12)式和引理2，对于任意t∈R+有

(13)

ΩK={u=(u1, u2, …, un+m)T∈C(R+, Rn+m)∈X:ui(t)∈Δi, t∈R+, i=1, 2, …, n+m}

易知ΩK是X中的有界开子集，Ωi∩Ωj=∅, i≠j. 则引理1的1)成立.

反证法，若u∈∂Ωk∩KerL=∂Ωk∩Rn+m，QN(u, 0)=(0, …, 0)T，k=1, 2, …, 2n+m，则

根据积分的性质知，存在ti∈R+, i=1, 2, …, n，tn+j∈R+, j=1, 2, …, m，使

(14)

由(14)式，可得

ai(ti)-bi(ti)exp(xi)-hi(ti)exp(-xi)=0，αj(tn+j)-βj(tn+j)exp(yn+j)-ej(tn+j)exp(-yn+j)=0

(15)

(16)

综上，引理1的1)～3)都成立. 因此系统(4)至少有2n+m个不同的ω-周期解，从而系统(2)至少有2n+m个不同的ω-周期解. 证毕.

2例子

考虑具有捕获项及Holling III型功能性反应的一食饵两捕食者系统：

(17)

参考文献：

[1] HU D W，ZHANG Z Q. Four positive solutions to a Lotka-Volterra cooperative system with harvesting terms[J]. Nonlinear Analysis： Real World Applications，2010，11(2)： 1 115-1 121.

[2] ZHAO K H，YE Y. Four positive periodic solutions to a periodic Lotka-Volterra predatory-prey system with harvesting terms [J]. Nonlinear Analysis: Real World Applications，2010，11(4)： 2 448-2 455.

[3] WEI F Y. Existence of multiple positive periodic solutions to a periodic predator-prey system with harvesting terms and Holling-III type functional response[J]. Communications in Nonlinear Science and Numerical Simulation，2011，16(4)： 2 130-2 138.

[4] 谢燕霞，魏凤英. 一类具有阶段结构和Holling-II类功能性反应的多种群捕食系统[J]. 福州大学学报(自然科学版)，2010，38(1)： 1-5.

[5] 雷慧榕，魏凤英. 具有捕获的四种群捕食系统的多个正周期解[J]. 福州大学学报(自然科学版)，2011，39(2)： 167-173.

[6] ZHAO K H，LI Y K. Multiple positive periodic solutions to a non-autonomous Lotka-Volterra predator-prey system with harvesting terms[J]. Electronic Journal of Differential Equations，2011(49)： 1-11.

[7] LI Y K，YE Y. Multiple positive almost periodic solutions to an impulsive non-autonomous Lotka-Volterra predator-prey system with harvesting terms[J]. Communications in Nonlinear Science and Numerical Simulation，2013，18(11)： 3 190-3 201.

[8] FAN X M，JIANG F Q，ZHANG H N. Dynamics of multi-species competition-predator system with impulsive perturbations and Holling type III functional responses[J]. Nonlinear Analysis： Theory，Method & Applications，2011，74(10)： 3 363-3 378.

[9] 郭大钧，孙经先，刘兆理. 非线性常微分方程泛函方法[M]. 济南： 山东科学技术出版社，2006.

(责任编辑： 林晓)

Multiple positive periodic solutions of a nonautonomous Lotka-Volterra system with harvesting terms and Holling III functional response

GAO Gang, WEI Fengying

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou，Fujian 350116, China)

Abstract:We consider a nonautonomous Lotka-Volterra system with harvesting terms and Holling type III functional response in this contribution. By using of Mawhin’s continuation theorem of coincidence degree theory, we establish the existence of 2n+mpositive periodic solutions for the system. An example is given to illustrate the effectiveness of our results.

Keywords:positive periodic solutions； coincidence degree； harvesting terms； Holling III functional response； Lotka-Volterra system

DOI:10.7631/issn.1000-2243.2016.03.0315

文章编号：1000-2243(2016)03-0315-05

收稿日期:2013-09-30

通讯作者:魏凤英(1976- )，教授，主要从事随机微分方程与生物数学研究，weifengying@fzu.edu.cn

基金项目：国家自然科学基金资助项目(11201075)； 福建省自然科学基金资助项目(2016J01015)

中图分类号：O175

文献标识码：A