大型复杂结构安定性数值分析的新方法及其应用
2016-06-23邹宗园郭宝峰毛春燕
邹宗园 郭宝峰 金 淼 毛春燕
1.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,0660042.太原重工股份有限公司,太原,030024
大型复杂结构安定性数值分析的新方法及其应用
邹宗园1郭宝峰1金淼1毛春燕2
1.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,0660042.太原重工股份有限公司,太原,030024
摘要:大型复杂结构承载后普遍存在局部高应力区,特别是某些巨型结构,由于受几何尺寸和制造能力的限制,其局部高应力往往会接近甚至超过材料的屈服极限,因而成为弹性范围内的设计难题。应用安定性分析设计准则,则可通过利用材料的塑性承载能力很好地解决这类问题。为此,在大型复杂结构的强度分析中引入安定性理论,应用Melan安定下限定理,通过将峰值载荷下的弹塑性应力场与弹性参考应力场相减,构造定理要求的自平衡应力场,并推导了相应的安定性判定条件。在此基础上,结合弹塑性增量有限元技术,通过不同载荷水平下的加载-卸载计算,计算相应载荷水平下的残余应力场。根据加载-卸载得到的残余应力场与构造的自平衡场的关系,按照安定性判定条件确定安定极限载荷,从而建立了一种适合于大型复杂结构安定性数值分析的新方法,并应用该方法对某125 MN锻造液压机的主液压缸缸体结构进行了安定性分析。
关键词:弹塑性;安定性;液压缸;安定极限载荷;局部高应力
0引言
在工业制造领域,一些大型复杂承载结构,因其构件尺寸大、结构复杂,承载后应力分布不均匀,即使经过结构优化设计也不可避免地在结构局部形状和尺寸发生突变的位置产生应力集中,形成高应力区。这些局部高应力往往是结构中平均应力的2~5倍,常常接近甚至超过材料的屈服极限。例如,大型液压机本体结构中的法兰支撑式液压缸,其法兰根部圆角区域局部受力状态复杂,且存在应力集中而出现局部高应力,所以其法兰与缸筒的过渡部位一直是这种结构强度分析校核的关键控制部位,即使采用了经过优化设计的过渡型线也无法避免局部高应力现象的发生。
根据安定理论,对于弹性安定的结构,在初始承载循环后会产生局部塑性变形,但在结构安定之后便不再有新的塑性变形产生,结构表现为完全弹性响应。也就是说,即使在局部高应力区产生了塑性变形,结构也可能进入安定状态,并不会发生弹塑性强度破坏。安定理论合理地利用了材料的塑性承载能力,无需再将结构的最大应力控制在材料许用应力之内。
显然,若引入安定性理念,以结构的安定极限载荷作为结构的弹塑性承载能力界限,那么对于存在局部高应力区的大型复杂承载结构而言,就意味着能够更充分地利用材料的弹塑性承载能力。现阶段,基于安定理论的弹塑性强度设计准则已经被写入ASME Ⅷ-2[1]和EN-13445[2]等压力容器建造规范。除了在压力容器[3-4]的设计校核中得到应用外,也在核电工业构件[5-6]、航空航天构件[7]、铁路道轨[8]、土工地基[9]、近海结构[10]及钢结构框架[11]的分析设计中得到了应用。为促进安定理论的应用,已发展了许多安定性数值分析方法。这些方法包括直接循环法和基于安定定理的数值计算方法,如数学规划法、弹性补偿法等。然而直接循环法需进行不同载荷下的多次循环计算,繁琐耗时[12];其他数值计算方法则需通过编制子程序,嵌入商业有限元软件中实现分析[13-15],各有优势但又存在其应用的局限性,尚无法简便有效地实现液压机本体结构的安定性分析。
本文针对存在局部高应力的大型复杂承载结构的强度分析问题,引入安定理论并根据Melan安定下限定理建立了一种应用弹塑性增量有限元技术求解结构安定极限载荷的数值分析新方法,并应用该方法对125 MN锻造液压机主缸进行了安定性分析。
1安定性数值分析方法
1.1安定性判定条件
Melan安定定理描述为,对于理想弹塑性结构,如果存在一个时间无关的自平衡应力场,使得结构内的任何点在加载域内的所有载荷下,其与假设结构为理想弹性体时的弹性参考应力场叠加后得到的应力场满足如下条件则结构安定:
(1)
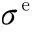
根据上述定理,可以通过构造时间无关的自平衡应力场来求解满足安定下限定理的最大外载荷,即安定极限载荷。
液压机本体结构件受到工作载荷的循环加载-卸载作用。液压缸的循环工作载荷可表示为
P(t)=P(t+T)
(2)
式中,T为载荷循环周期;P(t)∈[0,P]为载荷域。
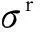
(3)
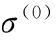
由于载荷域P(t)∈[0,P]为一维加载域,且弹性参考应力是与载荷成正比的,所以在整个载荷域内的安定性可以通过载荷域两个顶点处即谷值、峰值处进行判断即可。因此若要满足安定下限定理的安定条件(式(1)),则在循环载荷谷值、峰值处均需满足式(1),即
(4)
(5)
将式(3)代入式(5)可得
(6)
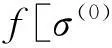
1.2数值方法的实现
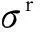

图1 安定性数值分析方法的加载路径
对于图1所示的峰值渐增的加载路径,第一个载荷峰值一般可选为结构的设计载荷,载荷峰值的增幅ΔP则可根据计算精度要求进行确定。

图2 安定极限载荷的确定
由于结构的安定性取决于其强度最薄弱部位的关键点,所以安定性数值分析只需监测其关键点。那么,对于理想弹塑性材料结构,关键点的等效残余应力σr首次等于材料的屈服极限σs时所对应的载荷Ps为安定极限载荷,如图2所示。因此,通过从有限元分析结果中提取结构关键点在不同载荷峰值下加载-卸载结束时应力状态的等效应力就可方便地确定结构的安定极限载荷。图3所示为上述安定性数值分析流程。
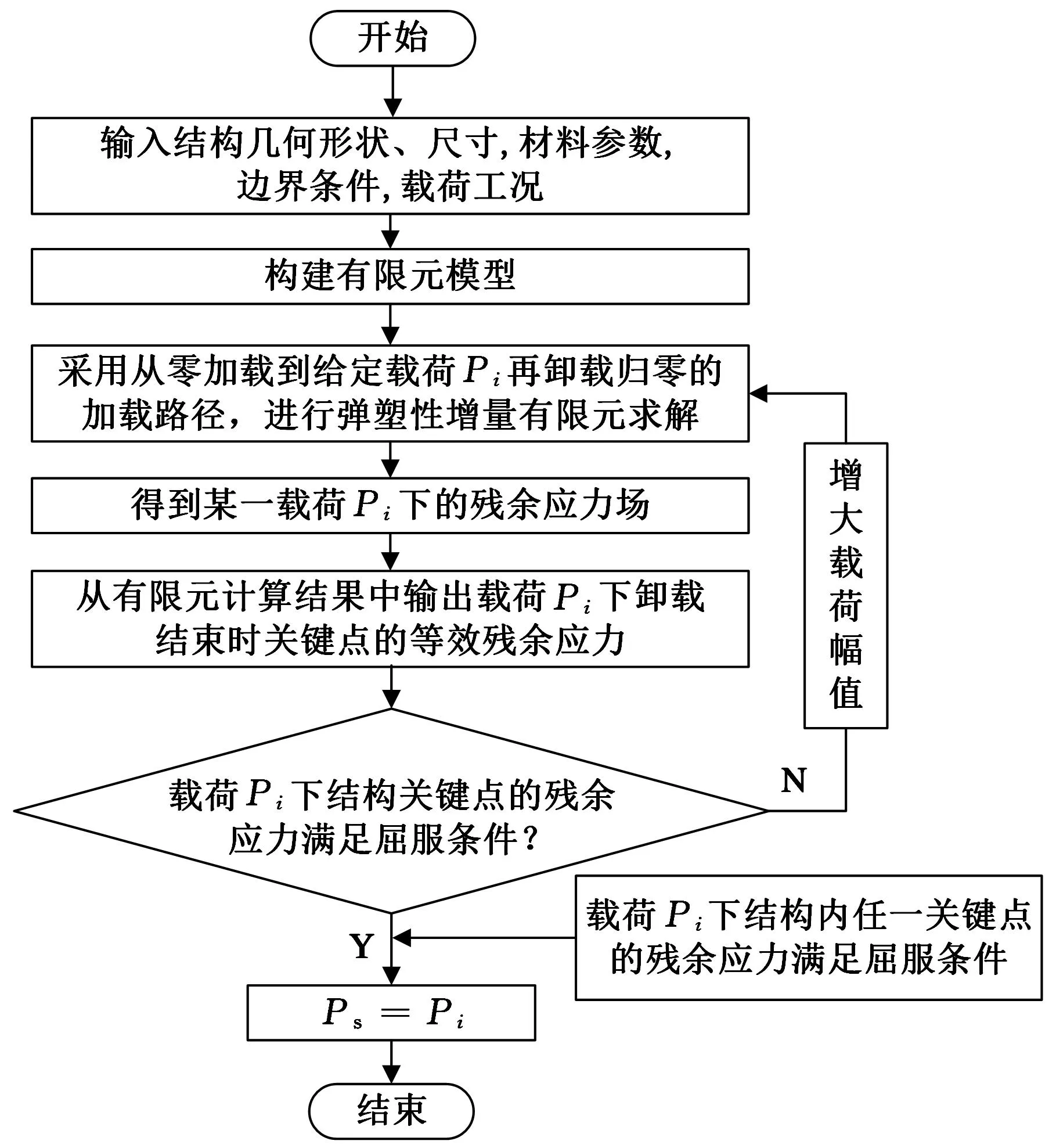
图3 安定性有限元数值分析流程图
2液压缸安定性分析
2.1有限元模型
图4是某125 MN自由锻造液压机主液压缸的缸体结构简图。该液压缸为法兰支撑结构,支撑法兰位于缸口。缸体按照弹性范围的强度设计准则设计完成。液压缸的额定工作压力为35 MPa。缸体材质为锻钢35,其屈服极限不小于235 MPa。缸体的有限元弹性强度分析结果表明,在缸筒与法兰的圆角过渡区域存在局部高应力,最高应力值已接近材料的屈服极限,那么,根据弹性强度设计准则,其安全系数(材料屈服极限与最高应力的比值)略大于1,因此缸体的弹性强度安全裕度非常有限。但在液压机投产以来3年多的运行实践中,并未出现因液压缸缸体强度不足而导致的异常情况。有鉴于此,应用上述安定性数值分析方法对该液压缸缸体进行了弹塑性强度分析。
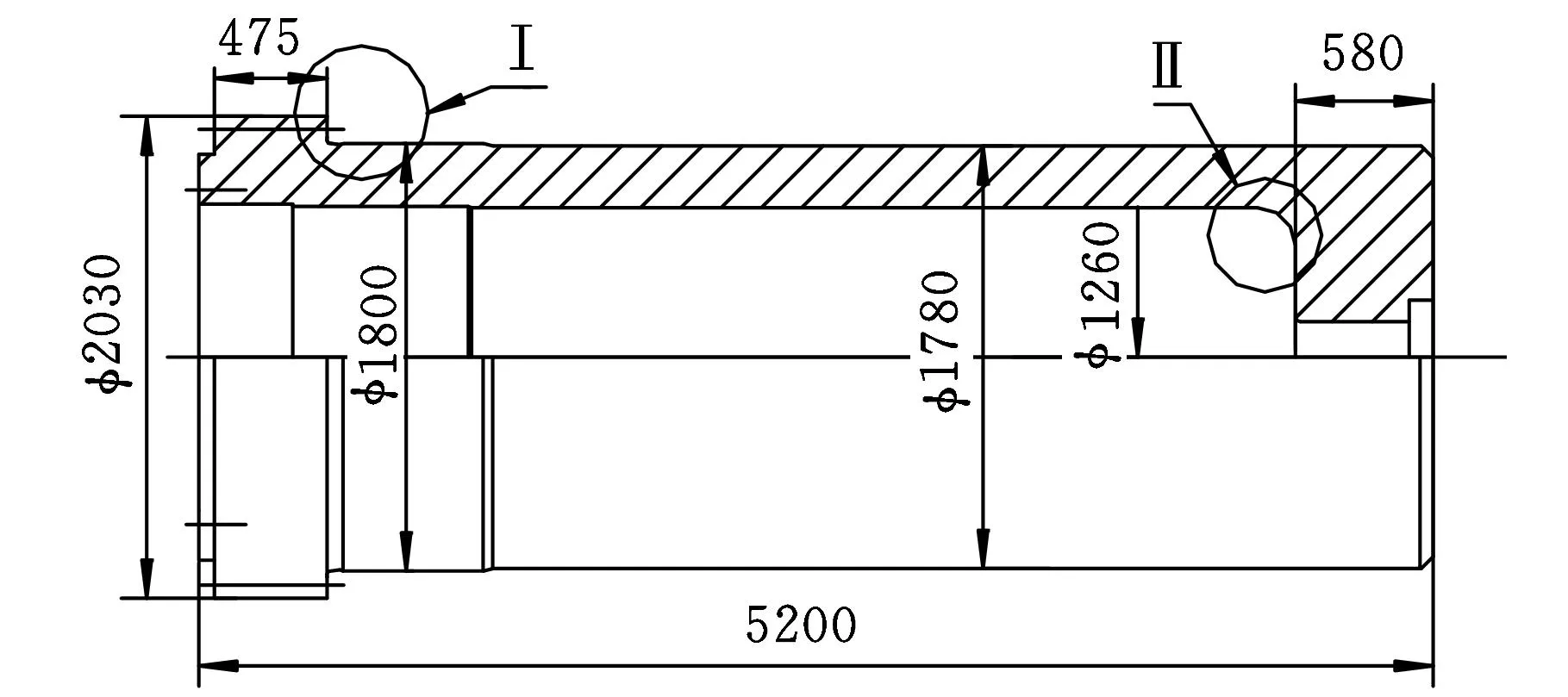
(a)缸体简图

(b)局部放大图Ⅰ(c)局部放大图Ⅱ图4 液压缸缸体结构简图
由于螺栓孔及横梁的弯曲变形对缸体高应力区影响很小,所以在建立缸体有限元模型时进行了简化处理。但在上横梁与法兰及缸筒接触的位置处,上梁的局部挤压变形会对法兰和缸筒相应位置的高应力区的受力状态有较大影响,因此在建立有限元模型时需考虑上横梁下面板局部变形的影响。上横梁材质为ZG270-500,屈服极限取为270 MPa,其下面板局部实体模型的形状和尺寸见图4b,设置它与缸体的接触计算条件,摩擦因数取为0.12。为简单起见,假设缸体和上横梁材料均为理想弹塑性材料,服从Mises屈服准则,有限元模型中缸体屈服极限取为235 MPa。
有限元模型采用了平面四边形四节点单元。对法兰圆角、缸底圆角附近区域进行了局部网格细化处理。细化区形状尺寸如图4b和图4c中虚线所示。基于网格敏感性分析结果,细化和非细化区域的网格边长分别取为1 mm和8 mm。缸体共163 785个单元,上横梁共划分了35 165个单元。
在缸体内壁密封以上部分施加均匀分布的液体压力,密封段总高240 mm,在密封高度范围内按照线性分布规律从上到下施加递减的液体压力。在横梁局部实体模型上施加相应的位移约束。缸体轴对称模型的受力简图见图5,缸体的轴对称有限元分析模型如图6所示。

图5 缸体的加载力学示意图

图6 缸体的有限元模型
应用本文提出的安定性分析新方法对该缸体进行分析计算。施加图1所示的峰值逐渐增大的压力载荷,第一个压力载荷的峰值为35 MPa,之后压力载荷的峰值逐渐增大,每次增幅为1 MPa。
2.2计算结果与讨论
图7是压力为35 MPa时缸体的等效应力云图。最高应力出现在法兰圆角附近区域,等效应力高达230 MPa左右。其他区域的等效应力均小于150 MPa。

图7 压力为35 MPa时的缸体等效应力云图
法兰圆角区域为缸体的最高应力区,所以为缸体安定性判定的关键位置。由载荷峰值逐渐增大的加载-卸载计算得到,缸体法兰圆角区域的关键点的最大等效残余应力与压力载荷的关系如图8所示。根据上文的安定载荷判定条件可知,该液压缸缸体的安定极限压力为68 MPa。
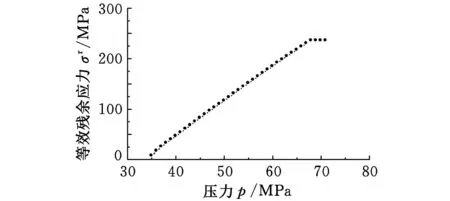
图8 关键点的等效残余应力与压力的关系曲线
压力载荷为68 MPa时缸体的等效应力分布如图9所示。缸体法兰圆角区域的局部应力达到屈服极限,产生局部塑性变形。为了进一步考察液压缸多次循环承载后塑性变形的演化情况,按照从零到68 MPa再到零的载荷循环方式,对缸体进行了50次循环弹塑性增量有限元分析计算。每次加载结束时法兰圆角区域的等效塑性应变率云图见图10。由于等效塑性应变率不为零的区域为塑性变形区,所以由图10可见,在初始循环阶段法兰圆角区域存在局部塑性变形区,随着循环次数的增加,塑性变形区逐渐减小,最后变成完全弹性响应区,达到安定状态。其中塑性应变最大点的总塑性应变随载荷循环数的变化曲线如图11所示。由图11可见,经过初始几个循环后塑性变形稳定不变,不再有新的塑性变形产生,达到安定状态,稳定后的总塑性应变为0.22%。

图9 压力载荷为68 MPa时缸体的等效应力云图
由此可见,由于以安定极限载荷作为缸体的弹塑性强度界限,利用了缸体材料的塑性承载能力,所以缸体即便是在68 MPa的压力下也能够安全服役。
由上述安定性分析结果可知,该液压缸的安定极限压力与额定工作压力的比值约为1.94,说明该缸体的弹塑性强度安全裕度较为宽裕。
3结论
(1)提出了一种安定性数值分析新方法。该方法通过构造合适的自平衡应力场,根据Melan安定下限定理,给出了安定性判定条件,并结合弹塑性有限元技术实现了结构的安定性分析。

(a)第1个循环
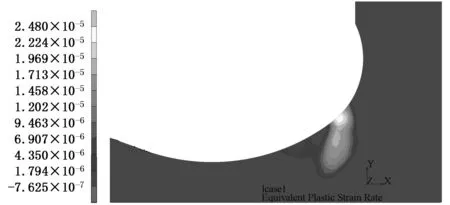
(b)第5个循环
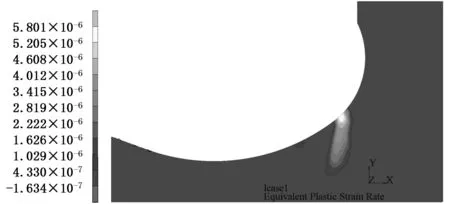
(c)第8个循环
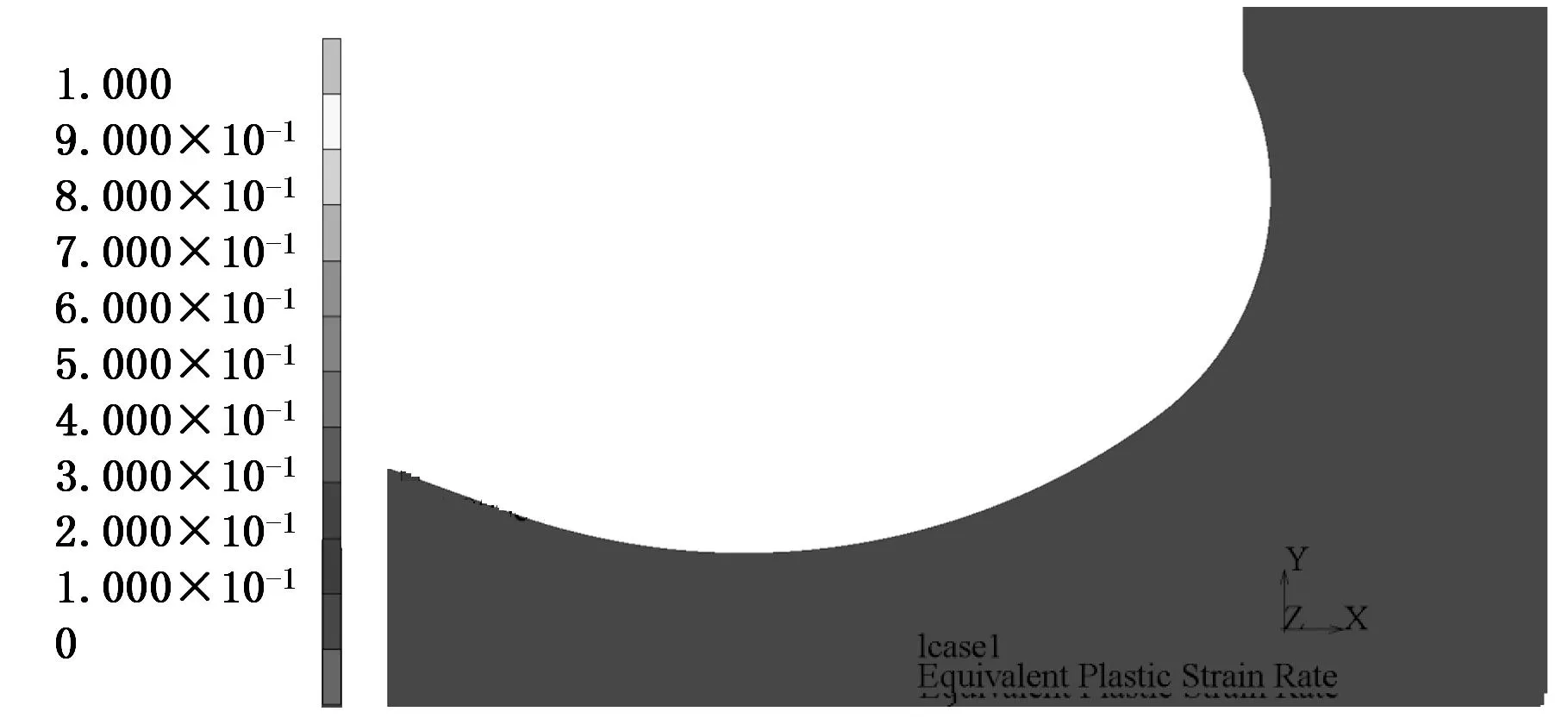
(d)第18个循环图10 不同载荷循环次数下法兰圆角区域的等效塑性应变率云图

图11 关键点的总等效塑性应变随循环数的变化曲线
(2)125 MN自由锻液压机主液压缸缸体的安定性分析结果显示,缸体的弹塑性安全裕度为1.94,可以在高于其额定工作压力90%的情况下正常安全服役。
(3)本文提出的数值方法可以简便有效地实现大型复杂承载结构的安定性分析,可以更合理地解决存在局部高应力区的大型复杂承载结构的强度分析问题。
参考文献:
[1]ASME. ASME-Ⅷ-2 Boiler and Pressure Vessel Code[S]. New York: the American Society of Mechanical Engineers, 2007.
[2]European Commission. EN-13445 Unfired Pressure Vessels[S]. Brussels: European Committee for Standardization, 2002.
[3]Abdalla H F. Shakedown Boundary Determination of a 90 Degrees Back-to-back Pipe Bend Subjected to Steady Internal Pressures and Cyclic In-plane Bending Moments[J]. International Journal of Pressure Vessels and Piping, 2014, 116: 1-9.
[4]Simon J W, Chen Geng, Weichert D. Shakedown Analysis of Nozzles in the Knuckle Region of Torispherical Heads under Multiple Thermo-mechanical Loadings[J]. International Journal of Pressure Vessels and Piping, 2014, 116: 47-55.
[5]Mishra A, Kumar R S, Chellapandi P. Progressive Deformation Behaviour of Thin Cylindrical Shell under Cyclic Temperature Variation Using Combined Hardening Chaboche Model[J]. Latin American Journal of Solids and Structures, 2014, 11(6): 980-992.
[6]Abdalla H F. Elastic Shakedown Boundary Determination of a Cylindrical Vessel-nozzle Intersection Subjected to Steady Internal Pressures and Cyclic Out-of-plane Bending Moments[J]. Nuclear Engineering and Design, 2014, 267: 189-196.
[7]Vermaak N, Valdevit L, Anthony E, et al. Implementations of Shakedown for Design of Actively Cooled Thermo Structural Panels[J]. Journal of Mechanics of Materials and Structures, 2011, 6: 9-10.
[8]Brouzoulis J, Torstensson P T, Stock R, et al. Prediction of Wear and Plastic Flow in Rails—Test Rig Results, Model Calibration and Numerical Prediction[J]. Wear, 2011, 271: 92-99.
[9]Tafreshi S N M, Khalaj O, Dawson A R. Repeated Loading of Soil Containing Granulated Rubber and Multiple Geocell Layers[J]. Geotextiles and Geomembranes, 2014, 42(1): 25-38.
[10]Fadaee M J, Saffari H, Tabatabaei R. Shakedown Limit of Elastic-plastic Offshore Structures under Cyclic Wave Loading[J]. Ocean Engineering, 2008, 35(17/18): 1854-1861.
[11]Atkociunas J, Venskus A. Optimal Shakedown Design of Frames under Stability Conditions According to Standards[J]. Computers & Structures, 2011, 89(3/4): 435-443.
[13]Chen Shenshen, Liu Yinghua, Li Jun, et al. Performance of the MLPG Method for Static Shakedown Analysis for Bounded Kinematic Hardening Structures[J]. European Journal of Mechanics A/Solids, 2011, 30(2): 183-194.
[14]Ure J, Chen Haofeng, Tipping D. Integrated Structural Analysis Tool Using the Linear Matching Method Part 1-Software Development[J]. International Journal of Pressure Vessels and Piping, 2014, 120:141-151.
[15]Simon J W, Hoewer D, Weichert D. A Starting-point Strategy for Interior-point Algorithms for Shakedown Analysis of Engineering Structures[J]. Engineering Optimization, 2014, 46(5): 648-668.
(编辑苏卫国)
A New Shakedown Numerical Analysis Method for Huge Complex Strcuture and Its Applications
Zou Zongyuan1Guo Baofeng1Jin Miao1Mao Chunyan2
1.Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University),Ministry of Education of China,Qinhuangdao,Hebei,066004 2.Taiyuan Heavy Industry Co.,Ltd.,Taiyuan,030024
Abstract:The local high stresses appeared commonly in a loaded huge complex structure. Some of them were usually close to or even exceed the material yield strength due to the restrictions of the geometric size and the practical manufacture. It was troublesome with the applications of the conventional elastic strength design rule. The elastic-plastic shakedown design rule might utilize the plastic bearing capacity of material, then to solve this kind of strength problem well. Thus the shakedown theorem was introduced, and based on Melan shakedown theorem, a self-equilibrium stress field was constructed by subtractting the elastic-plastic stress field and the elastic reference stress field of the peak load, and the corresponding shakedown condition was derived. Then with the applications of the elastic-plastic incremental finite element technique, the loading-unloading calculations for different load levels were conducted to obtain the residual stress fields. Taking consideration of the relation between the residual stress field and the constructed self-equilibrium stress field, the shakedown limit load was determined by the shakedown conditions. Then a shakedown numerical analysis method for huge complex structure was established. The shakedown analysis for the main hydraulic cylinder of a 125 MN forging hydraulic press was performed by this new method.
Key words:elastic-plastic;shakedown;hydraulic cylinder body;shakedown limit load;local high stress
收稿日期:2015-08-17
基金项目:国家科技重大专项(2013ZX04003031);国家自然科学基金资助项目(51475408);河北省高校创新团队领军人才培育计划资助项目 (LJRC012);河北省自然科学基金资助项目(E2015203223)
中图分类号:TG315.4
DOI:10.3969/j.issn.1004-132X.2016.03.013
作者简介:邹宗园,女,1986年生。燕山大学机械工程学院博士研究生。郭宝峰,男,1958年生。燕山大学机械工程学院教授、博士研究生导师。金淼(通信作者),男,1968年生。燕山大学机械工程学院教授、博士研究生导师。毛春燕,女,1978年生。太原重工股份有限公司技术中心工程师。
