数控机床温度敏感点变动性及其影响

苗恩铭　刘　义　高增汉　刘　辉

合肥工业大学，合肥，230009

数控机床温度敏感点变动性及其影响

苗恩铭刘义高增汉刘辉

合肥工业大学，合肥，230009

摘要：数控机床热误差补偿技术中的核心问题是建立能够反映机床温升与热误差之间的数学模型，其精度和稳健性则取决于模型自变量能否准确地反映机床温度场分布特性，即温度敏感点选择结果是否准确和稳定。通过对Leaderway-V450型数控加工中心主轴Z向的多批次空转数据进行分析发现，温度敏感点存在变动性特征，导致自变量间多重共线性程度发生变化，进而对模型的预测精度和稳健性产生严重影响。由于主成分回归算法具有消除自变量共线性影响作用，故提出采用该算法进行建模，并通过实际机床进行实践检验。结果表明，采用主成分回归算法建模，显著降低了温度敏感点变动性对模型预测精度的影响，能保证模型具有很好的预测精度和稳健性。

关键词：数控机床；温度敏感点；多重共线性；主成分回归

0引言

在数控机床加工过程中，机床各部件不均衡温升引起的热误差使得刀具和工件之间的相对正确位置发生了变化，从而造成零件的加工误差。据统计，数控机床热误差约占总误差的50%～70%[1-2]。通过应用设计和制造技术改进床身结构的硬件补偿方法，不仅成本高，而且效果并不十分理想。因此，对数控机床热误差软件补偿技术进行研究具有重要意义[3]。

在数控机床软件热误差补偿技术中，核心问题是建立预测精度高、稳健性强的数学模型[4]。目前国际上通常是在数控机床上布置大量的温度传感器，通过建立传感器温度变量与机床热误差的函数关系来建立数控机床热误差补偿模型[5]。这就要求温度传感器的安放位置既能最大限度地反映温度场的分布特性，又能保证各传感器之间具有较低的共线性干扰以实现模型的稳健性预测，这些位置称之为温度敏感点[6]。近年来，科研人员对温度敏感点的选择进行了大量研究。Attia等[7]采用有限元方法分析机床整体温度场，并将温度场划分为多个比较规则的单元，通过温度场仿真和相关性选择，预测温度测点的最优数量和最佳分布。Lo等[8-9]对温度传感器进行分组搜索、寻优，利用相关性分组、典型变量搜索和分组搜索等方法，达到优化温度测点分布的目的。Lee等[10]采用相关系数和线性回归相结合的方法对温度变量进行优化，以最小残差平方和作为选择温度变量的依据，有效地减少了建模所需的温度测点。杨建国等[11]提出了数控机床热误差分组优化建模方法；苗恩铭等[12-13]利用模糊聚类结合灰色关联度的方法对温度敏感点进行了相关研究。

上述研究中均假设温度敏感点具有稳定性，即对于同一台数控加工中心，根据在此机床上得到的多组实验数据，其温度敏感点计算结果均一致。然而数控机床是一个复杂的装配体结构，实际运作时，温度敏感点能否在环境温度及主轴转速等加工参数变化状态下仍保持稳定，如果温度敏感点发生变动，是否会对模型精度产生影响，这些均未见相关文献报道。

笔者按照ISO 230-3-2001《机床检验通则 第3部分：热效应的确定》的规定，在Leaderway-V450型数控机床主轴空转时进行了多批次实验。采用模糊聚类结合灰色关联度的方法分析各批次数据的温度敏感点，根据各批次数据的敏感点变量建立回归模型，并对模型精度及稳健性进行分析。计算结果证明，不同批次数据的温度敏感点并不完全相同，且根据敏感点变量建立的补偿模型预测稳健性较差。因此，如何在温度敏感点变动的状态下，仍保持模型预测精度的稳健性，是数控机床热误差建模技术中的重要问题。

为解决上述问题，需要从温度敏感点选择与机床热变形模型预测性能的关系上进行分析。温度敏感点变动会实质造成模型自变量间的共线性发生变化，进而对模型的预测精度产生影响，也使得热误差模型的预测稳健性降低。为此，本文提出具有消除共线性影响功能的主成分回归(PCR)建模方法，并结合实际机床热误差空转数据对其进行精度检验，验证了该方法的可行性。

1主成分回归

主成分回归[14]是利用原自变量的主成分代替原自变量作回归分析的一种多元统计方法。由于各主成分间互不相关，且保留了原指标的绝大部分信息，因此利用主成分回归可以有效地解决回归分析中自变量共线性问题。主成分回归方法的具体步骤如下：

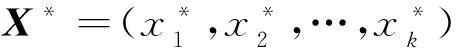
(1)

其中，u1,u2,…,uk为X*的相关系数矩阵的特征向量。

(2)根据累积贡献率选择主成分的个数。第g个主成分的累积贡献率Vccg为

(2)

通常所取的g满足Vccg≥85%。

(3)将标准化的被解释变量关于主成分Z1,Z2…,Zg进行回归，得

(3)

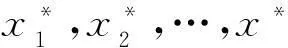
系数βi与原回归模型参数bi间的关系为

(4)

其中,sy、si分别为原始数据y和xi的标准差，由此得原回归模型：

2数控机床热误差实验设计

2.1实验装置

本文以Leaderway-V450型数控加工中心热误差为研究对象。由于该机床的X向和Y向为近似对称结构，相对于Z向，其热变形量较小，并且三轴的数据处理方式相同，故本文仅以该机床的主轴Z向热变形为研究对象，论述温度敏感点变动性对模型影响特征。各传感器的安放位置及作用如表1所示，温度传感器和电感测微仪具体分布位置如图1所示。

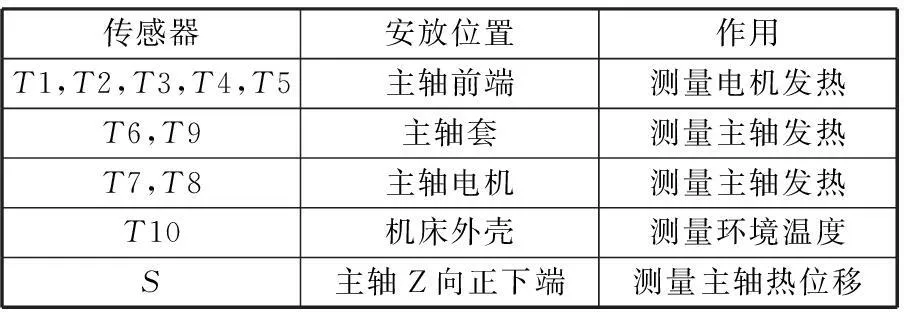
表1　传感器安放位置及作用

图1　温度传感器和电感测微仪的安放位置

2.2实验计划

本文按照ISO230-3-2001规定，实验采用空转方式运行，对不同季节进行了多组数据采样。测量时，温度和热误差同步测量。温度测量通过数字传感器DS18B20(测量精度为±0.2 ℃，最高分辨率达0.0625 ℃)进行。实验采用电感位移传感器对Z向热误差进行测量，电感式位移传感器的测量精度为±0.5μm。实验过程中，工作台保持不动，主轴以恒定转速(1000r/min、2000r/min、3000r/min、4000r/min)转动，每隔3min采集一次温度和热误差数据，持续时间在4h以上。实验数据参数如表2所示，K1～K7批次数据的热误差数据如图2所示。

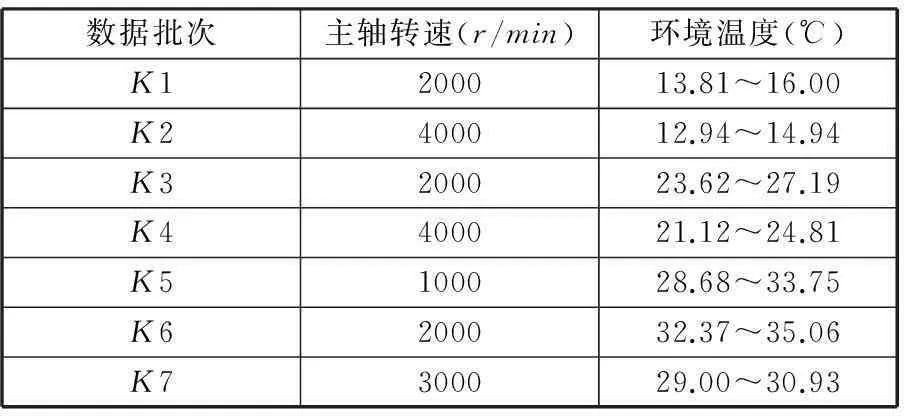
表2　实验数据参数

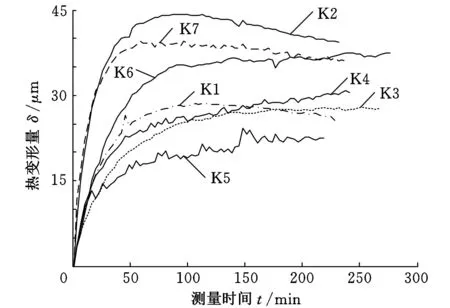
图2　K1～K7批次的热误差数据

3温度敏感点变动性及其影响

3.1温度敏感点变动性分析

采用模糊聚类结合灰色关联度的方法[12-13]计算K1～K7批次数据的温度敏感点，结果如表3所示。由表3可知，K1、K2、K4、K5、K6批次数据的温度敏感点位置在主轴前轴承和主轴电机位置处，但K3批次数据的温度敏感点都在主轴电机处，K7批次的温度敏感点在主轴前轴承和机床外壳(T10)处。各数据的温度敏感点计算结果不完全相同，即热误差补偿模型所依据的温度敏感点位置存在变动性特征。

表3　温度敏感点计算结果

经分析，温度敏感点变动性直接来源于数控机床热源的波动性，其变动性规律尚缺少研究。影响热源波动性的因素较为复杂，与机床结构特性、工作参数变化、环境温度等密切相关。那么，温度敏感点位置的变动是否对回归模型精度产生影响呢？需要展开讨论。

3.2温度敏感点变动对模型精度影响

实际数控机床热误差补偿应用时，常根据一次实验测量数据建立补偿模型，故模型自变量应为各数据自身的敏感点变量。

以各数据的敏感点变量为模型自变量，分别建立K1～K7批次数据的多元线性回归(MLR)模型。K1～K7批次数据的MLR模型分别如下：

(5)

式中，ΔTi为温度传感器Ti的温度值增量；yi为Ki批次数据的模型热误差预测值。

根据上述建立的K1～K7批次数据的MLR模型，对K1～K7批次数据进行拟合及预测精度分析，如表4所示。其中，拟合精度是指根据历史数据所建立的模型，对建模的历史数据的偏离程度的评价。预测精度是指根据历史数据所建立的模型，对未参与建模的历史数据的偏离程度的评价[12-13]。表4中，Mi(i=1,2,…,7)为根据Ki批次数据建立的MLR模型；黑体数字为模型拟合标准差，非黑体数字为模型预测标准差。

表4　MLR模型拟合及预测效果　μm

由表4可知，MLR模型的拟合标准差分布范围为0.67～2.17 μm,预测标准差的分布范围为2.54～36.61 μm。由于建模时使用的是各批次数据自身的敏感点变量，故模型的拟合精度非常高；而模型的预测精度时高时低，预测稳健性不强，则是由于预测数据的温度敏感点发生了变动，导致模型自变量多重共线性发生变化，对模型的预测稳健性产生了严重影响。因此需要采用一种数学算法来控制敏感点变动性造成的模型预测精度损失。

主成分回归算法可消除自变量共线性影响，故下文将利用该算法建立热误差模型，并对其模型精度进行分析。

4主成分回归建模及精度分析

4.1主成分回归建模

首先介绍主成分回归算法的计算步骤。

R的特征值和特征向量如表5所示。

表5　特征值和特征向量

根据式(1)得到主成分Z1和Z2的表达式分别为

(6)

由式(2)求主成分Z1和Z2的累计贡献率分别为96.325%和100%，可知，Z1的累积贡献率达到96.3250%≥85%，故取主成分个数g=1。

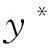
(7)

方程中只包含一个主成分，不存在共线性问题。当方程中存在多个主成分时，通过计算也会发现，这些主成分之间具有不相关性。

将式(6)中第一式代入式(7)得

(8)

根据式(4)将式(8)还原到原始数据y1关于ΔT1、ΔT8的主成分回归方程：

y1=11.8384+1.5252ΔT1+1.9669ΔT8

(9)

重复上述步骤，计算得到K2～K7批次数据的PCR模型如下:

(10)

4.2PCR模型精度分析

根据上述建立的K1～K7批次数据的PCR模型，对K1～K7批次数据进行拟合及预测精度分析，结果如表6所示。表6中，Mi(i=1,2,…,7)为根据Ki批次数据建立的PCR模型(为便于下文的比较，本文将根据Ki批次数据建立的MLR模型和PCR模型均取名为Mi)；黑体数字为模型拟合标准差，非黑体数字为预测标准差。

表6　PCR模型拟合及预测效果　μm

由表6可知，PCR模型的拟合标准差分布范围为2.33～5.07 μm，预测标准差分布范围为2.56～12.45 μm。

4.3PCR和MLR模型精度的综合比较

通过对表4和表6中的标准差数据进行进一步分析，得到K1～K7批次数据的MLR模型和PCR模型的拟合效果和预测效果，如表7所示。其中，S为评判拟合精度的参数，其值越小，说明模型拟合精度越高；Mn为评判预测精度平均水平的参数，其值越小，说明模型的平均预测精度越高；Sd为评判预测精度离散程度的参数，其值越小，说明模型预测的稳健性越强。Mn、Sd的计算式分别为

式中，sri(i=1,2,…,6)为各模型的6个预测标准差。

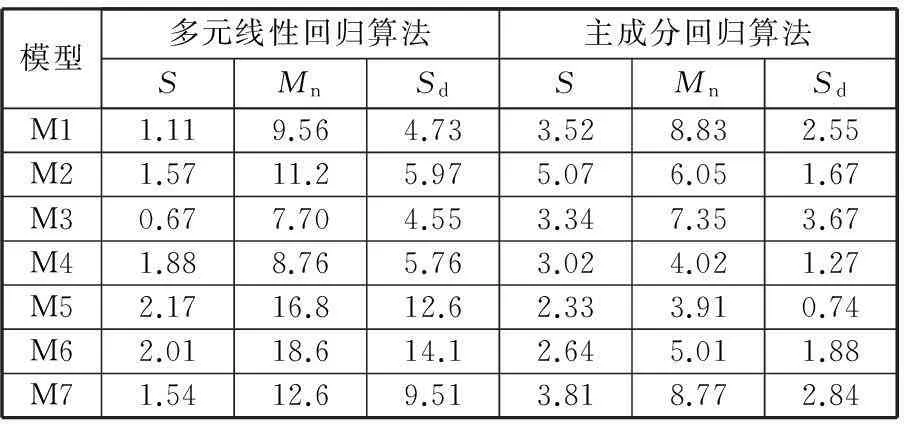
表7　模型拟合及预测效果分析　μm

将表7中数据以二维直方图形式表示，分别如图3～图5所示。

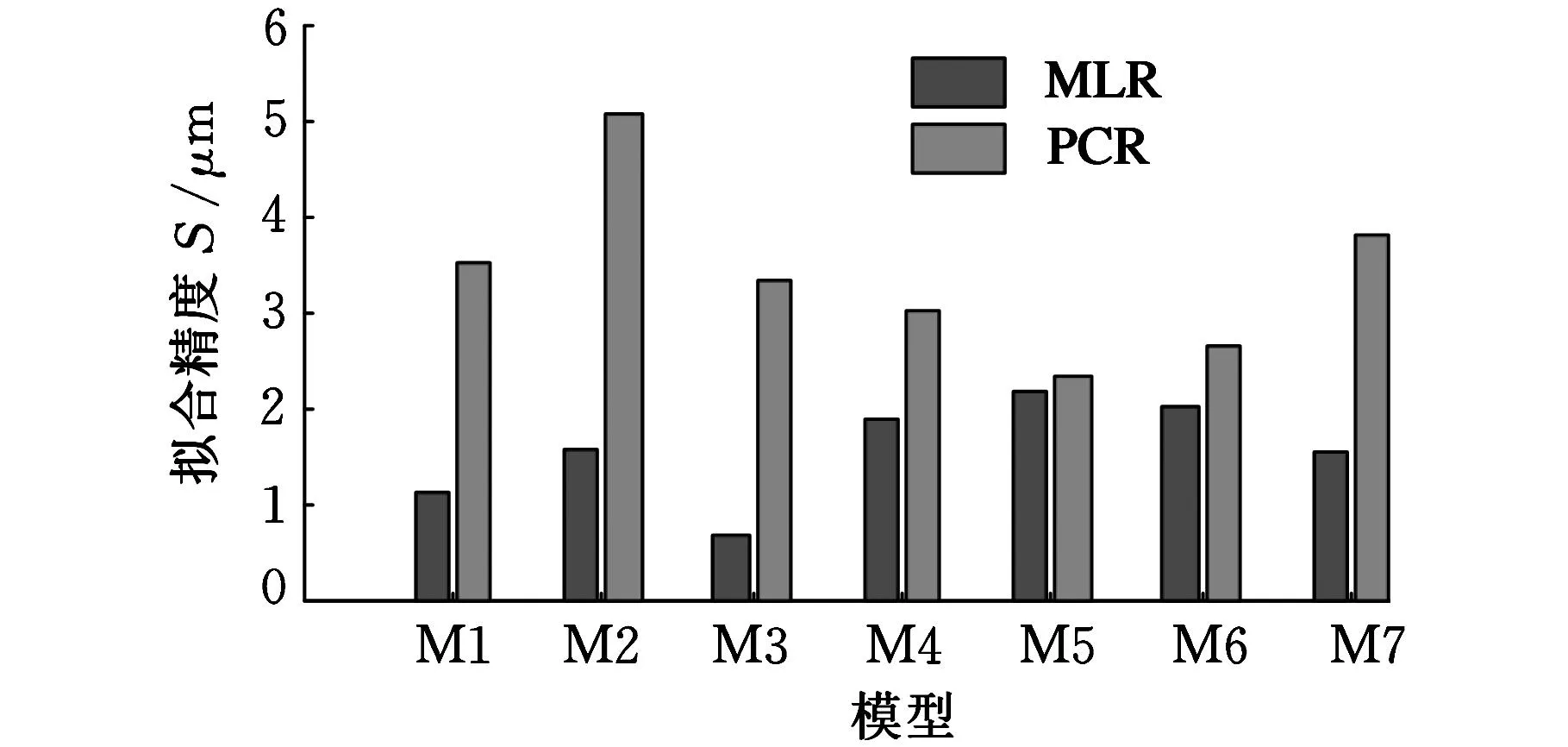
图3　MLR模型和PCR模型的拟合效果比较

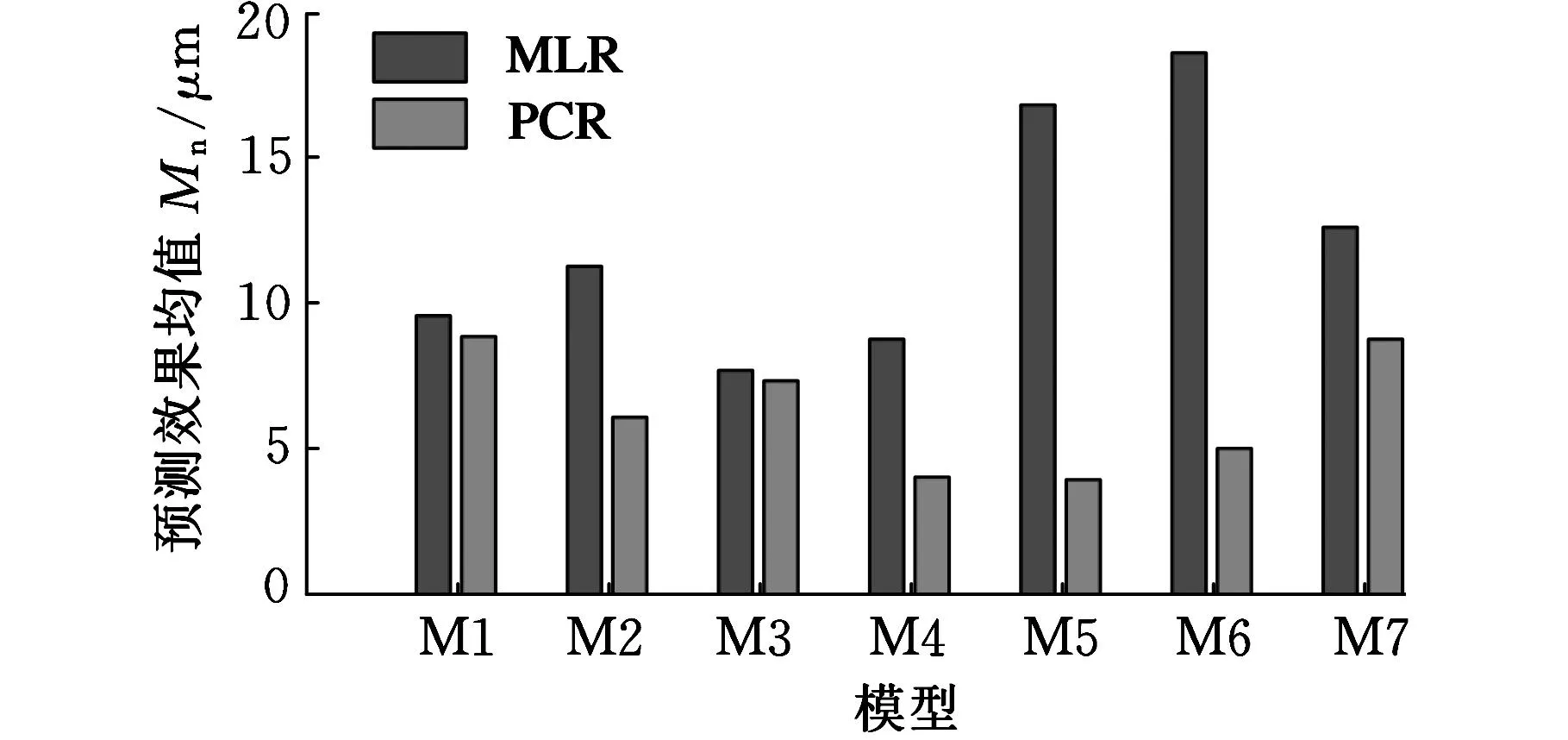
图4　MLR模型和PCR模型的预测效果均值比较

图5　MLR模型和PCR模型的预测效果标准差比较

综合表7和图3～图5，得到MLR模型和PCR模型的拟合效果范围、预测效果均值范围和预测效果标准差范围如表8所示。

表8　模型拟合效果及预测效果范围　μm

由表8可知，PCR模型的整体拟合效果低于MLR模型的整体拟合效果，但PCR模型的整体预测效果远远高于MLR模型的整体预测效果。究其原因，是因为主成分回归算法消除了自变量间共线性影响，很好地抑制了敏感点变动对模型预测稳健性产生的影响，使得模型精度和预测稳健性大幅度提高，但其算法本身的训练精度要稍微低于MLR算法，所以模型拟合精度略低。

然而实际机床热误差补偿应用时，是利用事先计算好的数学模型对之后的机床运行状态进行补偿，因此更偏重模型预测效果的好坏。故温度敏感点发生变动时，主成分回归算法可以明显降低其对模型精度影响，保证模型具有较好的预测精度和稳健性。

5结论

(1)本文对Leaderway-V450数控加工中心主轴Z向进行了多组热误差空转实验，并采用模糊聚类结合灰色关联度的方法对温度数据进行了温度敏感点分析。结果表明，热误差补偿模型所依据的温度敏感点位置存在变动性特征，造成模型自变量间多重共线性发生变化。通过多元回归模型的精度分析，验证了温度敏感点变动会严重影响模型的预测稳健性。

(2)考虑到多重共线性对回归分析有严重影响，故本文提出采用具有消除共线性影响功能的主成分回归建模方法，并通过实际机床空转数据给予验证。结果表明，采用主成分回归算法建模，显著降低了温度敏感点变动对模型稳健性精度的影响。

本文结论只针对Leaderway-V450型数控加工中心，而对不同类型数控机床并未给予深入研究，故实验结果具有一定局限性。

参考文献：

[1]Bryan J B．International Status of Thermal Error Research[J]．Ann. CIRP,1990，39(2):645-656．

[2]Aronson R B．War against Thermal Expansion[J]．Manuf. Eng.,1996，116(6):45-50．

[3]Yang S，Yuan J，Ni J.Accuracy Enhancement of a Horizontal Machining Center by Real-time Error Compensation[J]．Journal of Manufacturing Systems，1996，15(2):113-124．

[4]Miao Enming，Gong Yayun，Niu Pengcheng，et al．Robustness of Thermal Error Compensation Modeling Models of CNC Machine Tools[J]. International Journal of Manufacturing Technology，2013，69(9)：2593-2603．

[5]倪军．数控机床误差补偿研究的回顾及展望[J].中国机械工程，1997，8(1):29-33．

Ni Jun．Review and Forecast for Thermal Errors Compensation of Machine Tools[J].China Mechanical Engineering，1997，8(1):29-33．

[6]Fan Jinmei．Sensor Placement Strategy for Thermal Error Compensation on Machine Tools[J].Chinese Journal of Scientific Instrument,2005：83-84．

[7]Attia M H，Fraser S．A Generalized Modeling Methodology for Optimized Real-time Compensation of Thermal Deformation of Machine Tools and CMM Structures[J]．International Journal of Machine Tools & Manufacture，1999，39(6)：1001-1016．

[8]LoC，YuanJ，NiJ．AnapplicationofReal-timeErrorCompensationonaTurningCenter[J]．InternationalJournalofMachineTools&Manufacture，1995，35(12)：1669-1682．

[9]LoC，YuanJ，NiJ．OptimalTemperatureVariableSelectionbyGroupingApproachforThermalErrorModelingandCompensation[J].Int.J.Mach.ToolsManufact., 1999， 39(9):1383-1396．

[10]LeeJ，YangS．StatisticalOptimizationandAssessmentofaThermalErrorModelforCNCMachinetools[J].InternationalJournationofMachineTools&Manufacture，2002，42(1)：147-155．

[11]杨建国，邓卫国，任永强，等．机床热补偿中温度变量分组优化建模[J].中国机械工程，2004，15(6)：478-481．

YangJianguo，DengWeiguo，RenYongqiang，etal．GroupingOptimizationModelingbySelectionofTemperatureVariablesfortheThermalErrorCompensationonMachineTools[J].ChinaMechanicalEngineering，2004，15(6)：478-48．

[12]苗恩铭，龚亚运，成天驹，等．支持向量回归机在数控加工中心热误差建模中的应用[J]. 光学精密工程，2013，21(4)：980-986．

MiaoEnming，GongYayun，ChengTianju，etal．ApplicationofSupportVectorRegressiontoThermalErrorModelingofMachineTools[J].OpticsandPrecisionEngineering，2013，21(4)：980-986．

[13]MiaoEnming，NiuPengcheng，FeiYetai，etal．SelectingTemperature-sensitivePointsandModelingThermalErrorsofMachineTools[J]．J.Chin.Sco.Mech.Eng.,2014，32(6):559-565．

[14]吴诚鸥，秦伟良．近代实用多元统计分析[M].北京：气象出版社，2007．

(编辑苏卫国)

Variability of Temperature-sensitive Points and Its Influences for CNC Machine Tools

Miao EnmingLiu YiGao ZenghanLiu Hui

Hefei University of Technology,Hefei,230009

Abstract：In thermal error compensation technology on CNC machine tools, the core issue was to establish mathematical model which might reflect the relationship between incremental temperature and thermal errors of the machine, and the accuracy and robustness of model depended on whether model’s independent variables could reflect the temperature field distribution of CNC accurately, in other words, whether the temperature-sensitive points were accurate and stable. The variability of temperature-sensitive points was proved by analyzing batches of experimental data of air cutting experiments on Leaderway-V450 machine tool spindle Z direction, so it changed the degree of multi-collinearity among temperature variables, caused a serious impact on model’s forecasting accuracy and robustness. Since PCR algorithm might eliminate the influences of multi-collinearity among variables, the modeling method was proposed based on PCR algorithm. And this method was used to practice tests through the experiments of actual machine. The results show, PCR model reduces the effects of changes in temperature-sensitive points on model’s forecasting accuracy significantly, and the model has good forecasting accuracy and robustness.

Key words:CNC machine tool; temperature-sensitive point; multi-collinearity; principal component regression(PCR)

收稿日期：2015-04-20

基金项目：国家自然科学基金资助重大项目(51490660，51490661)；国家自然科学基金资助项目(51175142，E051102)

中图分类号：TG502.15; TH161

DOI：10.3969/j.issn.1004-132X.2016.03.001

作者简介：苗恩铭，男，1971年生。合肥工业大学仪器科学与光电工程学院教授、博士研究生导师。主要研究方向为精密机械工程、精度理论、数控机床热误差补偿、机械热鲁棒性结构设计理论与应用技术。出版专著1部，发表论文50余篇。刘义，男，1994年生。合肥工业大学仪器科学与光电工程学院硕士研究生。高增汉，男，1990年生。合肥工业大学仪器科学与光电工程学院硕士研究生。刘辉，男，1991年生。合肥工业大学仪器科学与光电工程学院硕士研究生。