基于小波半软阈值消噪的盲源分离方法

孟　宗　马　钊　刘　东　李　晶

1.河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，0660042.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004

基于小波半软阈值消噪的盲源分离方法

孟宗1,2马钊1刘东1李晶1

1.河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，0660042.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004

摘要：为了有效提取含噪机械故障信号中的故障特征信息，研究了一种基于小波半软阈值消噪的盲源分离方法。利用小波半软阈值对故障信号进行消噪处理；采用联合近似对角化算法对信号进行盲源分离；考虑在噪声干扰下预消噪常常不足以消除全部噪声，因此在盲源分离后再进行适当的消噪处理，以提高其分离性能。实验验证了所提出方法的有效性和可行性。

关键词：盲源分离；小波；半软阈值；故障诊断

0引言

盲源分离(blind source separation, BSS)是指在源信号和传输通道参数未知的情况下，依据输入源信号的统计特性，仅由观测信号恢复出源信号各个独立成分的过程[1]。近年来，盲源分离已经成为一个非常热门并被广泛研究的新型信号处理技术。人们在盲源信号分离上做出了很多有成效的研究，盲源分离在机械[2-5]、通信[6]、语音[7]和生物医学[8]等领域得到迅速的发展和推广。

旋转机械设备结构复杂，干扰源较多。传感器安装在机械设备上时，采集到的观测信号通常是各个振动源信号通过未知的传输路径，连同干扰和噪声以不同方式组合而成。理想的盲源分离方法常常忽略噪声的影响或者把噪声当作一个独立的源信号。在高阶统计方法中，由于Gauss信号的高阶累积量为零，所以可以假设加性Gauss噪声存在。若忽略噪声的影响而直接进行盲源分离，则信号分离效果往往很差[9-10]。因此，基于盲源分离的机械故障诊断中必须考虑噪声的影响。Donoho[11]提出了小波阈值消噪方法，该方法简单，计算量小，应用比较广泛。在基于小波变换和盲源分离的机械故障诊断中，人们常常在盲源分离之前进行小波消噪预处理[12-14]，常用的小波阈值消噪方法包括硬阈值消噪法和软阈值消噪法，但是这两种方法自身都有缺陷，因此，合适的阈值函数是小波阈值消噪法中很重要的因素。本文将小波半软阈值消噪与盲源分离相结合，利用小波半软阈值对故障信号进行消噪，然后基于联合近似对角化算法对信号进行盲源分离，盲源分离后再进行适当的消噪处理，以提高其分离性能。

1小波半软阈值消噪

在小波阈值消噪法中，阈值函数的选取是一个关键。硬阈值和软阈值消噪方法虽然在实际中得到了广泛应用，但其本身存在许多缺点。

(1)硬阈值方法公式为

^ωj,k=ωj,k |ωj,k|≥λ0 |ωj,k|<λ{

(1)

k=0,1,2,…,n-1j=0,1,2,…,J

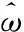
(2)软阈值方法公式为

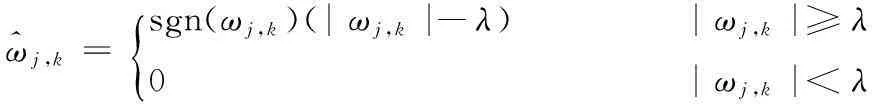
^ωj,k=sgn(ωj,k)(|ωj,k|-λ) |ωj,k|≥λ0 |ωj,k|<λ{

(2)

(3)针对上述软阈值、硬阈值方法的不足，本文给出小波半软阈值算法[15]，其阈值函数为

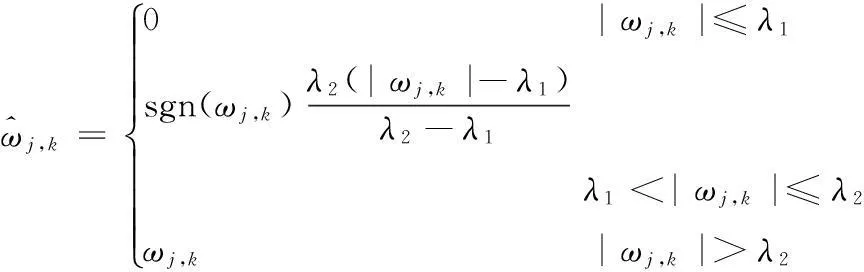
^ωj,k=0 |ωj,k|≤λ1sgn(ωj,k)λ2(|ωj,k|-λ1)λ2-λ1 λ1<|ωj,k|≤λ2ωj,k |ωj,k|>λ2ìîíïïïïïï

(3)

式中，λ1、λ2为给定的阈值。

当λ1<|ωj,k|≤λ2时，接近软阈值；当|ωj,k|>λ2时，与硬阈值相同；当λ1=λ2时，为硬阈值法；当λ2=∞时，为软阈值法。

为了验证小波不同阈值函数下的消噪效果，构造一个轴承振动仿真信号，其表达式为

x(t)=sin(2πf1t)(1+0.1sin(2πf2t))

(4)

式中，f1为轴承中滚子通过内圈的特征频率,f1=150Hz；f2为旋转频率,f2=20Hz。

x(t)的波形如图1所示，添加随机白噪声后波形如图2所示。

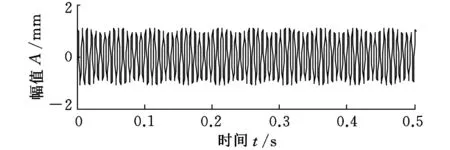
图1　源信号

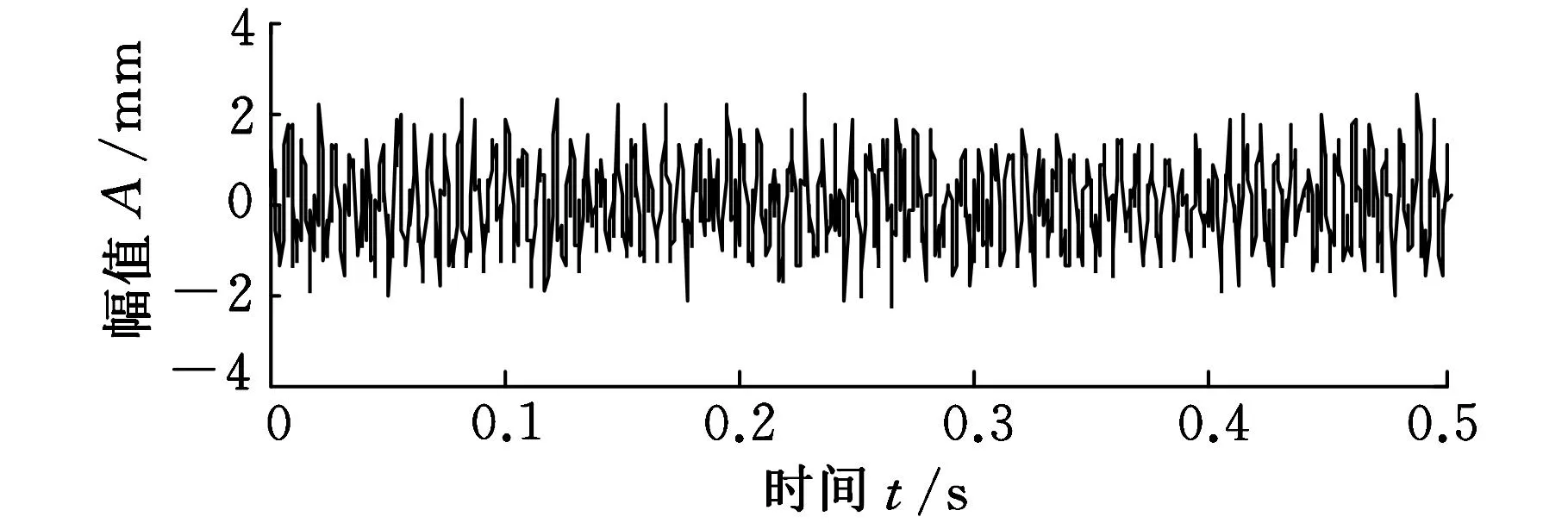
图2　含噪信号

对x(t)进行小波阈值消噪处理，小波函数选取dB5小波，分解层数选取5层，阈值规则选择rigrsure规则，分别使用硬阈值法、软阈值法和半软阈值法进行消噪处理，消噪效果如图3～图5所示。

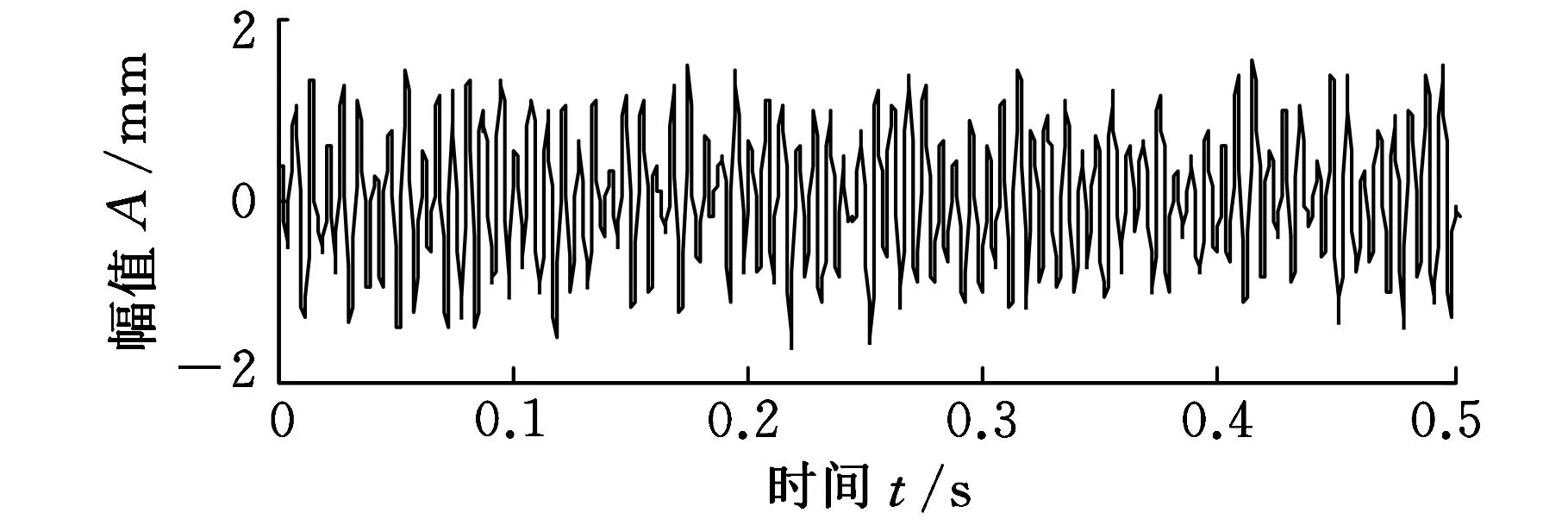
图3　硬阈值消噪

图4　软阈值消噪

图5　半软阈值消噪

衡量信号去噪效果的重要指标主要有均方根误差(root-mean-square error,RMSE)和信噪比(signal to noise ratio,SNR)，表1分别给出了不同阈值函数处理后的均方根误差和信噪比。小波消噪前，含噪信号的信噪比为2.2553，小波半软阈值消噪后信噪比为8.1851，高于小波硬阈值消噪的5.6930以及小波软阈值消噪的5.7228，并且小波半软阈值消噪后信号的均方根误差最小，这表明半软阈值法能更好地降低均方根误差，同时可提高信噪比，从而有效地抑制了噪声，使降噪信号更接近原信号。

表1　三种阈值法消噪效果比较

2基于小波半软阈值消噪的盲源分离

在含噪的线性瞬时混合模型里，源信号和观测信号的关系可以描述为

y(t)=As(t)+n(t)

(5)

其中，y(t)=(y1(t),y2(t),…,yM(t))T，为含噪情况下的M维随机观测向量； s(t)=(s1(t),s2(t),…,sN(t))T，为N维源信号向量，并且假设源信号中各分量si(t)为统计独立的；A为一个未知满秩的M×N的混合矩阵；n(t)=(n1(t)n2(t),…,nM(t))T为M维加性观测噪声，且M≥N。

含噪盲源分离问题是指，在混合矩阵A以及源信号s(t)均未知的情况下，仅根据观测信号y(t)确定分离矩阵W，从而获得对未知源信号s(t)的估计。设s′(t)为源信号的估计向量，则分离系统输出的数学模型为

s′(t)=Wy(t)=WAs(t)+Wn(t)

(6)

显然，式(6)中Wn(t)将增大分离结果s′(t)的方差，因此在强烈的噪声环境下，若想提高分离性能，则需要先对信号进行消噪处理。为了消除噪声信号的干扰，提高盲源分离的分离效果，在对含噪观测信号进行盲源分离前，先进行小波半软阈值消噪，然后使用联合近似对角化算法[16]进行盲源分离。预消噪常常不足以消除全部噪声，因此最后再对分离后的信号进行小波半软阈值消噪后处理。此过程如图6所示。

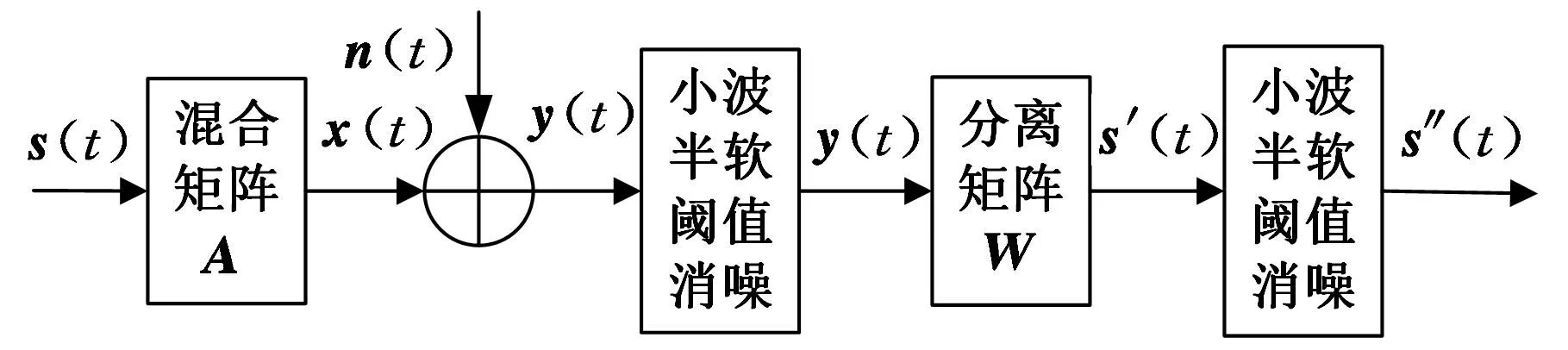
图6　基于小波半软阈值消噪的盲源分离流程

为了验证小波半软阈值盲源分离的分离效果，构建以下信号进行仿真：

s1=3sin12πtcos120πt

(7)

s2=sin80πt(1+0.5sin180πt)

(8)

s3=sin20πt+sin60πt

(9)

其中，采样频率为1000 Hz，采样长度为1024。根据线性瞬时混合盲源分离模型式(5)，将s与随机矩阵A混合，加上加性高斯白噪声，生成含噪的观测信号y(t)，源信号s(t)的波形如图7所示，观测信号y(t)的波形如图8所示。然后再使用基于不同的小波阈值消噪的盲源分离方法对y(t)进行分离，得到不同的分离效果。图9为小波硬阈值消噪盲源分离方法得到的分离效果图，图10为小波软阈值消噪盲源分离方法得到的分离效果图，图11为小波半软阈值消噪盲源分离方法得到的分离效果图，图12为小波半软阈值盲源分离后再进行小波半软阈值处理得到的效果图。

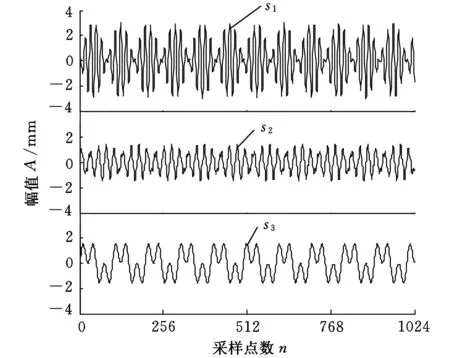
图7　源信号

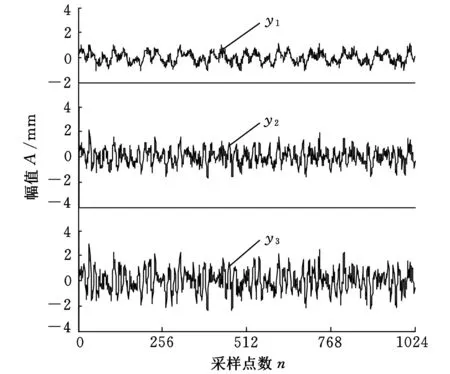
图8　观测信号

图9　小波硬阈值消噪盲源分离

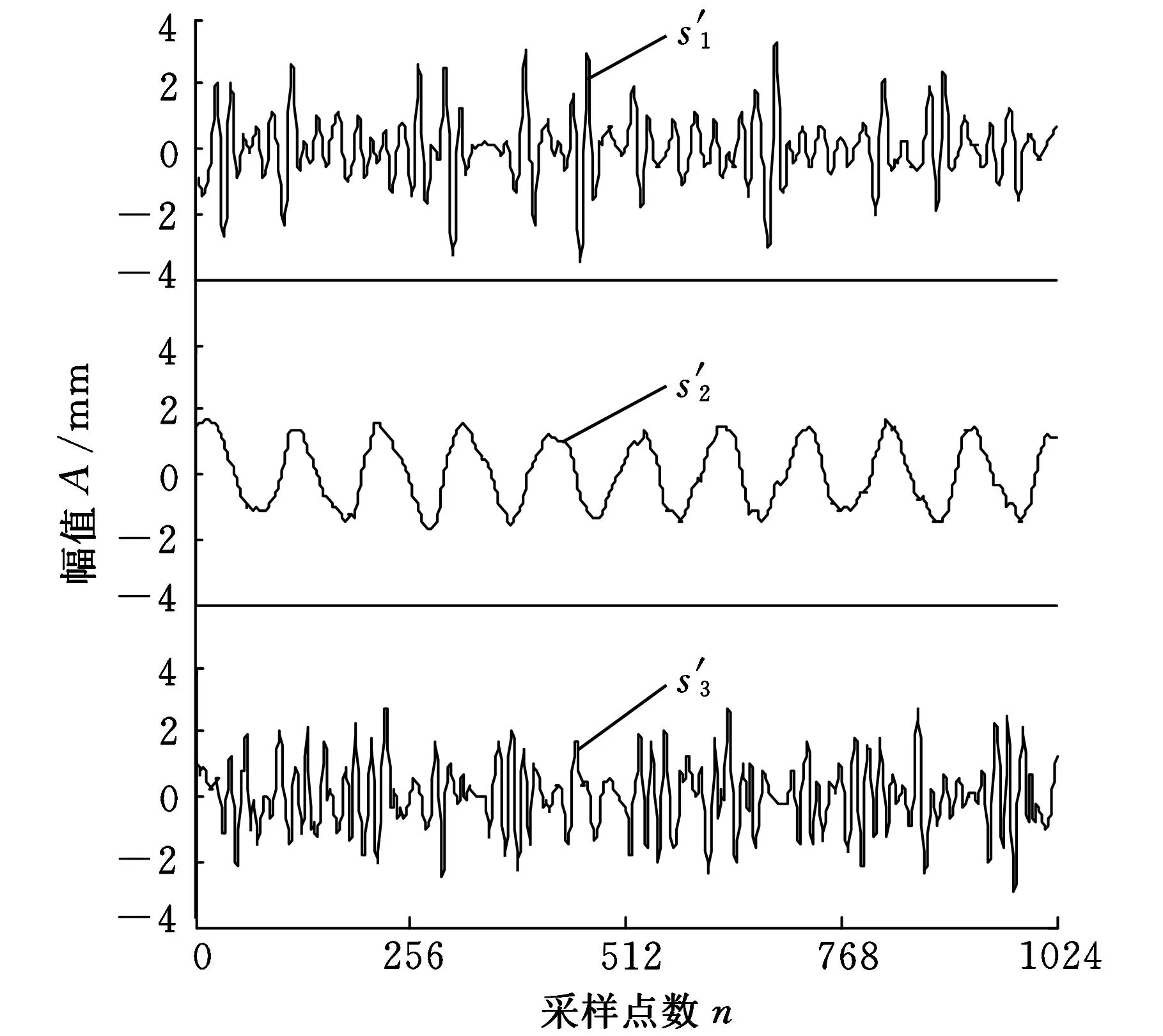
图10　小波软阈值消噪盲源分离

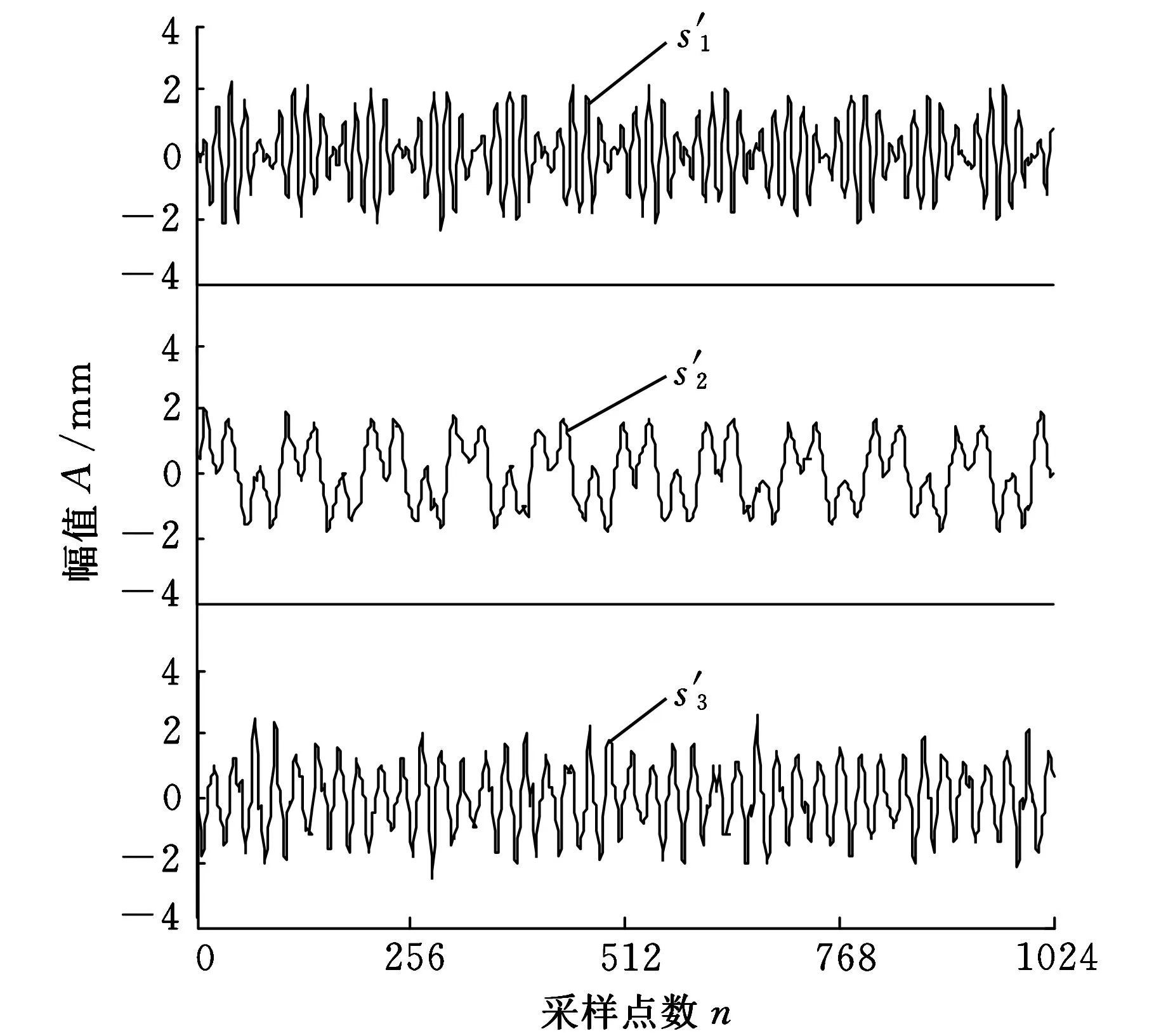
图11　小波半软阈值消噪盲源分离

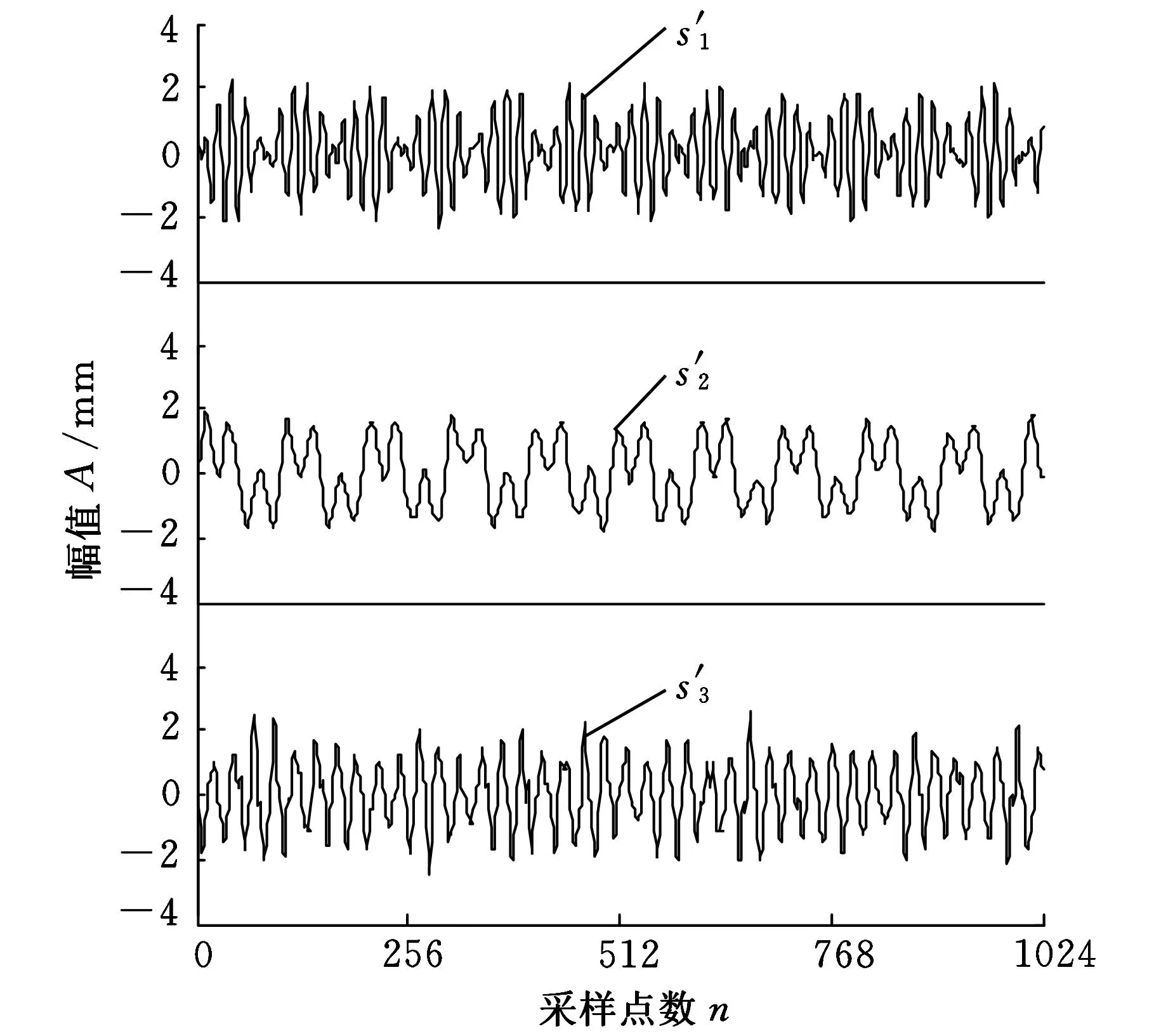
图12　小波半软阈值盲源分离后再次小波半软阈值消噪

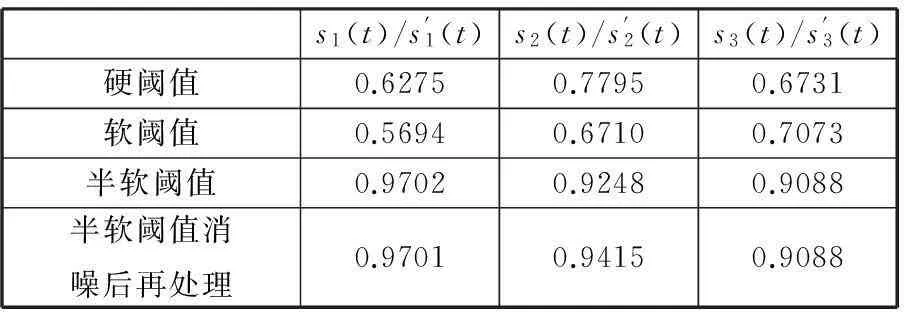
表2　不同阈值方法消噪盲源分离的相似系数

为了验证本方法分离后在频域上的效果，对图12进行幅值谱分析，得到的幅值谱如图13所示。

图13　幅值谱图

3实验研究

实验数据来源于西储大学旋转机械故障模拟试验台，被测试的轴承型号为6205-2RSSKF，是支撑电机转动轴的深沟球轴承。表3所示为测试所用轴承的规格参数。

表3　轴承规格参数

试验中，电机转速为1797r/min，采样频率为12kHz，采样长度为1024，使用电火花加工技术在轴承上布置了单点故障，故障直径为0.1778mm。根据轴承的结构尺寸和工作转速，可以计算出轴承内圈的故障特征频率fi=162.2 Hz，外圈故障特征频率fo=107.4 Hz。为了验证本文方法，分别取内圈和外圈故障信号的1024个点进行分析，将该轴承内圈和外圈的振动故障信号进行混合后，人为地加入干扰噪声，得到两个混合观测信号，混合观测信号的时域波形如图14所示。

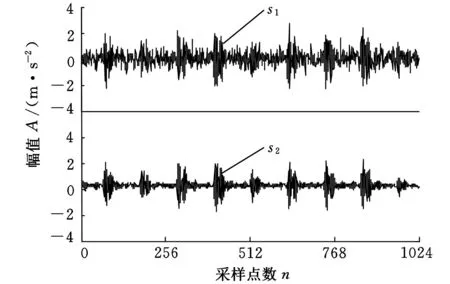
图14　混合观测信号

使用本文方法对观测信号进行处理，当使用幅值谱分析处理后的信号时，由于内圈、外圈特征频率与转频的和差规律作用[17]，它们产生的高频部分并不是所需的故障特征频率，这些频率只是轴承转频、外圈损伤、内圈损伤等引起的特征频率的整数倍之和或差值，需要对其进行包络解调，即进行包络谱分析。对观测信号进行本文方法的处理后得到的信号如图15所示。再对其进行包络谱分析，得到如图16所示的包络图。

图15　分离信号时域波形图

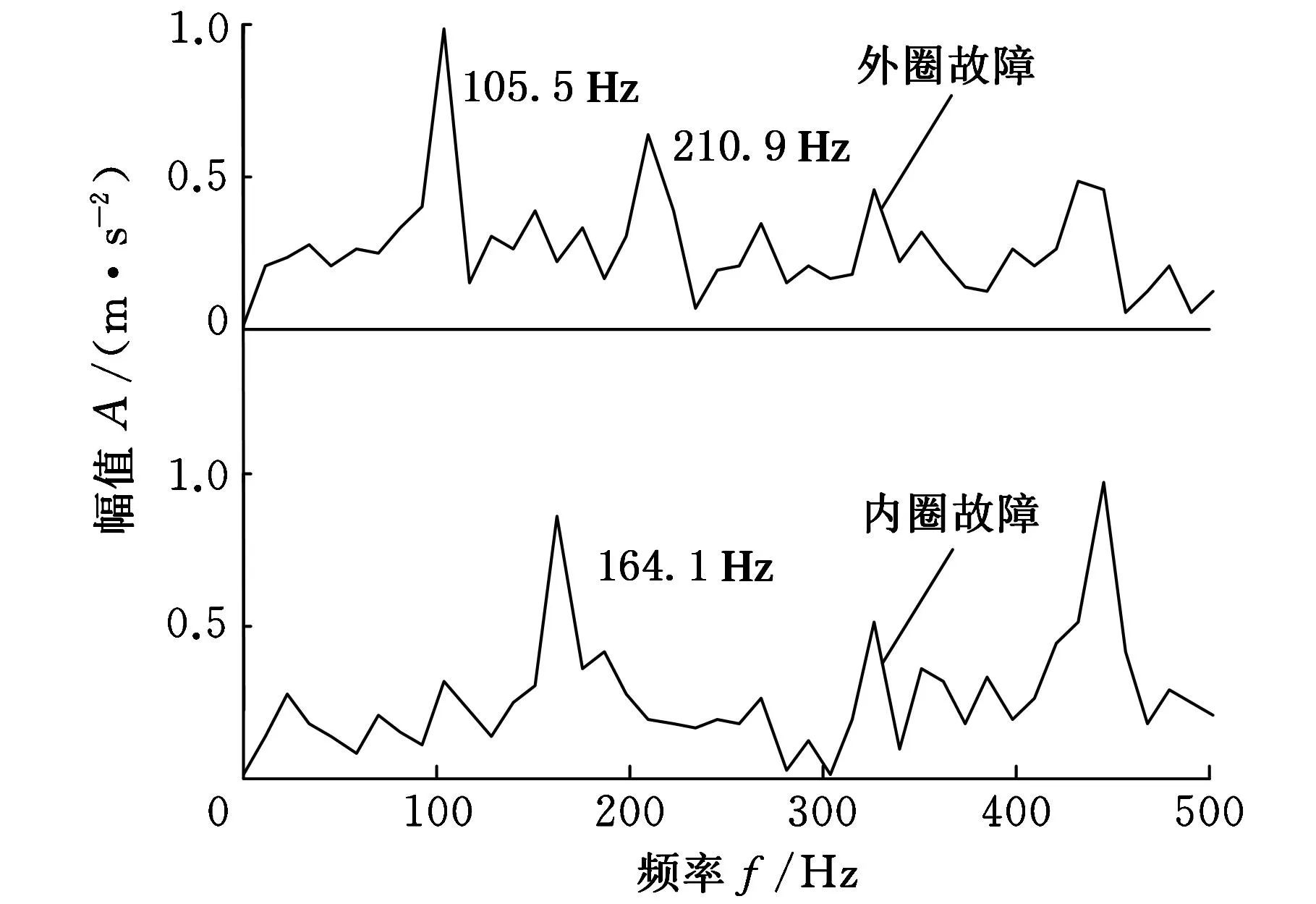
图16　分离信号的包络图

由图16可以看出，在105.5 Hz和210.9 Hz处出现了峰值，对应着外圈故障信号107.4 Hz和其二倍频；在164.1 Hz处出现了峰值，接近理论上内圈故障数据的162.2 Hz。同样情况下，也对观测信号进行了基于小波硬阈值和小波软阈值消噪的盲源分离，其结果不是很理想，没有有效地分离出源信号，并且其包络谱也无法反映出源信号的故障特征。基于小波半软阈值消噪预处理和后处理的盲源分离方法具有更好的分离效果。

4结语

基于盲源分离的机械故障信号分离中，噪声是一个需要考虑的重要因素，不消噪或者消噪效果不好都会导致分离出现较大偏差，从而无法有效地诊断出故障。通过仿真证明，小波半软阈值的消噪效果要好于小波硬阈值和小波软阈值，并且应用在盲源分离上时，小波半软阈值消噪-盲源分离的分离效果比小波硬阈值、软阈值消噪-盲源分离的分离效果要好，可以更加准确地还原源信号的波形，并且可以清晰地反映出源信号的特征频率，而再经过半软阈值后处理的波形和源信号会更加相似，效果会更好。应用实验数据，在添加噪声环境的情况下，本文方法很好地提取了旋转机械的振动信号内圈和外圈的故障特征频率，为噪声背景下应用盲源分离提供了一种方法。

参考文献：

[1]Leung C, Siu W. A General Contrast Function Based Blind Source Separation Method for Convolutively Mixed Independent Sources[J]. Signal Processing, 2007, 87(1):107-123.

[2]张洁, 高宏力, 陈春俊,等. 高速列车非平稳振动信号盲源分离方法及应用[J]. 机械工程学报, 2014, 50(19):97-104.

Zhang Jie, Gao Hongli, Chen Chunjun, et al. Blind Source Separation Method and Application for Nonstationary Vibration Signal of High Speed Train[J]. Journal of Mechanical Engineering, 2014, 50(19):97-104.

[3]李晓晖,傅攀.基于EEMD的单通道盲源分离在轴承故障诊断中的应用[J]. 中国机械工程, 2014, 25(7):924-930.

Li Xiaohui, Fu Pan. Application of Single-channel Blind Source Separation Based on EEMD in Bearing Fault Diagnosis[J]. China Mechanical Engineering, 2014, 25(7):924-930.

[4]杨宇,李永国,何知义,等. 基于LCD的齿轮箱混合故障盲源分离研究[J]. 中国机械工程,2015,26(8):1062-1066.

Yang Yu, Li Yongguo, He Zhiyi, et al. BSS Method of Gearbox Multi-fault Based on LCD[J]. China Mechanical Engineering, 2015, 26(8):1062-1066.

[5]韩春杨, 姚国凤, 赵建,等. 柴油机振动信号盲分离组合算法[J]. 振动与冲击, 2014, 33(6):44-47.

Han Chunyang, Yao Guofeng, Zhao Jian, et al. Combination Algorithm for Blind Separation of Diesel Engine Vibration Signal[J]. Journal of Vibration and Shock, 2014, 33(6):44-47.

[6]沈雷, 盛迪, 孙闽红,等. 单通道下基于盲源分离扩频通信抗干扰算法研究[J]. 电波科学学报, 2014, 29(5):923-927.

Shen Lei, Sheng Di, Sun Minhong, et al. Anti-jamming Algorithm of Spread Spectrum Communication Based on Blind Source Separation in Single Channel[J]. Chinese Journal of Radio Science, 2014, 29(5):923-927.

[7]夏秀渝, 何培宇. 基于声源方位信息和非线性时频掩蔽的语音盲提取算法[J]. 声学学报, 2013(2):224-230.

Xia Xiuyu, He Peiyu. Speech Blind Extraction Algorithm Based on Sound Source Azimuth Information and Nonlinear Time-frequency Masking[J]. Acta Acustica, 2013(2):224- 230.

[8]Pendharkar G, Naik G R, Nguyen H T. Using Blind Source Separation on Accelerometry Data to Analyze and Distinguish the Toe Walking Gait From Normal Gait in ITW Children[J]. Biomedical Signal Processing & Control, 2014, 13(5):41-49.

[9]刘晓平,郑海起,祝天宇.粒子滤波在含噪齿轮箱故障盲源分离中的应用[J]. 中国机械工程, 2011, 22(15):1853-1857.

Liu Xiaoping, Zheng Haiqi, Zhu Tianyu. Application of Particle Filter in Blind Source Separation of Gearbox Fault under Complex Noise Environment[J]. China Mechanical Engineering, 2011, 22(15):1853-1857.

[10]贾瑞生, 赵同彬, 孙红梅,等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015,58(3):1013-1023.

Jia Ruisheng, Zhao Tongbin, Sun Hongmei, et al. Micro-seismic Signal Denoising Method on Empirical Mode Decomposition and Independent Component Analysis[J].Chinese Journal of Geophysics, 2015, 58(3):1013-1023.

[11]Donoho D L. De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory,1995, 41(3): 613-627.

[12]罗志增,徐斌.基于小波消噪和盲源分离的脑电信号处理方法[J]. 华中科技大学学报(自然科学版), 2011, 39:157-160.

Luo Zhizeng, Xu Bin. EEG Signals Processed by Wavelet De-noising and Blind Source Separation[J]. J.Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2011, 39:157-160.

[13]Vázquez R R, Velez-Perez H, Ranta R, et al.Blind Source Separation, Wavelet Denoising and Discriminant Analysis for EEG Artefacts and Noise Cancelling[J]. Biomedical Signal Processing & Control, 2012, 7(4): 389-400.

[14]Zhang H B, Xu P F. Convolutive Blind Source Separation Based on Wavelet De-noising[J]. Advanced Materials Research, 2013,756-759:3356-3361.

[15]Gao HongYe, Bruce A G. Waveshrink with Semisoft Shrinkage. StatSci Research Report[R].Seattle: StatSci Division of MathSoft, Inc., 1995.

[16]Hyvarinen A, Oja E.A Fast Fixed-point Algorithm for Independent Component Analysis[J]. Neural Computation, 1997, 9(7):1483-1492.

[17]赵学智, 叶邦彦, 陈统坚. 基于小波—奇异值分解差分谱的弱故障特征提取方法[J]. 机械工程学报, 2012, 48(7):37-48.

Zhao Xuezhi, Ye Bangyan, Chen Tongjian. Extraction Method of Faint Fault Feature Based on Wavelet-SVD Difference Spectrum[J]. Journal of Mechanical Engineering, 2012, 48(7):37-48.

(编辑苏卫国)

Blind Source Separation Based on Wavelet Semi-soft Threshold Denoising

Meng Zong1,2Ma Zhao1Liu Dong1Li Jing1

1.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.National Engineering Research Center for Equipment and Technology of Cold Rolling Strip,Qinhuangdao,Hebei,066004

Abstract:In order to extract fault feature informations from the mechanical malfunction signals with noise, a method of blind source separation was proposed based on wavelet semi-soft threshold denoising. First, wavelet semi-soft threshold was used to filter the failure signals. Then, joint approximate diagonalization was used as blind source separation method to separate signals. Pretreatment was often not enough to eliminate all noises, therefore, it was necessary to denoise again to improve the separation performance. Finally, the feasibility and validity of this method was verified by experiments.

Key words:blind source separation; wavelet; semi-soft threshold; fault diagnosis

收稿日期：2015-04-15

基金项目：国家自然科学基金资助项目(51575472)；河北省自然科学基金资助项目 (E2015203356)；河北省高等学校科学研究计划资助重点项目(ZD2015049)；河北省留学人员科技活动择优资助项目(C2015005020)

中图分类号：TN911.7

DOI：10.3969/j.issn.1004-132X.2016.03.010

作者简介：孟宗，男，1977年生。燕山大学电气工程学院教授。主要研究方向为机械设备监测与故障诊断、振动信号分析与处理等。发表论文20余篇。马钊，男，1989年生。燕山大学电气工程学院硕士研究生。刘东，男，1990年生。燕山大学电气工程学院硕士研究生。李晶，女，1990年生。燕山大学电气工程学院硕士研究生。