旋转圆柱绕流的PIV实验研究
2016-06-23唐湛棋陈文义
孙 姣, 张 宾, 唐湛棋, 陈文义,*
(1. 河北工业大学 过程装备与控制工程系, 天津 300130; 2. 河北工业大学 工程流动与过程强化研究中心, 天津 300130; 3. 天津大学 力学系, 天津 300072; 4. 河北工业大学 力学系, 天津 300130)
旋转圆柱绕流的PIV实验研究
孙 姣1,2,3, 张 宾1,2, 唐湛棋2,4, 陈文义1,2,*
(1. 河北工业大学 过程装备与控制工程系, 天津 300130; 2. 河北工业大学 工程流动与过程强化研究中心, 天津 300130; 3. 天津大学 力学系, 天津 300072; 4. 河北工业大学 力学系, 天津 300130)
投弃式海流剖面仪(Expendable Current Profiler, XCP)周围流场是典型的旋转圆柱绕流。探头周围流场对探头的运动状态起决定性作用,这直接关系到探头的测量性能,因此有必要对旋转圆柱周围流场进行实验研究。实验在循环水槽中进行,通过PIV对雷诺数保持不变(Re=1000)、不同圆柱旋转速度比(α=0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5和5.0)的圆柱下游尾流场进行研究。通过选取不同旋转速度比的任一时刻的瞬态流场,来分析旋转对圆柱尾流结构的影响。为了获得流场的频率信息,对所获得流场信息进行能谱分析来获取涡旋的脱落频率, 并进一步使用正交模态分解对流场进行分析,给出了流场主要拟序结构及其能量与转速比的变化趋势。发现圆柱旋转改变圆柱尾流结构,使尾迹尺度变小。在旋转速度比0≤α≤2.0时,存在明显的周期性涡旋脱落,并且涡旋脱落的频率有逐渐升高的趋势;而且当转速比2.0<α≤5.0时尾迹流场的周期性减弱,涡旋脱落变得不明显,流场表现出低频、剪切层的区域特征。随着转速变大,涡旋尺度变小。在较高旋转速度比时,流场中能量被重新分布。
旋转圆柱;转速比;涡旋脱落频率;涡旋尺度;正交模态分解;PIV测量
0 引 言
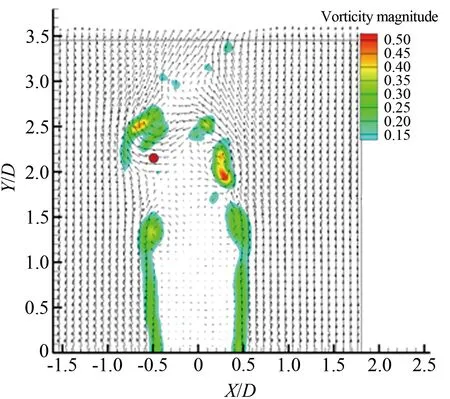
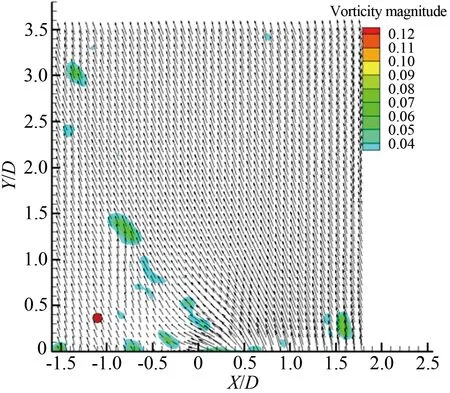
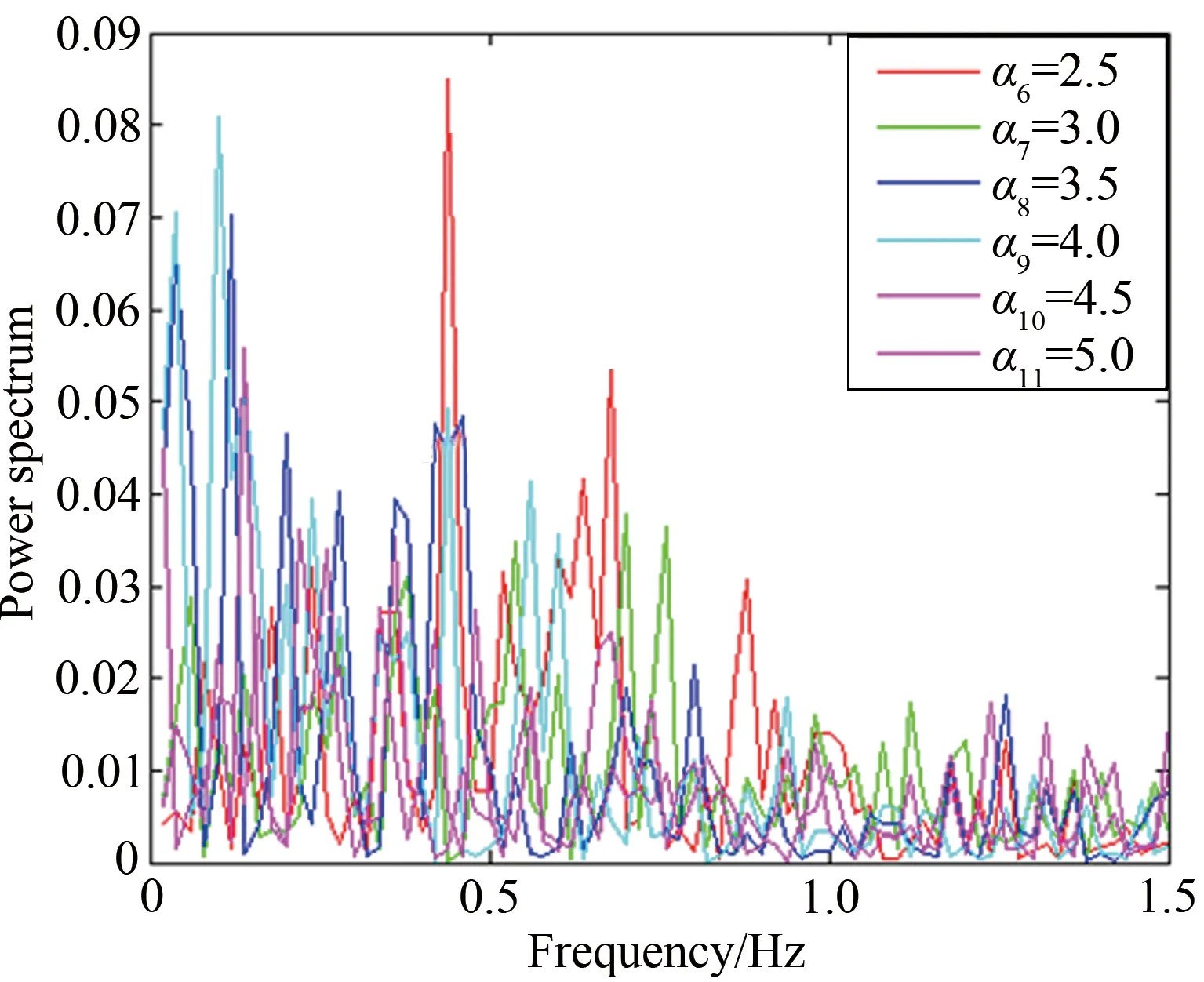
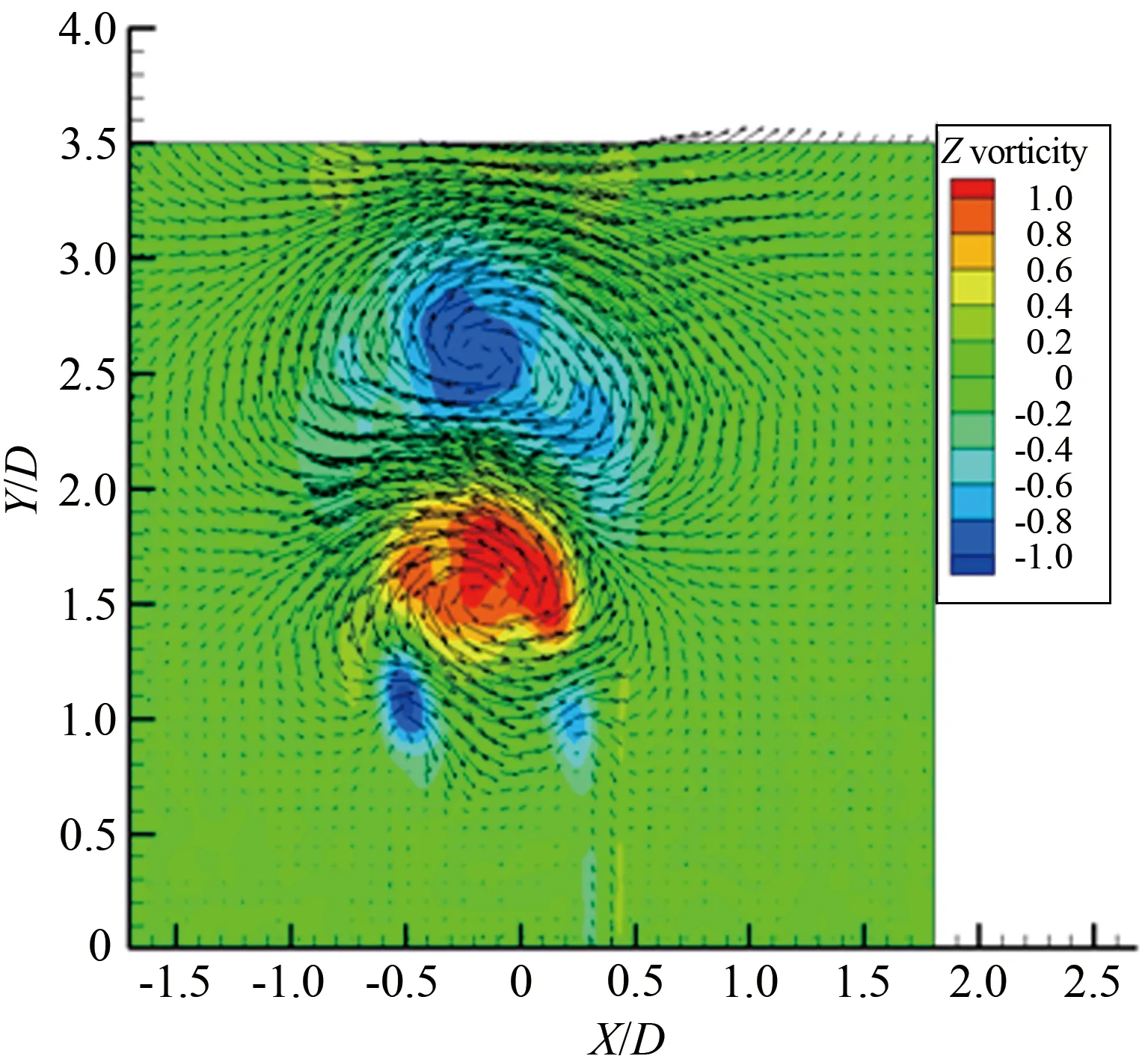
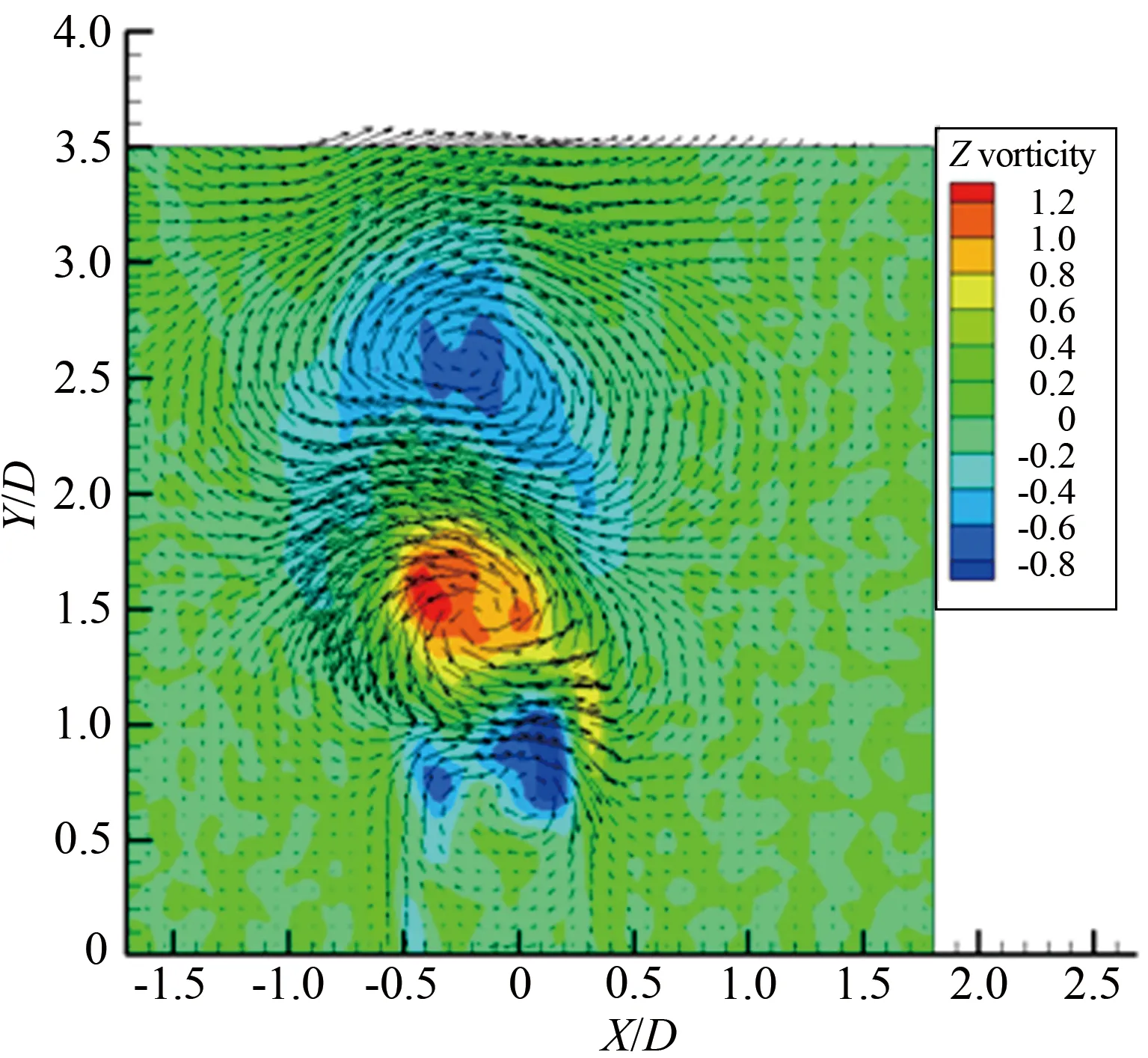
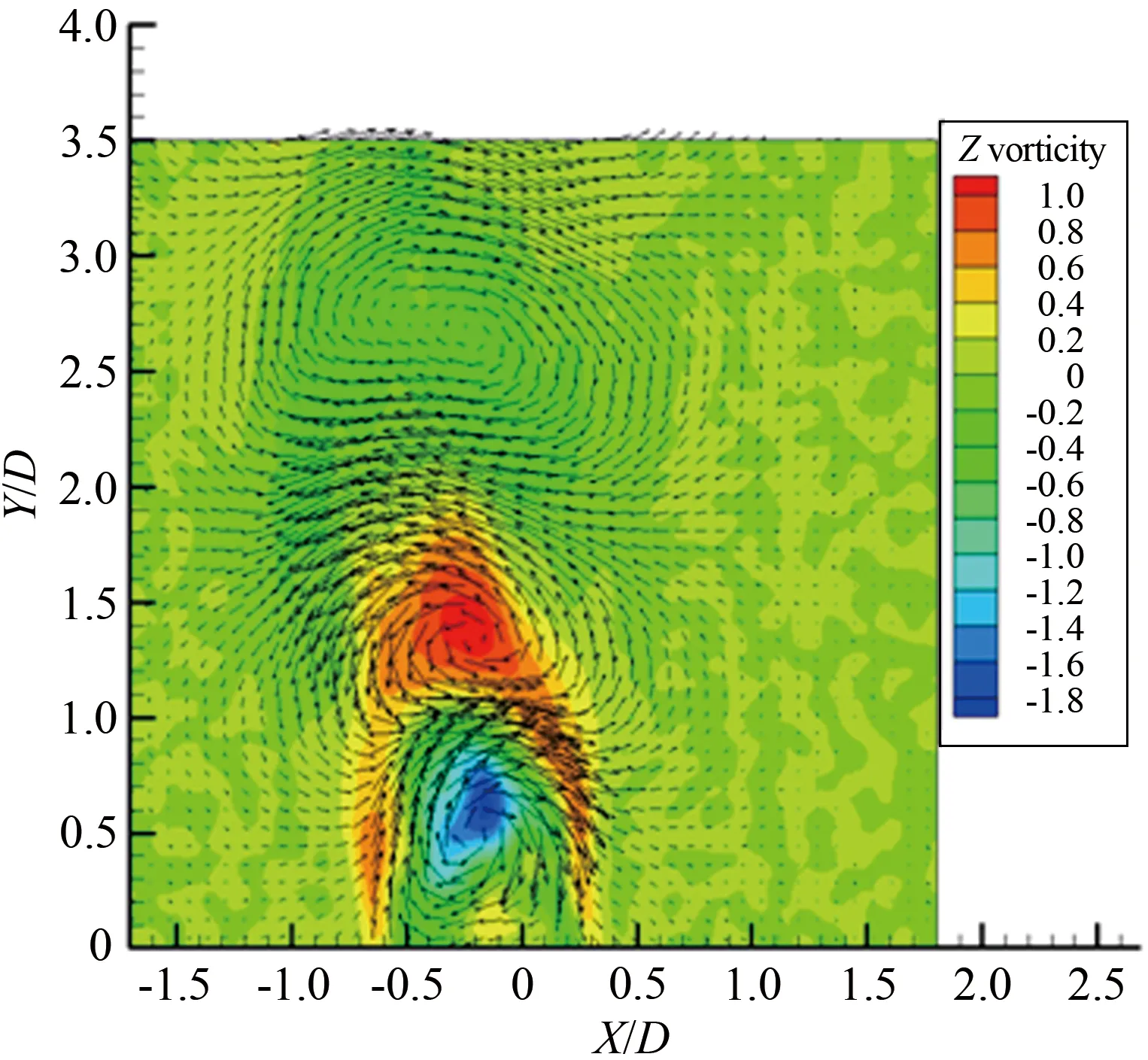
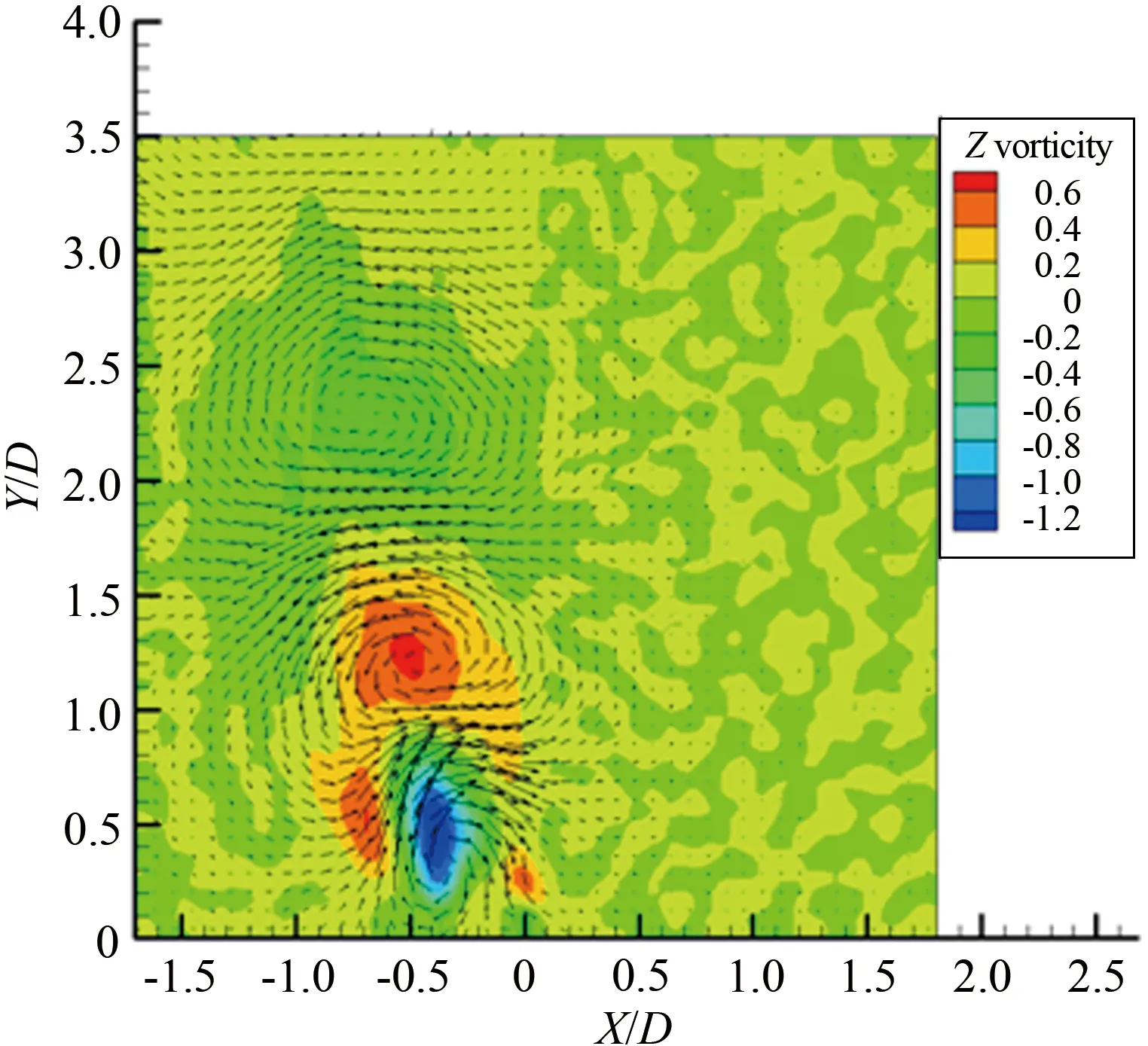
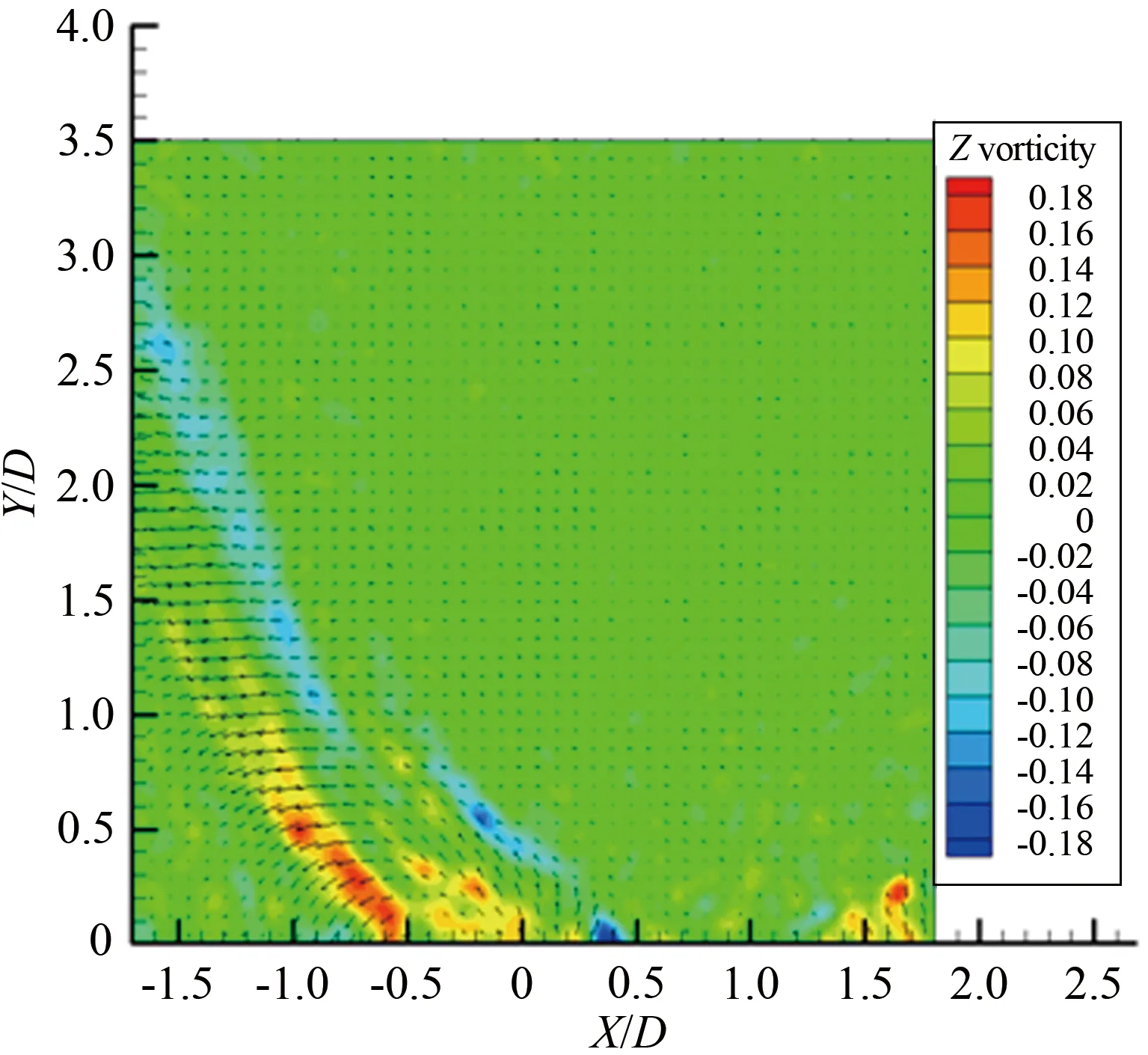
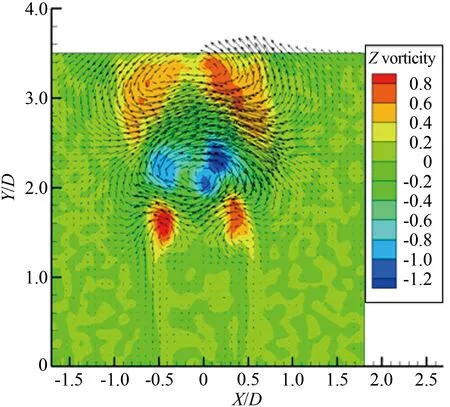
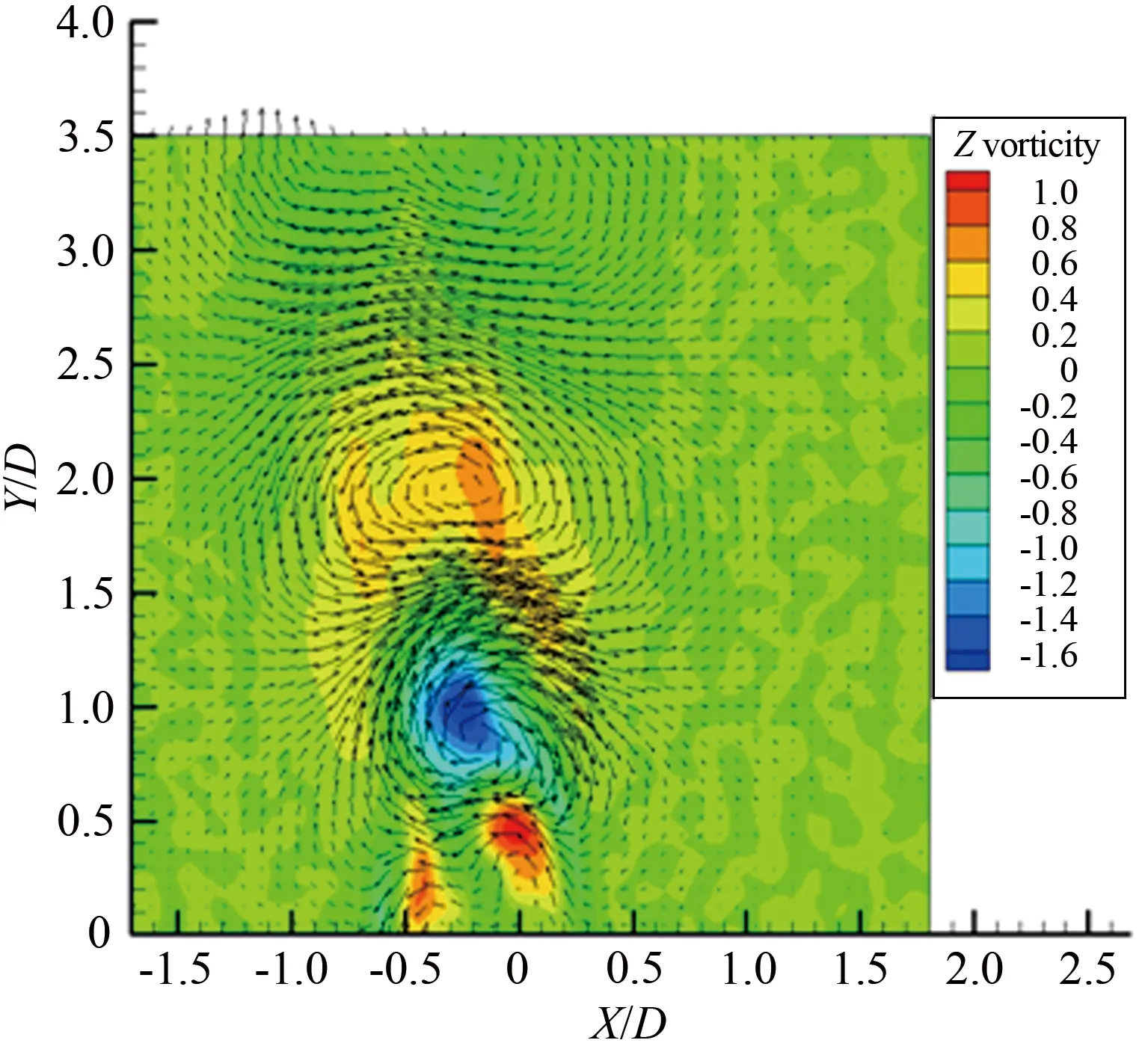
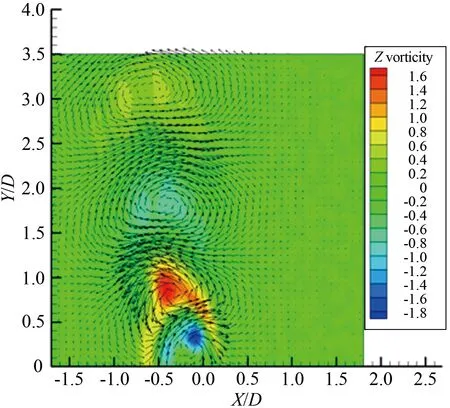
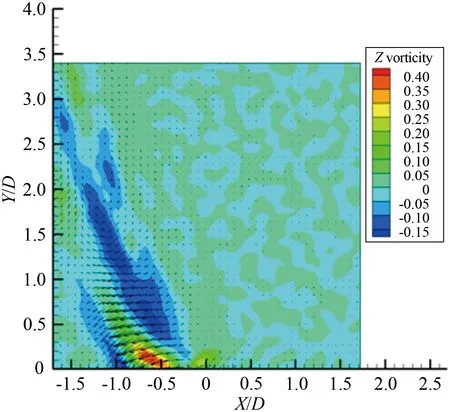
综上所述,圆柱旋转会明显改变圆柱的尾流场特征,随着旋转速度比变化,涡旋运动形态以及涡旋脱落频率都发生明显的改变。对于雷诺数Re≤200的层流流动进行数值模拟[4,12]发现,在旋转速度比0≤α≤1.90时存在交替的周期性涡旋脱落,在α≥4.23出现单侧的涡旋脱落。 对于雷诺数处于103 1.1 实验装置 实验是在中低速循环水槽中进行的,水槽主体由有机玻璃制成,包括稳定段、收缩段、实验段、扩散段和回流段。水槽工作段的尺寸为2 500mm×600mm×500mm(长×高×宽)。水槽的来流湍流度低于0.8%。圆柱的材料为有机玻璃,直径为25mm。圆柱由可调速的直流电机驱动,可以在0~12r/s转速范围内转动。实验使用德国Lavison公司2D2C-PIV来获得旋转圆柱尾迹的速度矢量场,实验装置如图1(a)所示。实验中使用的示踪粒子为聚苯乙烯颗粒,直径为10μm。 实验布置示意图如图1(b)所示,二维片光从水槽侧面照射圆柱下游流场,片光厚度为1mm,示踪粒子发出散射光,将CCD相机布置在水槽底部,对尾迹流场进行粒子图像的拍摄和记录。 (a) Picture of experimental apparatus (b) Schematic of experimental apparatus图1 实验装置图Fig.1 Experimental apparatus 1.2 参数设置 对于旋转圆柱,影响流动的2个重要参数是雷诺数Re=ρU∞D/μ(其中为U∞来流速度,D为探头直径,μ为流体动力粘性系数,ρ为流体密度)和旋转速度比α=ωr/U∞(其中ω为探头旋转角速度,r为探头半径)。根据雷诺数定义,为满足Re=1000,水槽的工作流速为0.04m/s。速度比分别为α=0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5和5.0。PIV系统激光能量设为最大值100mJ,相机的工作模式为双帧双曝光,采样频率为50Hz。每个工况流场图像拍摄样本数为2 500对,拍摄的相邻2对图片的时间间隔是1 000μs。相机分辨率2 048pixel×2 048pixel,拍摄流场尺寸为100mm×100mm。在进行互相关运算获得速度场时,问询域大小设为32pixel×32pixel,重叠率为50%。 1.3 POD技术 林昏晓冷笑一声后又问道:“那大小姐,你割哪儿呢?别以为在手指头上划破一点皮,就叫自杀。我告诉你,想死,就得……” POD是Lumley引入湍流研究的一种用于辨识大尺度湍流涡结构的数据处理方法。在POD方法中相干结构定义为空间变量的函数,从而使该函数具有最大的能量,即相干结构为本征函数φ(x)的线性组合,从而使 具有最大值。如果φ(x)使式(1)具有最大值,就意味着将流场投影到φ(x)上的平均能量比将流场投影到其他结构上的更大。在正交空间中,重复上述过程可以获得L2空间上φ(x)的完备集。POD法具有流场在本征函数上分解收敛快的优点。通过变量演化可知式(1)具有最大值的条件是φ(x)满足Fre-dholm积分方程的解,即 式中:δnm为Dirac函数。 通过前K阶主要含能本征函数的重构来描述随机速度场的一个低维模型,然而,基于PIV实验数据进行POD分析时样本的数量通常比空间网格点少很多。因此,矩阵R(x,x′)解的数量不比样本的数量多,这就极大地减少了工作量,这种POD方法称之为Snapshot POD方法[10-11]。 2.1 旋转圆柱绕流的瞬态流场 不同转速比工况下,瞬态流场的矢量场和涡强场分布如图2所示。其中,横坐标为展向方向,纵坐标为流向方向,运用圆柱直径对坐标进行无量纲,下文的表示均与此处相同。通过瞬时流场的分布可以看出,如图2(a)所示,当圆柱静止时圆柱两侧有明显的交替涡旋脱落,沿流向大约距离圆柱后驻点2倍直径距离上,涡量从剪切层区分离出来注入大尺度的涡旋中[6]。在图2(b)~(f)中,随着圆柱旋转速度逐渐变大,圆柱尾流瞬态流场发生了明显的变化:圆柱两侧的剪切层区逐渐变短,使涡量更早地注入到涡旋运动中,甚至当旋转速度比为α=5.0时,较高涡量剪切层区在流场的观测区中消失了,且圆柱的旋转使较高涡量区偏向了一侧。当圆柱开始旋转时,大尺度涡旋形成所需的距离逐渐变短,圆柱绕流的尾迹在流向上的尺度变小。 (a) α=0 (b) α=1.0 (c) α=1.5 (d) α=2.0 (e) α=3.0 (f) α=5.0 2.2 流场的频率特性 在圆柱绕流问题中,大尺度涡旋运动是重要的流场特征,而且涡旋运动具有一定的周期性,涡旋的频率值是尾流场的重要参数。为了分析流场的频率特性,在尾迹大尺度涡旋区中,选择一数据采样点,采样点的位置在图2中给出,对该点展向速度Vx随时间变化的序列进行傅里叶分析,以探讨流场的频率特性。如图3和4所示,能谱图横轴代表的是频率,纵轴代表的是能量分布。在图3(a)中,当圆柱静止即旋转速度比α=0时,频率值f=0.34Hz所对应的能谱值最大,该点的频率值可以认为是该点速度分量Vx频率[13]。根据斯托罗哈尔数定义 式中:f是涡旋脱落的频率,U∞是来流速度,d为圆柱直径。当250 根据经验公式,本实验条件下静止圆柱尾迹中涡旋的脱落频率fc≈0.31Hz。虽然实验测量值与计算值之间有近10%的误差,但是采样点速度分量的频率依然可以用来表征圆柱尾流中涡旋的脱落频率。 (a) Spectrum profile with 0≤α≤2.0 (b) Changing law of frequency with 0≤α≤2.0 Fig.3 Spectra with various rotating speed ratios and the change of frequency with rotating speed ratio(0≤α≤2.0) 如图3(a)所示,在这4个不同工况频谱中也都存在一个主要频率,这个主频对应着涡旋脱落的频率。图3(b)是主要频率随旋转速度比的变化曲线,可明显看出随着转速比的增大,涡旋频率有逐渐增大的趋势,这与CHEW等人的数值模拟结果相同[3]。这时在充分发展的尾迹区主要的频率还是涡旋脱落的频率,流场的主要结构也还是周期性的涡旋脱落。图4(a)旋转速度比由2增加到5,在图中依然存在能谱值最大点,但是与其他频率的能谱值相差不多,也就是这时的采样点的速度分量变化并无明显的主要频率,这时速度场不具有明显的周期性,圆柱尾迹中涡旋周期性的脱落受到抑制。在图4(a)中依然存在能谱值最大点,但是伴随着其它频率的出现,从频谱分布上很难区分出主要的涡旋脱落频率,这说明随着圆柱旋转速度的增加,特别是转速比大于2.5以后,旋转圆柱尾迹的尾迹区域中已经很难捕获其脱落特性,流场更多是受到了旋转圆柱的线速度的影响,脱落特性已经不再是主要特征。同时,也表明了流场更多的是趋向于一种相对更均匀的流场分布,这也与瞬时流场中随着旋转速度比增大,涡量的强度和尺度都变小的结果一致。由图4(b)旋转速度比与频率曲线可知,当旋转速度比大于3.5时,频谱最大值位于低频区域,表明这时流场中出现的主要特征是低频的非周期性波动。 (a) Spectrum profile with 2.5≤α≤5.0 (b) Changing law of frequency with 2.5≤α≤5.0 Fig.4 Spectra with various rotating speed ratios and the change of frequency with rotating speed ratio(2.5≤α≤5.0) 2.3 POD 模态分解 对获得速度场序列进行正交模态分解。通过正交模态分解可以获得流场的主要能量结构,以及各个模态所对应的能量比例[14]。图5(a)~(k)是不同转速比下POD分解获得流场的第一模态的信息。由图5可知,静止的圆柱尾流第一模态与旋转圆柱的尾流明显不同。在旋转速度比0.5≤α≤2.5时,第一模态有明显的沿流向分布的类似“涡旋”的结构。随着转速比的增大,这些结构有2个明显的变化趋势:一是随着转速比增大,第一模态中大尺度结构逐渐向流体被减速的一侧偏转;二是随着转速比增大,整个结构靠近圆柱,表明能量随着转速比的升高,含能高的结构出现在了更靠近圆柱的下游区域。当旋转速度比α≥3.0时,第一模态形态发生剧烈的变化,沿流向分布的类涡旋结构完全消失。当转速比在3.0≤α≤5.0范围内时,第一模态的结构是向流体被减速一侧倾斜的强剪切带状区域,对应在频谱分析中低频的结构。在高速带内,矢量方向大致相同。这一结构表明在较高旋转速度比圆柱旋转对流场起主要作用,流场更多是受到了旋转圆柱的线速度的影响,圆柱周围出现了强剪切层状的结构。 由于旋转圆柱绕流尾流场较静止圆柱绕流问题要复杂许多,旋转圆柱绕流流场特征是绕流的涡旋运动与圆柱旋转共同作用的结果。为了更好分析流场的特征,进行POD分析时流场的第二模态也被提取出来,如图6所示,为流场的第二模态。 同样地在旋转速度比0.5≤α≤2.5时,流场的第二模态有明显的沿流向分布的类似“涡旋”结构,但是形态与第一模态明显不同。当旋转速度比α=3.0时,第一模态中的结构表现出由高速旋转产生的剪切流动的特征,而流场第二模态具有明显的涡旋结构特征,但是比0.5≤α≤2.5尺度要小,并且“涡量值”也要小。说明旋转速度比为3.0时,流场中存在2种不同结构的相互作用。当旋转速度比超过3.0后,流场的第二模态同样也是由高速旋转产生剪切流动的特征,但其形态与第一模态不同。当旋转速度比在0≤α≤3.0范围内时,流场的第一模态和第二模态中存在涡旋结构,说明这时流场中一直存在着涡旋脱落运动。但是涡旋运动相比旋转作用逐渐减弱,3.0是临界点,在转速比为3.0时,第一模态中没有大尺度涡旋结构,第二模态才有。当旋转速度比大于3.0时,流场中第一模态与第二模态中的涡旋结构都不存在了。同样这一现象与文献[3]中的结论相吻合。另外,在旋转速度比大于4.23时,没有发现层流旋转圆柱扰流的数值模拟中存在单侧涡旋脱落。 (a) α=0 (b) α=0.5 (c) α=1.0 (d) α=1.5 (e) α=2.0 (f) α=2.5 (g) α=3.0 (h) α=3.5 (i) α=4.0 (j) α=4.5 (k) α=5.0 POD不仅可以获得流场的模态信息,还可以得到流场模态的能量分布[15]。图7就是所有转速比下流场前十个模态的能量信息。从图7中可以看出,在转速比0≤α≤2.0时,第一和第二模态的能量比例都在15%以上,当转速比超出这个范围时,第一和第二模态的能量比例都在15%以下,在第六模态以后它们的能量分布大致相同。由此可知圆柱的旋转改变流场中各个模态中能量分布,当转速比大于2.0时,圆柱旋转使低模态的能量比例减小。在POD方法中,较低的模态具有较高的能量对应的是较大尺度的结构,较高的模态具有较小的能量对应的是小尺度的结构,所以旋转改变了流场的空间尺度分布。当转速比超过2.0时,圆柱的旋转使流场的空间尺度变小。这是由于圆柱的高速旋转增加流场的不稳定性,加剧涡旋之间的相互作用,使尾流场中的大尺度涡旋结构变成小尺度的涡旋结构,从而使流场主要结构的尺度变小。 (a) α=0 (b) α=0.5 (c) α=1.0 (d) α=1.5 (e) α=2.0 (f) α=2.5 (g) α=3.0 (h) α=3.5 (i) α=4.0 (j) α=4.5 (k) α=5.0 图7 不同旋转速度比前十模态的能量分布 Fig.7 Energy distribution of first ten modes with various rotating speed ratios 本实验采用PIV技术对雷诺数Re=1 000圆柱旋转速度比为0~5.0的旋转圆柱绕流进行研究。通过对实验结果的研究得出以下结论: (1)圆柱的旋转改变了流场的频率特性,在0≤α≤2.0时,随着转速比增大,涡旋脱落频率逐渐增大。当转速比大于2.0时流场的周期性逐渐减弱,当转速比大于3.5时流场表现出低频的波动。 (2)圆柱的旋转改变了涡旋脱落的形式,随着转速比增大涡旋脱落被提前,圆柱尾迹长度变短。在0≤α≤2.5时流场中涡旋脱落起主要作用,当转速比大于3.0时圆柱的旋转起主要作用。 (3)圆柱的旋转使流场的能量重新分布,当转速比大于2.0时,流场主要模态的能量比例变小,流场的尺度变小。 对于投弃式海流剖面仪探头,周围的流场对探头的运动产生剧烈的影响,直接影响探头性能。通过对实验结果分析获得不同速度比圆柱尾流场特征的变化规律,为探头选择适当的工作参数提供理论依据。 [1] 刘宁, 何鸿鲲. 投弃式海流剖面测量仪测量原理研究[J]. 海洋技术, 2010, 29(1): 8-11. Liu Ning, He Hongkun. Study on the theory of expendable current profiler measurement[J]. Ocean Technology, 2010, 29(1): 8-11. [2] 陈文义, 张瑞, 刘宁, 等. 投弃式海流剖面仪探头流场数值模拟[J]. 科技导报, 2010, 28(20): 62-65. Chen Wenyi, Zhang Rui, Liu Ning. et al. Numerical simulation the flow field of expendable current profiler probe[J]. Science & Technology Review, 2010, 28(20): 62-65. [3] Chew Y T, Cheng M, Luo S C. A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme[J]. Journal of Fluid Mechanics, 1995, 299: 35-71. [4] Mittal S, Kumar B. Flow past a rotating cylinder[J]. Journal of Fluid Mechanics, 2003, 476: 303-334. [5] Dol S S, Kopp G A, Martinuzzi R J. The suppression of periodic vortex shedding from a rotating circular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6): 1164-1184. [6] Lam K M. Vortex shedding flow behind a slowly rotating circular cylinder[J]. Journal of Fluids and Structures, 2009, 25(2): 245-262. [7] Lee S J, Lee J Y. PIV measurements of the wake behind a rotationally oscillating circular cylinder[J]. Journal of Fluids and Structures, 2008, 24(1): 2-17. [8] Lam K M, Dai G Q. Formation of vortex street and vortex pair from a circular cylinder oscillating in water[J]. Experimental Thermal and Fluid Science, 2002, 26(8): 901-915. [9] 蒋贵丰, 栗晶, 吴丹, 等. 气固两相圆湍撞击流的POD结构分析[J]. 工程热物理学报, 2013, 34(6): 1101-1104. Jiang Guifeng, Li Jing, Wu Dan, et al. Analysis of turbulent coherent structures in round particle-laden opposed jets based on pod method[J]. Journal of Engineering Thermo Physics, 2013, 34(6): 1101-1104. [10] 蔡伟华, 李凤臣, 张红娜, 等. 减阻水溶液槽道湍流特性POD分析[J]. 哈尔滨工业大学学报, 2012, 44(7): 51-57. Cai Weihua, Li Fengchen, Zhang Hongna, et al. POD analysis for the turbulent characteristics of channel flow with drag-reducing aqueous solution [J]. Journal of Harbin Institute of Technology, 2012, 44(7): 51-57. [11] Gurka R, Liberzon A, Hetsroni G. POD of vorticity fields: A method for spatial characterization of coherent structures[J]. International Journal of Heat and Fluid Flow, 2006, 27(3): 416-423. [12] Liné A, Gabelle J C, Morchain J, et al. On POD analysis of PIV measurements applied to mixing in a stirred vessel with a shear thinning fluid[J]. Chemical Engineering Research and Design, 2013, 91(11): 2073-2083. [13] Berkooz G, Holmes P, Lumley J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539-575. [14] Stojkovic D, Schon P, Breuer M, et al. On the new vortex shedding mode past a rotating circular cylinder[J]. Physics of Fluids, 2003, 15(5): 1257-1260. [15] Guo X, Lin J, Tu C, et al. Flow past two rotating circular cylinders in a side-by-side arrangement[J]. Journal of Hydrodynamics, 2009, 21(2): 143-151. [16] 桑文慧, 孙志强, 周孑民. 有限流道内低雷诺数二维圆柱绕流数值模拟[J]. 中南大学学报(自然科学版), 2012, 43(3): 1166- 1170. Sang Wenhui, Sun Zhiqiang, Zhou Jiemin. Numerical simulation of two-dimensional flow around a circular cylinder at low Reynolds Numbers in finite channel[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 1166- 1170. (编辑:杨 娟) Experimental study on the flow past a rotating cylinder with PIV Sun Jiao1,2,3, Zhang Bin1,2, Tang Zhanqi2,4, Chen Wenyi1,2,* (1. Department of Process Equipment and Control Engineering,Hebei University of Technology, Tianjin 300130, China; 2. Research Center of Engineering Fluid and Process Enhancement, Hebei University of Technology, Tianjin 300130, China; 3. Department of Mechanics, Tianjin University, Tianjin 300072, China; 4. Dempartment of Mechanics Engineering, Hebei University of Technology, Tianjin 300130, China) Flow field behind the expendable current profiler(XCP) is a typical flow past rotating cylinder. Flow field around a cylinder is crucial to the probe motion state which would affect the performance of the probe singnificantly. So it is necessary to investigate the flow field around the rotating cylinder using experimental methods. For the flow past a rotating cylinder, there are two important factors affecting the flow pattern of the rotating cylinder, namely the Reynolds number and the speed ratio. With constant Reynolds number(Re=1 000) and different speed ratios, defined as the ratio of cylindrical rotating speed to stream velocity, the experiment was conducted in a circulated water channel, and the wake flow fields under different speed ratios were acquired by PIV. To analyze the rotating cylinder wake structure variation caused by rotation, the transient flow fields of different speed ratios at any time were chosen. In order to obtain the frequency information of the flow field, energy spectrum analysis was carried out on the flow field to extract vortex shedding frequency. Proper otrhogonal decomposition (POD) was used to extract large scale structure and energy contained in large structure which varied with the increase of speed ratio. It was found that the rotating cylinder changed the wake structure and made the wake scale smaller. As the speed ratio increased, there were two different transformation trends of cylinder flow wake. When speed ratio varied between 0 and 2.0, periodic vortex shedding was observed clearly. The periodicity of the flow field was the main character according to the relationship of spectrum and frequency. With the increase of the speed ratio, vortex shedding frequency had a rising trend. However, when the speed ratio varied between 2.0 and 5.0, the periodicity of the flow field became weak; flow field adopted a low frequency and high shear pattern. Furthermore, as the speed ratio increased, the vortex scale became smaller. At a higher rotational speed ratio, the flow field energy was redistributed. rotating cylinder;speed ratio;vortex shedding frequency;vortex scale;proper orthogonal decomposition;PIV measurement 1672-9897(2016)01-0081-10 10.11729/syltlx20150037 2015-03-09; 2015-10-21 国家自然科学基金(11572357, 11502066);国家高技术研究发展计划(863) (2006AA09A304);河北省自然科学基金(D2009000035) SunJ,ZhangB,TangZQ,etal.ExperimentalstudyonflowpastarotatingcylinderwithPIV.JournalofExperimentsinFluidMechanics, 2016, 30(1): 81-90. 孙姣, 张宾, 唐湛棋, 等. 旋转圆柱绕流的PIV实验研究. 实验流体力学, 2016, 30(1): 81-90. O357.5+2 A 孙 姣(1978-),女,河北辛集人,讲师,博士后。研究方向:实验流体力学。通信地址:天津市红桥区光荣道8号河北工业大学东院300#信箱(300130)。E-mail:sunjiao2007@163.com *通信作者 E-mail: cwy63@126.com1 实验装置及方法



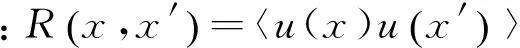
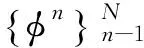
2 结果及分析





















3 结 论

