最优冲突回避码的具体构造

黄必昌，朱文兴

(1. 百色学院数学与统计学院，广西 百色　533000； 2. 福州大学离散数学与理论计算机科学研究中心，福建 福州　350002)

最优冲突回避码的具体构造

黄必昌1, 2，朱文兴2

(1. 百色学院数学与统计学院，广西 百色533000； 2. 福州大学离散数学与理论计算机科学研究中心，福建 福州350002)

摘要：冲突回避码被应用于多分址冲突信道中，目前对最优冲突回避码的具体构造取得的结果大多是码重k=3, 4, 5, 6, 7的情况，对码重k>7具体构造结果比较少. 为此，利用已有的构造方法结合数论相关知识，进一步构造码重k=8, 9, 10, 11, 12，码长n=(k-1)p时的最优冲突回避码新结果.

关键词：冲突回避码； 码重； 二次剩余； 分圆类

0引言

冲突回避码(conflict-avoiding code, CAC)作为协议序列被应用于无反馈多分址信道(冲突信道)[1-2]，多分址信道模型可参看文献[1]. 下面给出冲突回避码的数学描述.

Δ(A)={x-y(modn):x, y∈A, x≠y}

设C是Zn一些k阶子集A⊆Zn的集合，则C被称为长度为n重量为k的冲突回避码, 若其满足:

Δ(A1)∩Δ(A2)=φ, ∀A1, A2∈C, A1≠A2

每个元素A∈C称为一个码字. 对于给定的n和k，符号CAC(n, k)表示所有长度为n重量为k的冲突回避码. 当光正交码互相关性等于1时可看做一种冲突回避码，关于光正交码的定义可参看文献[3].

为了寻求最优码，人们主要考虑一种特殊的码——等差码. 主要原因是这类码的码字差集不同元素的个数比较少，相应地会得到较多的码字.

对于冲突回避码C∈CAC(n, k)，码字数量是保证潜在用户数量传输数据的有效性和可靠性. 最优冲突回避码能保证最大数量的潜在用户有效可靠地传输信息. 码字的重量k(汉明码重量)表示用户在每个时段的n个时槽里发送k个数据包[4].

1相关构造及证明

为了方便理解，先介绍一些常用的概念和符号.

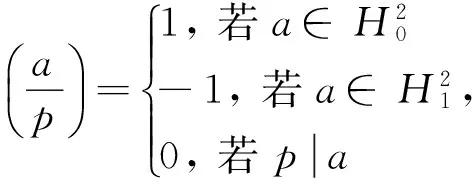
关于勒让德符号，当a=-1, 2, 3, 5, 7时有如下结果，为叙述方便记作引理1.

引理 1[12]若p是奇素数，则

引理2[4]设e≥1和s>1都是整数，p=2em+1是素数且使得每一个(i-es, i-(e-1)s, …, i+(e-1)s), 1≤i≤s-1和(±s, ±2s, …, ±es)都各自形成一个2e阶分圆类代表系. 那么存在一个码C∈CACe(sp, k=es+1)包含m个码字，且满足ZspΔ(C)=pZsp.

引理3[11]若m>s，则引理2构造的码C∈CACe(sp, k=es+1)是最优的.

下面，用引理1和引理2来具体构造等差码.

定理1若p=2m+1是素数且p≡71, 119(mod120)，则存在码C∈CACe(7p, 8)包含m个码字.

而当p≡71, 119(mod120)时以上条件满足. 从而命题得证.

证明由定理1，每个pi=2mi+1, 1≤i≤r都是使得Ci∈CACe(7pi, 8)存在的素数，则反复利用引理4递推构造即可.

定理2若p=2m+1是素数且p≡71, 191, 239, 359, 431, 599(mod840)，则存在码C∈CACe(8p, 9)包含m个码字.

而当p≡71, 191, 239, 359, 431, 599(mod840)时以上条件满足. 从而命题得证.

证明根据定理2，每个pi=2mi+1, 1≤i≤r都是使得Ci∈CACe(8pi, 9)存在的素数，则反复利用引理4递推构造即可.

定理3若p=2m+1是素数且p≡39, 71, 79, 151, 191, 239(mod280)，则存在码C∈CACe(9p, 10)包含m个码字.

证明由定理3，每个pi=2mi+1, 1≤i≤r都是使得Ci∈CACe(7pi, 8)存在的素数，则反复利用引理4递推构造即可.

定理4若p=2m+1是素数且p≡23, 55, 71, 95(mod168)，则存在码C∈CACe(10p, 11)包含m个码字.

证明由定理4，每个pi=2mi+1, 1≤i≤r都是使得Ci∈CACe(10pi, 11)存在的素数，反复利用引理4递推构造即可.

定理5若p=2m+1是素数且p≡71, 191, 239, 359, 431, 599(mod840)，则存在码C∈CACe(11p, 12)包含m个码字.

证明由定理5，每个pi=2mi+1, 1≤i≤r都是使得Ci∈CACe(11pi, 12)存在的素数，反复利用引理4递推构造即可.

2结论

参考文献：

[1] MASSEY J L, MATHYS P. The collision channel without feedback[J]. IEEE Transactions on Information Theory, 1985, 31(2): 192-204.

[2] GRYORFI N Q A L, MASSEY J L. Constructions of binary constant weight cyclic codes and cyclically permutable codes[J]. IEEE Transactions on Information Theory, 1992, 38(3): 940-949.

[3] SALEHI J A. Code division multiple-access techniques in optical fiber networks: I. fundamental principles[J]. IEEE Transactions on Communications, 1989, 37(8): 824-833.

[4] MOMIHARA K, MULLER M, SATOH J,etal. Constant weight conflict avoiding codes[J]. Siam Journal on Discrete Mathematics, 2008, 21(4): 959-979.

[5] FU H L, LI Y H, MISHIMA M. Optimal conflict avoiding codes of even length and weight 3[J]. IEEE Transactions on Information Theory, 2011, 57(8): 5 572-5 572.

[6] JIMBO M, MISHIMA M, JANISZEWSKI S,etal. On conflict avoiding codes of lengthn=4mfor three active users[J]. IEEE Transactions on Information Theory, 2007, 53(8): 2 732-2 742.

[7] LEVENSHTEIN V I. Conflict-avoiding codes for three active users and cyclic triple systems[J]. Problems of Information Transmission, 2007, 43(3): 199-212.

[8] MISHIMA M, FU H L, URUNO S. Optimal conflict avoiding codes of lengthn=(0 mod16) and weight 3[J]. Designs, Codes and Cryptography, 2009, 52(3): 275-291.

[9] Momihara K. Necessary and sufficient conditions for tight equidifference conflict avoiding codes of weight three[J]. Designs, Codes and Cryptography, 2007, 45(3): 379-390.

[10] MA W P, ZHAO C E, SHEN D S. New optimal constructions of conflict-avoiding codes of odd length and weight 3[J]. Designs, Codes and Cryptography, 2014, 73(3): 791-804.

[11] SHUM K W, WONG W S, CHEN C S. A general upper bound on the size of constant weight conflict avoiding codes[J]. IEEE Transactions on Information Theory, 2010, 56(7): 3 265-3 276.

[12] NATHANSON M B. Elementary methods in number theory[M]. New York: Springer-Verlag, 2000.

(责任编辑： 郑美莺)

Explicit constructions of optimal conflict-avoiding codes

HUANG Bichang1, 2, ZHU Wenxing2

(1. College of Mathematics and Statistics, Baise University, Baise, Guangxi 533000, China；2. Center for Discrete Mathematics and Theoretical Computer Science, Fuzhou University, Fuzhou, Fujian 350002, China)

Abstract:Conflict-avoiding code was applied in multiple-access in the collision channel. Previously, researchers investigate explicit constructions of optimal conflict-avoiding code in the case of k=3, 4, 5, 6, 7. And there is very few results in the case of k>7. In this paper, combing pre-existing constructions with the related knowledge of number theory, a new infinite classes of optimal conflict-avoiding codes with weight k=8, 9, 10, 11, 12 and length n=(k-1)p are obtained.

Keywords:conflict-avoiding code； code weight； quadratic residue； cyclotomic class

DOI:10.7631/issn.1000-2243.2016.03.0390

文章编号：1000-2243(2016)03-0390-04

收稿日期:2015-12-01

通讯作者:朱文兴(1968-)，教授，主要从事优化理论与算法研究，wxzhu@fzu.edu.cn

基金项目：国家自然科学基金资助项目(61170308)； 广西省自然科学基金资助项目(2013GXNSFAA019022)； 广西省高校科研项目(2013YB246)； 百色学院科研基金资助项目(2012KB01)

中图分类号：O157.4

文献标识码：A