基于多准则寻优策略的差分进化算法

陈　岩,王宗宪

(沈阳工业大学 理学院,辽宁 沈阳 110870)

基于多准则寻优策略的差分进化算法

陈岩,王宗宪

(沈阳工业大学 理学院,辽宁 沈阳 110870)

摘要：在差分进化算法的基础上,提出一种基于多准则寻优策略的改进差分进化算法。该算法可以动态调整变异因子和交叉概率,基于文中提出的多准则寻优策略,通过个体适应度、个体间距离等评价指标判断个体的优劣程度,并且可以降低种群的高密度程度,增强种群多样性。这种判断机制可以有效避免种群过早收敛,易陷入局部最优的风险。通过具体的测试函数对算法进行测试,并与标准差分进化算法进行比较,结果显示算法寻优效果较好,可以较快地得到全局最优解。

关键词：多准则寻优;差分进化算法;启发式算法;个体适应度

近年来,在实际应用中,人们对数值算法的要求越来越高,传统数值寻优方法虽然理论基础较好,能够给出解析解,但是对问题本身也有较为苛刻的要求,如需要函数的梯度、可导性等信息,并且随着问题规模的扩大,其计算复杂度也会呈指数形式增长。相较于传统优化方法,进化算法处理该类问题时,不需要函数具有过多的数学性质,并且具有计算速度快、解集可限定在某一误差范围之内等特点,因而得到广泛应用。

差分进化(differential evolution,DE)算法是Storn与Price[1]于20世纪90年代提出的一种进化算法。差分进化算法虽然是一种新兴算法,但是在数值计算领域反响很好,应用范围广泛,相关研究工作进展迅速。2004年谢晓锋等[2]对差分进化算法的缩放因子进行了讨论；2006年吴亮红等[3]提出自适应二次变异差分进化算法，Suganthan等[4]提出一种自适应差分进化算法,通过对上代种群的学习生产新的参数；2007年刘波等[5]对差分进化算法的发展作出了较全面地描述；2008年王培崇等[6]提出基于两种进化模式的协作差分进化算法，2009年Qin等[7]也提出一种自适应进化算法,王培崇等[8]对差分进化算法进行了系统分析,并对其发展进行了展望；2011年Swagatam等[9]对差分进化算法的研究现状进行了总结,Mallipeddi等[10]从变异角度对算法提出新见解；2012年Islam等[11]对差分进化算法的变异与交叉策略进行改进。差分进化算法虽然具有很多优异的特性,但是存在早熟、易陷入局部最优、收敛速度较慢、参数因子选取不方便等缺点。

差分进化算法的选择过程是根据解的适应度进行评价,若解的适应度较高则保留该解,否则放弃。这种选择机制可以筛选出当前解集中较好的部分,但也存在一定局限性：该过程并不能确保当前解集具有良好的多样性,易导致解集陷入局部最优。本研究通过对适应度值、个体间距离等信息综合考虑,提出一种可以动态调整参数的多准则寻优策略,该策略可以对群体中个体进行多方位的比较,从而更加准确地筛选出更具优势的个体。

1差分进化算法

差分进化算法是基于群体智能理论的优化算法,它通过种群内部个体间的互相合作与竞争,产生群体智能进行优化搜索。相较于其他进化算法,差分进化算法保留了基于种群的全局搜索策略,采用实数编码技术,利用基于差分的简单变异操作和一对一竞争生存策略,降低了进化操作的复杂性。该算法本质上是一种基于实数编码的具有保优策略的贪婪遗传算法,与遗传算法的进化思想相似,亦包含交叉、变异和选择的操作过程,二者的不同之处在于差分进化算法选择一对一的淘汰机制来更新当代种群,在不降低精确性的前提下降低操作复杂性。

标准差分进化算法的操作过程包含变异、交叉和选择三个步骤。初始解集在进化机制的作用下不断向最优方向游动,经过多次进化迭代之后,能达到可接受误差范围之内,给出可行解。该方法操作简单易行,求解速度较快。

标准差分进化算法流程如图1所示。

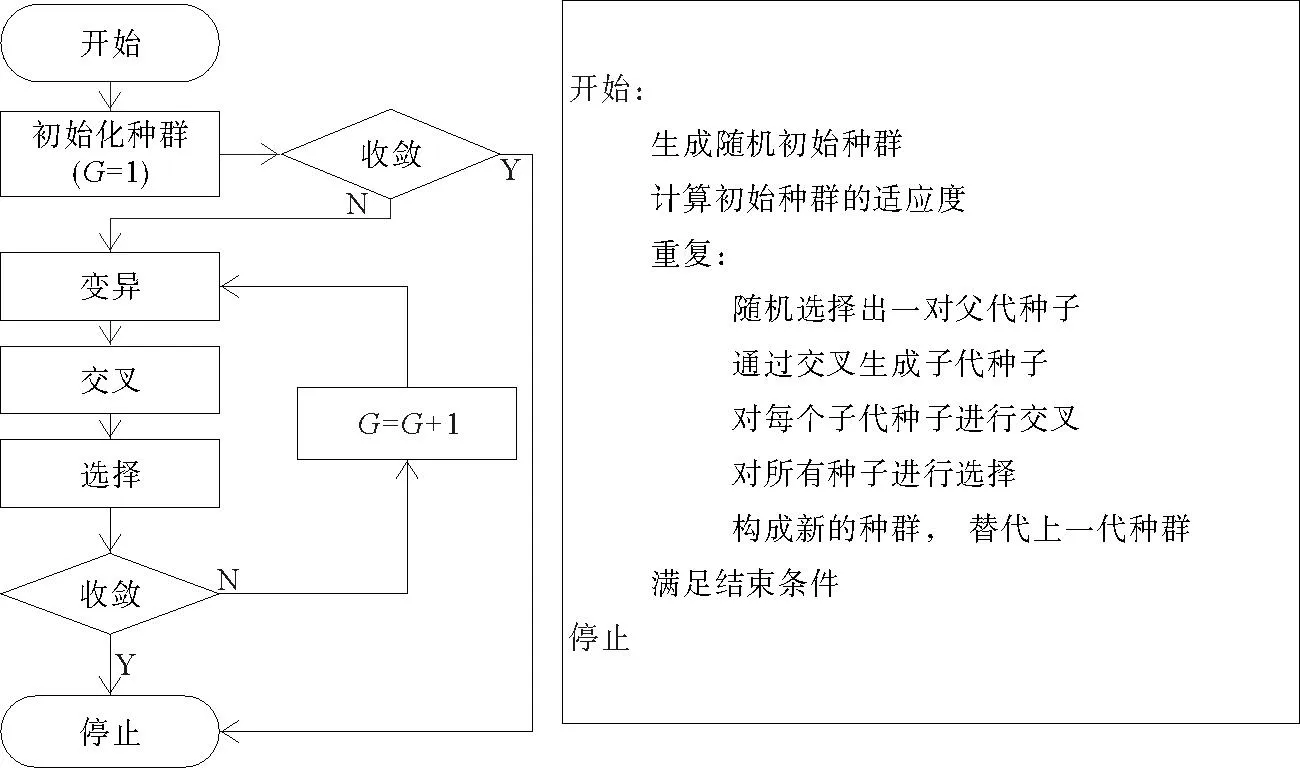
图1　差分进化算法流程图

利用差分进化算法求最值问题时,首先需要生成初始种群,该操作是在可行域内通过随机策略产生一个解集,即随机产生n个m维的个体,P=(X1，X2，…，XN),其中，Xi=(xi1，xi2，…，xim)T，i=1，2，…，N。结合进化思想,在初始解集的基础上进行变异、交叉、选择等进化操作。

1.1变异

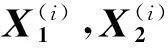
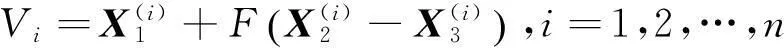
(1)

1.2交叉

交叉操作可以增强种群个体的多样性,该操作是将变异个体Vi与父代个体Xi进行交叉,从而产生新后代Ui的过程,如式(2)所示：

(2)

其中,Dj是一个随机数,且Dj～U(0，1)，jrand是[1,m]上的随机整数,Cr∈[0,1],称为交叉概率。

1.3选择

选择操作是利用贪婪准则对交叉后代与父代个体进行筛选的过程,其选择依据是个体适应度的优劣程度。适应度高的个体可以进入下一代种群,反之则被淘汰：

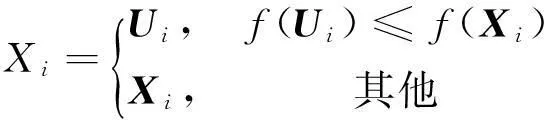
(3)

当可行解达到预设精度后停止迭代,并输出结果,也可以根据具体问题选定一个足够大的迭代次数,当达到该固定的迭代次数后,停止迭代,输出结果。

归纳起来,差分进化算法具有以下优点：

1)具有通用性,不要求问题具有很强的数学条件;

2)操作简单,易于实现;

3)群体效果明显,可以通过已知最优解进一步搜索;

4)易与其他方法混合使用。

2基于多准则寻优策略的差分进化算法

2.1种群生存规模

进化算法借鉴了生物进化过程中的相关概念与机制,并将其运用到数值计算或问题寻优过程当中。但生物在进化过程中以种群为单位,种群规模在生物进化中有着重要地位,这将涉及到种群生存能力分析(population viability analysis)理论。种群生存能力分析是生物学中研究如何保护生物避免灭绝的一个热点[12-14],主要研究随机干扰对小种群灭绝的影响,目的是确定最小生存种群(minimum viable population,MVP)数量,把种群灭绝的可能性减少到可接受水平。

最小生存种群数量指的是种群免遭灭绝而必须维持的最低个体数量，或是确保某一物种长期存活所必需的个体数。Franklin[15]曾提出小族群管理的50/500法则,指出为了防止族群在短期内出现近交衰退的情形,族群中至少需要50个个体,而需要500个以上的个体才能维持种群的遗传变异性。

本研究结合最小生存种群数量的概念与50/500法则,在差分进化算法中引入最小生存种群数量的概念,为进化算法的种群规模制定一个相对明确的取值范围,即在一般情况下种群规模应当不小于50,在计算机能力允许范围内,应当扩大种群规模至500个个体以上。

2.2变异因子与交叉概率

进化算法的搜索性能取决于算法全局探索和局部开发能力的平衡,这就需要对算法中的参数进行恰当的选取,差分进化算法中的变异因子与交叉概率的选取直接影响算法的收敛能力与计算速度。变异因子F一般情况下是人为选取的一个经验值,受人为因素影响较大。交叉概率Cr的选取过程亦如此。文献[16]对差分进化算法的变异因子与交叉概率的选取过程进行分析,提出变异因子F取值在[0.5,1]时算法效果较好,交叉概率Cr的选取则需要根据求解函数进行选取,一般单峰函数的值相对大一些,在[0.6,0.8],多峰函数Cr的值相对小一些,在[0.1,0.5]。根据文献[16]的研究成果,本研究引入动态适应调节机制,在参数选取过程中逐渐降低变异范围,以减弱解集在不断靠近最优解时产生的震荡现象,F取值变化示意图如图2所示。F为随机数,且F～U(a,b),本文中a取定值0.5。随着迭代次数的增加,b的取值随之不断减小,理论上每一代计算中b的值都可以减小,但是为了方便计算,本研究中令b每隔若干代变化一次,bi+1=bi-(b0-a)/(G/k),其中G为总的进化代数。k为间隔代数,也可以根据实际情况选取k的变化规则。令交叉概率Cr为一个随机数,且Cr～U(0,0.5)(可根据函数性质选取)。

图2　F变化示意图

2.3多准则寻优策略

本研究针对差分进化算法全局搜索能力较弱,收敛速度较差等问题,提出一种多准则寻优策略,该策略将结合群体的适应度、个体间距离等信息进行个体寻优,在一定程度上增强种群多样性及全局搜索能力。差分进化算法结合该策略对每一代种群进行筛选,将部分相似(冗余)个体或非优秀个体进行剔除,仅保留更具有代表性的个体或优势个体,在此过程中,为了使种群规模维持在一个相对稳定的状态,将对缺失部分进行重新填充,从而得到一个新的具有较强优势与丰富多样性的种群,如图3所示。

图3　种群中个体的筛选

定义1相似(冗余)个体是指两个体在解空间中距离较近,且其适应度排序值相近。

定义2非优秀个体是指在进化过程中,适应度较低的个体。

改进的差分进化算法计算过程中亦采取精英保留策略,对每一代种群中的优秀个体进行存档,并与下一代种群相融合以进行择优操作,利用这种机制可以使得每一代种群都能得到不劣于上一代的个体(解),并且该方式可以确保进化方向的正确性,保证优秀染色体更加有效地传递给下一代,避免进化“倒退”现象的发生。

该算法中需要对种群中的相似(冗余)个体进行处理,即剔除相似(冗余)个体以及非优秀个体。针对该问题需要考虑：①剔除哪些个体,其依据是什么；②种群中剔除多少个体比较合理，或种群中应保留多少个体比较合理。

问题①是要找到判断个体优劣程度的评价标准。在对种群中所有个体进行评价时,一般情况下是根据适应度指标找到优秀解,而本研究所提出的多准则寻优策略除了考虑个体的适应度之外,还考虑个体与个体间的距离,因为距离较近的个体可能处于同一递增或递减区间之内,此时会影响到种群多样性,而剔除个体的目的是为了剔除这些相似(冗余)个体或非优秀个体,因此除了以适应度作为评价依据外还应结合个体之间的距离进行评价,即采用两个评价依据：每个个体的适应度值；个体与个体之间的距离。

根据以上两个评价依据,首先按照适应度信息对所有个体进行排序,得到非优秀个体的相关信息,之后以该类别中适应度最高的个体为原点,计算该个体与其他个体间的距离(本文采用欧式距离),从而得到与该个体相似(冗余)个体的相关信息。

问题②是对种群中个体保留数量的讨论,此时需要考虑种群规模以及个体间的冗余度,本文给出每一代保留数量为Pop/10,其中Pop为种群规模。

对种群筛选完成之后,需要生成新的个体以补充因舍弃相似(冗余)个体或非优秀个体所产生的空缺。向种群中投放新个体时,此时仍采取一种互补策略,即尽量生成与现有个体差异性较大的个体,增强种群丰富度。

根据以上分析,该多准则寻优策略算法的步骤为：

Step 1计算种群中每个个体的适应度；

Step 2对当代种群中的个体按照适应度进行排序；

Step 3计算适应度最优个体与其他个体间的欧式距离；

Step 4根据距离的大小对每个个体进行编号；

Step 5结合权重,对适应度与个体间距离综合评价,并按优劣程度编号；

Step 6删除种群中相似(冗余)个体及非优秀个体；

Step 7生成新的个体,补充种群中的空缺位置。

3算例

选取8个较为常见的测试函数[17]进行数值实验,以验证上文所提出的改进差分进化算法的合理性以及可行性。

测试函数 1:Rosenbrock function

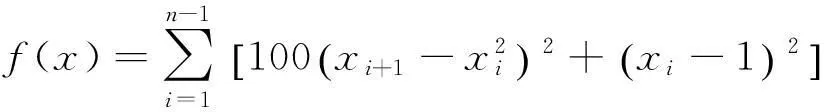
f(1,1)=0,-∞≤xi≤∞,1≤i≤n,此处n=2

(4)

测试函数 2:Beale function

f(3,0.5)=0,(-4.5≤x,y≤4.5)

(5)

测试函数 3:Goldstein-Price function

f(0,-1)=3,-2≤x,y≤2

(6)

测试函数 4:Matyas function

(7)

测试函数 5:Three-hump camel function

(8)

测试函数 6:Easom function

f(π,π)=-1,-100≤x,y≤100

(9)

测试函数 7:Ackley’s function

f(0,0)=0,-5≤x,y≤5

(10)

测试函数 8:Lévi function N.13

f(1,1)=0,-10≤x,y≤10

(11)

由于篇幅有限,仅给出测试函数7与测试函数8的函数图象,可以看出测试函数中存在无数多个极小点，能够很好地检测算法的全局寻优特性。每一个测试函数设定初始种群规模为200个,进化代数为100代,每个测试函数均计算20次,以平均值作为最终计算结果,该结果与真实解的对比关系如表1所示。

从表1中可以看出,本文提出的基于多准则寻优策略的改进差分进化算法在数值实验过程中表现出良好的特性,可以计算出测试函数的近似解,并且误差范围非常较小,满足精度需求。

为了进一步说明算法的有效性,给出标准差分进化算法与改进算法在求解过程中迭代次数与最优函数值的变化规律曲线,由于篇幅有限,仅给出Lévi N.13函数求解过程的对比曲线,如图6所示。

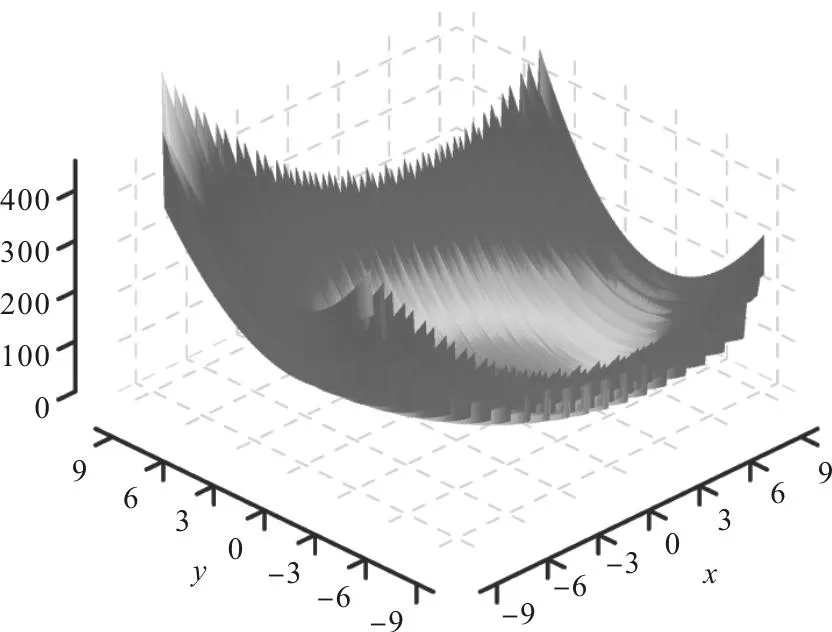
图4　测试函数7(Ackley’s function)

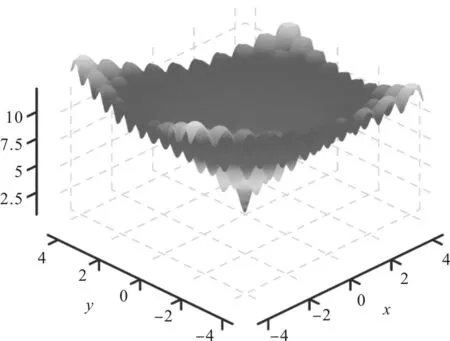
图5　测试函数8(Lévi function N.13)

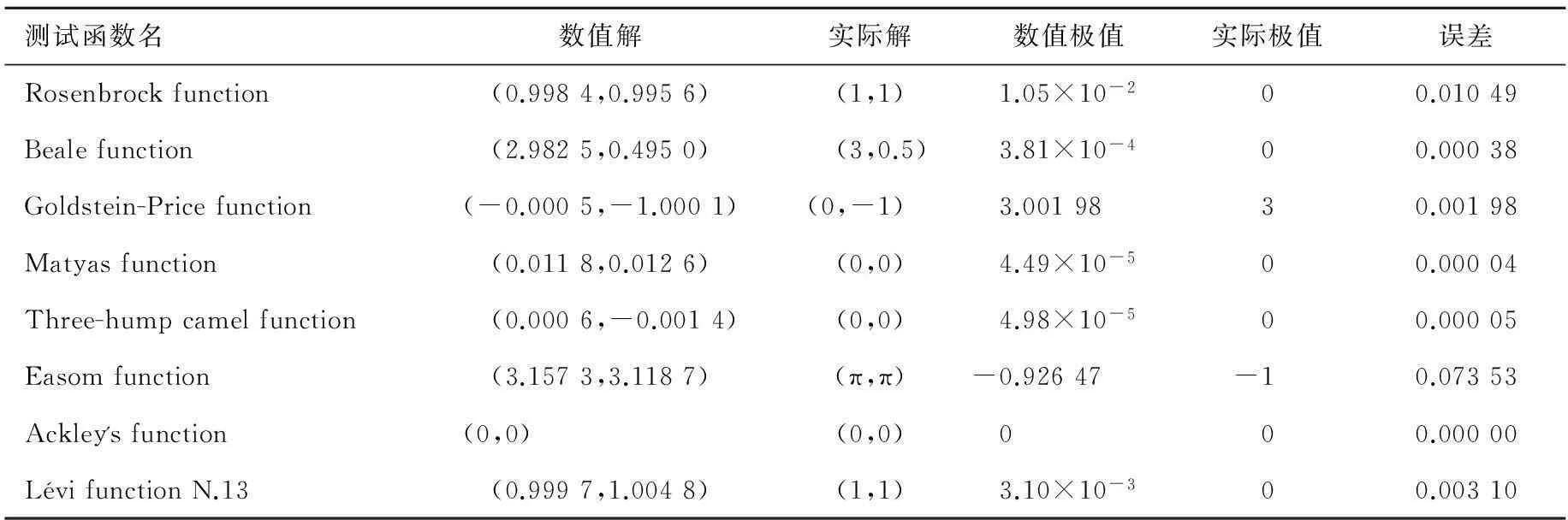
表1　测试函数对应的计算结果

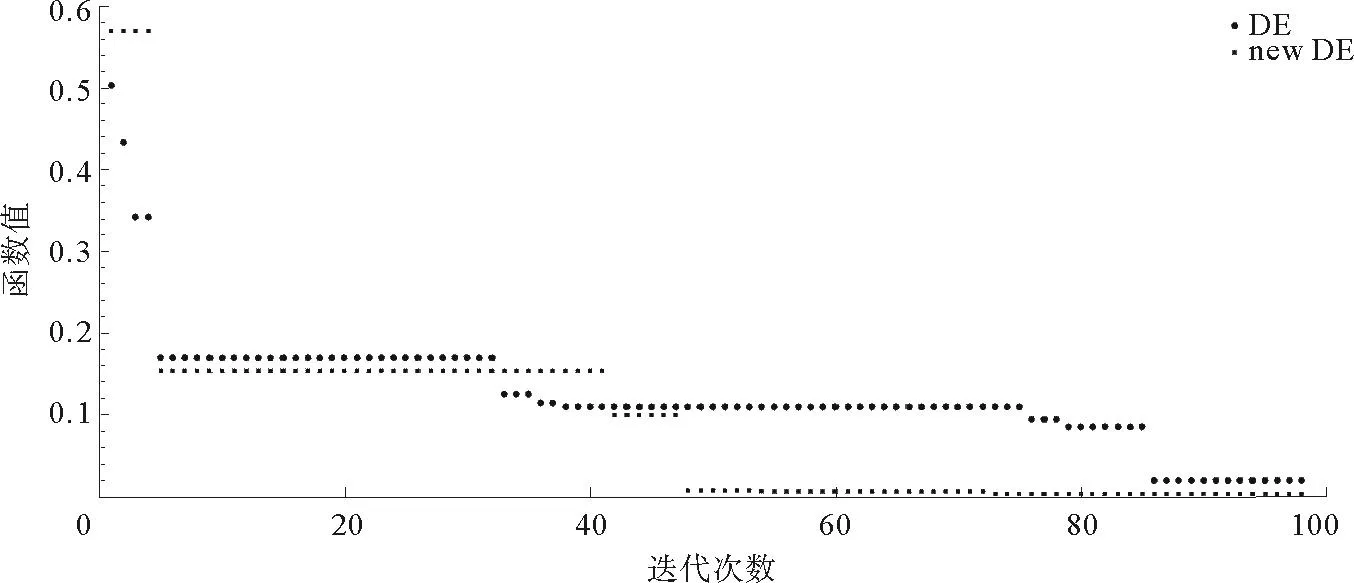
图6　两种算法求解Lévi N.13函数的对比关系

结合表1和图6可知,改进的差分进化算法的计算效果要优于传统的差分进化算法,并且可以更具有针对性地选择优势个体,使之得以保留,这不仅增强了种群多样性,也避免了搜索过程中易陷入局部极值的缺陷,大大增强了全局搜索能力。

4结束语

在经典差分进化算法基础上,提出一种动态调节机制用以选取变异因子;针对算法易陷入局部最优解,缺乏多样性的现象,提出一种多准则寻优策略,根据适应度与距离等属性综合评价解的优劣程度;通过排除冗余个体,加入互补解,增强解集多样性,避免陷入局部最优。最后，通过测试函数对算法进行测试。测试结果显示,改进差分进化算法具有可行性,并且收敛速度与计算精度上均表现良好。

参考文献：

[1]STORN R，PRICE K.Differential evolution：A simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997,11:341-359.

[2]谢晓锋,张文俊,张国瑞,等.差异演化的实验研究[J].控制与决策,2004,19(1):49-52.

XIE Xiaofeng,ZHANG Wenjun,ZHANG Guorui,et al.Empirical study of differential evolution[J].Control and Decision,2004,19(1):49-52.

[3]吴亮红,王耀南,袁小芳,等.自适应二次变异差分进化算法[J].控制与决策,2006,21(8):898-902.

WU Lianghong,WANG Yaonan,YUAN Xiaofang,et al.Differential evolution algorithm with adaptive second mutation[J].Control and Decision,2006,21(8):898-902.

[4]BREST J,GREINER S,BOSKOVIC B,et al.Self-adapting control parameters in differential evolution:A comparative study on numerical benchmark problems[J].Evolutionary Computation,IEEE Transactions on,2006,10(6):646-657.

[5]刘波,王凌,金以慧.差分进化算法研究进展[J].控制与决策,2007,22(7):721-729.

LIU Bo,WANG Ling,JIN Yihui.Advances in differential evolution[J].Control and Decision,2007,22(7):721-729.

[6]王培崇,贺毅朝,钱旭.基于两种进化模式的双种群协作差分演化算法[J].计算机工程与应用,2008,25:60-64.

WANG Peichong,HE Yichao,QIAN Xu.Cooperation differential evolution algorithm with double populations and two evolutionary models[J].Computer Engineering and Applications,2008,44(25):60-64.

[7]QIN A K,HUANG V L,SUGANTHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization[J].IEEE Transactions on Evolutionary Computation,2009,13(2):398-417.

[8]王培崇,钱旭,王月,等.差分进化计算研究综述[J].计算机工程与应用,2009,45(28):13-16.

WANG Peichong，QIAN Xu，WANG Yue，et al.Overview of differential evolution algorithm[J].Computer Engineering and Applications,2009,45(28):13-16.

[9]DAS S,SUGANTHAN P N.Differential evolution:A survey of the state-of-the-art[J].IEEE Transactions on Evolutionary Computation,2011,15(1):4-31.

[10]MALLIPEDDI R,SUGANTHAN P N,PAN Q K,et al.Differential evolution algorithm with ensemble of parameters and mutation strategies[J].Applied Soft Computing,2011,11(2):1679-1696.

[11]ISLAM S M,DAS S,GHOSH S,et al.An adaptive differential evolution algorithm with novel mutation and crossover stra-tegies for global numerical optimization[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(2):482-500.

[12]SHAFFER M L.Minimum population sizes for species conservation[J].Bioscience,1981,31:131-134.

[13]REED D H,O′GRADY J J,BROOK B W,et al.Estimates of minimum viable population sizes for vertebrates and factors influencing those estimates[J].Biological Conservation,2003,113(1):23-34.

[14]TRAILL L W,BRADSHAW C J A,BROOK B W.Minimum viable population size:A meta-analysis of 30 years of published estimates[J].Biological Conservation,2007,139(1):159-166.

[15]FRANKLIN I R.Evolutionary change in small populations[M]//Conservation Biology,An Evolutionary-Ecological Perspective.Sunderland,Massachusetts:Sinauer Associates,USA,1980:135-149.

[16]高岳林,刘军民.差分进化算法的参数研究[J].黑龙江大学自然科学学报,2009,26(1):81-85.

GAO Yuelin,LIU Junmin.Parameter study of differential evolution algorithm[J].Journal of Natural Science of Heilongjiang University,2009,26(1):81-85.

[17]Wikipedia contributors.Test functions for optimization[EB/OL].(2015-03-31)[2015-04-09]http://en.wikipedia.org/w/ index.php?title=Test—functions—for—optimization/&oldid=654396409.

(责任编辑：吕文红)

Differential Evolution Algorithm Based on Multi-criteria Optimization Strategy

CHEN Yan,WANG Zongxian

(College of Science,Shenyang University of Technology,Shenyang,Liaoning 110870,China)

Abstract:Based on differential evolution algorithm,this paper proposed an improved differential evolution algorithm with multi-criteria optimization strategy.This algorithm can adjust the mutation and crossover parameters dynamically,and evaluate individuals' grade of excellence with the evaluation indexes like individual fitness and distance between individuals on the basis of the proposed multi-criteria optimization strategies.It can also reduce the degree of population density and enhance population diversity.Although this evaluation mechanism can effectively avoid premature convergence of population,it tends to result in local optimum risk.After it was tested by some test functionsand compared with standard differential evolution algorithm,this improved algorithm was found to have the best optimization effect,being able to obtain the global optimal solution quickly.

Key words:multi-criteria optimization;differential evolution algorithm;heuristic algorithm;imdividual fitness

收稿日期：2015-11-19

作者简介：陈岩(1968—),男,辽宁沈阳人,教授,博士,主要从事优化方法和决策方面的研究. E-mail:crouse_chen@126.com

中图分类号：O221.4

文献标志码：A

文章编号：1672-3767(2016)01-0102-07