基于中美规范的高强钢筋混凝土梁受剪承载力对比分析

李　朋，郑鸿飞，张宪堂，刘　锋，王　飞，刘景伟，张永波

(1.山东科技大学 土木工程与建筑学院，山东 青岛 266590；2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；3.青岛市工程咨询院，山东 青岛 266071；4.青岛国家海洋科学研究中心，山东 青岛 266100)

基于中美规范的高强钢筋混凝土梁受剪承载力对比分析

李朋1，2，郑鸿飞1，2，张宪堂1,2，刘锋1，2，王飞1,2，刘景伟3，张永波4

(1.山东科技大学 土木工程与建筑学院，山东 青岛 266590；2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；3.青岛市工程咨询院，山东 青岛 266071；4.青岛国家海洋科学研究中心，山东 青岛 266100)

摘要：针对11根配置HRBF500高强钢筋的混凝土独立梁进行的受剪试验，分别采用我国《混凝土结构设计规范》(GB 50010-2010)和美国ACI 318-11规范公式计算构件的受剪承载力，并将公式计算值和试验实测值进行对比分析。研究结果表明，配置HRBF500高强钢筋混凝土梁，裂缝发展规律和受剪特征与配置普通钢筋混凝土梁基本相同，采用两国规范公式所得受剪承载力均小于实测值，有较大的安全余量，且两国规范受剪承载力的安全储备程度比较接近，承载力依据我国规范公式计算结果略大于依据美国规范公式所得计算值，相比美国规范，由混凝土项承担的受剪承载力，我国规范计算结果较大，而钢筋项承担受剪承载力略小。

关键词：高强钢筋；混凝土梁；中美规范；受剪承载力；对比分析

剪切是混凝土结构的一种基本受力状态。钢筋混凝土梁斜截面剪切破坏一直是国内外学者重点关注的研究课题，然而由于影响斜截面破坏的因素众多，像剪跨比、混凝土强度、箍筋配筋率、纵筋配筋率、斜截面上的骨料咬合力、截面尺寸和形状以及纵筋的销栓作用等，使得混凝土梁构件的剪切破坏机理复杂，至今仍是需要深入研究的课题[1-4]。各国设计规范关于混凝土梁结构受剪承载力的计算理论也不尽相同，目前已提出了多种计算理论，如桁架模型、变角桁架模型、压力场理论、压杆-拉杆理论等[5]。

HRBF500高强钢筋是采用控制钢筋轧制温度技术而研发的新型钢筋，具有强度高、延性好、成本低等特点。在结构中使用该高强钢筋可显著降低用钢量，同时结构用钢强度的提高，使得配筋量减少，可较好地改善混凝土结构中的“肥梁胖柱”现象并降低施工浇筑、振捣难度[6-9]，具有突出的社会效益和经济效益。

本研究基于11根配置HRBF500高强钢筋的混凝土独立梁在单向集中荷载作用下的受剪试验，对采用我国《混凝土结构设计规范》(GB 50010-2010)[10](以下简称“我国规范”)和美国ACI 318-11规范[11](以下简称“美国规范”)规定的受剪承载力计算公式的计算结果进行对比，并将公式计算值和试验实测值进行比较分析，以此来研究我国规范公式对配置高强钢筋的混凝土受剪构件计算的适用性，并为该高强钢筋在工程中的快速推广使用提供参考和科学依据。

1有腹筋构件受剪承载力计算理论

在我国规范中，配置腹筋的受弯构件斜截面承载力计算，是以剪压破坏形态为基础的，即构件发生剪切破坏时，与斜裂缝相交的箍筋和弯起的纵向钢筋屈服，受压区混凝土达到其强度发生破坏。图1为我国规范采用的计算模型，基于这一模型我国规范给出的配置箍筋的受弯构件受剪承载力一般表达式为：

Vu=Vcs+Vp+0.8fyAsbsinαs+0.8fpyApbsinαp。

(1)

其中：Vcs—构件混凝土和箍筋承担的剪力设计值；Vp—由预应力所提高的构件受剪承载力设计值；Asb，Apb—同一弯起平面内的非预应力弯起钢筋和预应力弯起钢筋的面积；αs，αp—斜截面上非预应力弯起钢筋、预应力弯起钢筋的切线与构件纵向轴线的夹角。

我国规范还规定，对于承受集中荷载为主的受弯构件集中荷载作用下(包括作用有多种荷载，(其中集中荷载对支座截面或节点边缘所产生的剪力值占总剪力的75%以上的情况)的独立梁)，混凝土和箍筋的受剪承载力按下式计算：

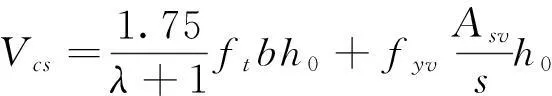
(2)

其中：λ—计算截面的剪跨比，可取为λ=a/h0,a为集中荷载作用点至支座或节点边缘的距离；当λ<1.5时，取λ=1.5，当λ>3时，取λ=3；集中荷载作用点至支座之间的箍筋为均匀配置。

图1　我国规范采用的受剪承载力计算模型

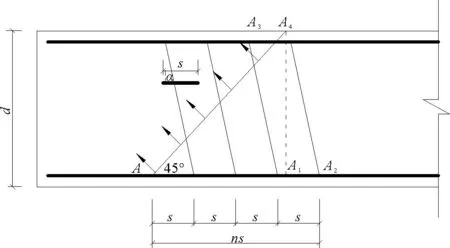
图2　美国规范采用的受剪承载力计算模型

对于我国规范规定的受剪承载力计算公式，混凝土承担的受剪承载力取试验结果的偏下限值，除考虑截面尺寸影响外，根据剪跨比的不同，分成斜压破坏、剪压破坏及斜拉破坏三种形态，这三种破坏形态与构件的剪跨比密切相关。混凝土抗拉强度取轴心抗拉设计值，箍筋承担的受剪承载力部分箍筋强度取抗拉强度设计值。我国规范4.2.3条规定，横向钢筋的抗拉强度设计值fyv按规范表4.2.3-1中的fy的数值采用；但用作受剪、受扭、受冲切承载力计算时，其数值大于360 N/mm2时应取360 N/mm2。

美国规范中没有“强度设计值”的概念，对每一种不同的受力状态，名义承载力乘以一个不同的承载力折减系数φ后得到设计承载力，同时美国规范认为对于同一种受力状态，钢筋强度和混凝土强度折减系数一致。美国规范对有腹筋受弯构件受剪承载力的计算是采用以修正的桁架模型为基础的简化计算方法，如图2所示。在桁架模型中，斜裂缝之间的混凝土小柱为压杆，与斜裂缝相交的钢筋为拉杆。美国规范的计算公式为：

Vu=φVn=φ(Vc+Vs)。

(3)

混凝土项承担的受剪承载力为：

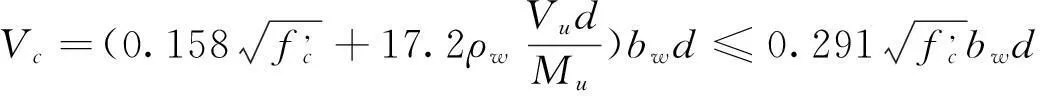
(4)

美国规范规定，对于大多数设计，为简便计算，可将式(4)的第二项简化，表示为：

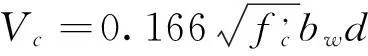
(5)

而钢筋承担的剪力为：

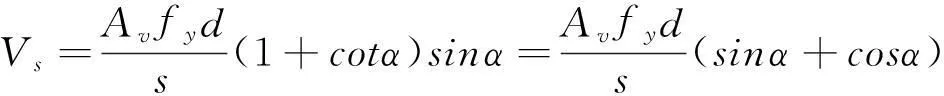
(6)

如果受剪钢筋与梁轴线垂直，即α=90°，则：

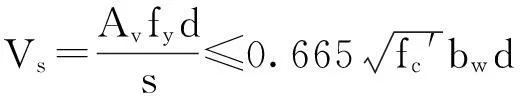
(7)

式中，Vn为名义受剪承载力，等于混凝土和箍筋承担之和，受剪承载力折减系数φ取为0.75，混凝土取圆柱体抗压强度，非预应力钢筋取屈服强度。

美国规范混凝土项承担的受剪承载力计算公式中，与我国规范不同的是，混凝土采用圆柱体抗压强度，同时还考虑了纵向受拉钢筋的影响，但其简化计算方法并没有考虑。钢筋项承担的受剪承载力计算公式中采用钢筋的屈服强度。从公式整体上看，两国公式均采用混凝土项及箍筋项受剪承载力两者之和的形式，并没有考虑两者的相关性，但美国规范公式较简单，我国规范公式较为复杂。

2试验概况

试验共浇筑11根配置HRBF500高强钢筋为箍筋的混凝土梁，试验梁JQL1-JQL10为矩形简支梁，JQL11为T形简支梁。构件JQL12为矩形简支梁且箍筋采用HRB400钢筋，以此作为对比构件。在11根高强箍筋混凝土梁的参数设计中，考虑上述规范公式及混凝土梁受剪影响因素，分别变化混凝土强度、剪跨比、配箍率、纵筋配筋率及截面形状等因素，试验构件配筋如图3、图4所示，配筋详细参数如表1所示。

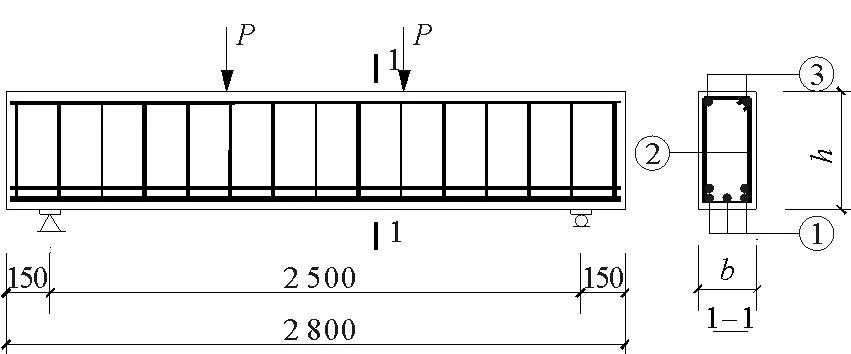
图3　矩形简支梁

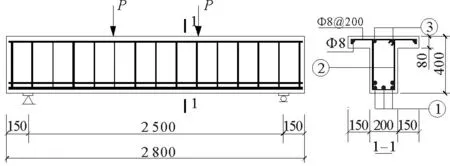
图4　T形简支梁

表1　试验构件详细参数表

对现场浇筑混凝土预留试块，测得混凝土平均强度。针对试验中所采用的HRBF500高强钢筋，选取试件进行钢筋拉伸试验，测定其强度指标，如图5所示。实测钢筋强度见表2，实测混凝土平均强度见表3，所得应力-应变曲线如图6所示。

图5　钢筋拉伸试验

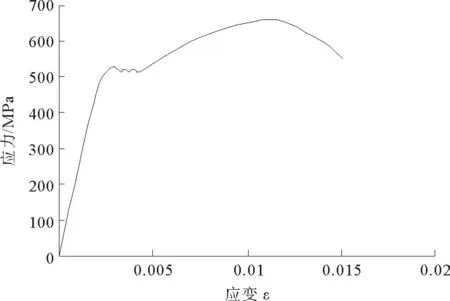
图6　HRBF500钢筋应力-应变曲线

表2　钢筋强度参数表

表3　构件混凝土强度参数表

试验构件均在结构试验室内部现场绑扎钢筋、布置传感器、支护模板、浇筑混凝土及养护。构件采用三分点集中单向加载，主加载设备采用500 t压力试验机，采用机械阀门施加荷载，采用数显设备实时监控荷载变化。构件的钢筋绑扎、模板支护、混凝土浇筑如图7、图8所示。试验过程严格按照《混凝土结构试验方法标准》(GB/T50152-2012)[12]相关规定进行。

图7　钢筋骨架及模板

图8　混凝土现场浇筑

3承载力对比分析

3.1试验现象

对于本次试验，11根配置HRBF500高强钢筋为箍筋的混凝土梁均发生了典型剪压破坏。加载初期，荷载较小，构件仅在跨中纯弯段出现若干条垂直裂缝，且裂缝宽度和长度都不大；随着荷载的增加直到结构发生破坏，纯弯段垂直裂缝宽度和长度发展均较缓慢，始终保持较小长度和宽度，且新增垂直裂缝较少。当加载到极限荷载的30%左右时，斜裂缝以较为突然的方式出现在剪跨段，且一出现就具有较大的长度，如图9所示。长度最小的构件JQL6初始斜裂缝长度为72 mm，初始斜裂缝长度最大的构件JQL7为146 mm。但斜裂缝刚出现时宽度并不大，约为0.02～0.04 mm，仅构件JQL1、JQL6、JQL8超过0.05 mm，如图10所示。初始斜裂缝倾斜角度在30°～60°；随着荷载的增大，剪跨区内又有新的斜裂缝陆续出现，已有斜裂缝特别是支座与上部加载点连线附近的斜裂缝长度和宽度继续增加。

图9　试验梁初始斜裂缝长度

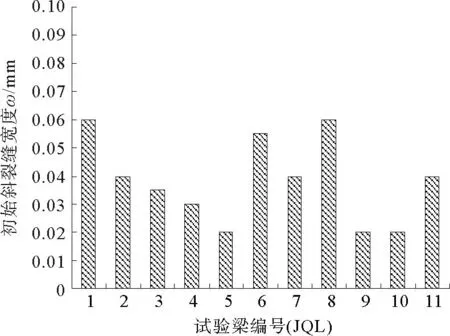
图10　试验梁初始斜裂缝宽度

当加载到极限荷载的90%以后，斜裂缝快速向两端延伸，构件整体变形明显，施加荷载值无法稳定，出现荷载无法正常均匀施加的转折点，约为极限荷载的90%～95%，荷载进一步增加，上部剪压区混凝土表面开始逐渐脱落，开始脱落物为较细的混凝土颗粒，逐渐转变成片状及小块混凝土，荷载保持快速下降趋势，最终构件上部剪压区混凝土被压碎，构件破坏。与构件JQL12对比可以发现，配置HRBF500高强钢筋混凝土梁裂缝发展规律和受剪特征与配置普通钢筋混凝土梁基本相同。考虑分配量等上部结构自重，将所得破坏荷载换算为极限剪力，如表4所示，构件实测破坏形态和裂缝扩展如图11、图12所示。

表4　实测构件极限破坏剪力

图11　试验梁JQL2破坏形态

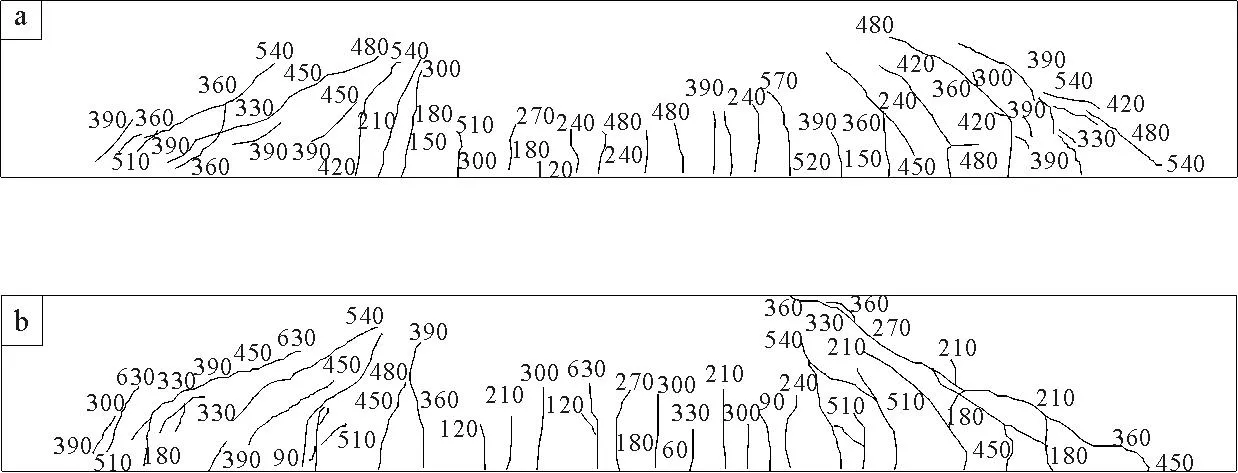
图12　试验梁JQL2裂缝扩展图

试验实测极限剪力最大值为构件JQL2，为330 kN，最小值为构件JQL10，为151 kN。由表中数据可见，T形截面梁JQL11的极限破坏剪力为326 kN，与同等参数矩形梁相比，其极限承载力提高约20.2%。由此可见，在计算过程中没有考虑受压翼缘的作用，而T形截面梁由于受压翼缘的存在，使构件剪压区混凝土的压应力和剪应力减小，极限承载力得到一定提高。

3.2承载力计算结果对比分析

根据我国混凝土规范公式(式(2))的规定，取混凝土轴心抗拉强度和钢筋抗拉强度设计值，求得构件的受剪承载力设计值Vs1；同时依据美国规范，参照式(4)，(5)，(7)的规定，取混凝土圆柱体抗压强度及钢筋屈服强度，得依照美国规范的构件受剪承载力Vs2。将规范公式计算所得受剪承载力分别与构件实测极限破坏剪力Vu对比，所得结果如图13、图14所示。

图13　采用两国规范所得受剪承载力与实测剪力

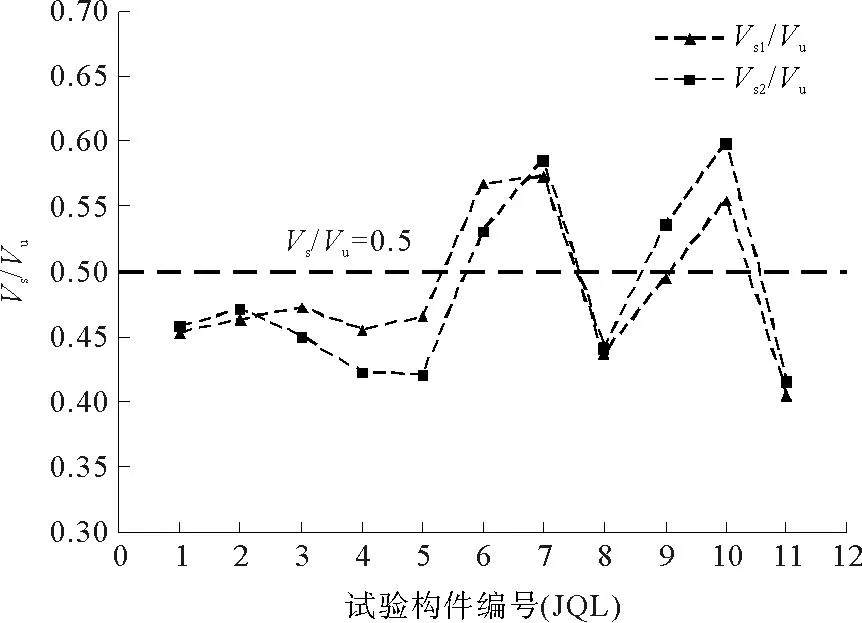
图14　采用两国规范计算所得受剪承载力与实测极限剪力对比曲线

由图13分析可知，无论采用我国规范公式还是美国规范公式，计算所得受剪承载力设计值均小于实测值，且具有较大安全余量。由于两规范受剪承载力公式考虑因素不同，我国规范(式2)中考虑了剪跨比的影响，试验构件JQL5、JQL6及JQL7无论是实测值还是计算值，随着剪跨比的增大逐渐减小。由图13分析也可以发现，对于本次试验，依据美国规范公式计算所得受剪承载力结果略小于依据我国规范公式计算结果。将图13所得规范公式计算值分别与实测值相比，得到如图14所示的Vs/Vu(Vs为设计值)对比曲线。由图14分析可知，依据我国规范计算所得受剪承载力计算值与实测值比值Vs1/Vu的均值为0.495，变异系数为0.115，其中Vs1/Vu比值最大值为构件JQL7，为0.573；Vs1/Vu比值最小值为构件JQL11，为0.404。根据美国规范计算所得受剪承载力计算值与实测值比值Vs2/Vu均值为0.484，变异系数为0.138，其中Vs2/Vu比值最大值为构件JQL10，为0.598；Vs2/Vu比值最小值为构件JQL11，为0.416。依据我国规范公式计算结果中，构件JQL6、JQL7及JQL10的Vs1/Vu比值大于0.5，而依据美国规范公式计算结果中JQL6、JQL7、JQL9及JQL10等四个构件的Vs1/Vu比值大于0.5。相同的是，依据两国规范公式计算结果中，Vs/Vu比值最小值均为T形梁JQL11，这与配置普通钢筋混凝土构件规律是一致的，主要是在计算受剪承载力的过程中没有考虑翼缘的作用。由此可见，两国规范的受剪承载力计算均比较保守，有较大的安全余量，且两国规范受剪承载力的安全储备程度比较接近。

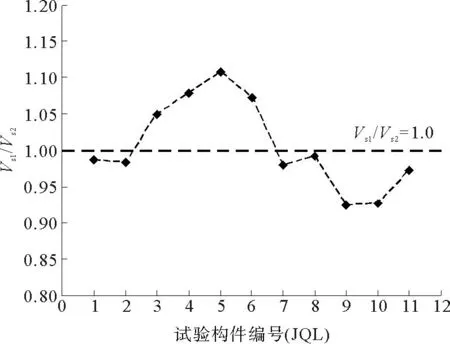
图15　采用两国规范计算所得受剪承载力Vs1/Vs2比值

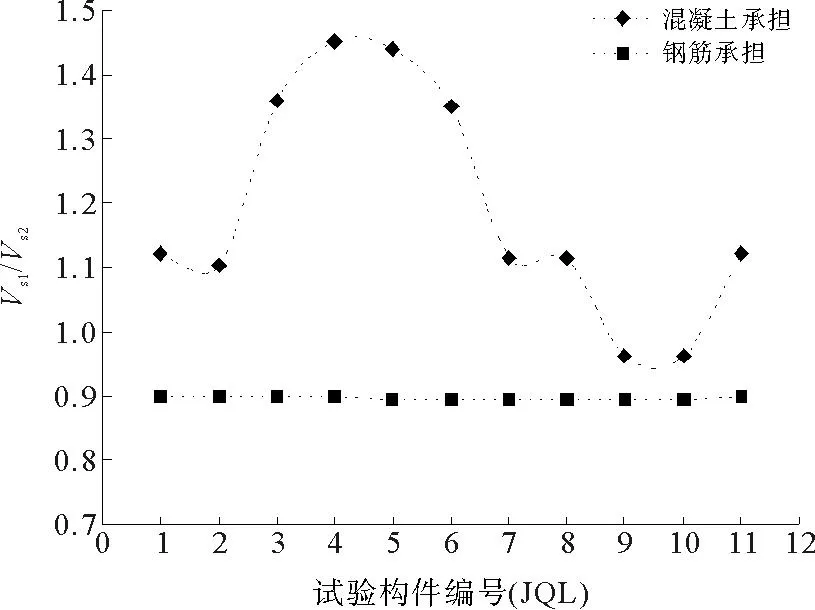
图16　采用两国规范计算所得分别由混凝土项和钢筋项承担剪力Vs1/Vs2比值

图15为采用两国规范计算所得受剪承载力Vs1/Vs2比值，图16为采用两国规范公式计算所得分别由混凝土项和钢筋项承担的剪力Vs1/Vs2比值。由图15分析可知，Vs1/Vs2比值均值为1.026，变异系数为0.061，即针对本次试验，配置高强钢筋混凝土试验构件，依据我国规范公式计算所得受剪承载力略大于美国规范公式所得结果，其中Vs1/Vs2比值最大值为构件JQL5，为1.107，Vs1/Vs2比值最小值为构件JQL9，为0.924。将规范公式计算所得受剪承载力分别由混凝土项承担和钢筋项承担表示，如图16所示。对于钢筋项承担受剪承载力，中美两国规范Vs1/Vs2比值均值为0.897，而变异系数仅为0.004，数据离散性较小，每一项比值都接近于均值。而混凝土项承担受剪承载力，两国规范计算所得Vs1/Vs2比值均值为1.190，变异系数比钢筋项大，为0.149，有一定离散性。由此可见，针对本次试验，11根配置HRBF500高强钢筋的混凝土梁受剪承载力，依据我国规范公式计算结果略大于依据美国规范公式计算所得受剪承载力；两国规范公式计算所得受剪承载力，由混凝土项承担部分，我国规范计算结果较大，而钢筋项承担部分我国规范计算结果要略小于美国规范。

4结论

针对11根配置HRBF500高强钢筋的混凝土独立梁进行受剪试验，分别采用我国混凝土规范和美国混凝土规范公式计算构件的受剪承载力，并将计算值和实测值进行对比分析，主要得到以下结论：

1)配置HRBF500高强钢筋混凝土梁，在剪跨比1.5<λ<3范围内均产生典型剪压破坏形态，裂缝发展规律和受剪特征与配置普通钢筋混凝土梁基本相同。

2)对于配置高强钢筋的混凝土梁，采用两国规范公式所得受剪承载力均小于实测值，多数构件计算承载力与试验实测值比值小于0.5，由此可见两国规范的受剪承载力计算均比较保守，有较大的安全余量，且两国规范受剪承载力的安全储备程度比较接近。

3)针对本研究11根配置HRBF500高强钢筋的混凝土梁受剪承载力，我国规范公式计算结果略大于美国规范公式计算所得；两国规范公式计算所得受剪承载力，由混凝土项承担部分，我国规范计算结果较大，而钢筋项承担部分我国规范计算结果要略小于美国规范。

参考文献：

[1]叶献国,于文静,蒋庆,等.500 MPa钢筋混凝土无腹筋梁抗剪试验研究[J].工业建筑,2012,42(11):11-15.

YE Xianguo,YU Wenjing,JIANG Qing，et al.Experimental study on shear behavior of high-strength concrete and HRBF500 steel beams without web reinforcement[J].Industrial Construction,2012,42(11):11-15.

[2]马恒蕾,王命平,耿树江,等.500 MPa细晶粒箍筋混凝土梁抗剪试验研究[J].四川建筑科学研究,2011,37(5):22-25.

MA Henglei,WANG Mingping,GENG Shujiang，et al.Experimental study on shear of reinforced concrete beam with 500 MPa hot rolled bars of fine grains as stirrups[J].Sichuan Building Science,2011,37(5):22-25.

[3]戎贤,孙永成,任泽民.HRB500钢筋混凝土受剪承载力分析[J].自然灾害学报,2008,17(1):197-201.

RONG Xian,SUN Yongcheng,REN Zemin.Analysis of shear bearing capacity of HRB500 reinforced concrete beams[J].Journal of Natural Disasters,2008,17(1):197-201.

[4]王铁成,李艳艳,戎贤,等.集中荷载下高强箍筋混凝土梁的抗剪性能[J].自然灾害学报,2006,15(5):172-177.

WANG Tiecheng,LI Yanyan,RONG Xian，et al.Shear behavior of reinforced concrete beam with high-strength stirrup under concentrated load[J].Journal of Natural Disasters,2006,15(5):172-177.

[5]贡金鑫,魏巍巍,胡家顺.中美欧混凝土结构设计[M].北京:中国建筑工业出版社,2007:118-130.

[6]徐有邻,王晓锋,刘刚,等.混凝土理论发展及规范修订的建议[J].建筑结构学报,2007,28(1):1-6.

XU Youlin,WANG Xiaofeng,LIU Gang，et al.The proposal of concrete structure theory development and code amendment [J].Journal of Building Structures,2007,28(1):1-6.

[7]林双平,苗明明,张岩,等.建筑用高强抗震钢筋[J].金属热处理,2012,37(7):102-105.

LIN Shuangping,MIAO Mingming,ZHANG Yan，et al.High-strength aseismic reinforcement steel bar for building[J].Heat Treatment of Metals,2012,37(7):102-105.

[8]王静,王命平,耿树江.HRBF500钢筋混凝土柱的受压试验研究[J].工程力学,2011,28(10):152-157.

WANG Jing,WANG Mingping,GENG Shujiang.The experimental research of reinforced concrete column by HRBF500 bars[J].Engineering Mechanics,2011,28(10):152-157.

[9]刘家慧,白娟,刘立新.细晶高强钢筋混凝土梁受剪性能试验研究[J].工业建筑,2010,40(10):106-110.

LIU Jiahui,BAI Juan,LIU Lixin.Experimental study on shear behavior of concrete beams reinforced by hot rolled ribbed bars of fine grains[J].Industrial Construction,2010,40(10):106-110.

[10]中华人民共和国国家标准.GB 50010-2010,混凝土结构设计规范[S].

[11]American Concrete Institute.Building code requirements for structural concrete(ACI 318-11)and Commentary[S].

[12]中华人民共和国国家标准.GB/T 50152-2012,混凝土结构试验方法标准[S].

(责任编辑：吕海亮)

Comparative Analysis of Shear Capacity of Concrete Beam Reinforced with High Strength Rebar Based on Chinese and American Codes

LI Peng1,2,ZHENG Hongfei1,2,ZHANG Xiantang1,2,LIU Feng1,2,WANG Fei1,2,LIU Jingwei3,ZHANG Yongbo4

(1.College of Architecture and Civil Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China； 2.Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation,Shandong University of Science and Technology,Qingdao,Shandong 266590,China；3.Qingdao Engineering Consulting Institute, Qingdao,Shandong 266071,China；4.National Oceanographic Center of Qingdao,Qingdao,Shandong 266100,China)

Abstract:An experiment on the shear behavior of 11 concrete independent beams reinforced with HRBF500 high strength rebar was carried out in the structural laboratory.Based on the experimental data,the shear capacity of the test beams was calculated by Chinese code and American code respectively.And the calculated value and measured value were compared.The results indicate that the concrete beams reinforced with HRBF500 rebar have the same crack progression and shear features as the common reinforced concrete beams.The calculated values of shear capacity by both Chinese code and American code are less than the measured value,indicating enough safety margin and similar degree of safety reserve.The shear capacity result calculated by Chinese code is slightly larger than that calculated by American code.The shear bearing capacity of concrete calculated by Chinese code is bigger while the shear bearing capacity of rebar is slightly smaller than those calculated by American code.

Key words:high strength rebar;concrete beam;Chinese code and American code;shear capacity;comparative analysis

收稿日期：2015-09-06

基金项目：国家自然科学基金项目(51208289)；山东省自然科学基金项目(ZR2013EEM023)；山东省优秀中青年科学家科研奖励基金项目(BS2015HZ017)；山东省土木工程防灾减灾重点实验室开放课题基金项目(CDPM2013ZR01)；青岛市博士后研究人员应用研究项目(01020120406)；山东科技大学人才引进科研启动基金项目(2013RCJJ032)

作者简介：李朋(1984—)，男，山东邹城人，讲师，博士，主要从事海洋工程结构动力分析、设计及防灾减灾技术研究. E-mail：lipeng@sdust.edu.cn

中图分类号：TU375.1

文献标志码：A

文章编号：1672-3767(2016)01-0066-07