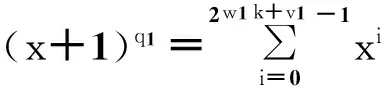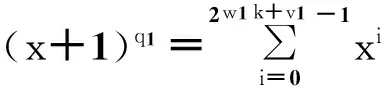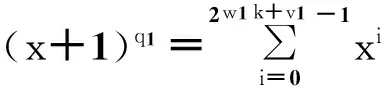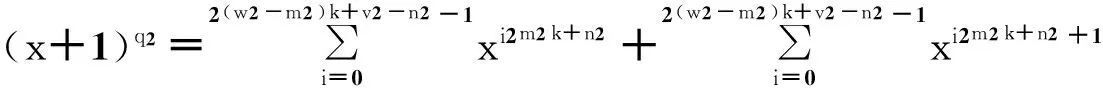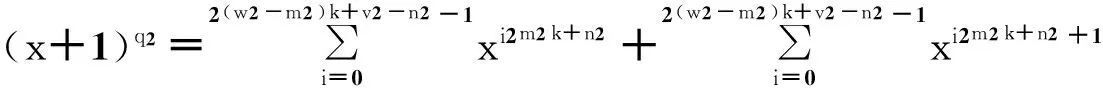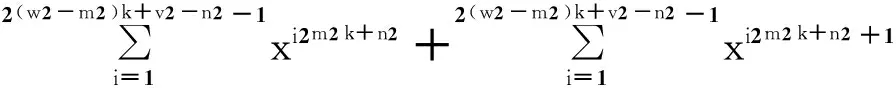扩展的WG序列线性复杂度的研究

叶　婷,陈克非,3,沈忠华,孟　倩,张文政

(1. 杭州师范大学理学院, 浙江 杭州 310036； 2. 保密通信重点实验室, 四川 成都 610041；3. 杭州市密码与网络安全重点实验室, 浙江 杭州 310036)

扩展的WG序列线性复杂度的研究

叶婷1,2,陈克非1,2,3,沈忠华1,3,孟倩1,3,张文政2

(1. 杭州师范大学理学院, 浙江 杭州 310036； 2. 保密通信重点实验室, 四川 成都 610041；3. 杭州市密码与网络安全重点实验室, 浙江 杭州 310036)

摘要：Welch-Gong(WG)序列是一类具有良好随机性的二元序列，由特定的五项式通过WG变换产生.文章将WG变换中特定的五项式推广成一般的三项式，对基于三项式的WG序列的线性复杂度展开研究, 找到了几类指数的一般形式，能使序列的线性复杂度为指数级增长, 为三项式在WG变换中的应用提供了多种选择.

关键词：WG序列;三项式;随机性;线性复杂度

0引言

伪随机序列是流密码系统的核心, 作为密钥流、随机数生成的重要手段, 有着广泛的应用. 多年来, 如何生成好的伪随机序列一直是密码学研究的重点, 也是密码学中许多理论和应用的基础与前提.

对m序列的研究始于20世纪50年代, 对于n级LFSR, 它具有最大长度周期2n-1, 除了线性复杂度外, 其他随机特性都好. 正是因为m序列的线性复杂度太小, 所以不能直接用于流密码系统的密钥流序列. 根据Berlekamp-Massey(简称B-M算法): 如果序列的线性复杂度为n, 则只需要2n个连续比特就可以恢复出全部的序列[1]. 线性复杂度较高的序列能够抵抗应用B-M算法产生的攻击.

由Golomb, Gong和Gaal在1998年研究的Welch-Gong(WG)序列是一类具有良好随机性的序列，包括长周期、0, 1分布均匀、理想的2元分布、二值自相关、与m序列三值互相关、指数级增长的线性复杂度等. 2005年, Nawaz和Gong首次提出了WG序列密码, 并且作为欧洲eSTREAM计划候选对象之一[2]. 之后2个轻量级的WG序列密码相继提出, 分别是WG-7[3]和WG-8[4]. 最近, Fan等[5]提出使用WG-16密码体制来保证4G网络的安全性与完整性. 基于WG变换产生的同步流密码不仅具有很好的随机性, 也能抵抗一些攻击来保证安全性, 这类密钥流一般可通过硬件实施产生. 由于WG序列良好的密码学性质, 至今被用在各个领域且引起很多国内外学者的进一步研究.

原WG序列是由特定的五项式通过WG变换产生的. 针对WG变换, 一般研究的是奇数项式, 若能把特定的五项式推广到一般的三项式、五项式、七项式乃至任意的奇数项式并且产生的序列仍具有良好的随机性, 便能得到一系列更多的伪随机序列, 也为伪随机序列的应用提供更多的选择. 考虑到多项式通过WG变换的复杂程度, 本文将WG变换中特定的五项式推广成一般的三项式, 产生的序列依然能保持较好的随机性. 但序列的线性复杂度的增长与三项式中各项的指数有关, 选取好的指数能使线性复杂度呈现指数级增长. 因此，本文对基于三项式的WG序列的线性复杂度展开全面研究, 找到了几类指数的一般形式，能使序列的线性复杂度为指数级增长, 为三项式在WG变换中的应用提供了多种选择.

1预备知识

设F(q)=GF(q), 则a={ai}, ai∈F2表示F2上的二元序列.序列a={ai}的线性复杂度是指产生此序列的LFSR的最小阶数, 记为LS(a).

定义1[1]F=GF(qn), K=GF(q), 迹函数TrF/K(x)定义如下:TrF/K(x)=x+xq+…+xqn-1, x∈F.TrF/K(x)是一个从F到K的映射函数. 当q=2时, TrF/K(x)可简写成Tr(x): Tr(x)=x+x2+…+x2n-1,x∈GF(2n). Tr(x)的取值为0或1.

定义2[6]令h(x)=x+xt1+xt2+xt3+xt4, x∈F2n.

其中n, k均为正整数, Tr(h(x))的WG变换为:f(x)=Tr(h(x+1)+1), x∈F2n.

2序列的线性复杂度

2.1原WG序列的线性复杂度

定理1[7]f(x)=Tr(h(x+1)+1)=∑i∈ITr(xi), 则

由推论1, 以下对基于三项式的WG序列的线性复杂度展开研究.

2.2基于三项式的WG序列的线性复杂度

令g(x)=x+xq1+xq2, f(x)为Tr(g(x))的WG变换, 即

f(x)=Tr(g(x+1)+1), x∈F2n(n=2k-1或2k).

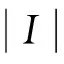
2.2.1指数个+非指数个

即(x+1)q1的展开式为指数个，(x+1)q2的展开式为非指数个.

1)q1=2w1k+v1-1,q2=2w2k+v2+1(w1

(x+1)q2=x2w2k+v2+1+x2w2k+v2+x+1.

LS=2w1k+v1+1.

2)q1=2w1k+v1-1,q2=2w2k+v2+2m2k+n2+1(w1

(x+1)q2=x2w2k+v2+2m2k+n2+1+x2w2k+v2+2m2k+n2+x2w2k+v2+1+x2m2k+n2+1+x2w2k+v2+x2m2k+n2+x+1.

Tr(g(x+1)+1)=Tr(x2w2k+v2+2m2k+n2+1+x2w2k+v2+2m2k+n2+x2w2k+v2+1+x2m2k+n2+1+

LS=2w1k+v1+5.

(x+1)q2=x2w2k+v2+1+x2w2k+v2+x+1.

LS≈2(w1-m1)k+v1-n1+1.

4)q1=2w1k+v1-2m1k+n1+1,q2=2w2k+v2+2m2k+n2+1(w1

(x+1)q2=x2w2k+v2+2m2k+n2+1+x2w2k+v2+2m2k+n2+x2w2k+v2+1+x2m2k+n2+1+x2w2k+v2+x2m2k+n2+x+1.

Tr(g(x+1)+1)=Tr(x2w2k+v2+2m2k+n2+1+x2w2k+v2+2m2k+n2+x2w2k+v2+1+x2m2k+n2+1+x2w2k+v2+

LS≈2(w1-m1)k+v1-n1+1+5.

2.2.2指数个+指数个

即(x+1)q1与(x+1)q2的展开式都为指数个.

1)q1=2w1k+v1-1,q2=2w2k+v2-1(w1

LS=2w2k+v2-2w1k+v1+1.

2)q1=2w1k+v1-1,q2=2w2k+v2-2m2k+n2+1(w1

LS=2w1k+v1+2(w2-m2)k+v2-n2+1-3.

3)q1=2w1k+v1-2m1k+n1+1,q2=2w2k+v2-2m2k+n2+1(w1

LS=2(w1-m1)k+v1-n1+1+2(w2-m2)k+v2-n2+1-3.

例1和例2是研究三项式的过程中找到的两个具体的例子,其中例1为指数级增长,例2为线性级增长.

例1g(x)=x+xq1+xq2,x∈F2n,n=2k-1或2k,q1=2k+1+2k+1，q2=2k-1.

(x+1)2k+1+2k+1=x2k+1+2k+1+x2k+1+2k+x2k+1+1+x2k+1+x2k+1+x2k+x+1.

例2g(x)=x+xq1+xq2,x∈F2n,n=2k-1或2k,q1=2k+1，q2=2k-1+1.则

(x+1)2k+1=x2k+1+x2k+x+1.

(x+1)2k-1+1=x2k-1+1+x2k-1+x+1.

f(x)=Tr(g(x+1)+1)=Tr(x+x2k-1+x2k-1+1+x2k+x2k+1).

所以序列b的线性复杂度为LS(b)=LS(f(x))=5n.

3总结

参考文献:

[1] 郭鑫.伪随机序列构造及其随机性分析研究[D]. 上海：上海交通大学,2008.

[2] eSTREAM. The ECRYPT stream cipher project[EB/OL]. [2015-06-02]. http://www.ecrypt.eu.org/stream/.

[3] LUO Y, CHAI Q, GONG G, et al. WG-7: a lightweight stream cipher with good cryptographic properties[C]//IEEE.IEEE Global Communications Conference-GLOBECOM. Florida：[s.n.]，2010:1-6.

[4] FAN X X, MANDAL K, GONG G. WG-8: A lightweight stream cipher for resource-constrained smart devices[M]. Quality, Reliability, Security and Robustness in Heterogeneous Networks. Heidelbergs: Springer,2013:617-632.

[5] FAN X X, WU T, GONG G. An efficient stream cipher WG-16 and its application for securing 4G-LTE networks[J]. Applied Mechanics & Materials,2014(490/491):1436-1450.

[6] GONG G, YOUSSEF A M. Cryptographic properties of the Welch-Gong transformation sequence generators[J]. IEEE Transactions on Information Theory,2002,48(11):2837-2846.

[7] NO J S, GOLOMB S W, GONG G, et al. Binary pseudorandom sequences of period 2n-1 with ideal autocorrelation[J]. IEEE Transactions on Information Theory,1998,44(2):814-817.

On the Linear Span of the Extended WG Sequences

YE Ting1,2, CHEN Kefei1,2,3, SHEN Zhonghua1,3, MENG Qian1,3, ZHANG Wenzheng2

(1. School of Science, Hangzhou Normal University, Hangzhou 310036, China；2. Science and Technology on Communication Security Laboratory, Chengdu 610041, China；3. Hangzhou Key Laboratory of Cryptography and Network Security, Hangzhou 310036, China.)

Abstract:Welch-Gong(WG) sequences have good randomness. The original WG sequences are generated by a specific five-term function through WG transformation. This paper extends the specific five-term function to general three-term function in WG transformation, and studies the linear span of WG sequences based on three-term function. Some general forms of the indexes, which can make linear span increase exponentially are found. This provides a variety of options for the applications of three-term function in the WG transformation.

Key words:WG sequences; three-term function; randomness; linear span

收稿日期：2015-08-22

基金项目：国家自然科学基金项目(61472114); 保密通信重点实验室基金项目(9140C110203140C11049).

通信作者：陈克非(1959—),男,教授,博士，主要从事密码学与信息安全研究.E-mail:kfchen@hznu.edu.cn

doi:10.3969/j.issn.1674-232X.2016.03.010

中图分类号:TP309MSC2010: 94A60

文献标志码:A

文章编号:1674-232X(2016)03-0277-05