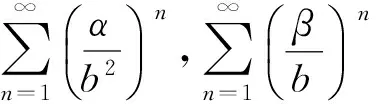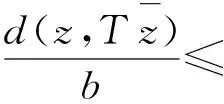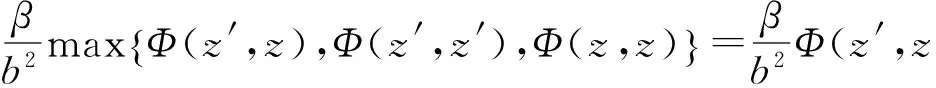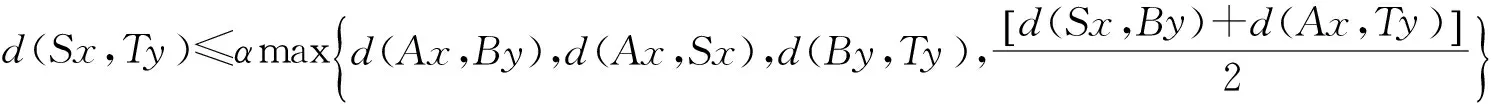b-度量空间中两对自映象的公共不动点定理

方楠楠，谷　峰

(杭州师范大学理学院，浙江 杭州 310036)

b-度量空间中两对自映象的公共不动点定理

方楠楠，谷峰

(杭州师范大学理学院，浙江 杭州 310036)

摘要：在完备b-度量空间的框架下，讨论了一类新的压缩型映象，证明了此类映象公共不动点的存在性和唯一性，获得了一个新的公共不动点定理，推广和发展了原有的结果.

关键词：相容映象；自映象；弱相容；b-度量空间；公共不动点

1预备知识

1993年，Czerwik[1]首次提出了b-度量空间的概念，此后，许多人研究了该空间中的不动点问题，得到了一些有重要意义的研究结果[1-6].2009年，李亚琼等[7]在度量空间中研究了两对相容映象的一个公共不动点问题, 在某些条件下，证明了一个新的公共不动点定理. 本文的目的是把文[7]在度量空间中的相应结果推广到b-度量空间之中.

定义1[1]设X是一个非空集合，b≥1是一个给定的实数. 称函数d:X×X→R+是集合X上的一个b-度量，若∀x,y,z∈X，有以下条件被满足:

(ii)d(x,y)=d(y,x);

(iii)d(x,y)=b[d(x,z)+d(z,y)].

这时称(X,d)是一个b-度量空间，实数b≥1称为该b-度量空间的系数.

注1当b=1时，b-度量空间即为通常的度量空间，但一般情况下，b-度量空间未必是度量空间，如文[2]中例3.1.

注2集合X上的一个b-度量不一定连续，如文[3]中例1.3.

定义2[4]设(X,d)是b-度量空间，{xn}⊂X，

(ii)若d(xn,xm)→0(n,m→∞),则称{xn}为X中的一个b-Cauchy列.

注3[4]每个b-收敛点列的极限是唯一的，而且每个b-收敛点列都是b-Cauchy列.

定义3[4]设(X,d)是b-度量空间，如果X中的每个b-Cauchy都在X中b-收敛，则称b-度量空间(X,d)是b-完备.

定义4[5]设(f,g)是b-度量空间(X,d)上的自映象对，称(f,g)是相容的，如果∀{xn}⊂X,只要fxn→x,gxn→x(n→∞),x∈X，就有d(fgxn,gfxn)→0(n→∞).

定义5[8]集合X上的自映象对(f,g)称为是弱相容的，如果{t∈X:f(t)=g(t)}⊂{t∈X:fg(t)=gf(t)}.

注4显然，相容映象对一定是弱相容映象的，但反之不真，反例可见[8].

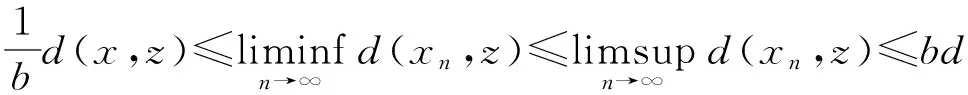
引理2[5]设(X,d)是一个b-度量空间，{xn},{yn}⊂X，若xn→t(n→∞)且d(xn,yn)→0(n→∞)，则yn→t(n→∞).

2主要结果

定理1设(X,d)是具有系数b≥1的完备b-度量空间，S,T,A,B:X→X是4个映象，设φ(x,y)是X×X到[0,∞)的对称连续函数，满足φ(x,x)=0，∀x∈X. 如果存在α,β∈[0,1)，使得以下条件成立：

(i)SX⊂BX，TX⊂AX；

(Ⅰ)A,S之一连续，(S,A)相容，(T,B)弱相容；

(Ⅱ)B,T之一连续，(T,B)相容，(S,A)弱相容.

证明由于SX⊂BX，TX⊂AX，因此∀x0∈X,∃x1∈X,使得Sx0=Bx1=y0；∃x2∈X,使得Tx1=Ax2=y1；…；∃x2n+1∈X,使得Sx2n=Bx2n+1=y2n；∃x2n+2∈X，使Tx2n+1=Ax2n+2=y2n+1；…；这样得到点列{xn}和{yn}.

下证{yn}是X中的Cauchy列.根据条件(iii)可以得到：

d(y2n,y2n+1)=d(Sx2n,Tx2n+1)≤

当d(y2n-1,y2n)≥d(y2n,y2n+1)时，

(1)

当d(y2n-1,y2n)

(2)

综合式(1)和(2)，得

(3)

同理可证

(4)

从而由式(3)和(4)可知，对一切n≥1，有

(5)

由条件(ii)可知

(6)

(7)

由式(5)和(7)得

(8)

因为对任意整数m,n,m>n，由三角不等式和式(8)，有

下面分两种情况证明z是S,T,A和B的公共不动点.

情形1设条件(Ⅰ)被满足.

因为序列{Sx2n}={Bx2n+1}={y2n}和{Tx2n-1}={Ax2n}={y2n-1}都是{yn}的子列，因此它们也收敛于z，又因为(S,A)是X上的一对相容映象，则有d(SAx2n,ASx2n)→0(n→∞).

先设A连续，则A2x2n→Az,ASx2n→Az(n→∞)，由d(SAx2n,ASx2n)→0(n→∞)及引理2知SAx2n→Az(n→∞). 根据条件(iii)可得

由引理1得

所以

d(Az,z)≤αd(Az,z)+b2φ(Az,z).

(9)

(10)

所以由式(10)及0≤β<1,b≥1易知，有φ(Az,z)=0. 将其代入式(9)中得d(Az,z)≤αd(Az,z)，由0≤α<1得d(Az,z)=0，故Az=z.

再由条件(iii)可知

由引理1知

(11)

再根据条件(iii)及Az=Sz，Tz=Bz得

综上可知，Sz=Tz=Az=Bz=z，即z是S,T,A和B的公共不动点.

再设S连续，则S2x2n→Sz,SAx2n→Sz(n→∞)，因为(S,A)是相容映象对，故d(SAx2n,ASx2n)→0(n→∞)，因此由引理2知ASx2n→Sz(n→∞).

利用条件(iii)可得

(12)

由引理1可得

由引理1得

(13)

综上可知，Sz=Tz=Az=Bz=z，即z是S,T,A和B的公共不动点.

情形2设条件(Ⅱ)被满足.这种情况与情形1的证明类同，此处省略.

最后证明z是S,T,A,B的唯一公共不动点，而且z也分别是映象对(S,A)和(T,B)的唯一公共不动点. 设z′≠z,z′∈X也是S和A的一个公共不动点，根据条件(iii)可知

(14)

再根据条件(ii)得

注5定理1不仅将[7]中定理2.1从度量空间拓广至b-度量空间，而且还将两对映象都相容减弱为一对相容另一对弱相容.

注6在定理1中取：1)φ(x,y)=0；2)A=B=I(其中I表恒等映象,下同)；3)S=T,A=B；4)S=T,A=B=I，可得到对应的新结果，此处省略.

在定理1中取b=1，则得到如下推论.

推论1设(X,d)是完备度量空间，S,T,A,B:X→X是4个映象，设φ(x,y)是X×X到[0,∞)的对称连续函数，满足φ(x,x)=0，∀x∈X. 如果存在α,β∈[0,1)，使得以下条件成立：

(i)SX⊂BX，TX⊂AX；

(Ⅰ)A,S之一连续，(S,A)相容，(T,B)弱相容；

(Ⅱ)B,T之一连续，(T,B)相容，(S,A)弱相容.

注7推论1将[7]中定理2.1的条件从两对映象都相容减弱为一对相容另一对弱相容.

参考文献:

[1] CZERWIK S. Contraction mappings inb-metric spaces[J]. Acta Math Inf Univ Ostrav,1993,1(1):5-11.

[2] AKKOUCHI M. A common fixed point theorems for expansive mappings under strict implicit conditions onb-metric spaces[J]. Acta Univ Palack Olomuc. Fac Rerum Natur. Math,2011,50(1):5-15.

[3] LATIF A, PARVANEH V, SALIMI P, et al. Various Suzuki type theorems inb-metric spaces[J]. J Nonlinear Sci Appl,2015,8:363-377.

[4] BORICEANU M. Strict fixed point theorems for multivalued operators inb-metric spaces[J]. Int J Mod Math,2009,4(3):285-301.

[5] ROSHAN J R, SHOBKOLAEI N, SEDGHI S, et al. Common fixed point of four maps inb-metric spaces[J]. Hacet J Math Stat,2014,43(4):613-624.

[6] AGHAJANI A, ABBAS M, ROSHAN J R. Common fixed point of generalized weak contractive mappings in partially orderedb-metric spaces[J]. Math Slovaca,2014,64(4):941-960.

[7] 李亚琼，谷峰.两对相容映象的一个新的公共不动点定理[J].杭州师范大学学报(自然科学版)，2009，8(4)：257-260.

[8] JUNGCK G. Common fixed points for non-continuous nonself mappings on a nonnumeric spaces[J]. Far East J Math Sci,1996,4(2):199-212.

Two Pairs of Self-image Common Fixed Point Theorem inb-metric Space

FANG Nannan， GU Feng

(School of Science， Hangzhou Normal University， Hangzhou 310036， China)

Abstract:In the framework of complete b-metric space, a type of new contractive mappings was discussed， the existence and uniqueness of the common fixed point were proved, a new common fixed theorem was obtained, the existing conclusions were extended.

Key words:compatible mappings; self-image; weakly compatible; b-metric space; common fixed point

收稿日期：2015-06-10

基金项目：国家自然科学基金项目(11071169)；浙江省自然科学基金项目(Y6110287).

通信作者：谷峰(1960—)，男，教授，主要从事非线性分析及应用研究.E-mail：gufeng99@sohu.com

doi:10.3969/j.issn.1674-232X.2016.03.011

中图分类号:O189；O177MSC2010： 47H10；54H25；55M20

文献标志码:A

文章编号:1674-232X(2016)03-0282-08