一种角反射体雷达散射截面积的高频预估算法

范学满　胡生亮　贺静波

(海军工程大学电子工程学院,武汉 430033)



一种角反射体雷达散射截面积的高频预估算法

范学满胡生亮贺静波

(海军工程大学电子工程学院,武汉 430033)

摘要几何光学/区域投影(Geometrical Optics/Area Projection,GO/AP)法是一种综合利用GO和AP进行电大尺寸目标单站雷达散射截面积(Radar Cross Section,RCS)预估的高频混合算法.文章推导建立了利用GO/AP法进行RCS预估的通用流程,计算出不同入射方向下三角形三面角反射RCS的完整表达式;将其与RCS最大值的经验公式以及FEKO软件的仿真结果进行对比,验证了GO/AP法的可行性;在边界入射方向对GO/AP算法进行改进,进一步拓宽了GO/AP法对观察角的适应范围.

关键词雷达散射截面积;几何光学/区域投影法;有效反射面积;角反射体;FEKO

引言

雷达散射截面积(Radar Cross Section, RCS)是表征军用目标的关键特性之一,是度量目标对雷达散射能力的一个重要物理量.角反射体是由两块或三块金属板构成的二面角或三面角结构,在舰艇、飞机、导弹等军用目标上经常出现,是军用目标侧视方向的强散射源,特别是当各平板相互正交时,在一个很宽的观察角范围内能够呈现出很大的RCS[1].因此,高效、准确地分析角反射体的后向散射特性,是预估各类军用目标RCS的重要基础.

两面角反射体的RCS预估算法已较为成熟,目前研究重点主要集中在三面角反射体.由于三面角反射体在实际应用中通常是电大目标或电极大目标,因此可以采用高频近似算法及相关专用软件进行RCS预估.文献[2-4]分别采用射线弹跳(Shooting and Bouncing Rays,SBR)法、高斯光束(Gaussian Beams,GB)法和复射线(Complex Rays,CR)法进行RCS预估,这三种方法对射线密度要求较高,计算量大;文献[5-6]利用物理光学(Physical Optics,PO)法进行RCS预估,需要分别计算1～3次的散射贡献,确定照亮区域的过程复杂;文献[7]综合利用戈登表面积分法和几何光学法,虽然简化了确定照亮区域的过程,但计算量依然很大;专用软件方面,FEKO、XPATCH、GRECO等电磁仿真软件也是RCS预估的有效手段[8].上述RCS预估方法,虽然均能以曲线形式给出RCS的预估结果,但均没能给出RCS的完整表达式.另外,目前国内涉及雷达散射截面的相关书籍[9-10],都只给出了角反射体RCS最大值的经典公式和相关曲线,但未给出最大值公式的推导过程,更未给出不同观察角时RCS的完整表达式.Jos Groot在文献[11]中首次提出了一种直观的RCS预估算法——GO/AP算法,并利用GO/AP法给出了三角形角反射体RCS表达式,但未给出具体的算法推导过程,国内也尚未发现研究GO/AP算法的相关文献.

GO/AP法的直观、高效性促使笔者展开进一步研究,旨在推导、建立一套利用GO/AP法进行RCS预估的通用流程,并在此基础上验证算法的有效性,改进算法的局限性.文章基于GO/AP算法的基本思想,对角反射体在不同观察角时的RCS进行推导;将所得公式与参考文献[11]中结果以及RCS最大值的经验公式进行对比,并利用FEKO软件对该算法进行仿真验证;最后,在边界入射方向对算法进行分析、改进,拓宽了算法对观察角的适应范围.

1GO/AP算法推导

三角形角反射体、方形角反射体和圆形角反射体是三类较为常见的三面角反射体.以图1所示的三角形三面角反射体为例进行算法推导,直角坐标系OXYZ由角反射体顶点O和三条交线OA、OB、OC构成.端点A、B、C决定角反射体的孔径大小,坐标分别为(L,0,0)、(0,L,0)、(0,0,L),其中L为垂直边长的长度.电磁波入射方向n=(l,m,n)=(cosα,cosβ,cosγ),其中,

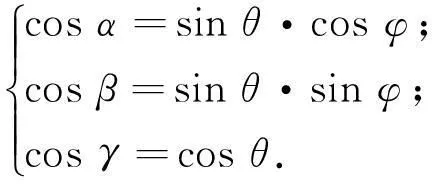
(1)

式中:θ为俯仰角,即入射方向与OZ轴夹角;φ为方位角,即入射方向在OXY平面的投影与OX轴夹角.

图1　三角形三面角反射体

GO法是波长为零的高频极限情形,这时散射现象可作为经典射线寻迹处理,遵循斯涅尔反射定律,GO法认为散射体上的“照亮点”与过该点和散射体相切的无限大平面对入射波的反射效果等效.只要目标尺寸大于波长的2～3倍,便可利用GO法进行分析.实际应用中,角反射体垂直边长通常为米/分米级,对工作在厘米波段的雷达,显然符合GO法分析要求.

如图1所示,入射波在角反射体内可能发生0～3次反射,只有三次反射回波才会按原入射方向返回雷达接收机,这些三次反射回波是角反射体RCS的最主要贡献,通常0～2次反射回波在计算单站RCS时可忽略.入射波能否发生三次反射由入射点P和入射方向共同决定.对同一平面波而言,所有三次反射回波是等相位的.因此,用GO法预估RCS时,可以将角反射体等效为过顶点垂直于入射方向的某一特定大小的平面,该平面称为“等效平面”,其面积称为“有效反射面积”,记作Aeq.这样就可以利用波长λ的平面波垂直入射平板时的RCS公式预估角反射体的RCS,即

(2)

因此,只需要确定等效平面的形状并积分求得有效反射面积Aeq,便可求得角反射体的RCS.Aeq可通过区域投影确定:将角反射体投影到过顶点O垂直于入射方向的平面上,所得投影称为“实孔径”;在投影面上,将“实孔径”绕顶点O旋转180°,得到“虚孔径”;实、虚孔径的重合区域即为Aeq.利用SolidWorks软件仿真了方位角φ=30°时,Aeq随俯仰角θ的变化情况,如图2所示,图中阴影区域为Aeq.可见Aeq是入射方向(θ和φ)的函数,随θ增大,Aeq呈现出平行四边形→六边形→平行四边形的变化过程.

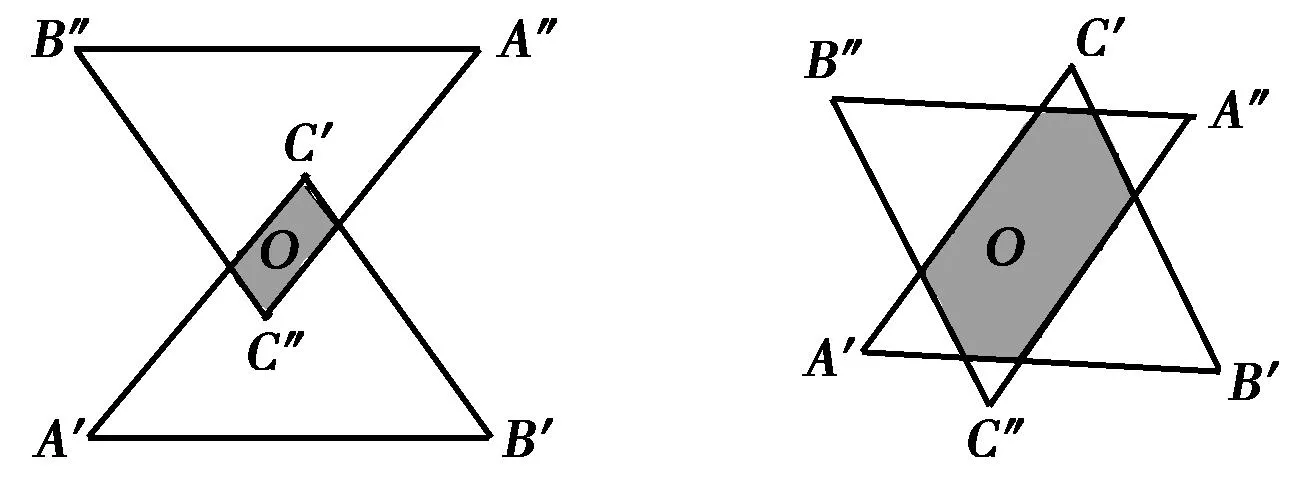
(a) θ=15°　　　　　 (b) θ=45°

(c) θ=60°　　　　　 (d) θ=75°图2　角反射体的Aeq随θ的变化情况(φ=30°)

根据对称性,只需要分析φ(0～45°)、θ(0～90°)的范围,而且只需要确定端点A、B、C的投影A′、B′、C′,三角形A′B′C′即为“实孔径”,其关于顶点O的对称三角形A″B″C″即为“虚孔径”.为方便后续面积计算,需要进行坐标变换,将投影点A′、B′、C′的坐标从坐标系OXYZ变换到OX′Y′Z′.OX′Y′Z′仍以顶点O为原点,OX′轴沿OA′方向,OZ′轴沿入射方向的相反方向,OY′轴在投影面内与OX′垂直满足右手螺旋法则.OXYZ到OX′Y′Z′的坐标变换公式为

(3)

在求Aeq过程中,只需要计算x′、y′,实际上投影点的z′≡0.

利用式(3)求得A′～C′和A″～C″在坐标系OX′Y′Z′下的坐标后,即可求得围成实、虚孔径的6条边界线(A′B′、A′C′、B′C′、A″B″、A″C″、B″C″)的方程:

y'= kn·x'+cn,kn=y'i-y'jx'i-x'j

,

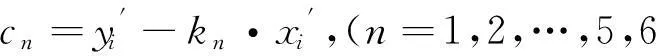
(4)

从而根据入射角度确定有效平面的顶点,这些顶点由实、虚孔径的顶点和实、虚孔径的边线交点组成.例如φ=30°,θ=75°时,等效平面由A′C′与A″B″的交点、A″C″与A′B′的交点、点A′、点A″这四个点确定.当确定顶点后利用MATLAB的polyarea函数便可求得Aeq,将Aeq带入式(2)即可求得RCS.

综上所述,推导建立了利用GO/AP算法进行RCS预估的通用流程,如图3所示.

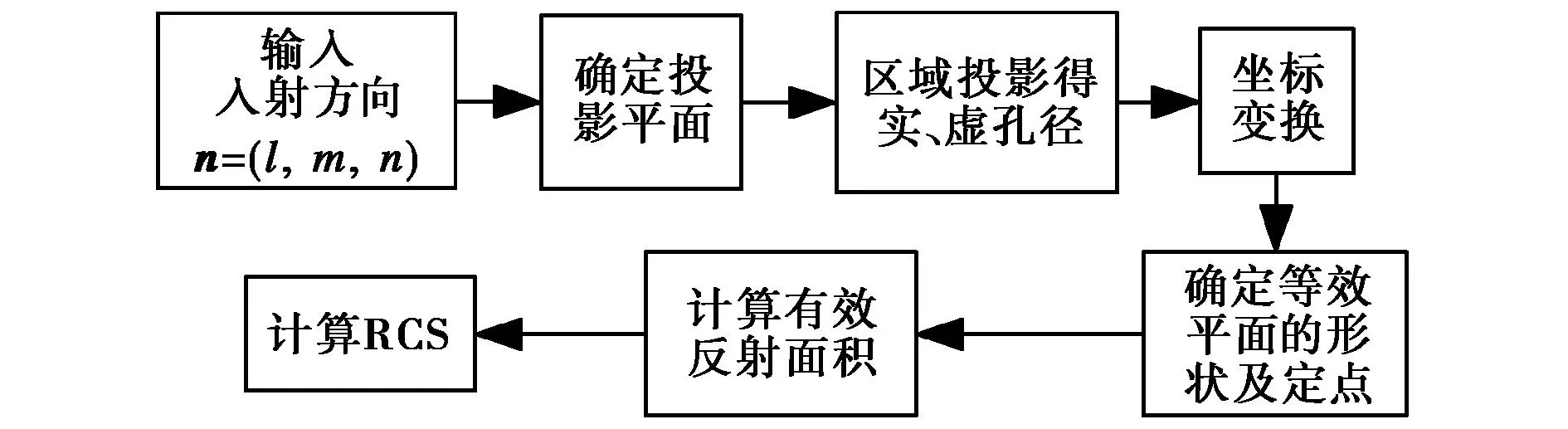
图3　GO/AP算法流程

2GO/AP算法RCS预估结果

根据实(虚)孔径的顶点与虚(实)孔径中相对边线的重合关系,以顶点位于相应边线为临界点,可将入射方向以曲线A、B为界划分成三个区域,如图4所示,区域1、3中的有效反射面积为平行四边形,区域2中为六边形.

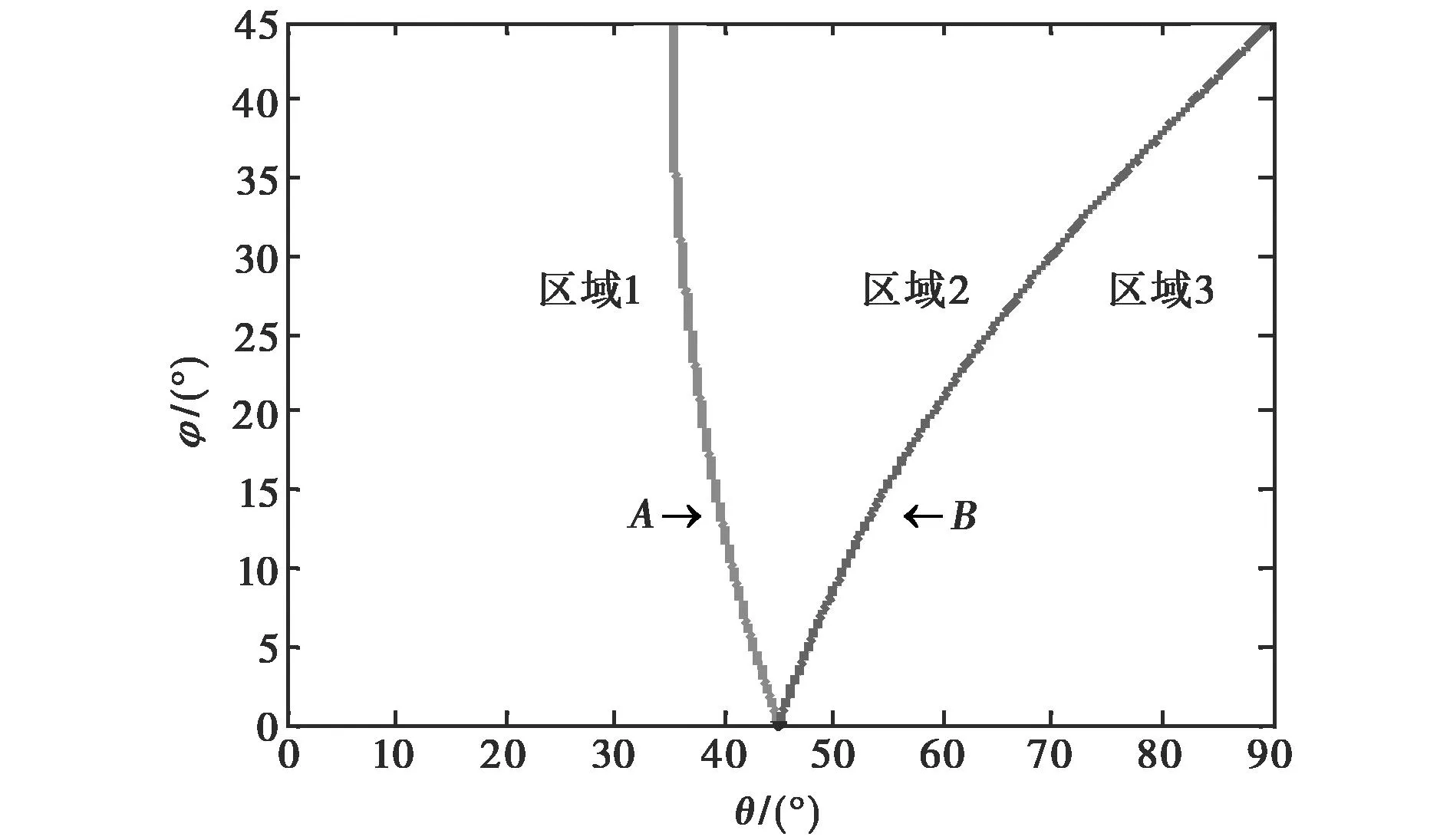
图4　三角形三面角反射体的入射方向分区

曲线A和B的方程为:

cotθ=2sin(φ+45°) (A,θ=35.26°～45°);2cos(φ+45°) (B,θ=45°～90°).{

(5)

按照第一部分的思路推导得Aeq在三个区域中的表达式分别为:

(6)

式中:f(θ,φ)≡sinθ·(cosφ+sinφ)+cosθ.式(6)在0°≤θ≤90°∩0°≤φ≤45°范围内有效;根据对称性,当45°<φ≤90°时,只需要将式(6)中的φ替换为90°-φ即可.式(6)与参考文献[11]中给出的结果一致,说明文中的推导过程正确.综合式(6)和式(2),得到三角形三面角反射体在垂直边长1 m、入射波频率10 GHz条件下,0°≤θ≤90°∩0°≤φ≤90°入射角范围内的RCS预估结果,如图5所示.

图5　三角形三面角反射体的RCS预估结果

3GO/AP算法验证及改进

首先,计算电磁波沿角反射体中心轴方向入射时的RCS,将φ=45°和θ=54.75°代入式(6)和式(2),得角反射体RCS最大值的计算公式为

(7)

式(7)与参考文献[9]中RCS最大值的经验公式一致,说明GO/AP算法对RCS最大值的计算有效.

选取FEKO7.0电磁仿真软件中的几何光学/射线追踪算法(GeometricalOptics/RayLaunching,GO/RL)作为验证工具,仿真环境为Intel(R)Core(TM)i5-4590、4G内存.选取θ=60°∩0°≤φ≤90°和φ=15°∩0°≤θ≤90°两种情况,对比FEKO和GO/AP算法的RCS预估结果,如图6所示.

从图6可知,GO/AP算法在2°≤θ≤88°∩2°≤φ≤88°入射方向角范围内与FEKO计算结果具有很好的一致性,但在θ和φ接近0°和90°的边界入射方向处,GO/AP算法有待改进.因为GO/AP算法是基于三次反射来计算有效反射面积Aeq,在2°≤θ≤88°∩2°≤φ≤88°入射方向范围内,三次反射是单站RCS的主要贡献,相比之下一次、二次反射分量可忽略不计;而在θ和φ趋近0°和90°的边界入射方向时不再有三次反射,相反一次或二次反射成为不可忽视的主要成分.因此,需要对θ和φ趋近0°和90°的情况进行改进.从图6可知,在边界值处RCS几乎在2°范围内由接近0跃升至一个上千平方米的峰值,所以用一条过峰值的直线来预估这2°范围内的RCS比较合理.下面分析边界入射方向时的峰值.

(a) θ=60°∩0°≤φ≤90°时的对比图

(b) φ=15°∩0°≤θ≤90°时的对比图图6　GO/AP算法与FEKO预估结果对比

1) θ=0°

此时入射波垂直照射底面(OAB),两个侧面不起作用,可以按三角形平板的RCS公式进行计算,即

(8)

式中:L为角反射体的垂直边长;λ为入射波长.

2)θ=90°

此时入射波垂直OZ轴(OC边)入射到角反射体的两个侧面,底面(OAB)不起作用,三面角反射体等价于由两个三角形侧面构成的两面角反射体,根据参考文献[13],推导可得

(9)

式中:φ为入射波方位角.

3)φ=0°或90°

与θ=90°类似,φ=0°时,三面角反射体等价于以OB为公共边的两面角反射体;φ=90°时,三面角反射体等价于以OA为公共边的两面角反射体.此时,

(10)

式中:θ为入射波俯仰角.

综上所述,可分别求出θ和φ等于0°或90°时的峰值,利用过峰值的一条直线对边界入射方向的RCS进行预估,改进GO/AP算法对边界入射方向的不适应性.如图7所示，改进后的GO/AP算法与FEKO的计算结果具有很好的一致性.需要指出的是改进后的GO/AP算法也只在0°≤θ≤90°∩0°≤φ≤90°有效,其他方向的RCS值不存在多次反射贡献,可由平板的散射场直接给出[13].

(a) θ=60°∩0°≤φ≤90°时的对比图

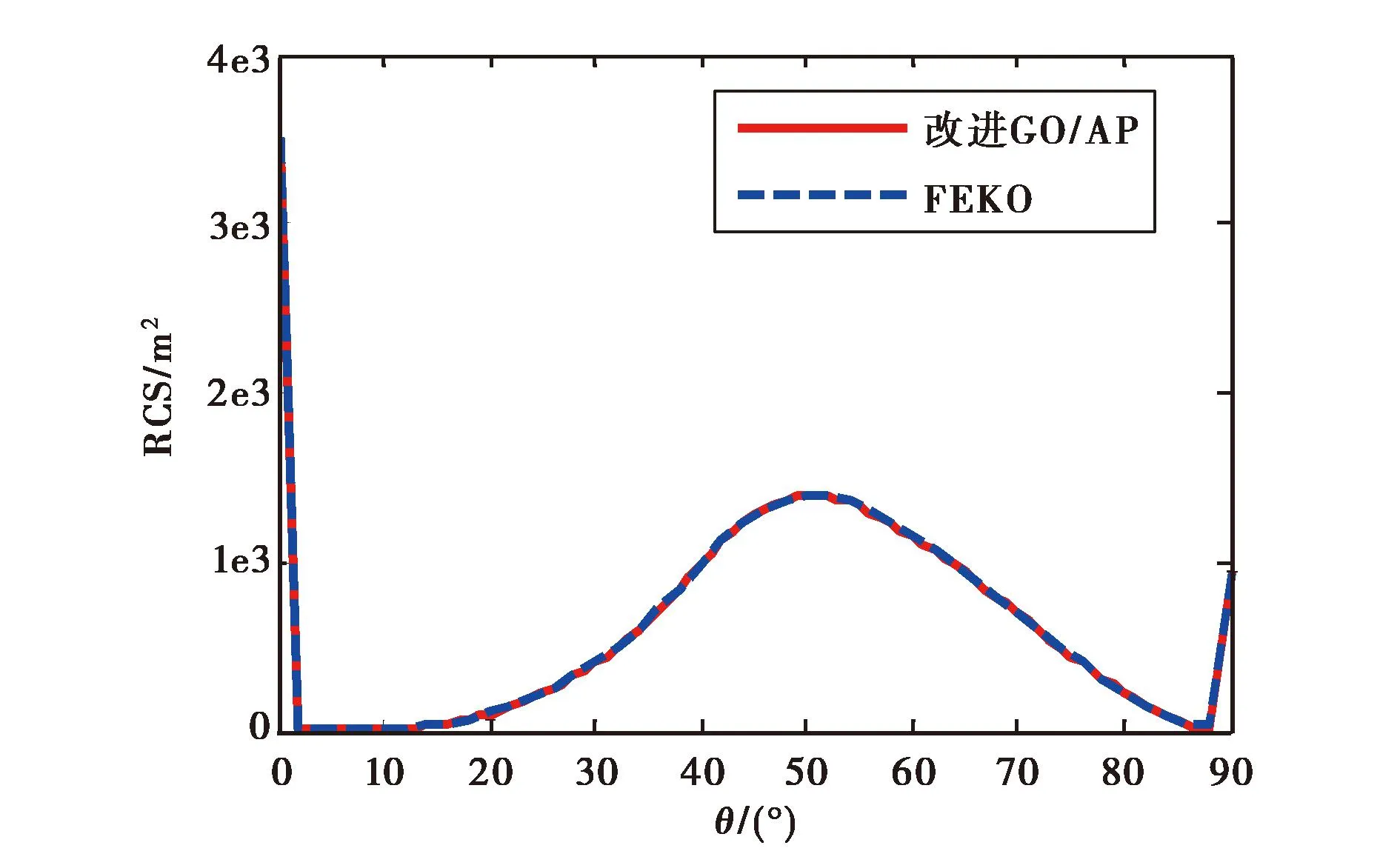
(b) φ=15°∩0°≤θ≤90°时的对比图图7　改进后GO/AP算法与FEKO预估结果对比

4结论

推导建立了利用GO/AP法进行RCS预估的通用流程,按照该流程能够十分方便地计算出不同入射方向下的角反射体RCS的完整表达式;验证了GO/AP法的有效性,说明应用GO/AP法分析三面角反射体的高频散射特性在较大的入射角范围内具有很好的效果,由于算法导出的基础是几何光学和区域投影,应用起来十分简便、高效;通过对边界入射方向的散射分析,利用过峰值的一条直线对GP/AP算法进行改进,提高了GO/AP算法对边界入射方向的适应性.

参考文献

[1]赵维江, 葛德彪. 三面角反射器的高频电磁散射分析[J]. 电波科学学报, 1998, 13(3): 301-303.

ZHAOWJ,GEDB.High-frequencyelectromagneticscatteringbyasquaretrihedralcornerreflector[J].Chinesejournalofradioscience, 1998, 13(3): 301-303. (inChinese)

[2]KEEC,WANGCF.Efficientimplementationofhigh-frequencySBR-POmethodonGPU[J].IEEEantennasandwirelesspropagationletters, 2013, 12(2): 941-944.

[3]LIQ,VERNONRJ.TheoreticalandexperimentalinvestigationofGaussianbeamtransmissionandreflectionbyadielectricslabat110GHz[J].IEEEtransactionsonantennasandpropagation, 2006, 54(11): 3449-3457.

[4] 金亚秋, 刘鹏, 叶红霞, 等. 随机粗糙面与目标复合散射数值模拟理论与方法[M]. 北京: 科学出版社, 2008.

[5]LICF,ZHAOJJ,YINJY.AnalysisofRCSchracteristicofdihedralcornerandtriangulartrihedralcornerreflectors[C]//The5thInternationalConferenceonComputerScience&Education.Hefei,August24-27, 2010.

[6]SHANXJ,YINJY,YUDL,etal.Analysisofartificialcornerreflector’sradarcrosssection:aphysicalopticsperspective[J].Arabianjournalofgeosciences, 2013, 6(8): 2755-2765.

[7]WENGYK,LIS,YANGJL,etal.EfficientsolutiontotheRCSoftrihedralcornerreflector[J].Internationaljournalofappliedelectromagneticsandmechanics, 2015, 47: 533-539.

[8] 黄坦, 徐振海, 戴崇, 等. 隐身目标雷达散射截面最优分布模型选择[J]. 电波科学学报, 2014, 29(5): 899-904.

HUANGT,XUZH,DAIC,etal.OptimaldistributionmodelselectionofstealthtargetRCS[J].Chinesejournalofradioscience, 2014, 29(5): 899-904. (inChinese)

[9] 丁鹭飞, 耿富录. 雷达原理[M]. 西安: 西安电子科技大学出版社, 2002: 130-142.

[10]赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 2012: 207-209.

[11]GROOT J. Cross section computation of trihedral corner reflectors with the geometrical optics approximation[J]. ETT related technologies, 1992, 3(6): 97-102.

[12]RULF B. The effective area of a corner reflector[J]. IEEE antennas and propagation magazine, 1991, 33(2): 48.

[13]张浩斌, 马凯学, 郭陈江, 等. 任意多边形导体板的高频散射分析[J]. 电波科学学报, 2003, 18(1): 53-56.

ZHANG H B, MA K X, GUO C J, et al. High-frequency scattering analysis of arbitrary shape conductor plate[J]. Chinese journal of radio science, 2003, 18(1): 53-56. (in Chinese)

High-frequency method for the evaluation of the radar cross section of corner reflectors

FAN XuemanHU ShengliangHE Jingbo

(ElectronicsEngineeringCollege,NavalUniversityofEngineering,Wuhan430033,China)

AbstractGeometrical optics/area projection(GO/AP) is a hybrid high-frequency method, which can estimate the corner reflector monostatic radar cross section(RCS). The general process of RCS estimation using GO/AP method is proposed, and the complete RCS analytic expressions of triangular trihedral corner reflectors are derived, which are compared with FEKO simulation results as well as empirical formula of maximum value, and the validity of GO/AP method is confirmed. The GO/AP method is improved at boundary angles of incidence further broadening the adaptive range of the GO/AP method.

KeywordsRCS; GO/AP; effective reflection area; corner reflector; FEKO

收稿日期：2015-06-14

中图分类号TN957.52

文献标志码A

文章编号1005-0388(2016)02-0331-06

DOI10.13443/j.cjors.2015061401

作者简介

范学满(1989-),男，山东人,海军工程大学电子工程学院博士研究生,主要研究方向为精确制导与对抗.

胡生亮(1974-),男,安徽人,海军工程大学电子工程学院教授,博士生导师,主要研究方向为无源对抗.

贺静波(1979-),男,河北人,海军工程大学电子工程学院讲师,主要研究方向为随机微分理论及应用.

范学满, 胡生亮, 贺静波. 一种角反射体雷达散射截面积的高频预估算法[J]. 电波科学学报,2016,31(2):331-335+362. DOI: 10.13443/j.cjors.2015061401

FAN X M, HU S L, HE J B. High-frequency method for the evaluation of the radar cross section of corner reflectors[J]. Chinese journal of radio science,2016,31(2):331-335+362. (in Chinese). DOI: 10.13443/j.cjors.2015061401

资助项目: 国家自然科学基金(No.61401493)； 装备预研基金重点项目(No.9140A01010415JB11002)

联系人： 范学满 E-mail: oucfanxm@163.com