基于改进黑洞算法的阵列天线方向图综合

董健　 钱婷婷　施荣华

2.中国科学院电磁空间信息重点实验室,中国科学技术大学，合肥 230027)



基于改进黑洞算法的阵列天线方向图综合

董健1钱婷婷2施荣华1

2.中国科学院电磁空间信息重点实验室,中国科学技术大学，合肥 230027)

摘要提出一种基于改进黑洞算法的阵列天线方向图综合方法,在可控吸收率的基础上实施后向学习机制,增加种群多样性以避免早熟收敛.针对基本黑洞算法在局部搜索方面的不足引入爬山搜索算子,增加个体搜索深度以提高寻优效率.将所提算法应用于稀疏天线阵和等距非均匀天线阵的方向图综合,仿真结果验证了所提算法解决该类问题的有效性.

关键词阵列天线;黑洞算法;方向图综合

引言

阵列天线在移动通信、雷达、遥感等领域具有广泛的应用.方向图综合作为阵列天线的核心技术之一,通过设计阵元位置、电流激励幅值和相位等参数,以实现期望的远区方向图特性,如低旁瓣、深零陷等.实际问题中,传统的方向图综合方法如泰勒-切比雪夫方法因要求目标函数连续可微而使应用受限,需研究新的优化算法.近年来,遗传算法(Genetic Algorithm,GA)[1-3]、蚁群算法(Ant Colony Optimization,ACO)[4-5]、粒子群算法(Particle Swarm Optimization, PSO)[6-8]等一系列智能优化算法以其通用性和全局搜索能力广泛应用于阵列天线综合中.文献[9]采用基于实数编码的遗传算法实现了对稀疏天线阵列的优化;文献[10]提出了基于全局最优粒子微扰和跳变的惯性权重策略的改进型粒子群算法,用于解决早熟收敛问题.针对GA和PSO的收敛速度慢、搜索效率较低等问题,Zhang[11]等人根据黑洞物理现象提出了一种黑洞粒子群算法(Black Hole Particle Swarm Optimization, BHPSO).该算法选取黑洞作为全局最优解,令种群中的其他粒子向黑洞位置靠近;在此过程中粒子会以一定概率进入黑洞,然后以一定概率逃脱黑洞,这些行为有效扩大了搜索区域,加快了收敛速度并防止在迭代过程中陷入局部极值,但是该算法没有解决黑洞边界问题以及多余星体吸收的问题.文献[12]在文献[11]的基础上提出了黑洞 (Black Hole, BH) 算法,通过引入黑洞半径使算法更接近天文学黑洞的真实情形,并具有黑洞现象的一般特性,但是该算法在局部搜索方面仍存在缺陷.

鉴于此,本文在文献[12]的基础上提出一种改进黑洞(Modified Black Hole, MBH)算法,在可控吸收率的基础上实施后向学习机制,增加种群多样性,从而避免算法早熟收敛.针对基本黑洞算法在局部搜索方面的不足引入爬山搜索算子,改善算法的局部搜索能力以提高寻优效率.将改进算法应用于稀疏天线阵和等距非均匀天线阵的方向图综合,仿真结果表明MBH算法得到的天线阵方向图能很好地满足天线设计要求.

1基本的黑洞算法

“黑洞”一词最先于1969年由美国物理学家John Archibald Wheeler命名,它是由恒星“死亡”后发生引力坍缩而产生的.黑洞的质量极其大,体积却非常小,所以它的密度无限大. 黑洞会产生极为强劲的引力场,任何物质和辐射在进入到黑洞的视界范围内就会被吸引进去,再也无法逃逸,就连现在已知的传播速度最快的光也无法挣脱黑洞的引力束缚.

在天文学上,当一个天体的半径低于史瓦西半径时,便会成为黑洞.史瓦西半径的计算公式[12]为

(1)

式中: G是引力常数; M是黑洞质量; c是光速.

黑洞算法主要是模仿天文学上的黑洞现象,通过在整个搜索区域内随机设置一定数量规模的星体,然后以数学方式确定每一个星体的适应度值,选择一个具有最优适应度值的星体作为黑洞.黑洞本身可视为当前全局最优解,而黑洞的视界范围(以R为半径)则视为当前全局最优解所在的位置区域.该算法中的黑洞具有与天文学黑洞一样的强吸引力,搜索区域内的其他星体都将向黑洞靠近并无法逃逸.所有星体向黑洞靠近的公式[12]为

xi(t+1)=xi(t)+rand[0,1]×

(xBH-xi(t))

∀i; i≠best.

(2)

式中: xi(t)是第i个星体在t次迭代时的位置; xi(t+1)是第i个星体在t+1次迭代时的位置; xBH是黑洞位置.

在被黑洞吸引的过程中,如果一个星体的适应度值比黑洞的适应度值更好,说明当前黑洞所在位置并非全局最优,此时需要将当前黑洞所在位置与适应度值更优的星体的位置进行交换,然后以新生成的黑洞为中心,通过位置更新公式(2)使所有其他星体开始向新的黑洞靠近.

在迭代过程中,如果星体进入黑洞的视界范围内,即星体与黑洞的距离小于黑洞半径时,星体将被黑洞吸收.为了保证星体的总数量不变,每当一个星体被黑洞吸收而消亡时,都必须在整个搜索区域内随机设置一个新的星体,以取代之前被黑洞吸收的星体.黑洞半径的计算公式[12]为

(3)

式中: fBH是黑洞的适应度值; fi是第i个星体的适应度值; M是星体的数量.

2基于改进黑洞算法的阵列天线方向图综合

2.1改进的黑洞算法

基本黑洞算法给出了黑洞视界范围的计算公式,当星体进入黑洞视界范围内则被吸收,但是在优化过程中如何衡量星体与黑洞的距离则是需要考虑的问题.由此,本文提出可控吸收率的距离公式,用来确定星体与黑洞之间的距离:

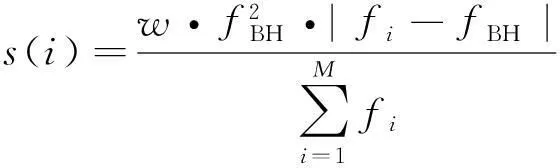
(4)

式中: s(i)是第i个星体与黑洞之间的距离; fi是第i个星体的适应度值; fBH是黑洞的适应度值; M是星体数量; w是吸收率. w控制被黑洞吸收的星体数量,w越小被吸收的星体数量越多,从而随机产生新个体的机会越多;但是w过小又会使算法趋于纯粹的随机搜索,寻优效率降低.在仿真实验中,w的取值一般设为[0.1, 0.5].

根据可控吸收率的距离公式(4)可以获得星体与黑洞的距离,如果该距离小于黑洞半径,则星体被吸收,此时在搜索区域生成随机解取代被吸收的星体,但是这会导致寻优时间随着随机产生的星体位置与黑洞位置的距离远近而发生变化.根据概率学原理,对于每个随机产生的个体以及它的后向解而言,两者各有二分之一的几率远离问题的最优解,若将两者中适应度值较优的个体作为种群成员将在很大程度上提高收敛速度,因此本文引入后向学习机制,当星体与黑洞的距离小于黑洞半径时,实施该机制生成新的个体,从而提高候选解的丰富度.后向学习机制的具体操作过程如下:

1) 对于每个新产生的星体Xi=(xi1,xi2,…,xij,…,xiD),j=1,2,…,D,其中D表示维数,每一维分量均满足

xij∈[xmin,xmax].

(5)

(6)

将此后向学习机制应用于优化过程,每次星体被黑洞吸收后,根据随机产生的星体找出其对应的后向星体,从两者中选择适应度值较优的星体位置作为本次新产生星体的最终位置.后向学习机制的引入有利于增加种群多样性,使得在迭代过程中算法的全局搜索能力得以加强.

基本的黑洞算法相较于粒子群算法只有一个位置更新公式,没有速度更新公式,所以操作简单,控制参数少.但是从位置更新公式(2)可以看出,所有星体均向全局最优解(即黑洞所在位置)移动,所以基本黑洞算法在局部搜索方面存在缺陷,导致寻优效率不足,因此本文引入爬山搜索算子,以增强算法的局部搜索能力.爬山局部搜索的思想是对每一个星体在一定范围内作邻域搜索,在每一个小空间中选择最优的解,以增加个体搜索的深度,有效提高最优解的质量.本文采用的爬山搜索算子利用反馈信息帮助生成解的决策,通过启发式搜索选择个体以避免遍历,从而达到提高效率的目的.

爬山搜索算子所执行的具体操作如下:

1) 对每一个星体Xi=(xi1,xi2,…,xim,…，xin,…,xiD),且m

4) 按上述步骤搜索searchNum次,即完成对星体Xi的邻域搜索.

图1为MBH算法的伪代码.

图1　MBH算法的伪代码

2.2阵列天线方向图综合

阵列天线的方向图综合是指使用优化方法设计天线系统,确定天线阵元位置、相位和电流幅值等参数,使其满足期望的主瓣宽度、旁瓣电平等性能指标.本文主要对稀疏天线阵和等距非均匀天线阵进行优化.

对于一个阵元数为2N的对称直线阵,排列如图2所示,假设每个阵元的相位相同,则阵列天线的远场方向图[4]为

(7)

式中:An是第n个阵元的激励电流幅值;d=λ/2是阵元间距;φ是入射信号相对于阵列轴线的方向角.

图2　阵元数为2N的对称直线阵

对于平面稀疏阵列方向图综合问题,考虑一个对称的2N×2M的矩形二维阵列,排列如图3所示,各个阵元的相位相同,x轴和y轴的阵元间距均为d=λ/2,则这个平面阵的方向图函数[4]为

F(θ,φ)

= 4∑Nn=1∑Mm=1Anmcos(2n-1)·12kd·éëêê

(8)

式中:k=2π/λ;Anm是第(n,m)个阵元的激励电流幅值.

图3　2N×2M的对称矩形平面阵

本文的目标函数由下式给出:

(9)

(10)

f=a·fPSL+b·fNULL+c·DNULL_ST.

(11)

式中:LPS和LSL分别是实际峰值旁瓣电平和目标旁瓣电平； 而LNUL和LNUL,d分别是平均零陷深度和设计零陷深度;DNULL_ST表示方向图零陷深度的方差;a、b、c分别是各项指标的权值.

3仿真结果及分析

实例1稀疏直线阵方向图综合

(a) η=80%

(b) η=78%图4　不同填充率下的阵列方向图

条件下的阵列方向图.主要参数设置如下:阵元数为2N=100,种群规模starsize=50,最大迭代次数eranum=200,局部搜索次数searchNum=3,吸收率w=0.3.

表1给出了MBH算法、BA算法[13]和GA算法[9]在一定条件下对稀疏直线阵优化结果的比较.

当填充率η=80%,阵元数2N=100时,文献[13]中BA的总计算次数为40 000次(蜂群规模200,迭代次数200),得到的旁瓣电平为-20.79dB,MBH算法的总计算次数为10 000次(星体规模50,迭代次数200),其峰值旁瓣电平为-21.14dB,而两种算法得到的3dB波瓣宽度基本一致,说明MBH算法的搜索能力更强,寻优效果更好.当填充率η=78%,阵元数2N=100时,文献[9]中GA的总计算次数为60 000次(种群规模200,迭代次数300),得到的旁瓣电平为-20.56dB,MBH算法仍然采用50个星体进行200次迭代,得到的旁瓣电平为-20.86dB,而两者的3dB波瓣宽度基本一致,显然,MBH算法的寻优效率更高,而且计算代价更小.

表1　MBH、BA[13]和GA[9]对稀疏

为说明吸收率w对改进黑洞算法收敛性能的影响,图5给出了w取值不同时收敛曲线的变化情况,其中填充率η=77%,阵元数2N=200,种群规模starsize=50,迭代次数eranum=150.由图5可以看出,w过大或过小均会影响寻优效率,而当w取适当值(如w=0.3)时改进算法具有较好的收敛性能.

图5　w取值不同时收敛曲线的变化情况

猫群搜索算子是猫群算法[14]中的局部搜索策略,图6给出了未进行局部搜索、采用爬山搜索算子和采用猫群搜索算子的收敛曲线,其中填充率η=77%,阵元数2N=200,种群规模starsize=50,迭代次数eranum=150.由图6可以看出,采用爬山搜索算子的改进黑洞算法在70代以后开始收敛,而且收敛速度更快,寻优效果更好.

图6　未进行局部搜索以及采用不同局部搜索策略的收敛曲线

实例2稀疏平面阵方向图综合

考虑一个20×20的对称矩形稀疏平面阵列,采用MBH算法对其旁瓣电平进行优化.阵元位置按填充率η=55%选取,考虑对称,只需要对其中的四分之一阵元位置分布进行优化,各阵元激励幅度取值为0或1(其中1表示该位置有阵元,0表示该位置无阵元),适应度函数为式(11),取a=1,b=c=0.其他参数分别为:starsize=50,eranum=200,searchNum=3,w=0.3.图7给出了优化后的阵元位置分布情况以及优化得到的φ=0°和φ=90°的阵列方向图.

表2给出了MBH算法和PSO[15]在相同条件下对稀疏平面阵优化结果的比较.由表2可以看出,MBH算法在两个方向得到的峰值旁瓣电平均比文献[15]的结果低,说明MBH算法的寻优效果更好,搜索能力更强.

(a) 优化后的阵元位置分布

(b) 优化后的阵列方向图图7　优化后的阵元位置分布和阵列方向图

实例3等距非均匀直线阵方向图综合

表2MBH和PSO[15]对稀疏平面阵优化结果的比较

填充率/%阵元数使用的算法ϕ=0°的LPS/dBϕ=90°的LPS/dB5520×20MBH-25.93-30.185520×20PSO[15]-25.24-25.16

等距非均匀直线阵是指阵元间距相等,激励电流非均匀的直线阵.考虑2N=20个天线阵元,激励电流相位相同,幅值对称分布,采用MBH算法对电流幅值进行优化,适应度函数选择式(11).设计指标为LSL=-40 dB,零功率波瓣宽度2θ0=20°,要求主瓣对准90°方向,LNUL,d=-90 dB,电流幅值的优化范围为[0,1],要求阵列方向图在φ=64°、 70°、 76°三个方向形成深零陷.其他参数分别为starsize=50,eranum=200,searchNum=3,w=0.3,参考文献[16],取a=0.8,b=0.2,c=1.0.

优化结果如下,激励电流幅值依次为:0.896 83,0.868 40,0.806 64,0.688 26,0.576 19,0.490 81,0.358 56,0.244 22,0.135 14,0.102 26.计算得到的阵列方向图如图8所示.

图8　在φ=64°、 70°、 76°三个方向形成零陷的阵列方向图

表3给出了MBH算法、量子粒子群算法(Qua-ntum Particle Swarm Optimization, QPSO)[16]和GA算法[17]在设计指标相同的情况下对20个阵元的等距非均匀直线阵优化结果的比较.

由表3可以看出,虽然文献[16]中QPSO算法得到的峰值旁瓣电平比MBH算法的峰值旁瓣电平低,但其零功率波瓣宽度比MBH算法得到的结果展宽了1.4°,说明文献[16]是通过牺牲主瓣宽度才得以降低旁瓣电平的,而且MBH算法得到的三个角度的零陷深度均低于文献[16]的零陷深度,综合比较各项参数,说明MBH算法的寻优效果更好.文献[17]中GA得到的峰值旁瓣电平比MBH算法的峰值旁瓣电平高1.71 dB,而两种算法得到的零功率波瓣宽度相差不多,MBH算法在64°、70°和76°三个方向的零陷深度均远远低于文献[17],综合考虑各项参数,说明MBH算法的搜索能力更强,寻优效果更好.

表3　MBH、QPSO[16]和GA[17]对等距非

4结论

黑洞算法作为近几年提出的随机优化方法,为多维非线性、不可微的复杂优化问题的求解提供了一种新的思路和解决方法.基本黑洞算法操作简单,控制参数少,但在局部搜索方面存在缺陷,寻优效率不高.本文提出一种改进的黑洞算法,在可控吸收率的基础上实施后向学习机制,有利于增加种群多样性,使得在迭代过程中算法的全局搜索能力得以加强,从而避免算法早熟收敛.同时针对基本黑洞算法在局部搜索方面的不足,引入了爬山搜索算子,改善算法的局部搜索能力,提高寻优效率.将该算法应用于阵列天线方向图综合,具有收敛速度快、旁瓣电平低、零陷深等优势,充分体现了其解决多维复杂问题的能力.

参考文献

[1] MAHANTI G K, DAS S, CHAKRABORTY A. Design of phase-differentiated reconfigurable array antennas with minimum dynamic range ratio[J]. IEEE antennas and wireless propagation letters, 2006, 5(2): 262-264.

[2] ELKAMCHOUCHI H M, HASSAN M M. Array pattern synthesis approach using a genetic algorithm[J]. IET microwave antennas propagation, 2014, 8(4): 1236-1240.

[3] ZENG G Q, LI S Y, ZHANG Y, et al. Low side lobe pattern synthesis using projection method with genetic algorithm for truncated cone conformal phased arrays[J]. Journal of systems engineering and electronics, 2014, 25(4): 554-559.

[4] QUEVEDO-TERUEL O, RAJO-IGLESIAS E. Ant colony optimization in thinned array synthesis with minimum sidelobe level[J]. IEEE antennas and wireless propagation letters, 2006, 5(3): 349-352.

[5] LASEETHA T S J, SUKANESH R. Investigations on the synthesis of uniform linear antenna array using biogeography-based optimisation techniques[J]. International journal of bio-inspired computation, 2012, 4(2): 119-130.

[6] GIES D, RAHMAT-SAMMI Y. Particle swarm optimization for reconfigurable phase-differentiated array design[J]. Microwave and optical technology letters, 2003, 38(3): 168-175.

[7] CHATTERJEE S, CHATTERJEE S, PODDAR D R. Synthesis of linear array using Taylor distribution and particle swarm optimisation [J]. International journal of electronics, 2015, 102(3): 514-528.

[8] HE G L, WU B. Unified particle swarm optimization with random ternary variables and its application to antenna array synthesis[J]. Journal of electromagnetic waves and applications, 2014, 28(6): 752-764.

[9] MAHANTI G K, PATHAK N, MAHANTI P. Synthesis of thinned linear antenna arrays with fixed sidelobe level using real-coded genetic algorithm[J]. Progress in electromagentics research, 2007, 75(2): 319-328.

[10]金荣洪, 袁智皓, 耿军平, 等. 基于改进粒子群算法的天线方向图综合技术[J]. 电波科学学报, 2006, 21(6): 873-878.

JIN R H, YUAN Z H, GENG J P, et al. The pattern synthesis of antennas based on a modified PSO algorithm[J]. Chinese journal of radio science, 2006, 21(6): 873-878. (in Chinese)

[11]ZHANG J, LIU K, TAN Y, et al. Random black hole particle swarm optimization and its application[C]//IEEE International Conference on Neural Networks and Signal Processing. Zhengjiang, 2008: 359-365.

[12]HATAMLOUS A. Black hole: a new heuristic optimization approach for data clustering[J]. Information science, 2013, 222(4): 175-184.

[13]GUNEY K, ONAY M. Synthesis of thinned linear antenna arrays using bees algorithm[J]. Microwave and optical technology letters, 2011, 53(4): 795-799.

[14]杨淑莹, 张桦. 群体智能与仿生计算——MATLAB技术实现[M]. 北京: 电子工业出版社, 2012.

[15]袁智皓, 耿军平, 金荣洪, 等. 基于改进的粒子群算法的二维阵列天线方向图综合技术[J]. 电子与信息学报, 2007, 29(5): 1236-1239.

YUAN Z H, GENG J P, JIN R H, et al. Pattern synthesis of 2-D arrays based on a modified particle swarm optimization algorithm[J]. Journal of electronics & information technology, 2007, 29(5): 1236-1239. (in Chinese)

[16]李金金, 田雨波. 基于量子粒子群改进算法的直线阵综合[J]. 电波科学学报, 2012, 27(2): 255-259.

LI J J, TIAN Y B. Pattern synthesis of linear antenna array based on improved quantum particle swarm optimization[J]. Chinese journal of radio science, 2012, 27(2): 255-259. (in Chinese)

[17]马云辉. 阵列天线的遗传算法综合[J]. 电波科学学报, 2001, 16(2): 172-176.

MA Y H. Synthesis of the array antenna using genetic algorithm[J]. Chinese journal of radio science, 2001, 16(2): 172-176. (in Chinese)

Pattern synthesis of antenna array based on a modified black hole algorithm

DONG Jian1QIAN Tingting2SHI Ronghua1

(1.SchoolofInformationScienceandEngineering,CentralSouthUniversity,Changsha410075,China;2.KeyLaboratoryofElectromagneticSpaceInformationofChineseAcademyofScience，UniversityofScienceandTechnologyofChina,Hefei230027,China)

AbstractA modified black hole(MBH) algorithm is proposed for pattern synthesis of antenna array. Based on controllable absorptivity, backward learning mechanism is adopted to enrich the diversity of the population so as to effectively avoid premature. Also, a climbing search operator is introduced to enhance the local search capability and increase the search depth of the individual and hence improve the optimization efficiency. The proposed MBH algorithm is applied to the pattern synthesis of thinned arrays and equidistant non-uniform arrays. The simulation results validate the effectiveness of the proposed algorithm in solving array pattern synthesis problems.

Keywordsantenna array; black hole algorithm; pattern synthesis

收稿日期：2015-06-23

中图分类号TN820.1

文献标志码A

文章编号1005-0388(2016)02-0236-07

DOI10.13443/j.cjors.2015062302

作者简介

董健(1980-),男,湖南人,副教授,研究方向为天线理论与技术、微波遥感、阵列信号处理等.

钱婷婷(1992-),女,安徽人,硕士研究生,研究方向为微波毫米波成像技术.

施荣华(1963-),男,湖南人,教授,研究方向为无线通信、智能计算与信息处理等.

董健, 钱婷婷, 施荣华. 基于改进黑洞算法的阵列天线方向图综合[J]. 电波科学学报,2016,31(2):236-242+261. DOI:10.13443/j.cjors.2015062302

DONG J， QIAN T T， SHI R H. Pattern synthesis of antenna array based on a modified black hole algorithm [J]. Chinese journal of radio science,2016,31(2):236-242+261. (in Chinese). DOI:10.13443/j.cjors.2015062302

资助项目: 国家自然科学基金(61201086); 教育部博士学科点专项科研基金(20110162120044); 湖南省科技计划项目(2014GK3022); 广东省科技计划项目(2013B090500007)； 东莞市产学研合作项目(2014509102205)

联系人： 董健 E-mail:dong0531@126.com