溶瘤疗法动力学模型的改进与分析
2016-06-22苏永美
陈 影,苏永美
(北京科技大学 数理学院,北京 100083)
溶瘤疗法动力学模型的改进与分析
陈影,苏永美
(北京科技大学 数理学院,北京 100083)
摘要:研究了一个改进的溶瘤疗法动力学模型。通过分析该模型,得到了解的有界性和非负性。利用微分方程理论分析了零平衡点的不稳定性、边界平衡点的全局稳定性及正平衡点的局部稳定性。最后,通过数值模拟来验证边界平衡点和正平衡点的稳定性。
关键词:肿瘤;溶瘤疗法;稳定性;数值模拟
0引言
肿瘤是严重威胁人类健康的疾病,传统的放疗和化疗在杀死肿瘤细胞的同时,对人体正常细胞也会造成伤害[1]。溶瘤病毒是一类具有复制能力的肿瘤杀伤型病毒,无法在正常的机体细胞内复制,因此,对于正常的细胞无杀伤作用[2]。
许多学者对溶瘤疗法做了深入研究[3-5],而且溶瘤疗法也被广泛地应用到临床治疗[6-8]方面。近年来,为了更好地研究肿瘤病毒疗法的动力学模型,并且找到更好的治疗策略,一些相关的数学模型被提出[9-15]。文献[2]提出了一般模型,这个模型中不包含病毒这个变量。第一个关于溶瘤疗法的微分方程数学模型是由文献[11]提出的。事实上,病毒数量的变化对溶瘤疗法的动力学研究也非常重要。文献[16]建立了同时包含肿瘤细胞和溶瘤病毒两个变量的数学模型,并对肿瘤病毒用到了Logistic增长。文献[9]在数学模型中加入了病毒释放率b,即一个感染的肿瘤细胞在裂解时所产生的病毒数量。文献[9]提出的病毒疗法一般模型为:
(1)

(2)

模型(2)的初始条件满足如下形式:
x(0)>0,y(0)>0,v(0)>0。
(3)
1解的有界性和非负性
性质1模型(2)满足初始条件(3)的解,对所有的t>0都是最终有界的,并且是正的。
下面证明模型(2)满足初始条件(3)的解都是最终有界的。
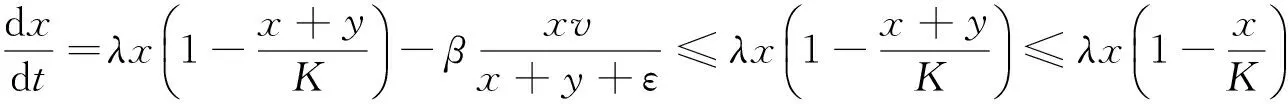
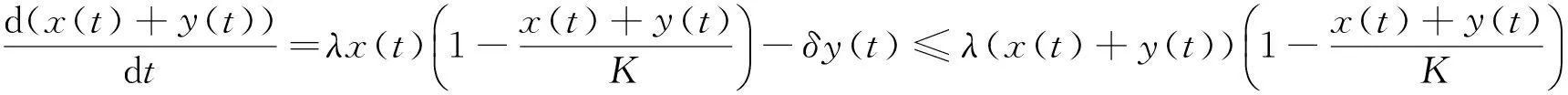

由上面分析可得出:满足条件(3)的模型(2)的解,对所有的t>0是正的,并且是最终有界的。
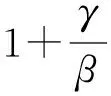




2稳定性分析

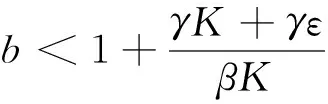

μ1=-λ;
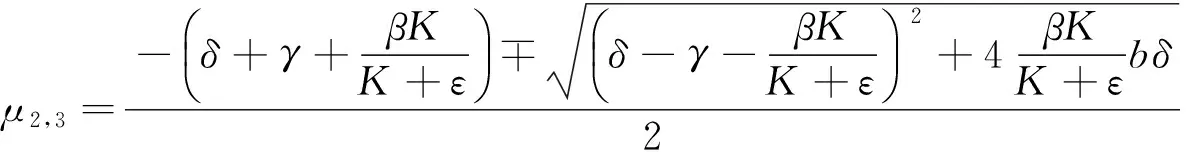
对于一切非负参数,μ1和μ2都是负的。
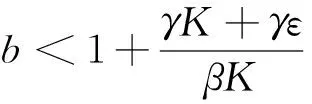




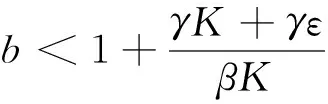





特征方程为:
p(μ)=μ3+Aμ2+Bμ+C,
(4)
其中:A=-a11-a22-a33;B=a11a22+a22a33+a11a33-a12a21-a13a31-a23a32;C=a11a23a32+a12a21a33+a13a22a31-a11a22a33-a12a23a31-a13a21a31。

(5)
由Routh-Hurwitz原理,当式(5)满足时,方程(4)的所有根都有负实部。
定理3 当条件(5)满足时,平衡点E*是局部渐进稳定的。
3数值模拟
用MATLAB模拟平衡点的稳定性,选取参数:λ=0.5,K=9×106,β=0.2,γ=0.6,δ=0.8,b=2,ε=0.009,此时定理1的条件满足,平衡点E1的稳定性模拟结果如图1所示。选取b=5,其他参数不变,此时定理3的条件满足,且平衡点E*存在,其稳定性模拟结果如图2所示。

图1b=2时,E1的稳定性模拟 图2b=5时,E*的稳定性模拟
4结论

参考文献:
[1]ZHOU L,HE W W,ZHU Z N,et al.The clinical research progress for oncolytic adenovirus targeting cancer therapy[J].China biotechnology,2013,33(12):105-113.
[2]KOMAROVA N L,WODARD D.ODE models for oncolytic virus dynamics[J].Journal of theoretical biology,2010,263(4):530-543.
[3]EAGER R M,NEMUNAITIS J.Clinical development directions in oncolytic viral therapy[J].Cancer gene therapy,2011,18(5):305-317.
[4]DONNELLY O G,ERRING M F,PRESTWICH R,et al.Recent clinical experience with oncolytic viruses[J].Current gharmaceutical biotechnology,2012,13(9):1834-1841.
[5]RUSSELL S J,PENG K W,BELL J C.Oncolytic virotherapy[J].Nature biotechnology,2012,30(7):658-670.
[6]MIEST T S,CATTANEO R.New viruses for cancer therapy:meeting clinical needs[J].Nature reviews microbiology,2014,12(1):23-34.
[7]PATEL M R,KRATZKE R A.Oncolytic virus therapy for cancer:the first wave of translational clinical trials[J].Translational research,2013,161(4):355-364.
[8]AGHI M,MARTUZA R L.Oncolytic viral therapies-the clinical experience[J].Oncogene,2005,24(52):7802-7816.
[9]TIAN J P.The replicability of oncolytic virus:defining conditions in tumor virotherapy[J].Mathematical biosciences and engineering,2011,8(3):841-860.
[10]SI W,ZHANG W N.Control exponential growth of tumor cells with slow spread of oncolytic virus[J].Journal of theoretical biology,2015,367:111-129.
[11]WODARZ D.Viruses as antitumor weapons:defining conditions for tumor remission[J].Cancer research,2001,61(8):3501-3507.
[12]CHOUDHURY B S,NASIPURI B.Efficient virotherapy of cancer in the presence of immune response[J].International journal of dynamics and control,2014,2(3):314-325.
[13]BAJZER Z,CARR T,JOSIC K,et al.Modeling of cancer virotherapy with recombinant measles viruses[J].Theoretical biology,2008,252(1):109-122.
[14]NOVOZHILOV A S,BEREZOVSKAYA F S,KOONIN E V,et al.Mathematical modeling of tumor therapy with oncolytic viruses:regimes with complete tumor elimination within the framework of deterministic models[J].Biology direct,2006,1(6):1-18.
[15]WANG Y J,TIAN J P,WEI J J.Lytic cycle:a defining process in oncolytic virotherapy[J].Applied mathematical modeling,2013,37(8):5962-5978.
[16]WODARZ D.Gene therapy for killing p53-negative cancer cells:use of replicating versus nonreplicating agents[J].Human gene therapy,2013,14(2):153-159.
基金项目:国家自然科学基金项目(61074192,11101028);国家中医临床研究基地业务建设科研基金项目(JDZX2015299)
作者简介:陈影(1990-),女,河南驻马店人,硕士生;苏永美(1971-),女,山东临沂人,副教授,博士,硕士生导师,主要从事常微分定性和稳定性分析、生物数学模型及微分方程模型的最优控制等方面的研究.
收稿日期:2015-12-23
文章编号:1672-6871(2016)04-0092-05
DOI:10.15926/j.cnki.issn1672-6871.2016.04.019
中图分类号:O175.13
文献标志码:A
