POT模型的车辆荷载极值预测及荷载效应
2016-06-22袁伟璋黄海云张俊平刘泽戈
袁伟璋,黄海云,张俊平,2,尹 兴,刘泽戈
(1.广州大学 土木工程学院,广东 广州 510006;2.广东交通职业技术学院,广东 广州 510170)
POT模型的车辆荷载极值预测及荷载效应
袁伟璋1,黄海云1,张俊平1,2,尹兴1,刘泽戈1
(1.广州大学 土木工程学院,广东 广州 510006;2.广东交通职业技术学院,广东 广州 510170)
摘要:为了研究车辆荷载的发展变异对桥梁结构的影响,根据渝湛高速公路176 918辆六轴车的动态称重系统实测数据,采用基于极值理论的超越阈值模型预测未来5~20年可能出现的车辆荷载极值,并加载于某典型桥梁进行荷载效应分析。分析结果表明:本文预测的基准期为20年的车辆荷载极值,对1#空心板所产生的弯矩比JTG D60—2015的车辆荷载和挂120大2.40倍和0.47倍。车辆荷载的发展变异能够直接影响现行桥梁结构的安全运营。
关键词:超越阈值模型;总质量;轴质量;车辆荷载效应
0引言
近20年,中国运营的车辆荷载发展较快,超载超限运输车辆日益增多,对既有桥梁结构安全构成了严重威胁。在预测最大车辆荷载时,一般采用常用的分布类型对实测荷载样本进行拟合,取基准期内的某极值分位数作为评估参考值。这些方法虽然可以较好地描述数据的整体分布,但难以描述数据的尾部,而分布的尾部才能够反映问题的核心[1]。文献[2]用威布尔分布和对数正态分布作为底分布函数,分别拟合出某道路的车辆荷载模型,再取某分位数作为荷载极值。文献[3]根据动态称重系统(weigh-in-motion system,WIM)实测数据,通过Rice公式推算出不同重现期不同跨径桥梁结构的车辆荷载效应。文献[4-5]利用渐进极值理论,对不同交通状态下的车辆荷载效应进行了极值预测。文献[6]指出经典极值理论的问题是实际中很难找出完全描述样本特性的底分布,而利用Rice公式进行外推,样本数据本身必须符合高斯平稳过程,同时存在拟合起点和区间难以选择的问题。利用渐进极值理论进行极值外推虽然有较高的精度和效率,但需要较大的数据样本,当样本量较小时,存在精度低的问题。超越阈值(peak over threshold,POT)模型是基于渐进极值理论的一种极值预测方法,依赖尾部的数据,得出的结果更加客观,避免了假设检验方法构建模型的主观性。同时,文献[7-9]研究发现:小跨径桥梁活载与恒载的比值较大,故其受到车辆荷载变异的影响尤为显著。
文献[10]统计了京珠高速公路某出口2012年4月的80 169辆车,其中,六轴车总数量达20 991辆,占总车流的26.2%,超载率高达70.5%。六轴车不仅数量比较多,而且超载问题也十分严重,中小跨径桥梁汽车荷载效应值往往由它来控制。渝湛高速公路(国道编号G050)连接重庆市和广东省湛江市,是中国主干道计划纵向干线公路之一,担负着珠三角地区巨量货物的运输需求,交通非常繁忙,其实际交通流状况对中国其他后工业化地区具有很强的借鉴意义。因此,本文选取渝湛高速某出口在2013年共计176 918辆六轴车的动态称重数据,采用POT模型对车辆荷载样本进行拟合,从而预测未来5~20 年可能出现的最大车辆荷载。并采用最小二乘法求得各轴质量占总质量的比例,提取出基准期内最大质量车的车辆荷载,并加载于跨径为16 m的某典型桥梁进行荷载效应分析。
1POT模型及车辆荷载的预测
1.1POT模型
选取渝湛高速某出口在2013年共计176 918辆六轴车的动态称重数据,作为POT模型的样本数据。
假设X1,X2,…,Xn为独立同分布随机变量序列{Xi},并假设独立同分布随机变量序列{Xi}的任意分布函数为F(x)。定义Fμ(y)为随机变量超过阈值μ的条件分布函数,可表示为[1,11]:

(1)
则
F(x)=Fμ(y)(1-F(μ))+F(μ)。
(2)
设X1,X2,…,Xn是来自同分布F(x)总体的样本且满足极值理论[12-14],当有足够大的μ时,随机变量X的分布函数能满足:

(3)
则称X服从广义帕累托分布(general Pareto distribution,GPD)。广义帕累托分布是一种基于极值理论,用于拟合极值样本中尾部数据的分布。当随机变量X足够大时,其高尾部分的条件分布可以用GPD来表示。其中,μ∈R是位置函数,σ>0是尺度参数,ξ∈R是形状参数。
若存在常数an和bn,使得当趋近F(x)的上端点时,Fμ(an+bn)有连续的极限分布,则极限分布定理为:
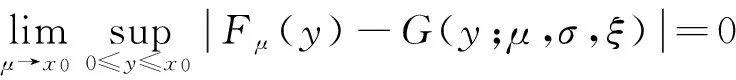
(4)
该定理说明:对于充分大的阈值μ,多数未知分布函数F(x)的超出量分布函数Fμ(y)可用G (y;μ,σ,ξ)近似,即为Fμ(y)≈G (y;μ,σ,ξ),将式(4)代入式(2)可得:
F(x)=G(y;μ,σ,ξ)(1-F(μ))+F(μ)。
(5)
当μ确定以后,可以得到{Xi}中比阈值μ大的个数Nμ。根据式(5),用频率(1-Nμ/n)代替F(μ)的值,可以得到F(x)的表达式为:

(6)

(7)
1.2阈值选取
阈值μ选取的方法主要有图解法和计算法两大类。图解法是根据平均超出量函数e(μ)的线性变化或判断阈值μ改变所引起的参数估计量变化来进行阈值的选取。计算法主要有Hill法和峰度法等。虽然图解法应用较为广泛,但其存在较强的主观性,因此,本文采用峰度法[13-14]进行阈值选取,计算步骤如下:
(Ⅰ)计算样本峰度Kn:

(8)

(Ⅲ)重复第(Ⅰ)步和第(Ⅱ)步,直到峰度小于3为止。
(Ⅳ)在留下来的样本点中选取最大的Xi,此值即为阈值。
该模型使用样本数据,通过峰度法计算,获得阈值μ为71.2t。其中,大于阈值的车辆荷载数目为5 404个,则Nμ/n为3.055%。
1.3参数估计
参数估计是基于现有的车辆荷载数据估计POT模型的未知参数,主要有极大似然估计、矩估计和Bayes估计等方法[15]。经对比分析,选取极大似然法进行参数估计。假定观测到车辆荷载样本序列X1,X2,…,Xn,用极大似然估计方法对参数σ和ξ进行假设推断。由式(3)两边求导可以得到GPD的密度函数为:

(9)
对式(9)两边求自然对数可得GPD的对数极大似然估计函数为:
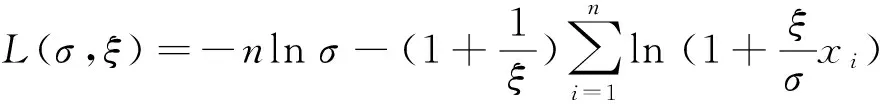
(10)
分别对σ和ξ求偏导,并令其等于0,得:
(11)
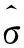

图1 六轴车总质量的尾部分布图
1.4车辆荷载极值预测
绘制六轴车总质量的尾部分布图,如图1所示。由图1可见:GPD尾部分布的实测值与拟合结果符合较好。
把参数估计结果代入POT模型,计算得车辆荷载截口分布为:
基准期T内车辆荷载最大值分布为:FT(X)=[F(X)]T(T为基准期六轴车的车流量)。x的分位数满足:FT(X)=0.95。车辆总质量最大值如表1所示。

表1 应用POT模型估计的车辆总质量最大值

图2 159型车的轴距
加载所使用的车辆荷载采用六轴车中的代表车型159型[16],其轴距见图2。其单轴质量占总车质量的比例关系采用最小二乘法求得。采用表1中基准期为20年的预测总车质量,即178.1 t。单轴质量占总车质量的比例关系和轴质量计算结果见表2。

表2 单轴质量占总车质量的比例关系和轴质量计算结果
2典型桥梁荷载效应计算结果及分析
被加载的桥梁结构采用跨径为16 m的江门某简支梁桥右幅,混凝土标号为C50,设计荷载为公路Ⅰ级,由20条宽1.24 m的空心板底板拼装组成,空心板底板间有1 cm的现浇距离,其横截面图见图3。
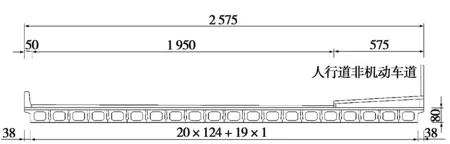
图3 右幅跨中截面图(单位:cm)
本文采用梁格法计算车辆荷载效应,车辆荷载加载的横向位置为靠近中央分隔带防撞栏的0.5 m处,车辆荷载加载的纵向位置与第五轴和跨中中心线重合。同时,把《公路桥涵设计通用规范》JTG D60—2015[17]的车辆荷载和挂120也加载于本模型,最终计算结果见表3。

表3 车辆荷载效应计算结果 N·m
注:1#、2#、3#空心板为图3从左往右数起的前3条空心板;L为桥梁跨径长度。
表1~表3结果表明:(Ⅰ)本文预测的20年基准期的最大车质量达到178.1 t,轴质量达到39.2 t,与JTG D60—2015中所采用的标准车辆荷载相比,车质量增加了223.8%,轴质量增加了180%;与挂120相比,总质量与轴质量分别超出48.4%和30.6%。随着时间的推移,变异还将进一步扩大,对既有道路桥梁的安全运营构成了严重的威胁。(Ⅱ)1#空心板的弯矩达到7.83E+05 N·m,比JTG D60—2015的车辆荷载和挂120产生的弯矩大2.40倍和0.47倍,若使用JTG D60—2015规范桥梁会使桥梁正常安全运营存在隐患,应加强对超载车辆的管理。
3结论
(1)未来20年最大车质量达到178.1 t,轴质量达到39.2 t,其荷载效应1#空心板的弯矩达到7.83E+05 N·m,比JTG D60—2015的车辆荷载和挂120产生的弯矩大2.40倍和0.47倍,总质量和轴质量还会有较大增长,而且直接影响现行桥梁结构的安全运营。
(2)本文预测的最大车辆荷载及其效应以及统计结果,对桥梁设计、安全评估、寿命预测及养护维修都具有重要的参考意义。
参考文献:
[1]CASTILLO E,HADI A S.Fitting the generalized pareto distribution to data[J].Journal of the American statistical association,1997,92(440):1609-1620.
[2]“公路桥梁车辆荷载研究”课题组.公路桥梁车辆荷载研究[J].公路,1997(3):8-12.
[3]杨琪,黄建跃,阮欣,等.基于 WIM数据的桥梁实际汽车荷载效应的研究[J].公路工程,2010,35(4):1-5.
[4]O’BRIEN E J,HAJIALIZADEH D,SHEILS E,et al.Estimation of lifetime maximum distributions of bridge traffic load effects[C]//Proceedings of the 6th International IABMAS Conference.Stresa:Taylor & Francis,2012:1482-1488.
[5]O’CONNOR A,O’BRIEN E J.Traffic load modeling and factors influencing the accuracy of predicted extremes[J].Canadian journal of civil engineering,2005,32(1):270-278.
[6]阮欣,周军勇,石雪飞.桥梁汽车荷载响应的极值外推方法综述[J].同济大学学报(自然科学版),2015,43(9):1339-1346.
[7]张亚平,张起森,李学文.珠江三角洲地区公路交通组成与速度特性研究[J].中南公路工程,2000,25(2):79-81.
[8]许肇峰,王强,刘仰韶.基于 WIM 的广东省公路桥梁车辆荷载模型研究[J].桥梁建设,2012,42(6):39-44.
[9]夏叶飞,李峰峰,顾煜,等.基于 WIM 系统的高速公路桥梁车辆疲劳荷载谱研究[J].公路交通科技,2014,31(3):56-64.
[10]周灿.计重收费模式下运营车辆荷载特征的分析及其发展变异的预测[D].广州:广州大学,2014:54-58.
[11]韩大建.极值分析方法在车辆荷载评估中的应用与比较[J].建筑与科学工程学报,2011,28(2):11-13.
[12]STUART C.An introduction to statistical modeling of extreme values[M].Great Britain:Springer-Verlag London Limited,2001.
[13]陈红英.POT模型在巨灾保险中的应用[D].上海:上海交通大学,2010.
[14]史道济.实用极值统计方法[M].天津:天津科学技术出版社,2005.
[15]高娟.极值分布参数估计方法的研究[D].北京:华北电力大学,2008.
[16]周永涛,鲍卫刚,翟辉,等.我国高速公路交通荷载标准研究[J].公路交通科技,2010,27(2):36-41.
[17]中华人民共和国交通运输部.公路桥涵设计通用规范:JTG D60—2015[S].北京:人民交通出版社,2015.
基金项目:国家自然科学基金项目(51278134);教育部博士点基金项目(20114410110003);广东省交通运输厅科技基金项目(201402022)
作者简介:袁伟璋(1991-),男,广东中山人,硕士生;张俊平(1968-),男,甘肃天水人,教授,博士,博士生导师,主要研究方向为桥梁结构性能评估.
收稿日期:2016-03-24
文章编号:1672-6871(2016)04-0036-05
DOI:10.15926/j.cnki.issn1672-6871.2016.04.008
中图分类号:U441+.2
文献标志码:A
