一种改进的T-S模糊模型建模及优化方法

刘　骏,　殷晓明,　顾幸生

(华东理工大学化工过程先进控制与优化技术教育部重点实验室,上海 200237)

一种改进的T-S模糊模型建模及优化方法

刘骏,殷晓明,顾幸生

(华东理工大学化工过程先进控制与优化技术教育部重点实验室,上海 200237)

摘要：模糊建模是一种有效的非线性系统建模方法,因为非线性系统的复杂性,仍有很多问题难以处理。针对T-S模糊模型,提出了一种改进的建模及优化方法。首先,将快速搜索密度峰聚类和模糊C均值聚类(FCM)算法相结合,使用快速搜索密度峰聚类算法找到聚类个数和初始聚类中心后,再用FCM算法进行聚类;然后,通过最小二乘法辨识结论参数得到初始T-S模糊模型,使用改进的差分进化(DE)算法整体优化模型的结构和参数,获得最终的T-S模型;最后,选择代表性实例,使用MATLAB程序进行仿真分析和比较,验证了本文方法能有效提高T-S模糊模型的辨识精度和速度。

关键词：模糊建模; T-S模型; 模糊C均值聚类; 快速搜索密度峰聚类; 差分进化算法

对复杂工业过程来说,实际对象往往有很强的非线性和不确定性,建立对象的精确数学模型十分困难。即便得出数学模型,因为模型通常十分复杂,很难利用传统控制方法获得需要的控制效果。随着人工智能的发展,许多研究者将智能技术运用到非线性系统建模中,譬如模糊建模、神经网络建模、基于遗传算法建模等,其中模糊建模是一种有效的非线性建模方法。模糊模型本质上是一种非线性模型,拥有优秀的逼近能力,文献[1]已经证明了其能够以任意精度逼近有界闭集上的连续函数。

通过模糊建模方法已经得到了许多经典方法难于描述的复杂非线性系统模型,由于系统的复杂性,依然有许多难以处理的对象。文献[2]通过模糊C均值聚类(Fuzzy C-Means,FCM)获得模型的前件结构,然而该方法仍需要提前明确聚类个数和初始聚类中心,聚类结果依赖初始值的设定。文献[3]采用MCR算法(Mountain C-regression Method)[4]自动确定聚类数目和初始聚类中心。文献[5]先运行减法聚类算法,将其结果用作FCM算法的初始聚类中心,但需要预知聚类个数,得到聚类结果后采用最小二乘法直接获得结论参数,即得出初始T-S模糊模型,最后使用遗传算法整体优化T-S模糊模型的参数和结构。文献[6]提出的快速搜索密度峰聚类算法不需要预先获知聚类个数,可以快速、精确地确定聚类中心。针对差分进化算法(Differential Evolution,DE),文献[7-8]根据进化时期的不同，自适应地选择不同的变异策略,结合了两种不同进化模式中的变异操作。文献[9-10]采用的变异因子和交叉因子均为自适应因子,都提高了算法性能。

由于基本FCM算法存在依赖初始值设定、容易陷入局部最优、计算速度慢等缺点,本文将FCM算法与快速搜索密度峰聚类相结合。首先通过快速搜索密度峰聚类算法获得聚类数目,同时将其聚类结果作为FCM算法的初始聚类中心,结合最小二乘法可以快速得到初始T-S模糊模型的结论参数。最小二乘法和其他梯度法一样,有容易陷入局部最优的缺点。针对上述缺点,本文引入全局搜索能力强的差分进化算法,改进了基本差分进化算法,并整体优化模型的前后件参数,提高了T-S模糊模型的辨识精度。

1T-S模糊模型辨识

1.1概述

模糊模型主要有3种:模糊关系模型、T-S模糊模型和Mamdani模糊模型。其中T-S模糊模型拥有简单的模型结构和强大的非线性逼近能力,非常适用于建立非线性系统的近似数学模型[11],已成为研究热点。

1.2T-S模糊模型

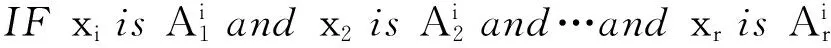
(1)

T-S模糊模型的输出为单个规则的加权平均

(2)

1.3模型辨识

1.3.1概述T-S模糊模型的辨识一般由结构辨识与参数辨识组成,结构辨识与参数辨识均包含前件部分与后件部分的辨识。模糊聚类是当前应用广泛的结构辨识方法,在合理的聚类个数与聚类中心下,模糊聚类能够实现对前件空间的最优模糊划分,并能结合各种最小二乘技术快速估计后件参数。

1.3.2结构辨识方法模糊C均值聚类(FCM)[13]算法是目前最常用的模糊聚类算法,算法结果中每一类对应模型里的一条模糊规则。给定样本集X={x1,x2,…,xr},设聚类数为c,每个样本点xj属于第i类的程度(即隶属度)表示为uij,模糊划分矩阵U=(uij)c×r,定义如下目标函数:

(3)

(1) 确定聚类数目c,初始化聚类中心V0,模糊加权指数m一般取2,给定迭代停止阈值ε,迭代计数器b=0。

(2)根据式(4)计算并更新划分矩阵

(4)

(3)

根据式(5)计算并更新聚类中心矩阵

(5)

(4)

如果‖Vb-Vb+1‖≤ε,则终止算法,获得模糊划分矩阵U和聚类中心V。否则令b=b+1,转到步骤(2)。

1.3.3参数辨识方法在前提参数已得知的条件下,本文采用最小二乘估计用于直接辨识T-S模型的结论参数[14]。由式(2),系统输出为

(6)

代入式(6),可得最小二乘形式:

Y=XP

(7)

P的最小二乘估计为

(8)

即可计算出模型的后件参数,得到初始的T-S模糊模型。

2快速搜索密度峰聚类算法

2.1概述

FCM能够快速有效地完成模糊聚类,但FCM同样存在缺点:如果无法提前明确样本集数据的聚类数目,聚类就不能进行;初始值的设定强烈影响结果,人们在不能精确设定初始聚类中心情况下通常随机设定,增加了算法陷入局部最优的可能[13]。针对上述缺点,为了防止陷入局部最优,并且提升聚类速度,本文在使用FCM之前先使用快速搜索密度峰聚类算法[7]求出聚类数目和初始聚类中心。

2.2算法简介

快速搜索密度峰聚类算法不需要人为提前明确聚类个数,只需计算各个样本点之间的距离,是一种基于其提出的距离指标和密度指标的新型聚类算法,具有速度快、精度高的特点。

对于任意数据点i,与其余数据点的欧氏距离记为dij,根据dij计算密度指标ρi和距离指标δi。密度指标定义为

(9)

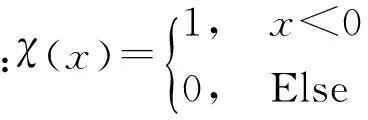
(10)

对于数据点i,其距离指标δi为全部密度比点i大的点与其距离中的最小值。如果点i的密度最大,则它的距离指标δi为全部相互距离中的最大值,即

(11)

计算出所有数据点的距离指标和密度指标后,根据两项指标作出聚类中心抉择图,可利用图像找出聚类中心和所有类簇。如图1、图2所示。

图1　数据点分布图

对图1中28个数据点根据式(10)和式(11)计算出每个点的密度指标和距离指标,可得到横轴为密度、纵轴为距离的聚类中心抉择图。聚类中心附近的数据点密度ρi会较大,但仍然低于各自属于的聚类中心或者其他更靠近聚类中心的点,因此,它们的距离δi值普遍很小;对于聚类中心来说,密度ρi值都较大,密度指标比它们大的点只可能为其他聚类中心,因此,它们的距离δi值都较大;对于异常点,如数据点26、27、28,这些点周围几乎没有其他数据点,并且远离其他类簇,因此,它们具有非常小的密度指标和较大的距离指标。经过上述分析,可以很清楚地在聚类中心抉择图中找出聚类中心,如图2中,可判断聚类数目为2,聚类中心为数据点1和10。

图2　聚类中心抉择图

3改进的差分进化算法

3.1概述

由于模糊C均值聚类算法比较依赖初始值设定,在迭代过程中容易陷入局部极小点;最小二乘法属于梯度法,同样容易陷入局部极小点。差分进化算法(DE)[15]是一种随机的并行全局搜索算法,拥有简单易用、鲁棒性高和全局搜索能力强等特点,可以用来克服上述缺陷。使用最小二乘法辨识得到初始T-S模糊模型,用改进的差分进化算法调整模型参数,得到更加精确的模糊模型。

3.2算法流程

改进的DE算法流程如下:

(1)编码和种群初始化。G=0,1,2,…,Gm表示进化代数,第G代种群中的第i个个体Xi,G表示为

(12)

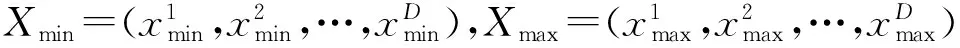
优化T-S模糊模型时,应该一并优化隶属度函数和模糊规则,这样不仅调整了模型结构,也优化了模型参数。文献[5]使用遗传算法对模糊模型的参数和结构进行整体优化,染色体编码的参数为隶属度函数的中心v和方差σ以及结论参数p,每条染色体包含(3n+1)c个实数,这里n是输入变量的维数,c是数据集聚类个数。采用此种编码,本文改进DE算法中D=(3n+1)c,[Xmin,Xmax]以FCM和最小二乘法获得的初始参数为中心产生。当G=0时,初始种群中的第i个个体Xi,0为(v11,…,vcn,σ11,…,σcn,p11,…,pcn),其余的NP-1个个体均按此种格式编码,在[Xmin,Xmax]内随机均匀产生,从而形成初始种群。

(2)变异操作。差分进化算法的进化模式[16]有多种,标准DE的进化模式是其中的DE/rand/1/bin,变异策略如式(13)。

(13)

对种群中每个个体Xi,G,随机产生3个相互不同的整数r1,r2,r3∈{1,2,…,NP},且要求r1,r2,r3,i这 4个数相互不同。 另一种常用的进化模式为DE/best/1/bin,

(14)

这里Xbest,G代表目前种群里的最优个体。若Vi,G不在[Xmin,Xmax]范围中,则令Vi,G=Xmin+rand(0,1)·(Xmax-Xmin),其中rand[0,1]是[0,1]区间中均匀分布的随机数。

这两种进化模式,前者善于维持种群多样性,然而收敛速度比较慢；而后者则是收敛速度比较快,但容易陷入局部极小点。为了充分发挥DE/rand/1/bin的全局搜索能力和DE/best/1/bin快速收敛的能力,克服这两种进化模式的缺点,文献[7]将这两种进化模式的变异操作方式结合使用,自适应地选择变异策略,具体如下:

(15)

(16)

经过测试比较,本文使用新的非线性阈值如下：

(17)

其中[φmin,φmax]=[0.1,1]。在算法初期,φ值较小,DE/rand/1/bin被使用的概率较大,随着进化代数的增加,将更多地使用DE/best/1/bin,这样算法在全局搜索和收敛速度之间进行了平衡。

式(13)、式(15)中的F为变异尺度因子,在标准DE中是一个常量。当F较大时,算法容易逃出局部极小点,但是收敛的速度会变慢,反之,算法虽然收敛速度变快,却容易陷入局部极小点。采取自适应机制对F进行赋值,文献[9]采用式(18)线性递增调整变异因子。

(18)

基于上述线性变化策略,本文使用新的非线性变化策略如下：

(19)

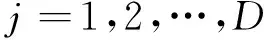
(20)

其中：randj是位于[0,1]间的均匀分布的随机数,randnj是属于{1,2,…,D}内随机生成的维数索引号；CR为交叉概率因子,在标准DE中是处于[0,1]间的一个常量。当CR较大时,算法容易发生早熟收敛现象,反之,算法稳定,成功率高,种群多样性能够得到很好的保持,但收敛速度慢。采取自适应机制对CR进行赋值,文献[10]采用式(21)线性递减调整交叉因子。

(21)

同样改用非线性变化策略

(22)

F随着迭代次数的增加,由大变小,而CR则由小变大,在算法开始的时候充分保证种群的多样性和算法的全局寻优能力,在算法的后期适当减少种群的多样性,促进算法尽快收敛。

(4)选择操作。选择操作遵循“贪婪选择”策略,候选个体Ui,G与目标个体Xi,G进行竞争。

(23)

式中：f是适应度函数,对于Ui,G和Xi,G,取适应度函数值更佳者作为第G+1代个体,取代原来的第G代个体,并使迭代计数器G增加1。式(23)适合最小化问题的处理。

(5)终止条件。假如种群Xi,G符合终止条件或者到达最大迭代次数Gm,则获得最优解;否则转至步骤(2),直至满足条件为止。

3.3建模过程归纳

本文建模及优化算法流程如图3所示。

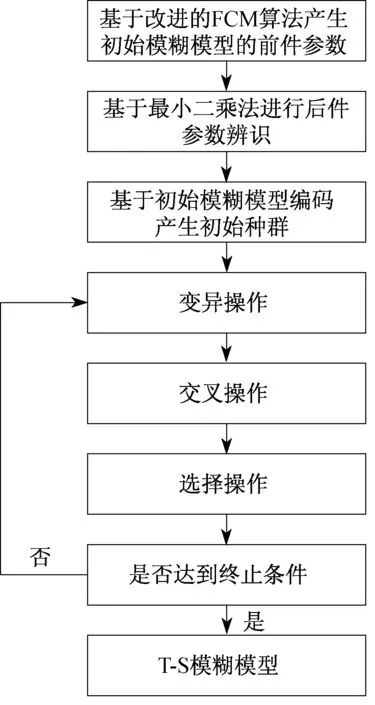
图3　T-S模糊模型建模过程流程图

4仿真实验和结果分析

著名的Box和Jenkins煤气炉数据经常被研究者选取为检验辨识方法是否合理的标准实验数据。该系统为SISO动态系统,包含296组输入输出数据,其中输入变量x(k)为煤气流量,输出变量y(k)为CO2浓度,k表示采样间隔,且k=9 s。本文选择煤气流量x(k-1)及CO2浓度y(k-1),y(k-2)作为模糊模型的输入,输出是k时刻的CO2浓度y(k),选择前148组数据作为训练集用来辨识模型,余下的148组数据作为测试集。

对训练集输入数据由快速搜索密度峰聚类算法得到图4所示的聚类中心抉择图。

经判断,将图4中被圈出的点作为FCM的初始聚类中心,同时得到聚类个数c为3,通过FCM和最小二乘法(LS)得到初始T-S模糊模型;分别使用本文的改进DE算法和两种基本DE算法(分别采用DE/rand/1/bin和DE/best/1/bin变异模式,记为DE1和DE2)对模型参数进行优化。DE算法中种群个体维数D为30,种群规模NP为10D,进化代数Gm为300,适应度函数f取模型的均方误差MSE。

在DE1和DE2中,F=0.5,CR=0.9；本文改进DE算法中,F∈[0.2,0.5],CR∈[0.6,0.9]。

图4　聚类中心抉择图

为了评价模型效果,使用如下几项评价标准,包括均方误差(MSE)、平均绝对百分误差(MAPE)以及平均绝对误差(MAD)。

分别利用训练集实际输出和测试集实际输出与模型输出作比较,得到模型误差如表1和表2所示。

表1　训练集模型误差比较

采用训练集时,3种DE算法迭代收敛曲线如图5所示。

表2　测试集模型误差比较

图5　收敛曲线

由表1和表2可知,本文提出的改进DE算法的各项评价指标均最小,故对模型参数的优化效果最佳。由图5可知,DE2的收敛速度最快,其次是改进DE,DE1的收敛速度最慢;DE2在100代左右收敛,改进DE在160代左右收敛,而DE1在300代内都还未收敛。本文提出的改进DE收敛速度比DE2略低,但收敛精度较高,在全局搜索和收敛速度之间进行了平衡,有效提高了收敛精度和模型辨识精度。

本文方法得出的T-S模糊模型,其训练集模型输出和测试集模型输出与实际输出的比较如图6和图7所示。可见,模型输出曲线与实际输出曲线拟合良好,表明此模型拥有优良的拟合精度和泛化能力。

图6　训练集模型输出与实际值比较

图7　测试集模型输出与实际值比较

将296组数据全部作为训练集进行辨识,表3列出了其他模糊模型辨识方法在相同性能指标MSE下的结果。从表中可以看出,与其他方法相比,本文方法拥有更高的辨识精度。

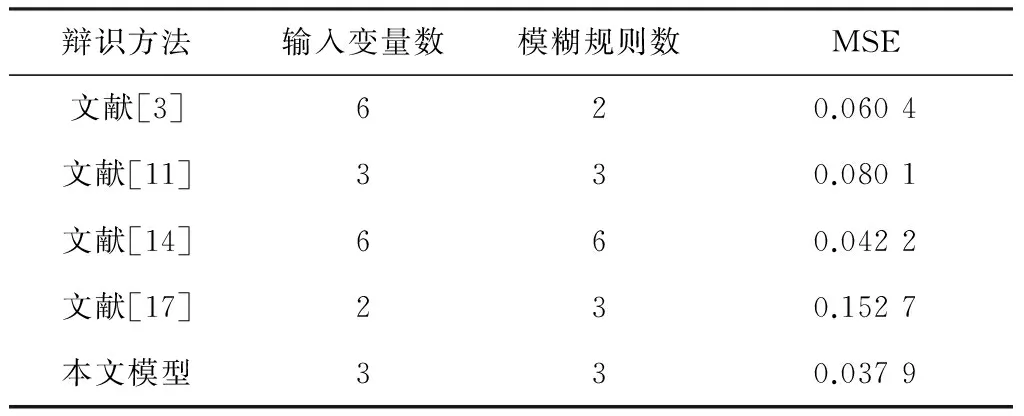
表3　不同辨识方法结果比较

5结束语

针对复杂非线性系统的建模问题,本文提出了一种改进的T-S模糊模型建模及优化方法。快速搜索密度峰聚类算法可以快速得到聚类数目和聚类中心,与FCM相结合,弥补了FCM需要提前明确聚类数目和依赖初始值设定的缺点。对基本DE算法的编码初始化、交叉和变异因子以及进化模式进行了改进,在全局搜索和收敛速度之间进行了平衡,提高了收敛精度。使用改进的DE算法整体优化模型的结构和参数,得到最终的T-S模糊模型。选取Box和Jenkins煤气炉数据,在MATLAB中对其系统进行了仿真,并与其他建模方法进行了比较,验证了本文方法可以快速、有效地提高非线性系统的模型辨识精度。

参考文献：

[1]马俊峰,张庆灵.T-S模糊广义系统的逼近性[J].控制理论与应用,2008,25(5):837-844.

[2]CHENG Weiyuan,JUANG Chia-Feng.An incremental support vector machine-trained TS-type fuzzy system for online classification problems[J].Fuzzy Sets and Systems,2011,163(1):24-44.

[3]林妹娇,陈水利.一种新的TS模型辨识算法[J].集美大学学报(自然科学版),2013,18(3):219-224.

[4]WU Kulung,YANG Minshen,HAIEH Junenan.Mountain c-regression method[J].Pattern Recognition,2010,43:86-98.

[5]李盼盼.基于T-S模型的非线性系统模糊辨识方法研究[D].江苏镇江:江苏大学,2008:1-5.

[6]ALEX R,ALESSANDRO L.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[7]呼忠权.差分进化算法的优化及其应用研究[D].河北秦皇岛:燕山大学,2013.

[8]陈亮.改进自适应差分进化算法及其应用研究[D].上海:东华大学,2012.

[9]DAS S,KONAR A,CHAKRABORTY U K.Two improved differential evolution schemes for faster global search[C]//Genetic and Evolutionary Computation Conference,GECCO 2005.Washington DC,USA:ACM,2005:991- 998.

[10]谢晓锋,张文俊,张国瑞,等.差异演化的实验研究[J].控制与决策,2004,19(1):49-52,56.

[11]钱富才,伍光宇.一种T-S模型的在线辨识算法[J].控制与决策,2015,30(2):343-347.

[12]刘福才,窦金梅,王树思.基于智能优化算法的T-S模糊模型辨识[J].系统工程与电子技术,2013,35(12):2643-2650.

[13]温重伟,李荣钧.改进的粒子群优化模糊C均值聚类算法[J].计算机应用研究,2010,27(7):2520-2522.

[14]王洪斌,刘少岗,李瑶瑶,等.基于自适应模糊聚类的T-S模糊辨识方法[J].模糊系统与数学,2014,28(5):137-142.

[15]GUO Haixiang,LI Yanan,LI Jinling,etal.Differential evolution improved with self-adaptive control parameters based on simulated annealing[J].Swarm and Evolutionary Computation,2014,19:52-67.

[16]EPITROPAKIS M,TASOULIS D,PAVLIDIS N.Enhancing differential evolution utilizing proximity-based mutation operators[J].IEEE Transactions on Evolutionary Computation,2011,15(1):99-119.

[17]张椿玲,黄景廉,曾贤强.一种基于模糊聚类的模糊辨识方法[J].计算机应用与软件,2012,29(2):216-217.

Improved Modeling and Optimization of T-S Fuzzy Models

LIU Jun,YIN Xiao-ming,GU Xing-sheng

(Key Laboratory of Advanced Control and Optimization for Chemical Processes,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China)

Abstract:Fuzzy modeling is an effective method for nonlinear systems,but there exist many unsolved issues due to the complexity of nonlinear system.This paper proposes an improved modeling and optimizing method for T-S fuzzy models.Firstly,we combine the fast search method of density peaks with the fuzzy cluster method (FCM),in which the former is utilized to find the initial clustering center and then the latter achieves the cluster.Secondly,the initial T-S fuzzy model is obtained by using the least square method to identify these parameters.And then,an improved differential evolution algorithm is utilized to optimize the above structure and parameters.Finally,the experimental results over a representative example show that the proposed method can improve the identification precision and convergence speed for T-S fuzzy model.

Key words:fuzzy modeling; T-S model; FCM; clustering by fast search of density peaks; DE

收稿日期：2015-07-31

基金项目：国家自然科学基金(61573144)

作者简介：刘骏(1990-),男,安徽人,硕士生,主要研究方向为复杂工业过程建模、控制与优化。E-mail:1017584186@qq.com 通信联系人：顾幸生,E-mail:xsgu@ecust.edu.cn

文章编号：1006-3080(2016)02-0233-07

DOI:10.14135/j.cnki.1006-3080.2016.02.013

中图分类号：TP273+.4

文献标志码：A