一种改进的细菌觅食优化算法
2016-06-22孙京诰
刘 珍, 孙京诰
(华东理工大学信息科学与工程学院,上海 200237)
一种改进的细菌觅食优化算法
刘珍,孙京诰
(华东理工大学信息科学与工程学院,上海 200237)
摘要:针对细菌觅食优化算法存在收敛速度慢、寻优精度低、易陷入局部最优等缺点,提出了一种改进的细菌觅食优化算法。改进原有固定步长的游动方式,引入自适应步长调整策略,提出了基于非线性递减的余弦自适应步长;改进细菌位置的更新方式,借鉴人工蜂群的方法,采用混合的更新方式;改进优胜劣汰的选择标准,保留最优个体,对复制后的父代个体引入杂交算子;改进迁徙方式,提出种群进化因子,防止进化停滞不前。将本文算法用于经典函数以及PID参数整定测试,仿真实验结果验证了该算法的有效性。
关键词:细菌觅食优化算法; 自适应步长; 位置更新方式; 杂交算子; 种群进化因子
20世纪40年代以来,实际工程问题呈现出越来越多的复杂性,包括多极值、强非线性、多约束性和高维度等。传统的优化方法已经不能解决诸多实际生产、生活中所面临的复杂问题,智能优化算法应运而生。细菌觅食优化算法[1]作为一种新型的智能优化算法具有良好的全局优化能力、鲁棒性强以及算法简单等优点,受到了不同领域的关注[2-4]。
针对步长固定的问题,Chen等[5]提出了自适应搜索的细菌觅食优化算法;刘小龙等[6]提出了灵敏度的概念,对细菌的游动步长加以调节;Niu等[7-8]在验证了步长大小的选取对全局收敛的快速性和全局最优解的获得具有重要影响的基础上,提出了线性递减与指数非线性递减的自适应步长;Mishra[9]提出了基于TS模糊机制来选取最优步长。算法融合方面,Biswas等[10]提出了一种基于差分算法和BFO(Bacterial Foraging Optimization)算法的混合全局优化算法,除此之外,与BFO算法相结合的算法还有粒子群算法[11]、遗传算法[12]等。细菌觅食算法已经在电气控制、模式识别、生产调度等方面得到广泛应用。
本文针对细菌觅食优化算法存在收敛速度慢、寻优精度低、易陷入局部最优等缺点,改进了原有固定步长的前进方式,引入了自适应步长调整策略;位置更新方面,借鉴蜂群的方法,采用了混合的更新方式;改进了复制操作中优胜劣汰的选择机制,并对复制后除当前最优父代外的其他父代细菌除引入了交叉算子;在迁徙操作中引入了种群进化因子,提出了一种改进的细菌觅食优化算法用于经典函数以及PID参数整定测试,仿真实验结果验证了该算法的有效性。
1细菌觅食优化算法
1.1概述
细菌觅食优化算法是根据大肠杆菌的觅食行为提出的。大肠杆菌根据所处的环境来改变身体表面鞭毛的旋转方向,使其进行翻转与游动,以期寻找到丰富的食物源,避开有毒区域。
同其他细菌一样,经过一段时间后,根据优胜劣汰的自然选择机制,部分大肠杆菌会淘汰、消亡,而存留下来的大肠杆菌会进行自我繁殖。此外,所处环境的变化,也会导致该区域细菌的消亡或增生。细菌游动和翻转如图1所示。

图1 细菌游动和翻转示意图
通过模拟大肠杆菌的觅食行为,细菌觅食优化算法主要由趋向性操作、复制操作和迁徙操作组成。
1.2趋向性操作
趋向性操作是算法的核心操作,模拟的是大肠杆菌游动和翻转的觅食行为。在环境较差的区域,细菌会翻转得比较频繁,而在环境较好的区域,细菌则会较多地游动。设细菌的种群规模为S,维度为n,则细菌i的位置用维度为n的向量表示。细菌觅食优化算法采用随机初始化的方式初始化细菌的位置,初始化公式如下:
(1)
细菌i的趋向性操作可用式(2)、式(3)表示:
θ(i,j+1,k,l)=θ(i,j,k,l)+C(i)×φ(i,j)
(2)
(3)
其中:θ(i,j,k,l)表示细菌i在第j次趋向性操作、第k次复制操作和第l次迁徙操作时的位置,代表着所在优化区间内的一个可行解;C(i)为细菌i的趋向性步长;φ(i)为细菌i翻转时在随机方向上的一个随机单位方向向量;Δ(i)为一个随机向量。
1.3复制操作
根据优胜劣汰的自然机理,经过一段时间后,觅食能力弱的细菌最终会被淘汰,而觅食能力强的细菌则会繁衍后代,维持种群的规模。通过模拟此现象,提出了复制操作。
根据细菌觅食能力的强弱,选择适当的评价指标函数,即适应度函数。通过对细菌i在趋向性操作中经历的所有位置的适应度总和进行优劣排序,淘汰排在后面的占50%种群数的细菌。对于保留下来的细菌进行复制操作,各自生成的新个体与自身完全相同,具有相同的觅食能力、相同的位置。复制操作维持了种群规模的不变性。
1.4迁徙操作
当细菌所处周围环境由于各种原因而突然发生变化或者逐渐改变时,可能会使此局部区域的细菌群集体死亡或集体迁移。通过模拟此现象,提出了迁徙操作。
迁徙操作以一定的概率发生,当细菌个体满足迁徙发生的概率时,则这个细菌个体死亡,并在解空间的任意位置上随机产生一个新的个体,这个细菌个体可能会拥有与原细菌不同的细菌觅食能力,有利于跳出局部最优解,促进全局最优解的寻找。设迁徙概率为Ped,种群规模为S,则细菌迁徙操作的流程如图2所示。
设细菌执行趋向性操作、复制操作和迁徙操作的次数分别为Nc、Nre、Ned,用参数j、k、l分别对其计数,计数参数初始时设置为0,细菌觅食优化算法的流程图如图3所示。
2改进的细菌觅食算法
2.1概述
针对BFO算法收敛速度慢、易陷入局部最优的缺点,本文提出ABFO(Adaptive Bacterial Foraging Optimization)算法,从以下几个方面改进BFO算法:
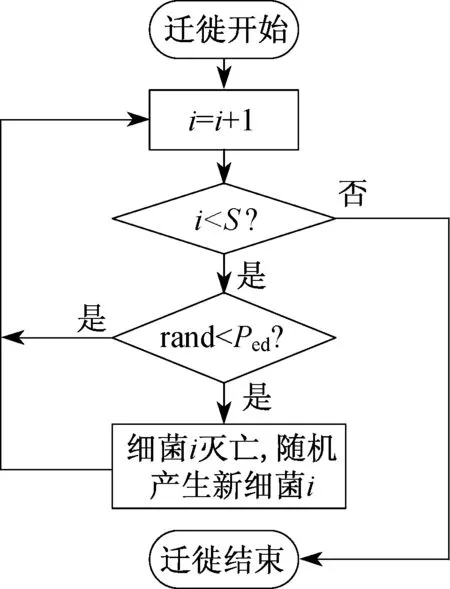
图2 迁徙操作流程图

图3 细菌觅食优化算法流程图
(1)改进趋向性操作。引入自适应策略,将固定步长改为自适应步长,随着迭代次数的增加而减少,同时借鉴蜂群的方法,采用混合的位置更新方式对细菌进行趋化操作。
(2)改进复制操作。改进优胜劣汰的选择机制,根据细菌当前适应度值的优劣进行排序,同时对于复制后的半数细菌,保留其中的精英个体,并对此半数细菌剩下的细菌引进交叉算子。
(3)改进迁徙操作。引入种群进化因子,防止种群进化不前,陷入局部最优。
2.2趋向性操作的改进
2.2.1趋向性步长的改进步长的选择对于细菌觅食优化算法的性能有直接的影响,较大的步长易于全局搜索、寻找最优解,但精度不够,可能会由于步长过大而错失全局最优解;较小的步长可以提高精度,但全局收敛速度慢,同时也可能会陷入局部最优;固定的步长难以平衡全局搜索与局部搜索的要求。因此,为了配合BFO算法初期的全局搜索以及后期的局部搜索对步长的要求,本文提出了一种基于余弦的自适应步长,改进原有的固定步长。由于余弦函数在区间(0,π)的函数值是递减的,步长C随着迭代次数的增加而非线性递减,使得算法在初期以较大的步长进行全局搜索,缩小最优解可能所在的区域,在算法后期则用较小的步长对缩小的区域范围进行局域搜索,这一规律与觅食行为相符合。基于余弦的自适应步长C的计算公式如下:
(4)
其中:Cmin≤C≤Cmax;gen为当前迭代次数;genm为最大迭代次数。
2.2.2位置更新方式的改进算法的融合是算法改进的重要方向,细菌觅食算法和人工蜂群算法具有不同的产生新个体的方式,拥有不同的寻优效果,本文借鉴蜂群算法,采用混合的位置更新方式来更新细菌的位置。假设种群规模为S,其中的半数细菌s1按照原BFO算法中的方式更新位置,剩下的半数细菌s2则按照人工蜂群的更新方式更新位置。因此,菌群s1、s2的位置更新方式分别为式(5)、式(6)。θ(i,j+1,k,l)=θ(i,j,k,l)+C×φ(i,j)
(5)
θ(i,j+1,k,l)=
θ(i,j,k,l)+rand×(θ(i,j,k,l)-θ(r,j,k,l))
(6)
其中:r为在当前种群S中随机选择的一个不等于i的细菌,即r≠i,且r∈{1,2,…,S}。式(6)中θ(i,j,k,l)-θ(r,j,k,l)在本质上相当于步长向量,随着迭代次数的增加,搜索空间缩小,θ(i,j,k,l)与θ(r,j,k,l)之间的距离减小,即步长向量长度减小,步长的动态调整有利于算法精度的提高。采用不同的更新方式,使得细菌位置更新得多样化,又不失去算法分析的合理性。混合的更新方式有利于种群多样化的保持以及最优解的获得。
此外,为了防止进化停滞,加强细菌趋向性的有效性,引入相应的计数参数trail,用于记录个体位置连续未得到改善的次数,当细菌对应的trail达到一定的数值时,根据迭代次数,对该细菌的位置进行重新初始化或扰动。
2.3复制操作的改进
原有的BFO算法是对细菌趋向性操作经过的所有位置的适应度值的和进行优劣排序,由于细菌位置是在趋向性操作下逐步加强改善的,是细菌所经历的历史最优值,细菌的当前位置更能反映细菌的觅食能力,而且采用细菌的当前位置能够降低算法的复杂度,因此,本文采用当前细菌位置的适应度值进行优劣排序,对优秀的半数细菌S/2进行复制,复制后的子代替换原细菌种群中较差的S/2细菌。
由于复制后的新种群规模为S的细菌群中,每个父代都有一个与其相同的子代,降低了种群的多样性。因此,为了增加种群的多样性以及防止最优个体的丢失,本文对父代个体(除了最优父代外)引入了杂交算子,与最优个体进行杂交,杂交公式如下:
(7)
2.4迁徙操作的改进
迁徙操作的存在有利于跳出局部最优解,寻找全局最优解。BFO算法按照给定的固定概率进行迁徙,没有考虑种群的进化情况。根据种群的进化情况进行迁徙,有利于算法寻优的有效性。当种群进化程度较快时,种群群体处在快而有效的寻优状态,以较低的迁徙概率进行迁徙,可以保留当前有利的位置信息;当种群进化程度较慢时,种群群体很大程度上陷入了局部最优,需要以较高的迁徙概率进行迁徙,跳出局部最优解,防止种群进化不前。本文改进了原有BFO算法中的迁徙操作,引入了种群进化因子f。
(8)
其中:fgen代表第gen代的最优适应度值;rand作用是防止分母为0。当f=0时,进化停滞;当0
2.5ABFO算法流程
(1) 初始化参数,生成初始种群
(2) Forl=ltoNedDo
(3)Fork=ktoNreDo
(4) Forj=jtoNcDo
(5)Fori=itos1Do
(6) 自适应步长,细菌位置原更新方式
(7)End For
(8)Fori=s1+1 toSDo
(9) 自适应步长,细菌位置新更新方式
(10)End For
(11) End For
(12) 改进的复制操作
(13) End For
(14) 基于种群进化因子的迁徙操作
(15)End For
3仿真实验与分析
3.1函数测试
本文采用表1所示的8个标准测试函数对BFO、DBFO[13]以及ABFO的性能分别进行测试对比。这些函数的全局最优解采用常规的方法通常较难获得,而且随着函数维数的升高,优化难度会急剧增加。

表1 标准测试函数
本文算法的参数选取参考文献[13],将测试函数的维度设为30,细菌种群规模为40,固定步长为0.01×区间长度,趋化次数Nc=40,游动次数Ns=5,复制次数Nre=5,迁徙次数Ned=5,迁徙概率Ped=0.25。BFO、DBFO和ABFO 3种算法在每个测试函数上的运行次数均为20次。测试结果的精度达到10-15等级时,以0代替,测试结果见表2。BFO、DBFO以及ABFO 3种算法的运行时间经四舍五入保留一位小数点后的数据如表3所示。其中,DBFO算法在表中的实验结果均参照文献[13],由于原文献并未给出标准差,因此,本文在此项中用*号表示。

表2 函数测试运行结果
由表2可以看出,在8个标准测试函数中,除了ABFO与DBFO算法对于测试函数f2所求得的最优解持平之外,ABFO算法所求得的最优解均优于DBFO算法和BFO 算法,并且在易陷入早熟收敛的Rosenbrock函数f5、较难获得全局最优解的Rastrigrin函数f6和Acklley函数f7中,ABFO算法的最优解精度达到了0,提高了寻优精度和寻找全局最优解的能力,突破了BFO算法易陷入局部最优解的缺点。但是由最差解和平均解可知,ABFO算法寻优的整体水平还有待提高。
由表3可知,ABFO算法的时间复杂度最低、收敛速度最快。在DBFO算法中,由于双种群的存在,其种群规模为80,若将其时间折半,考虑到趋向性操作中最大游动步数的存在,可以认为DBFO算法运行所需要的时间与BFO算法运行所需要的时间相差无几,具有相同的时间复杂度。
算法的收敛性是检测算法性能的重要指标,选取测试函数f7、f8加以测试。算法收敛性能曲线如图4所示。测试结果表明,本文的改进算法针对测试函数f7、f8最优解的寻优均能较快收敛,验证了算法的收敛性能。
由表2、表3可知,本文改进的ABFO算法无论在寻优精度、运行速度,还是全局优化能力方面,均优于BFO算法和DBFO算法。图4所示的收敛性能测试曲线也表明了该算法良好的收敛性能。函数测试的仿真实验结果表明ABFO算法的有效性。
3.2应用实例
PID控制器是目前应用最为广泛的控制器,PID控制器的参数整定是控制系统设计的核心内容。PID控制系统框图如图5所示。

表3 函数测试运行时间
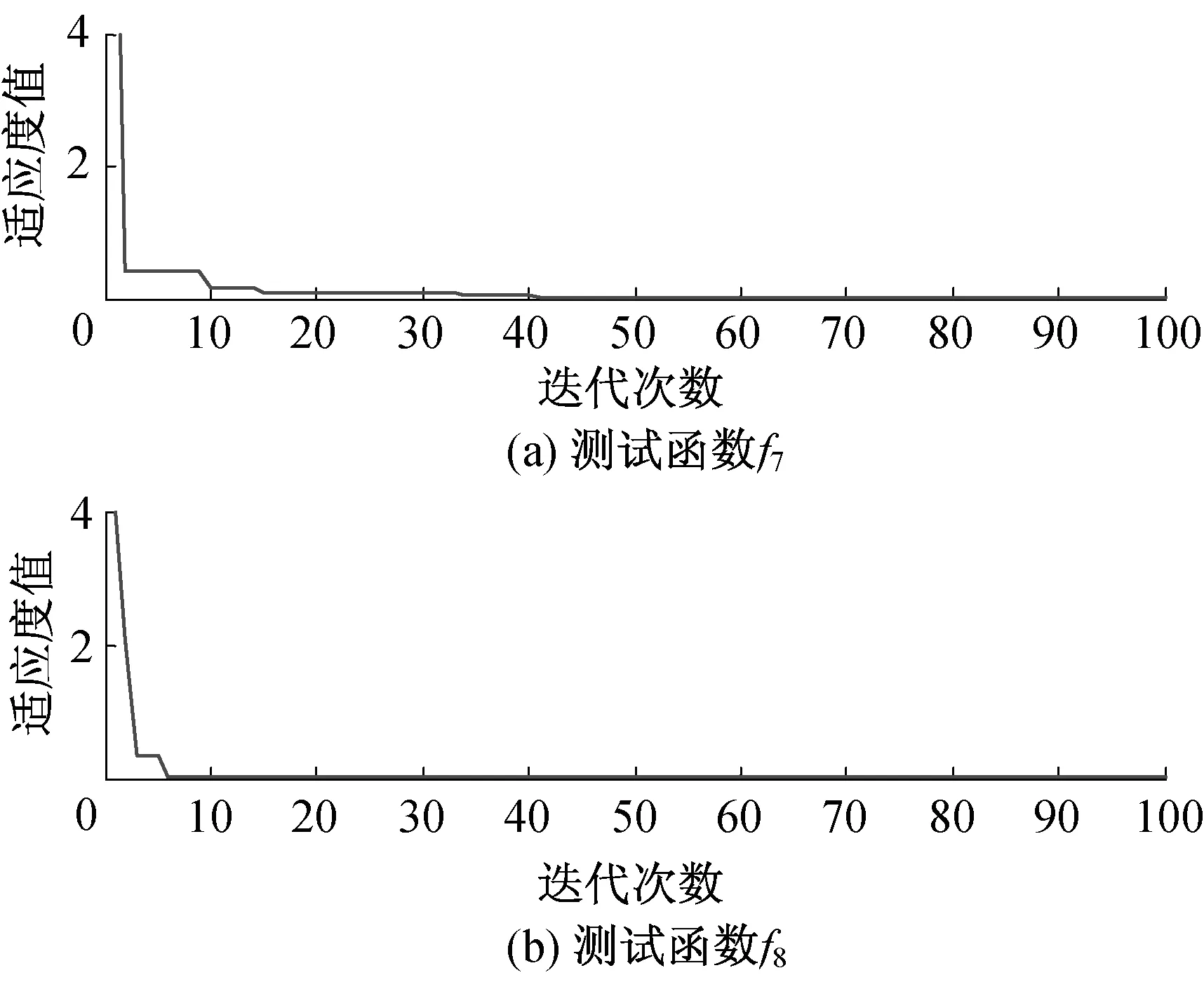
图4 算法收敛性能测试曲线

图5 PID控制系统框图
图中,r(t)为系统输入;e(t)为系统偏差,也为控制器输入;u(t)为控制器输出;y(t)为系统输出。设PID控制的传递函数C(s)的表示形式为
(9)
其中,Kp、Ti、Td分别表示比例系数、积分时间常数和微分时间常数,三者都是可调的参数。PID控制器的输出信号u(t)为
(10)
参照文献[2],选取被控对象的传递函数G(s)为
(11)
本文将BFO算法、DBFO算法、ABFO算法分别用于PID参数整定。PID参数的优化整定就是在Kp、Ti、Td的可行域内寻找到一组控制参数,在满足系统稳定的前提下,使选取的性能指标最优[14],使系统拥有较优的控制品质[15]。针对BFO算法、DBFO算法以及ABFO算法,本文选取常用的性能指标ITAE作为优化算法的适应度评价函数J,如式(12)所示。
(12)
BFO算法、DBFO算法、ABFO算法整定PID控制器的框图如图6所示。

图6 BFO、DBFO、ABFO优化PID系统框图
本文采用MATLAB软件进行仿真。在simulink仿真实验中,采用单位阶跃函数作为系统输入,设置simulink系统模块仿真时间为10 s。优化算法通过调用simulink系统模块,将寻优参数赋值给系统模块,经过系统每次仿真得出结果,计算系统性能评价函数,根据得出的性能评价函数来指导算法的寻优,如此循环往复,直到达到算法的最大迭代次数,算法寻优结束,从而得出一组最优的PID参数。
在PID参数整定优化中,BFO算法、DBFO算法以及ABFO算法的基本参数设置为:种群规模S=20,维度n=3,Ns=5,Ped=0.25。根据算法参数对算法性能的影响,选取Nc、Nre、Ned3个参数为三因素,选用正交表L9(34)安排试验。通过正交试验,得出三参数在BFO、DBFO、ABFO中取值的优化方案分别为(15,4,4)、(15,2,6)、(15,4,6)。PID参数整定方法有很多,为了更好地测试ABFO算法的PID参数整定效果,本文还加入了工程整定方法中的衰减曲线法进行PID参数整定。
BFO、DBFO、ABFO算法分别运行10次所得的PID控制系统参数,以及衰减曲线法所得到的控制系统参数如表4所示,相应的单位阶跃响应曲线如图7所示。其中,J、Jm、Jw分别表示算法在运行的10次中所求得的适应度值的最优值、平均值和最差值;算法BFO、DBFO、ABFO中的Kp、Ti、Td为最优适应度J时相应的值,σ、tr、ts分别表示相应的超调量、上升时间、稳定时间。

表4 控制系统参数
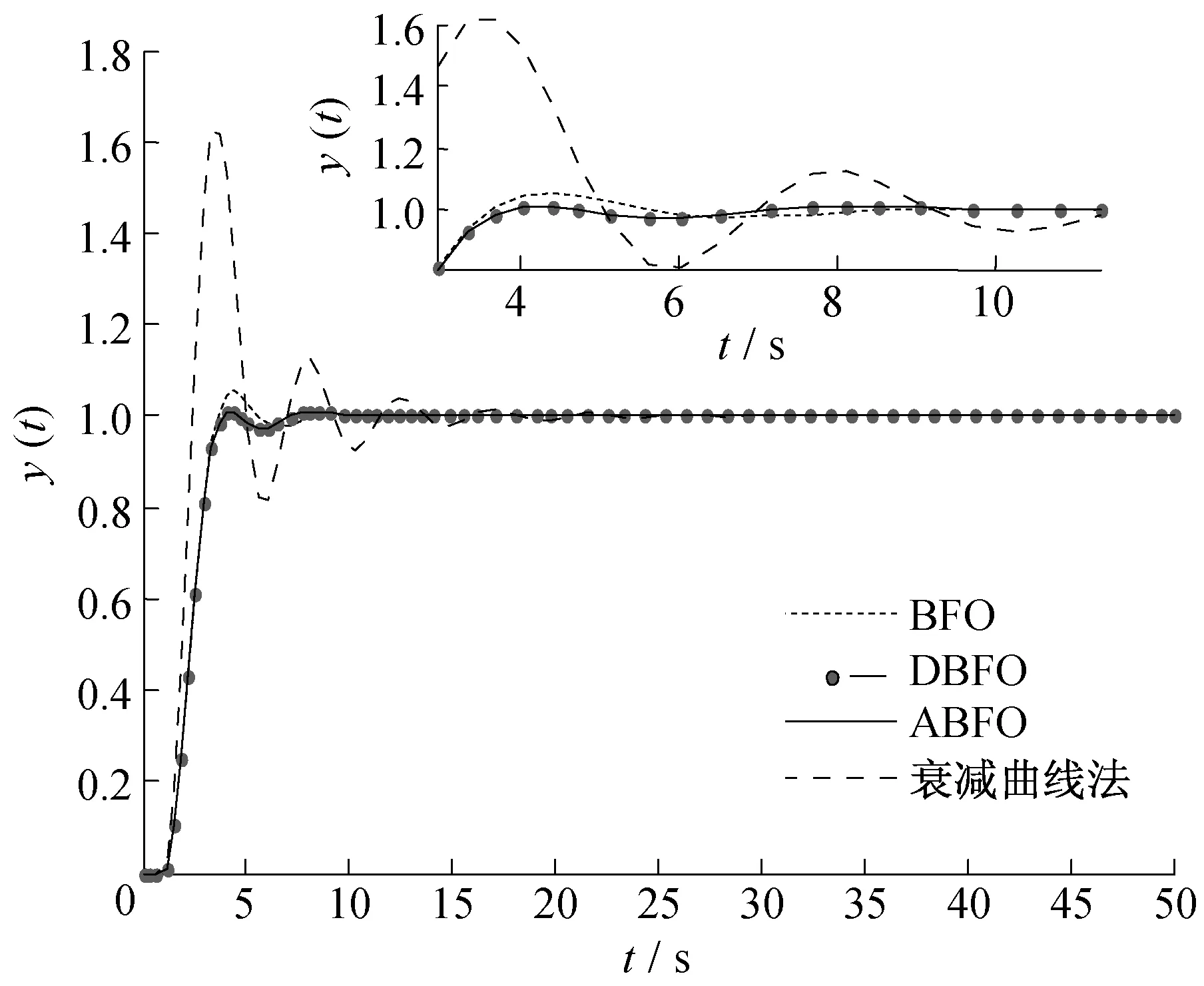
图7 阶跃响应曲线
由表4及图7可知,ABFO算法寻优所得的评价函数的适应度值最好,DBFO算法次之;衰减曲线法整定PID参数时,所得系统阶跃响应的超调量最大,稳定时间最长,而ABFO算法的稳定时间最短,与DBFO算法相当;ABFO算法所得系统的阶跃响应速度与DBFO、BFO算法相当,仅次于衰减曲线法的响应速度。因此,在PID整定方面,相比于BFO算法、DBFO算法以及衰减曲线法,ABFO算法对控制器参数整定的综合控制效果最好,具有更好的控制品质。
为了进一步验证ABFO算法的性能,本文在PID参数整定过程中加入了一个干扰,采用幅值为0.2的阶跃信号作为扰动信号,并在20 s时开始对系统进行干扰。将BFO算法、DBFO算法、ABFO算法以及衰减曲线法用于具有扰动系统的PID参数整定,算法寻优所得的最优解及相应的性能指标如表5所示,其相应的系统阶跃响应曲线如图8所示。

表5 基于扰动的控制系统参数
由表5及图8可知,ABFO算法求得的适应度值性能指标的最优值和平均值均最小,DBFO算法次之,BFO算法最差;当系统具有扰动时,用衰减曲线法求解的PID参数整定效果依然最差;ABFO算法、DBFO算法、BFO算法相对应系统的阶跃响应曲线相差无几。因此,对具有输出扰动的系统进行PID参数整定时,ABFO算法依然具有最好的综合控制性能。
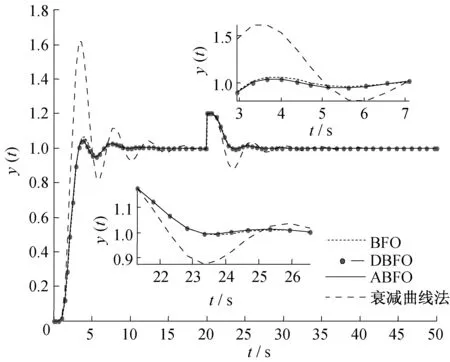
图8 基于扰动的阶跃响应曲线
4结论
本文通过对BFO算法的介绍与分析,针对其收敛速度慢、寻优精度低以及易陷入局部最优解的特点,改进了BFO算法。在趋向性操作中,将固定步长改为随迭代次数增加而逐渐减少的自适应步长,提高了算法的局部搜索能力,同时改进了细菌位置的更新方式,采用了混合的位置更新方式,有利于种群的多样性的保持;在复制操作中,按照细菌当前位置的适应度值排序,替代原BFO算法趋向性操作中所有的适应度和排序,减少了算法的复杂度,并更加准确地反映了细菌觅食的能力,同时在保留最优个体的情况下,对复制后的父代引入杂交算子,提高了种群的多样性;在迁徙操作中,引入种群进化因子,替代固定的迁徙概率,有利于细菌寻优的有效性,防止种群进化停滞不前。函数仿真测试以及PID参数整定的仿真实验结果表明,本文提出的改进的细菌觅食优化算法(ABFO算法),提高了寻优精度、收敛速度以及全局寻优的能力。
参考文献:
[1]PASSINO K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control System Magazine,2002,22(3):52-67.
[2]吕振,沈建国.改进的细菌觅食优化算法[J].计算机系统应用,2014,23(5):182-187.
[3]周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21.
[4]李娜,雷秀娟.细菌觅食优化算法的研究进展[J].计算机技术与发展,2014,24(8):39-44.
[5]CHEN Hanning,ZHU Yunlong,HU Kunyuan.Self-adaptation in bacterial foraging optimization algorithm[C]//2008 3th International Conference on Intelligent System and Knowledge Engineering(ISKE 2008).Xiamen:IEEE,2008:1026-1031.
[6]刘小龙,赵奎领.基于免疫算法的细菌觅食优化算法[J].计算机应用,2012,32(3):634-637.
[7]NIU Ben,FAN Yan,ZHAO Pei.A novel bacterial foraging optimizer with linear decreasing Chemotaxis step[C]//2nd International Workshop on Intelligent Systems and Applications (ISA).Wuhan:IEEE,2010:1-4.
[8]NIU Ben,WANG Jingwen,WANG Hong.Bacterial-inspired algorithms for solving constrained optimization problems[J].Neurocomputing,2015,148(9):54-62.
[9]MISHRA S.A hybrid least square-fuzzy bacterial foraging strategy for harmonic estimation[J].IEEE Transaction on Evolutionary Computation,2005,9(1):6l-73.
[10]BISWAS A,DASGUPTA S,DAS S,etal.A synergy of differential evolution and bacterial foraging algorithm for global optimization[J].Neural Network World,2007,17(6):607-626.
[11]田亚菲,张范勇,阎石.基于粒子群优化的细菌觅食优化算法[J].控制工程,2012,19(6):993-996.
[12]KIM D H,ABRAHAM A,CHO J H.A hybrid genetic algorithm and bacterial foraging approach for global optimization[J].Information Sciences,2007,177(18):3918-3937.
[13]姜建国,周佳薇,郑迎春,等.一种双菌群细菌觅食优化算法[J].深圳大学学报(理工版),2014,31(1):43-51.
[14]湛锋,魏星,郭建全,等.基于改进粒子群优化算法的PID参数整定[J].继电器,2005,33(19):23-27.
[15]任子武,伞冶,陈俊风.改进PSO算法及在PID参数整定中应用研究[J].系统仿真学报,2006,18(10):2870-2873.
An Improved Bacterial Foraging Optimization Algorithm
LIU Zhen,SUN Jing-gao
(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)
Abstract:Aiming at the shortcomings in bacterial foraging optimization algorithm,e.g.,slower convergence speed,lower precision,easily falling into the local optimal solution,this paper proposes an improved bacterial foraging optimization algorithm.The fixed step adjusting is replaced by an adaptive step adjusting strategy via decreasing nonlinearly.By means of the idea of artificial bee colony,a mixed updating method on the bacterial position is introduced.The fittest selection criterion is improved and the crossover operator is introduced into the reproduced parents while retaining the best individual.The population evolution factor is proposed in order to prevent the stop of the evolution.Finally,the proposed algorithm is tested on the classic functions and the tuning of PID parameters,which shows their effectiveness.
Key words:bacterial foraging optimization algorithm; adaptive step;position update mode; crossover operator; population evolution factor
收稿日期:2015-03-19
作者简介:刘珍(1989-),女,山东人,硕士生,研究方向为细菌觅食优化算法与控制理论。E-mail:liuzhen10704@163.com 通信联系人:孙京诰,E-mail:sunjinggao@126.com
文章编号:1006-3080(2016)02-0225-08
DOI:10.14135/j.cnki.1006-3080.2016.02.012
中图分类号:TP273
文献标志码:A
