基于投影的组合判别方法

梁飞豹,陈婷婷

(福州大学数学与计算机科学学院,福建福州350108)

基于投影的组合判别方法

梁飞豹*,陈婷婷

(福州大学数学与计算机科学学院,福建福州350108)

摘要：由于数据的复杂性,一般的投影判别方法在应用上有一定的局限性,本文引入权重因子对不同投影方法进行组合,从而提出一种组合判别方法,以提高判别回代正确率与预测效果．通过实际例子和模拟数据验证了组合判别模型的判别效果良好,回代正确率比单一判别方法高,预测效果也优于单一判别方法．

关键词：Fisher判别;内聚外散;回代；正确率;权重;组合判别

判别分析是一种判断个体所属类别的统计方法,在已知观测对象的分类结果和若干表明观测对象特征的变量值的情况下,建立一定的判别准则,利用判别准则对新的观测对象的所属类别进行判断．判别分析方法多样,思路不尽相同,常见的判别法有距离判别分析法、最大后验概率准则、Fisher判别分析法和Bayes判别分析法等．由于数据类型的复杂性,距离判别并不能很好地体现数据所在总体潜在的几何特性．Fisher判别的决定因素是样本中心,隐含了数据是高斯分布的假设,当数据不是高斯分布时,经过任何的投影变换,都无法使其各类的组内差小、组间差大,造成各类数据分辨不清,判别效果不好．目前,并没有一种判别方法能够适用于所有的数据类型．

我们知道在预测模型中,由于建模机制和出发点不同,通常同一问题有不同的预测方法,不同的预测方法提供不同的有用信息,其预测精度往往也是不同的．如果简单地将预测误差较大的一些方法舍弃,将会丢失一些有用的信息,那么,一种更为科学的做法就是将一些不同的预测方法进行适当的组合,从而形成所谓的组合预测方法,它将有利于综合各种方法提供有用的信息,有利于提高预测的精度[1]．

在判别中,可以考虑引入组合的思想,较大限度地综合利用各种判别方法所提供的信息,尽可能地提高回代正确率．它比单个预测模型考虑问题更系统、更全面、更科学,更能有效地减少单个判别模型判断过程中一些环境因素的影响．

对于新的测试样本所属类别的判断,不同的判别方法有着不同的回代正确率和预测精度,本文尝试引入权重因子,将多种判别方法进行线性组合,构造一种组合判别方法,经过数据模拟,验证其广泛适应性,且对复杂数据判别问题有实际应用价值,理论和方法上也具有一定的创新性．

由于Fisher判别通过投影将多维的特征降到只有一维,又保证了类别能够“清晰”地反映在低维数据上．因此,本文考虑将基于投影变换的几种判别方法进行组合,既能保留投影判别的优良性,又能考虑到单个投影方向无法判别的数据经过多种判别得到较准确的结果．

1基于投影的判别方法

本文主要分析两个总体的情况,多总体的判别问题可以转换成双总体的判别分析．现考虑有n个来自总体G1，G2的p维样本

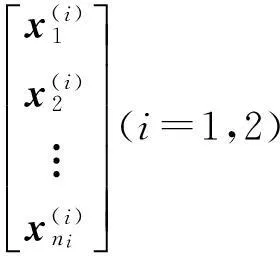
其中ni(i=1,2)表示第i个总体的样本数,n=n1+n2．在介绍投影方法之前,先定义几个必要的基本参量．

样本组间离差阵:

样本组内离差阵:

总体G2“相对于”总体G1的离差阵:

总体G1的离差阵:

总体G2的离差阵:

1)Fisher投影

将p维空间上的点x经投影后变为一维实数上的点z,并希望投影后的数据其组内差尽量小,组间差尽量大,即所求投影向量w1为:

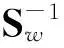
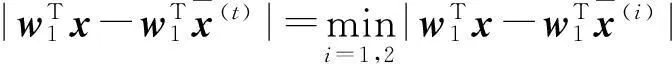
则判断样品x∈Gt．

2) 改进的Fisher投影

同样作投影,将p维投影到一维,但我们只希望投影后的数据的组间差尽量大,而不考虑组内差(这主要是为了避免p维空间上样本矩阵的组内离差阵Sw奇异),即所求的投影向量w2为:

显然w2是Sb的最大的特征值所对应的特征向量．由此投影的判别准则与Fisher投影的判别准则一致,即对于给定的任一样品x,如果

则判断样品x∈Gt．

3) “内聚外散”投影[2]

同样,将p维投影到一维,我们希望投影后的数据,属于第1类G1的样本聚集在一起,而不属于第1类G2的样本远离第1类G1(即“内聚外散”投影),即所求的投影向量w3为:

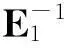
4) 改进的“内聚外散”投影

思想同上,还是希望投影后的数据,属于第1类G1的样本聚集在一块,而不属于第1类G2的样本尽可以地分散,即所求的投影向量w4为:

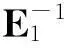
基于不同投影得到的判别方法是适用于不同的数据类型．Fisher投影判别在处理2个总体的样本数据均为高斯分布的时,效果好．而当2个总体的样本数据呈现一个集中,另一个相对分散时,“内聚外散”投影则具有更明显的优点．因此,可以说并没有一种能够适用于所有的数据类型的判别方法,下面我们将寻找一种组合方式,使得能够较好地适用于不同的数据类型做判别．

2组合判别模型

本文建立的组合判别模型拟将4种投影判别方法所得到的回代正确率作为权重,进行加权的判别方法:例如,设对某一待判样品x,2个总体G1,G2利用4个判别方法得到4个模型的回代正确率值分别为ρt(t=1,2,3,4),利用这些回代正确率值构成一个对x的最终判别结果,即x所属的类别k=φ(ρ1,ρ2,ρ3,ρ4),这种组合判别方法建立在对各个方向投影的基础上,它集多种单一判别模型所包含的信息,进行最优组合．因此,在大多数情况下,通过组合判别可以达到提高回代正确率的目的．

值得注意的是,高维的样本数据经过不同的投影降到一维后,并不能直接加权组合,而是需要处理成具有统一的标准后才能进行组合．我们采取的处理方式是:将总体G1经投影后重心(均值)落在“0”处,而总体G2的重心落在了“1”处．

组合判别方法的算法如下:

1) 选取一类样本为指定的“第1类G1”,以2个总体样本方差(取方差矩阵的行列式)大小来衡量它们的“集中”度,哪个方差行列式越小,就选择这一类为“第1类G1”;

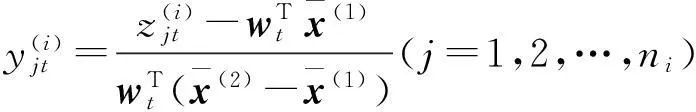
即将投影后的G1的重心落在“0”处,G2的重心落在“1”处;

4) 建立组合判别模型:

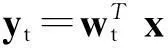
如果b=0,则判断样品x∈G1,否则x∈G2.

3数据分析

3.1实例分析

对全国30个省市自治区1994年影响各地区经济增长差异的制度变量[3]:经济增长率(%)x1、非国有化水平(%)x2、开放度(%)x3、市场化程度(%)x4．第1组的样本方差矩阵行列式D1=5.884 5×106,第2组的样本方差矩阵行列式D2=1.321 4×108,故第1组样本确定为“第1类G1”,第2组样本确定为“第2类G2”．

可以得到4个投影方向:

w1=(0.000 5-0.291 2-0.347 7-0.891 2)T,

w2=(-0.016 30.738 50.471 80.481 4)T,

w3=(0.958 8-0.265 2-0.036 60.095 5)T,

w4=(-0.959 60.257 20.036 6-0.108 2)T.

将2组样本分别向w1,w2,w3,w4上投影,并对投影后的数据进行“对折”和重心“移动”处理,得到4组一维向量如表1所示．同时我们可以得到4个投影判别的回代正确率分别是:

ρ1=0.814 8,ρ2=0.777 8,

ρ3=0.555 6,ρ4=0.592 6,

建立组合判别模型:

C=0.814 8y1+0.777 8y2+0.555 6y3+

0.592 6y4，

易得,组合判别后的回代正确率为ρC=0.851 9．

表1　4个方向投影后的数据

从回代正确率的角度看,2个“内聚外散”投影判别效果不佳,Fisher判别和改进的Fisher判别效果较好,但经过组合判别后,回代正确率得到了提高,说明该方法较单一的判别方法效果好．

3.2模拟分析

本文通过模拟数据实验来验证组合判别模型的可行性并分析其优良性．首先,构造来自2个类别的随机数据X=(X1,X2,X3,X4,X5)～Np(0,Σ),且Σ=(σij)p×p,σij=0.5|i-j|(i,j=1,2,…,p)．对于每次生成的一组样本量n=400的数据,建立模型:

Y为n×1,对Y作如下变换:

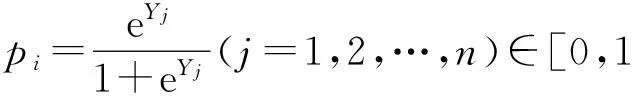
以pi为概率,自动生成一次伯努利实验,所得的值作为该样品的属类(即取值为0,作为第1类,取值为1,作为第2类),由此,可以把X分成X(1),X(2)．将X(1),X(2)各自前1/2的样本作为训练样本,剩余的部分做测试样本．

对此作大量的随机实验,组合判别均表现优良．表2随机给出了其中5次模拟实验的训练样本的回代正确率与测试样本的平均判对率．

由表2数据可知,组合判别方法充分表现出它的优良性．1)拟合度高,每次实验的回代正确率都相对较高;2)预测效果好,每次实验的预测数据的正确率也是相对较高的;3)稳定性好,每次实验的误判率都处于低水平,且波动较小．

4结论

与单一的判别模型相比,引入权重的组合判别法提高了判别的回代正确率与预测精度,而且得到的判别模型也更加稳定．

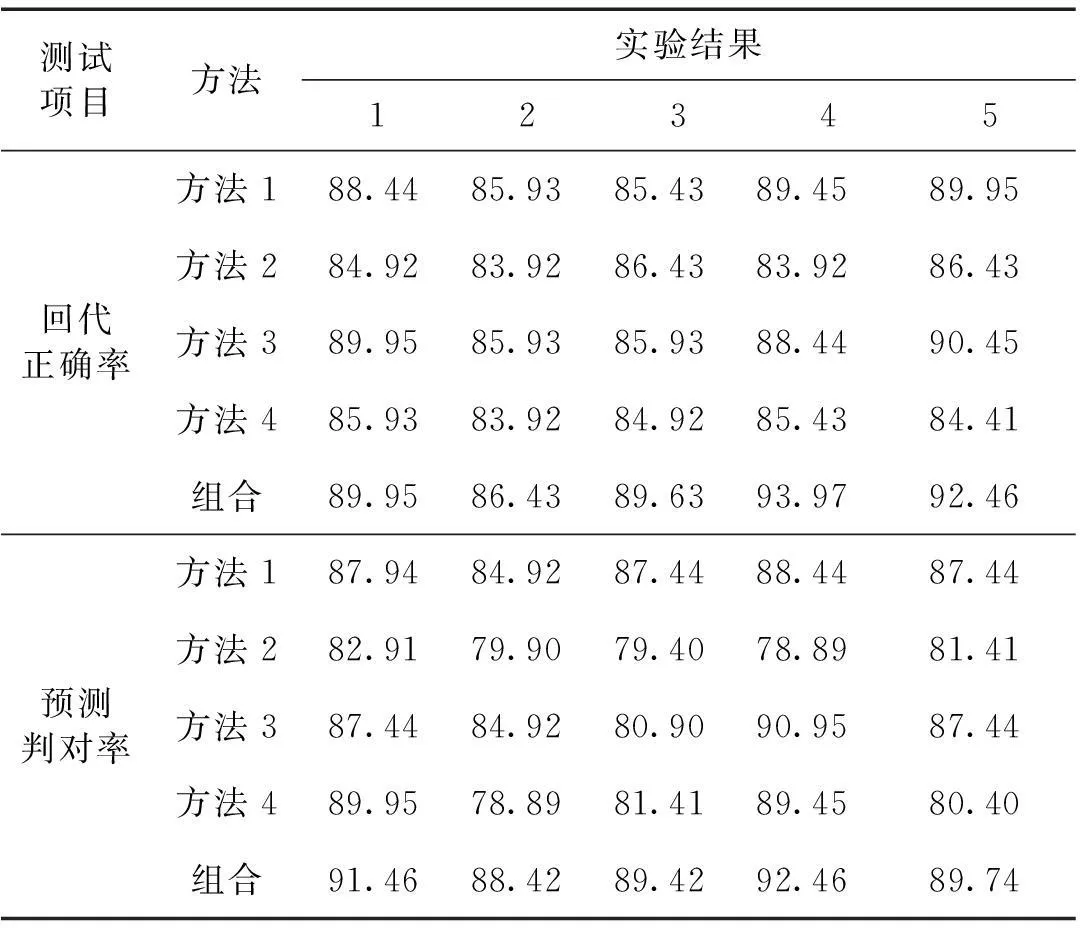
表2　模拟数据判别结果比较

注：方法1为Fisher投影,方法2为改进的Fisher,方法3为 “内聚外散”,方法4为改进的“内聚外散”.

但本文提出的组合判别方法存在待改进的地方．首先,本文只用了2种投影及其简单的推广;其次,权重的确定为回代正确率,是否还可以选择其他权重;最后,本文为今后研究提供了一个新思路,如选择其他判别方法的组合、采用非线性的组合方式等．

参考文献：

[1]石云霞．组合预测模型的权重研究及其应用[D].银川:宁夏大学,2008：2-12.

[2]梁飞豹．多次线性判别方法[J]．福州大学学报 (自然科学版),1992(1):9-15.

[3]任雪松,于秀林．多元统计分析[M]．北京:中国统计出版社,2011:15-129.

[4]游华,郭福星．最优组合因子Fisher判别法[J]．福州大学学报(自然科学版),2001,29(3):1-4.

[5]黄国宏,刘刚．一种新的基于Fisher准则的线性特征提取方法[J]．计算机技术与发展,2008,18(5):227-230.

[6]周舒冬,李丽霞,郜艳晖,等．加权Fisher线性判别法在非平衡医学数据集中的应用[J]．数理医药学杂志,2009,22:59-61.

[7]黄利文,梁飞豹．改进的Fisher判别方法[J]．福州大学学报(自然科学版),2006,34(4):473-477.

[8]苗春玉．线性判别分析改进算法的分析与研究[D]．大连:辽宁师范大学,2012：5-10.

[9]赵丽娜．Fisher判别法的研究及应用[D]．哈尔滨:东北林业大学,2013：24-26.

[10]ZHANGB,QIAOY．Facerecognitionbasedongradientgaborfeatureandefficientkernelfisheranalysis[J]．NeuralComputing&Applications,2010,19(4):617-623.

[11]MARTINEZAM,KAKAC．PCAversusLDA[J]．IEEETransactionsonPatternAnalysis&MachineIntelligence,2001,23(2):228-233.

Based on Projection of the Combination Discriminant Method

LIANG Feibao*,CHEN Tingting

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)

Abstract:Because of the complexity of the data,the general projection discriminant method suffers from certain limitations in applications．For the purpose of taking correct rates of back substitution as the standard,this article gives a combination discriminant method by introducing weighting factors and combining different projection in order to improve accuracy and prediction effects.Simulated data are checked,and it is found that their correct rates of back substitution are better than those of the general linear discriminate method．The prediction effect is superior to other methods.

Key words:fisher discriminant;assembling inside and spreading;back substitution;correct rates；weighting;combination discriminant

doi：10.6043/j.issn.0438-0479.2016.03.011

收稿日期：2015-07-09录用日期：2015-11-28

基金项目：国家自然科学基金(11301084)；福建省自然科学基金(2014J01010)

*通信作者：fbliang@163.com

中图分类号:O 212

文献标志码：A

文章编号：0438-0479(2016)03-0366-05

引文格式：梁飞豹,陈婷婷.基于投影的组合判别方法.厦门大学学报(自然科学版)，2016,55(3)：366-370.

Citation：LIANG F B,CHEN T T．Based on projection of the combination discriminant method.Journal of Xiamen University(Natural Science)，2016,55(3)：366-370．(in Chinese)